基于预训练交互式图神经网络的多元时间序列异常检测

王春枝，邢绍文，高榕，严灵毓

（湖北工业大学 计算机学院，武汉 430072）

异常检测是数据挖掘领域的一个活跃的研究课题，其广泛被用于监控工业、制造业系统和信息技术系统等系统中各个传感器的状态.从时间数据中高效且准确地识别异常值有助于持续监测传感器系统，并对潜在的事件提供及时警报.

多元时间序列是由同一实体的多个单变量时间序列组成，其中每个单变量时间序列代表系统中一个传感器的监测值.在传统研究中，异常是由相关领域的专家根据单个变量指标的特征建立相应的阈值来检测的.随着系统和数据的规模和复杂性的急剧增加，One-Class SVM［1］、K-Nearest Neighbors［2］、K-Means［3］等机器学习算法被用于单元时间序列异常检测.然而，在一个真实的复杂系统中，一个指标的变化会引起其他指标的波动.因此，单变量检测算法在多元时间序列异常检测任务中不能拥有令人满意的表现.

随着深度学习的快速发展，基于深度学习的多变量时间序列异常检测算法得到了巨大的改进.文献［4］首次研究用于检测时间序列异常的无监督深度学习方法，其采用深度卷积神经网络来检测异常.文献［5］采用的是一个基于重构的策略，其主要思想是学习一个多元时间序列的稳健表示，以重构概率来检测和解释异常.近几年，图神经网络因其结构优势在传感器间的固有关系（即特征维度的依赖关系）建模中大放异彩.文献［6］将结构学习方法与图形神经网络相结合用于捕获传感器之间的相关性.文献［7］基于图注意力网络分别对特征依赖性和时间依赖性建模，捕获到多个特征之间的因果关系以及时间维度的依赖关系，使异常检测得到进一步提升.

上述研究工作在一定程度下推动了多元时间序列的异常检测工作的进展，但是仍存在以下挑战：

（1）由于异常数据只占整体的小部分，在现有的基于预测的多元时间序列异常检测方法中，根据通常基于预测的异常检测的规定，假设训练数据仅由正常数据组成［6］.而无法忽略的是，这些异常数据仍然会增加训练数据的不可预测性.因此，本文期望的模型应该尽可能地忽略训练数据中的异常波动.

（2）时间序列是一种特殊类型的序列数据，它拥有着其他类型的序列数据不具备的特征：趋势性、季节性，合理的利用这两个特征可以协助我们进行正常的预测.现有的深度学习技术使用通用序列模型进行时间相关性建模，而忽略了它的独特特性.

为了应对多元时间序列异常检测中的上述挑战，本文提出了一种基于预训练交互式图神经网络（PT-IGNN）.具体而言，PT-IGNN由预训练模块、预测模块组成.其中，预训练模块利用无标签数据，基于Transformer［8］编码器进行多元时间序列的表示学习，其目的是削弱训练数据中的异常波动带来的影响.预测模块通过GATv2［9］尝试显式地建模不同传感器之间的相关性，同时对每个时间序列内的时间依赖性进行建模.为了更好地利用时间序列独特的特性，本文基于时间卷积构建了一个交互式的树状结构，不仅实现了更大的感受野，而且避免了TCN［10］只能从上一层的特征中提取时间动态的能力限制.树状结构的天然优势可以将上层的信息将逐渐累积向下传播，从长期和短期的依赖中学习隐藏的时间依赖关系，促进了对时间序列的预测能力.

本文的主要贡献总结如下：

（1）提出了一个多元时间序列的预训练方案.通过基于改进的Transformer编码器学习时序数据密集向量表示，削弱训练数据中的异常波动带来的消极影响.

（2）基于时间序列的独特特征，提出了一种交互式的树状结构，通过在不同时间分辨率下迭代提取和交换信息，可以学习到具有较高可预测性的有效表示.

（3）在来自工业领域的3个真实多元时间序列数据集上进行的大量实验表明，本文的模型始终优于最先进方法.

1 PT-IGNN算法的设计

1.1 问题阐述

多元时间序列异常检测旨在检测实体层面的异常［5］.在本文中，多元时间序列异常检测的输入序列由传感器随时间变化的传感器数据组成X={x1，x2，…，xn}∈Rn×m，其中n是时间序列的长度，m是产生多元时间序列的传感器的数量.

由于时间序列数据量比较庞大，本文每次迭代时只取t时刻前w个时间戳的数据{xt-w，xt-w+1，…，xt-1}∈Rw×m预测t时刻的值，预测结果定义为x^t.本文的目标是对测试集中的异常数据进行检测，将真实值xt与预测值x^t的偏差看作异常分数，异常分数越大，表示t时刻发生异常的可能性越大，如果异常分数超过特定的阈值，则判定t时刻发生了异常.

1.2 整体架构

针对现有基于预测算法的不足：1）. 训练集中的异常数据会增加模型的不可预测性；2）. 忽略了多元时间序列中独特特性.本文所提出的PT-IGNN由预训练模块和预测模块组成如图1所示.预训练模块改进Transformer的编码器以更加适合处理含有异常的时间序列数据，并且设计了一个去噪的自回归任务以提取多元时间序列的密集向量表示.本文在预测模块中提出了一个交互式图神经网络（IGNN），其由堆叠的特征-时间块和预测层组成.每个特征-时间块由一个特征块和一个时间块交错组成，以在动态变化的上下文中联合提取时间序列的特征维度和时间维度的依赖关系.特征-时间块可以进一步堆叠以获得更好的预测精度.随后，预测层利用两个1×1卷积层来聚合这些特征以进行时间序列预测.为了避免梯度消失的问题，从特征块的输入到时间块的输出添加了剩余连接，同时在每个特征块之后添加跳过连接.

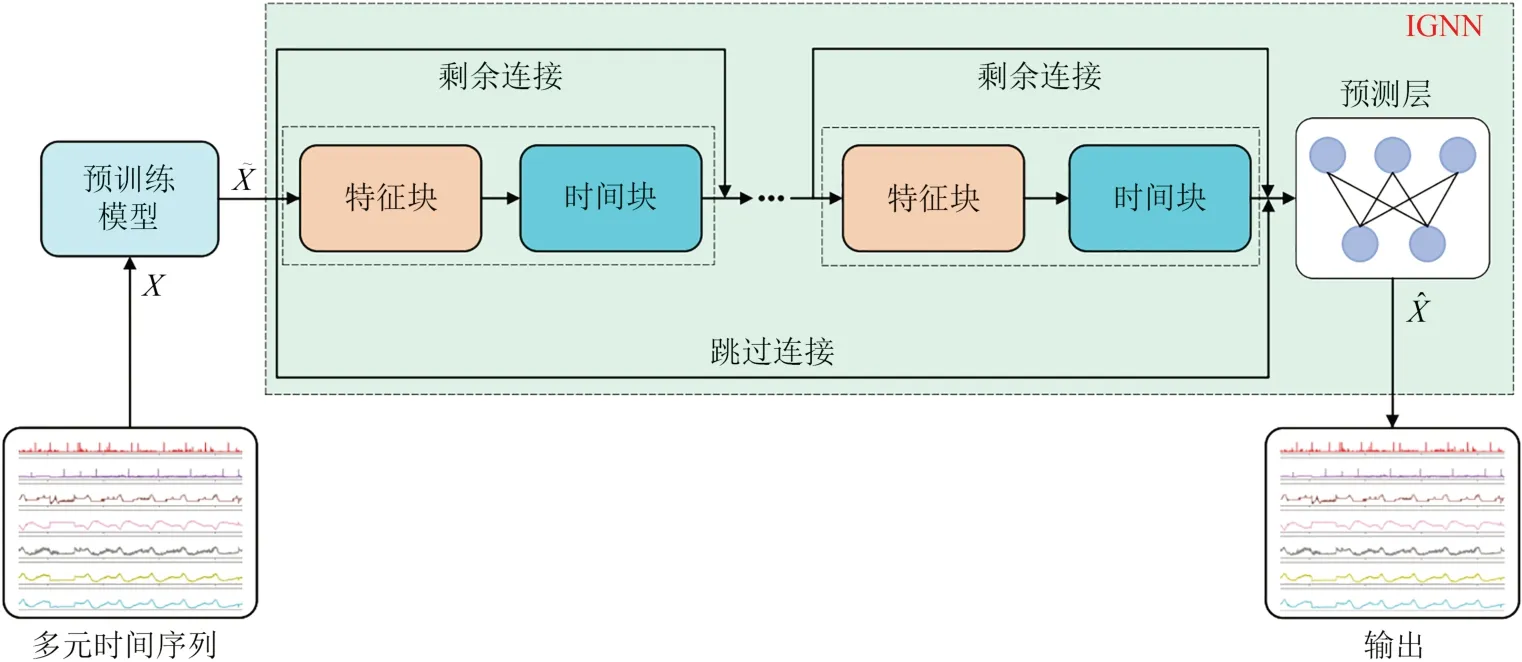
图1 PT-IGNN模型整体架构图Fig.1 The overall architecture of PT-IGNN model

1.2.1 IGNN

特征块采用GAT的修正版GATv2建模时间序列的特征依赖，GATv2实现了一个通用的近似器注意函数，更适合动态变化的时间序列任务.时间块负责学习时间序列的时间依赖性，其引入了一种交互式的树状结构，它由多个基本构建节点分层排列.每个节点将输入数据下采样为两个子序列，然后使用不同的卷积模块提取每个子序列的特征并加入交互学习补偿下采样过程中的信息损失.

预测层由两个经典的卷积层构成，根据最后一个特征-时间块的融合特征进行时间序列预测.本文使用预测输出和观测数据之间的均方误差作为最小化损失函数.

1.3 预训练模块

1.3.1 改进的Transformer

考虑到模块的通用性，本文只使用Transformer编码器.Transformer最初是为自然语言翻译任务提出的强大模型，与离散词索引的序列更加兼容.为了更适用多元时间序列异常检测任务，在此提出以下建议的变化如图2所示，更多对Transformer模型的详细描述请参考原始工作［8］.

图2 预训练模块所使用的Transformer编码器Fig.2 Transformer encoder used by the pre-training module

自然语言处理（NLP）中使用Layer Normalization可以取得比使用Batch Normalization明显的性能提升［8］，因为词嵌入中不会受离群值带来的影响.然而多元时间序列异常检测的训练数据中是存在离群值的.此外，NLP中批量归一化的性能较差，主要归因于样本长度的极端变化，而在我们考察的数据集中，这种变化要小得多.故本文使用Batch Normalization来代替Layer Normalization，因为它可以减轻时间序列中离群值的影响，同时我们观察到Batch Normalization在所有实验中表现得更加令人满意.

Transformer中使用注意力取代了循环神经网络，导致了位置信息的缺失，模型对输入的顺序不敏感，为了使它意识到时间序列的顺序性，需要将位置编码Wpos∈Rw×d添加到输入向量中.相比于原工作中提出的确定性的正弦编码，本文使用了可学习的位置编码，随着模型一起训练学习.可学习的位置编码在所有的数据集中有着更加突出的表现，本文推测它们在学习的过程中被投影到高维子空间中，其与时间序列样本所在的子空间不同且呈现出近似正交的关系.

Transformer的成功很大程度上得益于self-attention机制，但是其每层的时间复杂度和内存使用量达到O(n2)的计算复杂度，为实际应用带来负担.文献［11］提出的ProbSparse自注意力机制在时间复杂度和空间复杂度方面实现了O(n·logn)，并在序列依赖对齐方面具有相当的性能.在本文中，本文引用ProbSparse自注意力来加速预训练模块的计算速度.

1.3.2 预训练

受BERT［12］启发，本文对训练数据设计了一个无监督的去噪自回归任务，鼓励模型学习变量之间的相互依赖关系，降低训练数据中的异常数据带来的影响.具体来说，本文为每次训练的时间序列X生成一个二进制噪声掩码M∈Rw×m，通过元素乘法屏蔽部分输入数据Rw×m，并要求模型预测被屏蔽的值.整个过程直接从时间序列数据中学习，不借助于任何标签以及先验信息.

正常的时间序列数据中很少会出现突然的变化，如果数据中遮蔽序列的长度非常短，那么则可以通过复制前后的值或取区域平均值来很近似地预测.所以本文希望能够控制遮蔽序列的长度，而不是简单地使用某种分布来独立地随机设置噪声掩码.本文定义掩盖的比例为r，即在每个时间步长内，平均r·m个变量的值将设置为0.本文使每个长度为w序列为0的掩码段的长度遵循平均数为lα的几何分布，未掩码段的平均长度为在本文中，因为数据含有异常段，一个非常高的掩盖比例r会使模型无法收敛，最终本文根据大量实验结果选择了r= 0.1，并在所有的实验中选择lα=3.这种输入掩蔽模式鼓励模型关注单个特征的前后片段，以及时间序列中其他变量的当代值，从而对变量之间的相关性进行建模，再结合时间维度的相关性来平滑训练数据中的差异.

其中Wu∈Rd×m，bu∈Rd随着模型一起学习，ut∈Rdfort∈{0，…，w}是预训练模块的输入向量，然后加上位置编码并乘以相应的矩阵后作为self-attention层的查询、键和值.最后将编码器的输出向量zt∈Rd馈送到一个线性层中以对输入向量进行完整地预测.为了学习模型的参数，本文使用均方误差作为损失函数.

值得注意的是，本文只计算每个数据样本中被屏蔽部分的预测值和实际值的误差，这与其他预训练模型［12-13］是一致的.

1.4 预测模块

预训练模块提取多元时间序列的密集向量表示，在本节中，本文设计了一个交互式图神经网络用于多元时间序列预测，其从特征维度和时间维度出发，分别学习多元时间序列的特征间依赖关系和时间依赖关系.

1.4.1 特征块

从基于图的角度，本文将每个传感器看作图中的单个节点.在大多数情况下，多元时间序列并没有提供明确的有关图形结构的先验信息，本文引入一个被随机初始化的传感器嵌入向量V={v1，…，vm}∈Rm×dv，其中vi∈Rdv表示传感器i的特性，随模型的其余部分一起训练.实际场景中，如果两个传感器的行为类似，那么两个传感器的行为也类似.理想情况下，经过学习后的嵌入向量可以很好地表示传感器的行为特性，故本文将这些嵌入用于计算传感器之间行为的相似度φ，并在传感器i与相似度最大的前k个候选传感器之间建立有向边.

其中j∈{1，2，…，m}∖{i}表示传感器i可以依赖的候选传感器.

GAT是用图进行表示学习的最先进的体系结构之一.在GAT中，每个节点通过处理它的邻居能够对任意图中节点之间的关系进行建模.然而，GAT中的注意机制是一种受限的静态注意力：对于任何查询，它的邻居节点的评分对于其他节点的分数都是单调的，即注意力分数的排名是不以查询节点为条件的［9］.在此基础上，GATv2模型提出了一种比GAT更具表现力的动态图注意力变体，即注意力分数会随着查询节点的不同而变化.两者主要的形式区别在于计算注意力的公式有所改变.

一般来说，给定一个有n个节点的图，输入的是一组节点表示{hi∈Rd|i∈{1，…，n}}，GAT利用评分函数e对节点对进行打分，从而避免一些GNN架构中邻居权重一致的问题.

其中a∈R2d′，W∈Rd×d′是可学习的，⊕表示表示两个节点表示的连接.节点i与所有的邻居节点计算分值之后，利用softmax进行归一化：

其中L表示节点i的相邻节点数.GAT计算每个节点的输出表示如下：

GATv2指出标准的GAT的问题在于scoring function，其中的a，W是依次被用于运算的，它们很可能会坍缩成一层的线性层.为了解决这个问题，GATv2修改了注意力中线性变换的计算顺序，得到了更具表达力的注意力，具体改变如下：

考虑到现实中传感器间的依赖关系是复杂多变的，特征之间包含更复杂的交互，故本文使用GATv2来建模传感器间的依赖关系，消融实验也证明了GATv2拥有更出色的表现.

1.4.2 时间块

时间序列是一种特殊的序列数据，为了更好的利用它的特性，本文将多个T-Node节点排列成一颗深度为h的满二叉树结构如图3（a）所示，即在第h层有2h-1个T-Node节点.通过不同的层级逐渐下采样处理，更深层级的特征将包含来自较浅层次的更精细尺度的时间信息.通过这种方式可以捕获不同时间尺度下的长短期时间依赖关系，从而降低异常数据的影响，增强原始多元时间序列的可预测性.

图3 时间块整体架构图Fig.3 Temporal block overall architecture diagram

T-Node节点主要由分裂和交互学习两个部分构成如图3（b）所示.首先根据下标的奇偶性将原始序列下采样为两个子序列，这两个子序列具有比原始序列更大的时间尺度，但保留了大部分信息.为了从每个子序列中提取同构和异构信息，本文设计了由两个一维卷积层构成简单的模块，然后通过交互学习的策略补偿下采样过程中的信息损失.

具体而言，首先将输入向量根据下标奇偶性划分为两个子序列两个子序列之间的信息交流是通过对仿射变换参数的相互学习来实现的，交互式学习过程包括两个步骤.

第一步，在两个子序列上进行缩放变换，其缩放因子是学习得到的.首先，分别使用两个不同的一维卷积模块将变换到隐藏状态，然后通过softmax函数进行归一化操作，最后分别与和执行元素乘积.

其中，θ表示一维卷积模块，以不同的下标作为区分.⊙是Hadamard乘积.

特别地，与常用于时间序列建模的扩展卷积相比，上述的体系结构从两个下采样子序列中提取的基本信息，实现了更大的感受野.在完成上述所有的步骤之后，本文按照奇偶顺序重新组合树中所有的叶子结点，将它们串联成一个新的序列表示，最后通过残差连接添加到原始时间序列中.

综上，算法1以伪代码形式简单的说明了PTIGNN模型的训练过程.

1.5 异常评分

与预测的损失目标类似，本文将时间戳t的预测值与实际值xt之间的平方偏差作为异常分数，表示模型的预测值与真实值的偏差程度，分数越高的时间戳发生异常的可能性越大.具体来说，时间戳t的异常得分st为：

如果st超过一个固定的阈值，即认为在t时刻发生了异常.在现有工作中，很多不同的阈值的设置方法被提出，如被广泛使用的基于极值理论提出的一种自动选取阈值的方法SPOT［14］.由于同一异常检测模型在不同异常阈值下的检测性能也不同，我们在所有可能的异常阈值范围内进行网格搜索，并从中选取得到最优结果.

2 实验与分析

2.1 实验设置

本文采用文献［15］提出的点调整方法来计算模型的性能，该方法被广泛用于时间序列异常检测任务的评估［5，7，16-18］.在实践中，一个指标的异常通常会导致其他指标的异常，这将在一段时间内形成来连续的异常段.任何一个异常窗口所包含的时间戳触发异常报警都是可以接受的.更具体地说，如果检测到测试集中某一异常段的任何异常，则认为该段的所有异常都可以通过该阈值检测出来，而异常段以外的点则不做额外处理.

2.1.1 数据集

本文在广泛的收集自现实世界的真实异常检测数据集上评估文中的方法.MSL和SMAP是由NASA收集并发布的航天器数据集［19］，每个数据集都有一个训练子集和一个测试子集，两个测试子集都有标签文件，其中标记了所有的异常.SMD［5］是一个应用服务器数据集，是目前用于评估多元时间序列异常检测的最大的公共数据集.它包含28个不同服务器，每个服务器有38个特征，代表服务器不同的指标（CPU负载、网络使用等指标），其中前一半的数据用于训练，另一半的数据作为测试集（表1）.

表1 数据集的统计信息Tab.1 Statistics of the data set

2.1.2 评价指标

本文使用主流的异常检测评价指标Precision（P）、Recall （R）、F1-Score （F1）来评估各个模型的性能，三个指标的值越高，表明模型性能越强：

其中TP和FP分别代表真正检测到的异常和错误检测到的异常，FN指错误分类的正常样本.

2.1.3 训练设置

本文使用PyTorch（V1.9.0与Python 3.8.10）实现了这些算法及其所有变体.所有的实验都在装有NVIDIA GeForce RTX 3080 GPU的Windows机器上运行.本文采用PyTorch Geometric library （v2.0.1）中提供的GATv2，其是原作者公开的代码.对于多元时间序列预测，在MSL、SMAP数据集是使用大小为50、80的滑动窗口，而SMD数据集的历史窗口大小为100.预训练模块中，模型维度设置为128，多头注意力的头的数量设置为8，本文使用RAdam优化器以初始学习率0.001对模型进行500个epoch的训练.对于预测模块，时间块中树的高度为3，本文训练模型50个批次，批次大小设置为64，初始学习率为0.0002.此外，采用早停策略和dropout策略防止过拟合，两个模块的dropout率分别为0.1、0.4.

2.2 性能比较与分析

为了验证本文提出多元时间序列异常检测算法的有效性，选取如下的典型检测算法作为对比方法：LSTM-NDT［20］、LSTM-VAE［21］、OmniAnomaly［5］、MAD-GAN［22］、GDN［6］、MTAD-GAT［7］、GReLeN［23］.MTAD-GAT、GReLeN均是非常优秀的模型如表2所示，分别在不同数据集上表现出次优的性能.本文的模型具有更加出色的泛化能力，在所有数据集上一致获得了最佳F1成绩，这是其他基线无法比拟的.具体来说，我们在MSL、SMAP和SMD数据集上，与最先进的性能相比，分别取得了2.0%、1.5%和0.8%的性能提升.从表2中，我们可以得出以下观察结果：

表2 不同模型的性能比较Tab.2 Comparison of performance of different models

（1） LSTM-NDT在MSL与SMD数据集上表现最差，而LSTM-VAE在SMAP数据集上表现最差.这是合理的，因为LSTM-NDT仅仅考虑了单变量时间序列的时间模式，忽略了传感器间的依赖关系，这导致其在含有大量传感器时无法进行准确的预测.LSTM-VAE将LSTM和VAE进行简单地结合，同样也只对时间依赖关系进行建模，然而，它的性能在两个数据集上明显优于LSTM-NDT模型，这可能是因为LSTM-VAE是一个基于重构的模型，相对于基于预测的模型对时间序列短期的数据变化规律具有更好的捕捉能力.

（2）相反，OmniAnomaly通过随机方法建模传感器间的依赖关系，MAD-GAN利用对抗训练学习传感器间的依赖关系，均取得较好的性能.然而它们都忽略了时间维度的低维表示，在时间依赖性建模方面表现不好.这两种方法都是基于重构的模型，在训练学习的过程中，它们会尽可能好的重构窗口内的数据，而实际上，训练数据是含有异常数据的.

（3）与上述不同的是，GDN、MTAD-GAT以及GReLeN都是基于图学习的异常检测方法.GDN未考虑时间序列的时间依赖，这大大影响了其模型的表现能力.MTAD-GAT联合了基于预测和基于重构的模型，使用图注意力网络分别学习时间维度和特征维度的依赖关系.但是，它假设数据集中的所有传感器都是相互依赖的，这不仅忽略了传感器之间复杂的部分方向依赖关系，而且不适合许多实际情况.GReLeN着重于学习传感器之间的潜在依赖关系，通过将变分自动编码器与图神经网络巧妙地结合，在两个数据集上取得了次优的性能.

本文的模型首先通过预训练提取多元时间序列的密集向量表示，降低训练数据中异常数据带来的负面影响，增强了异常时间序列的可预测性.本文同时考虑了时间序列的特征依赖和时间依赖，而且通过了一种交互式的树状结构利用了被其他模型忽略时间序列的独特性.综上所有因素，得以使本文的模型优于其他模型.

2.3 消融实验

为了进一步评估本文的方法中各个组件的有效性，本文设计了几组消融对比实验，以观察模型性能如何在三个数据集上下降.各个模型之间只做以下改变，其他参数均保持一致.

（1） w/o Pre-Train：移除预训练模块，将原始序列投影到一个d维的向量空间之后，直接作为IGNN的输入数据.

（2） w/o Feature：移除特征块，在IGNN中，仅学习时间序列的时间依赖关系.

（3） w/o Temporal：移除时间块，在IGNN中，仅学习时间序列的特征依赖关系.

对于预测模块，为了验证图结构学习的重要性和交互学习的有效性，本文在以下两种变体上进行了实验.

（4） w/o GATv2：将GATv2替换为GAT，用于学习传感器间的依赖关系.

（5） w/o Inter-Learn：将公式（9）～（12）替换为如下公式：

从图4可以看出，预训练模块、特征块和时间块三者缺少任何一个部分都会导致模型性能的下降.其中，w/o Pre-Train模型的表现力与上一节中各个检测方法相比并没有明显的优势，而本文完整的模型却有显著的提升，这是因为预训练模块使时间序列尽可能的“正常”，削弱了异常数据给下游预测任务带来的不利影响.w/o Feature模型导致性能下降程度最大，在SMAP数据集上尤为明显，F1分数较完整模型下降了10.65%.这表明学习特征间依赖关系可以提高了模型的性能，特别是对于特征数目较多数据集.w/o Temporal模型不考虑时间序列的时间依赖关系，也使模型性能大幅下降.w/o GATv2很好地说明了GATv2在处理多元时间序列异常检测中的优越性.w/o Inter-Learn也证明了时间块中设计的交互式学习是至关重要的，它可以提高各个数据集的检测精度.

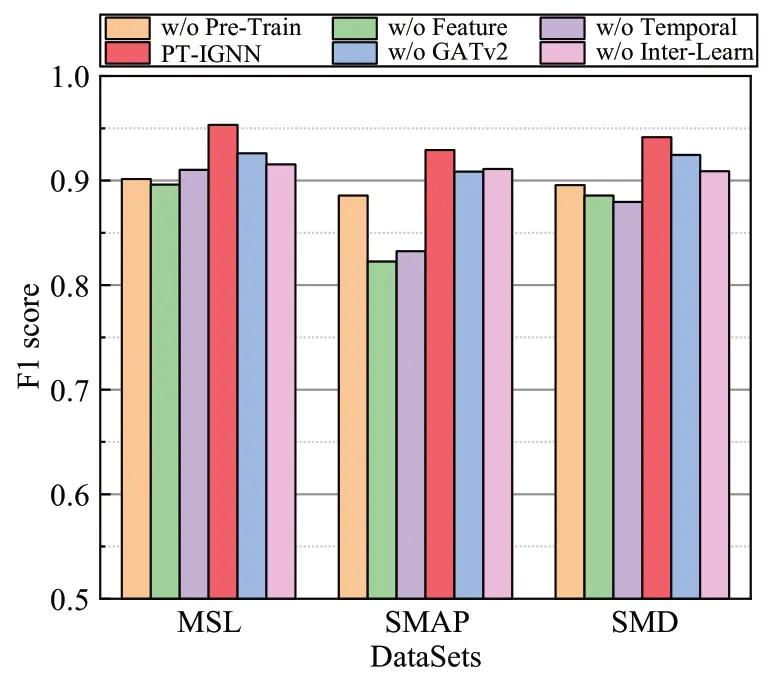
图4 PT-IGNN和其变体的F1分数Fig.4 F1-score of PT-IGNN and the variants

直观地说，时间序列异常检测必须综合考虑其特征间依赖关系和时间依赖关系，才能够更好的对时间序列做出更符合正常规律的预测，从而在异常时刻得出较大的异常得分.同时，我们也可以通过别的方式来促使模型去关注正常数据的规律，比如本文所使用的预训练方式.这些实验表明，移除PTIGNN模型中的任何一个组件，都会导致性能的下降，而综合考虑全部组件，模型将会达到最佳性能.

2.4 异常解释

在实践中，多元时间序列中的异常现象的发生是多个传感器综合作用的结果.异常解释是异常检测中的一个重要部分，它可以帮助操作者理解和处理异常情况.

与top-k推荐领域内的HR指标类似，“解释分数”（IPS）指标是异常检测领域最常用的异常解释指标之一，用来评估分段级别的异常解释的准确性［17］.直观上，IPS@P%是在分段级别评估的最高命中率的加权总和.其中，GTΦ表示导致GΦ内的数据发生异常的真实原因，|GTΦ|为GTΦ中的传感器个数.

与文献［5，17，24］类似，本文仅在SMD数据集上进行异常解释实验，因为只有SMD提供了导致数据异常的真实解释标签，而且标签没有按照特定的顺序列出，所有标签具有同等的重要性.图5显示了将P从100增大到150后，每种方法对所有探测异常的平均解释精度.由于MAD-GAN未提供标准异常评分，因此不包括在比较中.对于所有的方法，IPS@P%随着P的增加而增加，因为其包含了更多的真实标签.在不考虑P的情况下，PT-IGNN的性能优于其他最先进的方法，证明了本文模型的优越性.

图5 PT-IGNN和基线的异常解释Fig.5 PT-IGNN and baseline anomaly interpretation

3 结论

多元时间序列异常检测可以极大地帮助人们及时发现和排除设备的异常行为.本文提出基于预训练的交互式图神经网络（PT-IGNN），其首先通过预训练的策略来削弱训练数据中异常数据的不利影响，使模型能够更好的学习时间序列的正常模式.然后从时间序列的特征出发，通过GATv2和一种交互式的树状结构分别学习特征间依赖和时间依赖关系.此外，基于通用模型的异常解释实验证明了PT-IGNN具有良好的异常解释能力，这可以帮助操作者在实践中快速定位异常的根源.