简谐振动的仿真与分析
高彩云
(山西大同大学物理与电子科学学院,山西大同 037009)
物体在平衡位置附近往返运动叫振动(或机械振动),物体在线性恢复力作用下围绕平衡位置的振动叫简谐振动(Simple harmonic vibration,又称简谐运动),它是一种由自身系统性质决定的周期性运动[1]。简谐振动最基本的机械振动。简谐振动的运动方程、特征量、相位与初相位、速度与加速度、能量及简谐振动的合成与分解是机械振动中的主要内容,也是大学物理课程中的重点和难点内容。近年来,随着计算机软件技术的发展,人们开始用数值计算软件来仿真模拟,常用的是Matlab软件和Origin,现有研究主要集中在波动光学实验的仿真,如牛顿环实验仿真、光栅衍射实验仿真、劈尖干涉验仿真、等倾干涉图样[2-7];也有少数关于静电场和简谐振动的仿真研究,如钱宏明等进行了一维电荷分布系统的静电场模拟[8];关于简谐振动的仿真研究,文献主要采用Matlab 软件仿真了简谐振动位移、速度等曲线合振动过程中的动能、势能以及机械能等[9-10]。使用Matlab 执行的时候是一边转换为二进制可执行代码一边运行,速度比较差,遇到字节比较多或者复杂以及精度高程序的就容易卡慢,而作为同样功能强大的数据分析和图形可视化软件,Origin 是集绘制图和数据分析为一体的理想工具,同时还具有简单易学、操作灵活、强大的数学运算功能等特点。
采用Origin 2022 软件对简谐振动的运动方程、位移、速度、加速度、能量转化和振动合成等问题进行仿真分析,以此来辅助简谐振动教学环节。
1 简谐振动的运动方程
以弹簧振子为例,设滑块的质量为m,弹簧的劲度系数为k,将振子视作质点,忽略摩擦。质点受力大小与位移成正比,而方向相反。根据牛顿第二定律得动力学方程为:
式中:ω2=,其值决定于弹簧的劲度系数和滑块的质量。式(1)根据常微分理论可解得:
式中:A和φ是待定常数,需要根据初始条件来决定。式(2)也可转换成正弦函数来表示,可见,简谐振动是围绕平衡位置的周期运动,其位移是时间t的正弦或余弦函数。
1.1 运动方程仿真
采用Orign软件将简谐振动的运动方程进行仿真,具体操作过程如下:首先打开软件新建新的空白图形窗口,设置横坐标范围(0,16),纵坐标范围(-2,2),修改横、纵坐标轴标题、刻度及水平轴的位置(-50%);然后新建2D函数图,自变量在(0,16)中取1 000个点,分别输入函数Y(x)=cos(pi/4*x)、Y(x)=2*cos(pi/4*x)、Y(x)=cos(pi/8*x)、Y(x)=cos(pi/4*x+pi/2),各运动方程的特证量如表1,位移-时间曲线如图1。
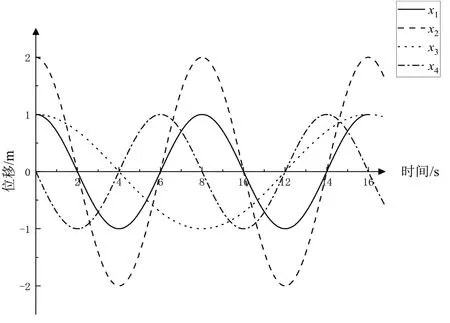
图1 不同特征量简谐振动的位移-时间曲线

表1 不同简谐振动运动方程特征量
1.2 结果分析
由图1 可见,简谐振动的位移-时间曲线呈现余弦(或正弦)规律,具有周期性。曲线的形状和在坐标轴的位置由特征量决定,其中振幅大小决定曲线的“高低”,x2的振幅为2 m,值最大,曲线最高;圆频率的大小影响曲线的“疏密”,x3的圆频率为π/8,值最小,曲线最“稀疏”;初相位则决定曲线在横轴上的位置,x1、x2、x3的初相位均为0,曲线在横轴上的位置相同,t=0 时质点处于最大位移处,x4的初相位均为π 2,t=0时质点处于平衡位置处。
2 简谐振动的位移、速度与加速度
根据简谐振动的运动学方程
对t求导数,得简谐振动的速度为:
也可表示成
再对t求导数,得简谐振动的加速度为:
也可表示成
由式(3)、(4)可知,简谐振动的速度和加速度同样是时间t的正弦或余弦函数,与运动方程具有相同的周期,但最大值不同。
2.1 Origin仿真
采用Orign软件将简谐振动的速度和加速度进行仿真,具体操作过程如下:首先打开软件新建新的空白图形窗口,设置横坐标范围(0,2π),纵坐标范围(-4,4),修改横、纵坐标轴标题、刻度及水平轴的位置(-50%);然后新建2D函数图,自变量在(0,2π)中取1000个点,分别输入函数Y(x)=cos(2*x)、Y(x)=-2*sin(2*x)、Y(x)=-4*cos(2*x),位移、速度和加速度的特征量如表2,位移、速度和加速度随时间变化曲线如图2。
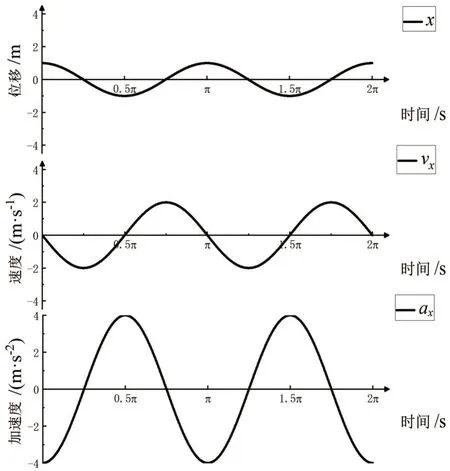
图2 位移、速度和加速度随时间变化曲线
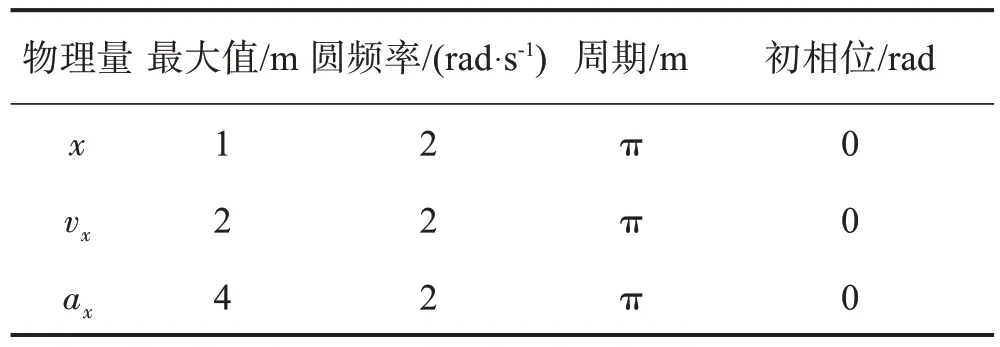
表2 位移、速度和加速度特征量
2.2 结果分析
由图2 可见,简谐振动的位移、速度和加速度都随时间呈现正弦或余弦规律变化,周期均为π,加速度的峰幅值大,变化最快。当位移达到正最大值时,质点运动到最大位移处,速度为0,加速度为负最大值,将返回到平衡位置;当位移为零时,质点运动到平衡位置处,速度达到负最大值,加速度为零;当位移达到负最大值时,质点运动到负最大位移处,速度为0,加速度为正最大值,将返回到平衡位置。
3 简谐振动的相轨迹
用质点坐标和速度建立坐标系,得到的相平面也可以描述简谐振动的状态。相平面上的任意一点代表该时刻的运动状态,质点运动状态在相平面上移动而画出的曲线即相轨迹。消去式(2)、(3)中的t,得:
将初始条件t=0,x=x0,νx=ν0x代入式(2)、(3),得:
可见,简谐振动的相轨迹是椭圆,其形状和大小取决于初始条件。
3.1 相轨迹仿真
采用Orign 软件将简谐振动的先轨迹进行仿真,具体操作过程如下:首先打开软件新建新的空白图形窗口,设置横坐标范围(-6,6),纵坐标范围(-6,6),修改横、纵坐标轴标题、刻度及水平轴和垂直轴的位置(-50%);然后新建2D 参数函数图,自变量在(0,2π)中取1 000 个点,分别输入函数X(t)=cos(t),Y(t)=sin(t);X(t)=2*cos(t),Y(t)=2*sin(t);X(t)=5*cos(t),Y(t)=3*sin(t)。不同相轨迹曲线的特证量如表3,相轨迹曲线如图3。
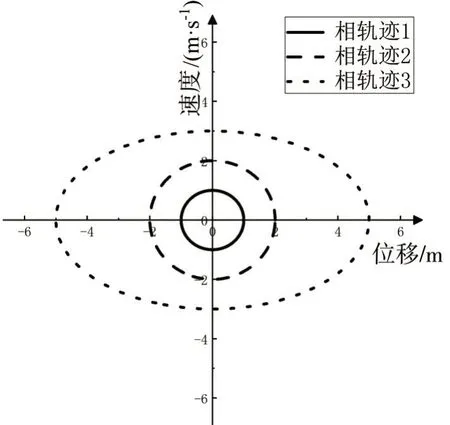
图3 不同简谐振动的相轨迹

表3 相轨迹特征量
3.2 结果分析
由图3 可见,简谐振动的相轨迹是椭圆或圆,其形状和大小由简谐振动的初始条件决定。当圆频率等于1 时,相轨迹为圆,如相轨迹1 和相轨迹2,;当圆频率不等于1 时,相轨迹为椭圆,如相轨迹3;椭圆的长半轴长度由振幅决定,即由振动的初始条件决定。
4 简谐振动的能量
以弹簧振子为例,应用质点动能公式Ek=将式(3)代入,得它在振动的过程中的动能为:
将运动方程代入势能EP=,得:
故系统总的机械能为:
4.1 能量转化仿真
设弹簧劲度系数为1 N·m-1,初相位为零,振幅为2 m。采用Orign 软件将简谐振动的动能、势能和机械能进行仿真,具体操作过程如下:首先打开软件新建新的空白图形窗口,设置横坐标范围(-2π,2π),纵坐标范围(0,2),修改横、纵坐标轴标题、刻度及垂直轴的位置(-50%);然后新建2D 函数图,自变量在(0,2π)中取1 000 个点,分别输入函数Y(x)=2*sin(x)*sin(x)、Y(x)=2*cos(x)*cos(x)、Y(x)=2。简谐振动的动能、势能及机械能随时间变化的曲线如图4。
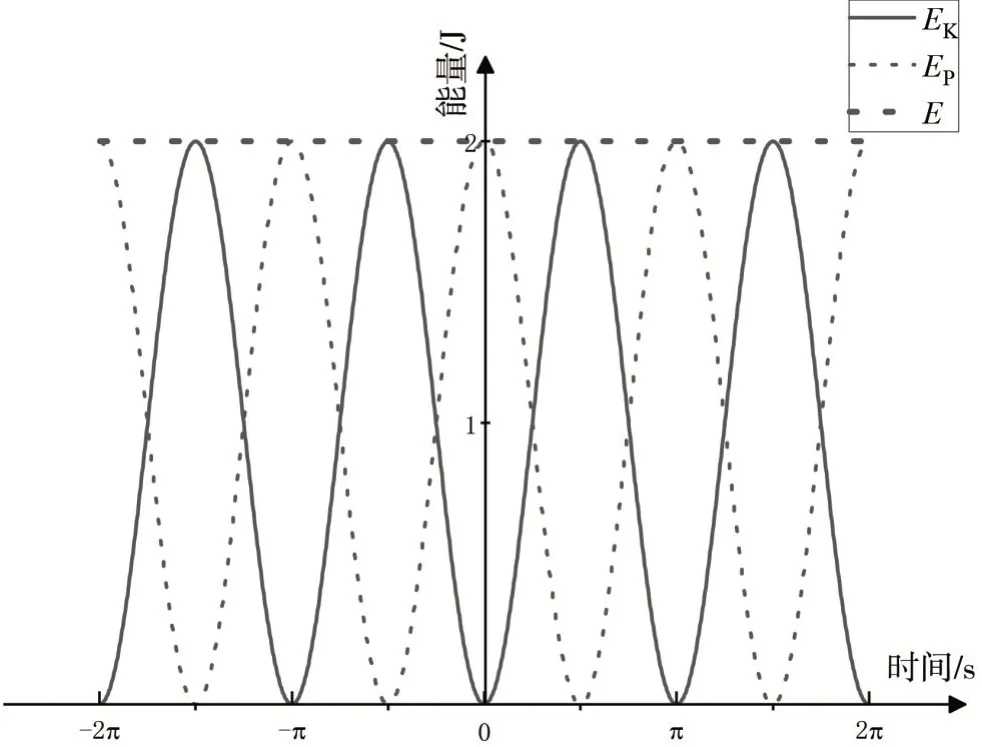
图4 简谐振动的能量随时间变化及互相转化
4.2 结果分析
由图4可见,简谐振动的动能和势能均按正弦或余弦函数的平方随时间变化。动能最大时,势能最小,动能最小是,势能最大,简谐振动的过程就是动能与势能相互转化的过程,总的能量不变,且大小取决于系统的劲度系数与振幅。
5 简谐振动的合成
若质点同时参与几个简谐振动,则其振动应为几个振动的合成,下面以两个振动合成为例,按照分振动的方向和频率的关系进行讨论分析。
5.1 Origin仿真
5.1.1 同方向同频率简谐振动的合成
采用Orign 软件将分振动和合振动进行仿真,具体操作过程如下:首先打开软件新建新的空白图形窗口,设置横坐标范围(0,8π),纵坐标范围(-3,3),修改横、纵坐标轴标题、刻度及轴的位置;然后分别新建2D 函数图,自变量在(0,8π)中取1 000 个点,输入函数Y(x)=cos(x)、Y(x)=2*cos(x)、Y(x)=3*cos(x)。振动曲线如图5。
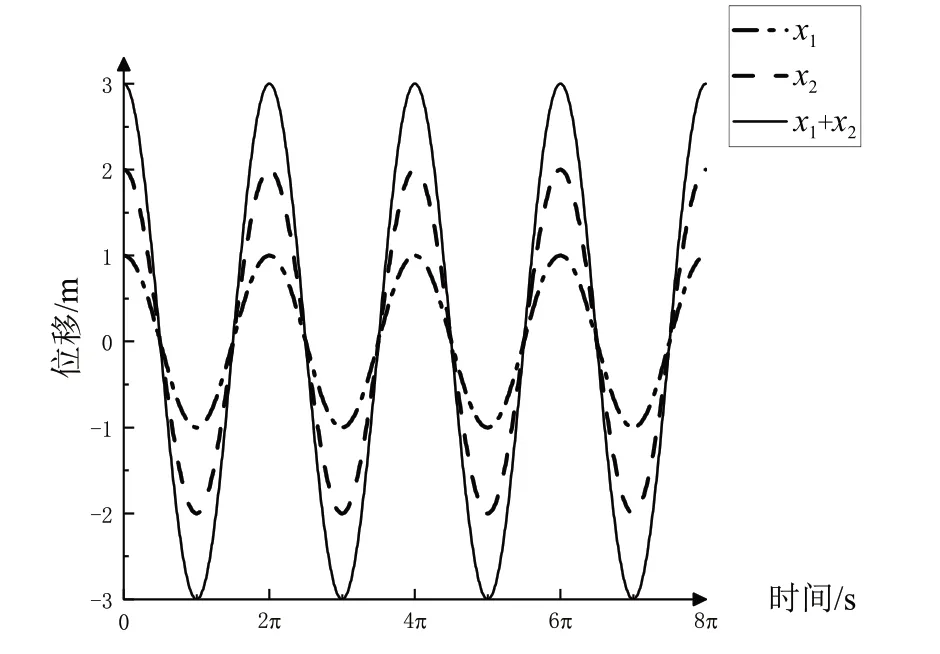
图5 同方向同频率简谐振动的合成
5.1.2 同方向不同频率简谐振动的合成
采用Orign 软件将分振动和合振动进行仿真,具体操作过程如下:首先打开软件新建新的空白图形窗口,设置横坐标范围(0,8π),纵坐标范围(-1.5,2.5),修改横、纵坐标轴标题、刻度及轴的位置;然后分别新建2D 函数图,自变量在(0,8π)中取1000 个点,输入函数Y(x)=cos(x)、Y(x)=cos(2*x)、Y(x)=cos(x)+cos(2*x),仿真曲线如图6;输入函Y(x)=cos(0.50*x)、Y(x)=cos(0.52*x)、Y(x)=cos(0.50*x)+cos(0.52*x),仿真曲线如图7。
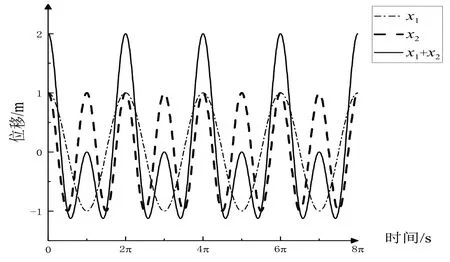
图6 同方向不同频率简谐振动的合成
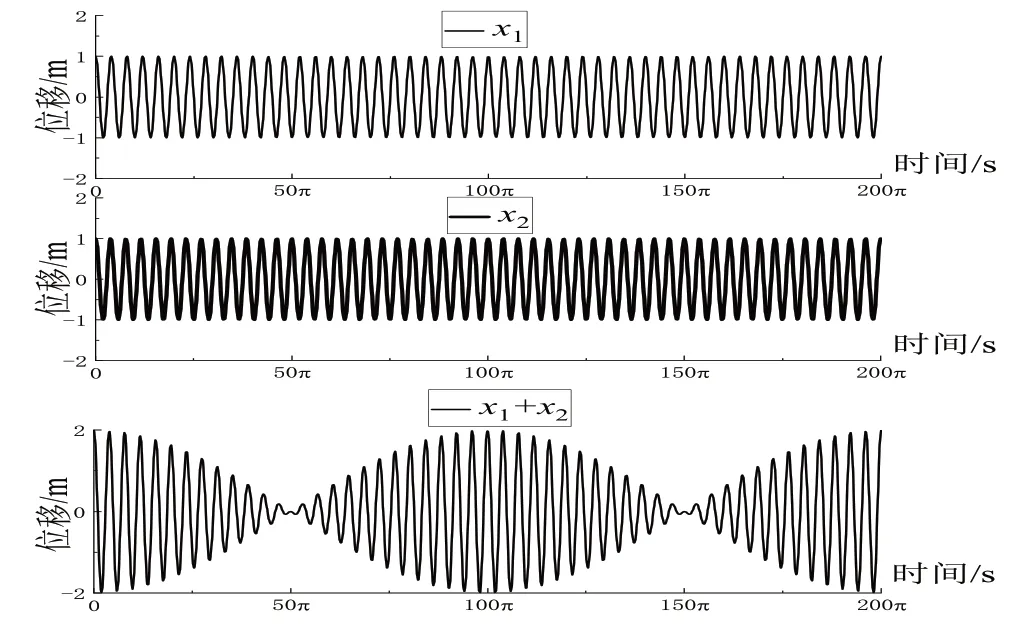
图7 拍现象
5.1.3 互相垂直同频率简谐振动的合成
首先Orign 软件打开软件新建新的空白图形窗口,修改横、纵坐标轴标题、刻度及轴的位置,然后分别新建2D参数函数图,最后将所有曲线合并成3行5列的图形,并将所有的坐标轴隐藏,输出曲线如图8。具体操作如下:
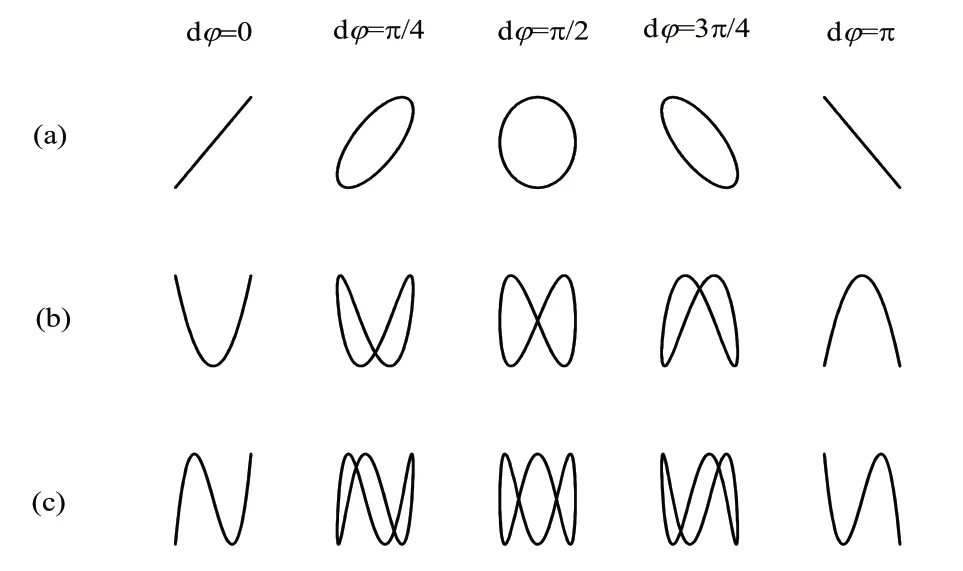
图8 互相垂直简谐振动的合成
设置横坐标范围(-1,1),纵坐标范围(-2,2),自变量(0,2π)取100个点,输入函数[X(t)=cos(t),Y(t)=2*cos(t)]、[X(t)=cos(t),Y(t)=2*cos(t+pi/4)]、[X(t)=cos(t),Y(t)=2*cos(t+pi/2)]、[X(t)=cos(t),Y(t)=2*cos(t+3*pi/4)]、[X(t)=cos(t),Y(t)=2*cos(t+pi)],振动曲线如图8(a)。
设置横坐标范围(-2,2),纵坐标范围(-1,1),自变量(0,2π)取100 个点,输入函数[X(t)=2*cos(t),Y(t)=cos(2*t)]、[X(t)=2*cos(t),Y(t)=cos(2*t+pi/4)]、[X(t)=2*cos(t),Y(t)=cos(2*t+pi/2)]、[X(t)=2*cos(t),Y(t)=cos(2*t+3*pi/4)]、[X(t)=2*cos(t),Y(t)=cos(2*t+pi)],振动曲线如图8(b)。
设置横坐标范围(-1,1),纵坐标范围(-3,3),自变量(0,2π)取100个点,输入函数[X(t)=cos(t),Y(t)=3*cos(t)]、[X(t)=cos(t),Y(t)=cos(3*t+pi/4)]、[X(t)=cos(t),Y(t)=cos(3*t+pi/2)]、[X(t)=cos(t),Y(t)=cos(3*t+3*pi/4)]、[X(t)=cos(t),Y(t)=cos(3*t+pi)],振动曲线如图8(c)。
5.2 结果分析
由图5可见,同方向同频率简谐振动的合振动仍为简谐振动,其频率和分振动的频率相同,合振动的振幅和初相位由分振动的振幅和初相位决定。
由图6可见,同方向不同频率的振动的合振动不是简谐振动,但有周期性。分振动的周期分别是2π和π,合振动的周期为2π,是分振动周期的最小公倍数。特殊情况下,如果两个分振动的频率之和远小于其频率之差,那么合振动可以看作“准简谐振动”,即振幅有周期性变化的“简谐振动”,如图7,分振动的圆频率分别为0.50 rad·s-1和0.52 rad·s-1,频率之和远大于频率之差,合振动的振幅在(0,2)之间缓慢变化,这种现象叫“拍”。
由图8可见,两互相垂直简谐振动的合振动的轨迹的形状由分振动的振幅、频率和初相差决定。当分振动的频率相同时,合振动的轨迹为椭圆,相位相同或相反时,椭圆化为直线;当分振动的频率为整数比时,合成振动的轨迹可以称为稳定的曲线,曲线的花样和分振动的频率比和初相位有关,即得到李萨如图形。
6 结语
简谐振动是最基本的机械振动,物体在线性恢复力的作用下按照正弦或余弦规律作周期性运动。采用Origin 软件仿真可以简便直观地探讨简谐振动的特征,具体如下:
(1)简谐振动的位移、速度和加速度随时间变化的曲线呈现余弦(或正弦)规律,具有周期性。曲线的形状和在坐标轴的位置简谐振动的圆频率和初始条件决定。质点的运动状态也可以用相轨迹来描述,简谐振动的相轨迹是椭圆或圆,其形状和大小由简谐振动的圆频率和初始条件决定。
(2)由于简谐振动的质点只受线性恢复力的作用,运动过程中系统的机械能守恒。动能和势能均按正弦或余弦函数的平方随时间变化。动能最大时,势能最小,动能最小是,势能最大,简谐振动的过程就是动能与势能相互转化的过程,总的能量不变,且大小取决于系统的劲度系数与振幅。
(3)质点同时参与几个简谐振动,则其振动应为几个振动的合成。若分振动同方向同频率,则合振动仍为同方向同频率的简谐振动,其振幅和初相位由分振动的振幅和初相位决定;若分振动同方向不同频率,则的合振动不是简谐振动,但有周期性。特殊情况下,当分振动的频率之和远小于其频率之差,出现“拍”现象;若分振动互相垂直,则合振动的轨迹的形状由分振动的振幅、频率和初相差决定。当分振动的频率相同时,合振动的轨迹为椭圆,当分振动的频率为整数比时,会得到稳定的曲线。
——《势能》

