基于IPSO-ELM 模型的调水工程输水损失预测方法研究
赵然杭,谢文泉,瞿 潇,储 燕,王兴菊,李典基
(1. 山东大学土建与水利学院,山东 济南 250061; 2. 南水北调东线山东干线有限责任公司,山东 济南 253000)
0 引 言
伴随着社会经济的快速发展和全球气候变化的影响,我国面临着诸多水资源问题的挑战[1]。如何提高水资源利用效率,是水利领域亟待解决的问题之一,调水过程中由于各种因素造成的水量损失难以避免[2],而水量损失将降低渠道水利用率,增大运行成本。长距离调水工程水量调度计划中,水量损失是调度计划制定的关键参数[3]。因此准确预测输水损失对于制定精细化调水方案,优化调水工程运行,防治土地盐碱化均有重要意义[4]。
调水工程水量损失计算方法,分为数值模拟法[5,6]、经验公式模型法[7]、现场试验法[8]。数值模拟中为了便于模拟通常对实际情况进行概化,概化后,参数率定理论不明确,模拟结果可能受异参同效性影响,不能较好地反应实际机理;现场试验法中,静水法是在静水条件下测量,不能测验实际输水时的渗漏量[7];动水法在实际输水时完成,但精度差,特别是渗漏量小的区域,测试结果常常偏离实际[9],测渗法的核心是获取渗漏系数,在研究特定点渗漏强度和沿渠道渗漏强度变化时很实用,但计算损失总量并不合理,水深等变化会导致渗漏系数改变[10],以固定值计算总量与实际损失量误差较大,因此现场试验法也有其局限性。
经验公式法由于其结构简单、计算方便的特点得到广泛应用[11,12],但现有的一些简单经验公式估算较大区域尺度下的水量损失时并不适用,如计算衬砌渠道渗漏损失的戴维斯-威尔逊公式和计算土渠渗漏损失的考斯加可夫公式,这些公式最初用于渠道设计[13],研究尺度较小,且大区域尺度下渠道的衬砌条件和地质条件多会沿途改变,导致需要确定的参数数量增多,无法全部准确确定,因此经验公式法难以有效解决复杂的实际工程问题。
还有学者采用回归分析法对引调水工程的水量损失进行拟合,本质上是拟合更精确的经验公式。如胡周汉[14]拟合了南水北调东线一期工程输水水位和输水损失量间的关系,为水量调配提供了依据;田景环[15]拟合了南水北调中线京石段正常输水、冰期输水、汛期输水不同时期入渠流量和输水损失率之间的关系,得出了输水渠道不同输水阶段的损失率规律。
以上研究针对各种形式的河(渠)道输水损失做出了探讨,探究了输水损失的机理和过程,针对不同形式的渠道提出了有效的输水损失计算方法。但仍存在一定局限性,如在计算过程和模型构建上需要大量资料或实验支撑,成本较高,且有些计算方法只适用于某一较小范围区域。因此为了满足计算方法构建简单、计算精确、适用范围广的要求,有必要在已有研究基础上,提出新的河(渠)道输水损失预测方法。
极限学习机 (Extreme Learning Machine,ELM)属于机器学习模型,在拟合变量间关系、解决预测问题等方面有较好表现[16],已被应用于各种领域的预测研究。在水利研究领域,孙淼[17]等将极限学习机应用于洪涝灾害预测,并与传统神经网络模型对比,ELM 模型预测结果均优于传统模型,对洪涝灾害预测效果较好。冯禹[18]等将极限学习机应用于蒸发量预测,很好地反映了气象因子同蒸发量间复杂的非线性关系,模拟精度较高,可作为气象资料缺乏情况下川中丘陵区蒸发量计算的推荐模型。喻黎明[19]等将极限学习机应用于地下水位埋深预测,并与反向神经网络模型对比,基于水均衡理论的ELM 模型能准确反映人类和自然双重影响下地下水系统的非线性关系,在精度、稳定性、空间均匀性上均优于反向神经网络模型,能利用已知资料推求区域空间内其余未知水井的地下水位。
但经具体研究应用发现,当数据集样本较少时,ELM 存在泛化能力不足问题[20],即过度拟合,影响对新数据集的预测效果。精确预测输水损失需要模型有较强的泛化能力,故样本有限时,则需要优化模型性能。而改进粒子群算法有强大的搜索能力,在函数优化、神经网络训练、寻找最优解等领域有较好应用效果[21],能提升机器学习模型性能。因此本文使用改进粒子群算法优化极限学习机 (Improved Particle Swarm Optimization Extreme Learning Machine,IPSO-ELM),增强ELM 的泛化性能。在IPSO-ELM 模型的基础上提出输水损失预测方法并分别与ELM 模型和多元非线性回归模型(Multiple Nonlinear Regression,MNR)的预测结果对比分析。
1 IPSO-ELM输水损失预测方法和模型构建
1.1 极限学习机
极限学习机是一种基于单隐含层前馈神经网络的预测方法[16],由输入层、输出层和隐含层组成,权重和隐含层阈值用于建立相邻两层之间的连接,其结构如图1所示。
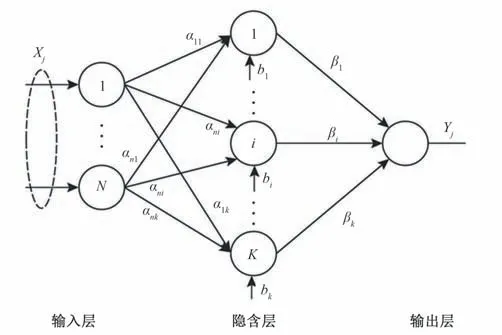
图1 ELM结构图Fig.1 ELM network structure
标准前馈神经网络计算过程如式(1)所示:
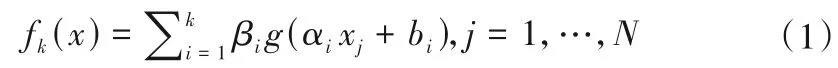
式中:k为隐含层的节点数;g(x)为激活函数;αi为输入层与隐含层第i个神经元之间的连接输入权重;βi为输出层与隐含层第i个神经元之间的连接输出权重;bi是隐含层中第i个神经元的阈值;N为训练样本数。
与传统的前馈神经网络相比,ELM 的输入权重和隐含层阈值是通过随机性随机获得,具有以下优势:①ELM 的学习速度更快;②ELM 减少了局部最小值问题[22]。但由于权重和隐含层阈值随机确定,存在权重和隐含层阈值为0的情况,使得部分隐含层节点失效,出现泛化性能不足问题。
1.2 改进的粒子群优化方法
粒子群算法利用种群中个体的信息共享,使整个种群的运动在求解寻优空间中由无序性逐渐变化为有序性,最终获得最优解。粒子群算法迭代过程中,更新粒子速度和位置的公式如式(2)和式(3):
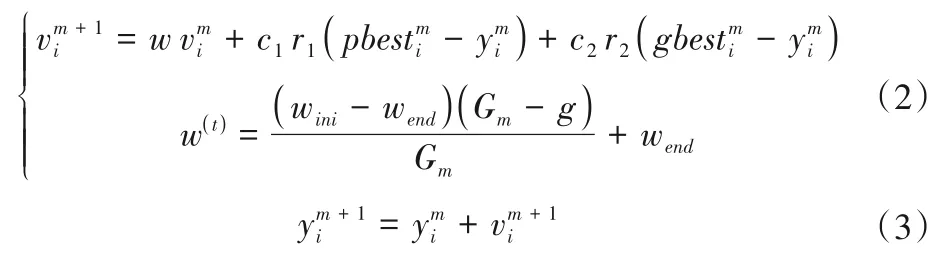
式中:vi为第i个粒子的速度;m为迭代次数;ω为惯性系数;c1和c2为学习因子;r1为r2是(0,1)区间内的随机数;pbesti和gbesti分别为第i个粒子最优解和整个种群最优解。
标准的粒子群算法中,常常采用线性递减策略,而这种策略下的惯性权重无法根据阶段自适应调整;改进的粒子群算法采用非线性的动态惯性权重计算公式,解决了粒子群算法无法跳出局部最优解和振荡的问题[23]。表达式为:

式中:Wmax和Wmin分别为惯性权重的最小值和最大值;f为粒子的适应度;favg为粒子平均适应度;fmin为粒子最小适应度。当各粒子的函数值趋向于局部最优解时,惯性权重增大。相反,当函数值分散时,惯性权重会减小。
学习因子c1和c2表征着粒子活跃程度和粒子间信息共享能力,决定粒子运动方向和收敛结果[24]。标准粒子群算法中,c1、c2∈[0.5,2.5],多根据经验取某一值,不合适的取值会导致大量粒子徘徊于局部。因此,改进后对学习因子进行动态调整,表达式为:
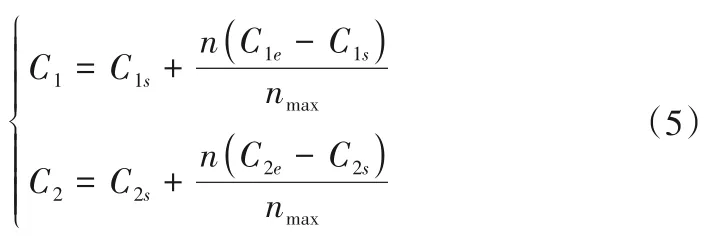
式中:C1s和C2s分别为c1和c2的初值;C1e和C2e分别为c1和c2的终值;n是当前迭代的次数;nmax是总迭代的次数。
1.3 基于IPSO-ELM 的输水损失预测方法
对ELM 而言,寻找最优的隐含层阈值和权重是保证模拟和预测效果的关键。由于极限学习机的泛化能力不足,参数往往难以达到最优。因此,需要采用算法对ELM 进行优化。本文采取IPSO 与ELM 结合的方法,把隐含层阈值和输入权重视作IPSO 粒子,对ELM 进行参数优化处理,即优化ELM 的权重和隐含层阈值,用均方误差作为粒子群算法的适值函数,迭代计算粒子的适应度值,全局搜寻最优值。
用IPSO对ELM参数优化流程见图2,具体步骤如下:
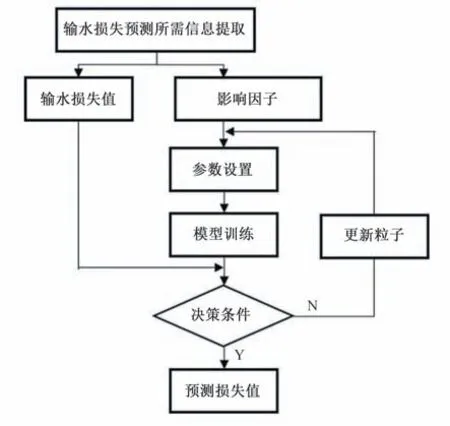
图2 IPSO-ELM 输水损失预测模型流程图Fig.2 Flow chart of IPSO-ELM model for water loss prediction
(1)数据整理与预处理。收集整理调水工程段的输水损失影响因素资料,初始化为影响因素矩阵Xj,j=1,2,…,n;n是影响因素个数。调水工程中水量损失主要是渗漏、蒸发、闸门漏水和渠道退水等,部分因素属于管理问题,不纳入计算,因此输水损失预测主要考虑渗漏和蒸发的影响因素指标,如水深、流量、流速、湿周、水面宽度、水力半径、风速、气温和相对湿度等指标。输水损失指标变量Sk,通过水量平衡法计算,详见式(6),k=1,2,…,l;l是数据组数。
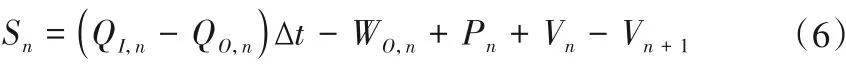
式中:S为日渠段输水损失水量,包含蒸发和渗漏两部分损失,m³;Δt为日调水时长,s;QI、QO分别为渠段入渠流量和出渠流量,m³/s;P为降雨入渠水量,m³;WO为昨日渠段内其他水量变化体积,如灌溉回水或灌溉提水等,m³;Vn和Vn+1分别为第n日早8时时刻和第n+ 1日早8时时刻渠段蓄水体积,m³,蓄水体积根据实测水位和过水面积计算。
(2)筛选影响因素,构建ELM 模型。通过相关性分析和主成分分析筛选影响因素,从n个影响因素中筛选出m个影响因素,此时j=1,2,…,m。利用(Xj,Sk) 构建ELM 预测模型。筛选影响因素方法如下:
(1)相关性分析。为了使指标体系简洁有效,通过相关性分析方法,进行第一次定量筛选,剔除反映信息重复的指标,保证筛选后的指标体系不存在反映冗余信息的指标。步骤如下:①评价指标标准化处理;②计算各个评价指标之间的相关系数;③采用 Barbour 的标准[25],选取临界值M=0.75(0<M<1)。指标间的相关系数|r|≥0.75,说明2个指标高度相关,应根据实际情况删除次要指标。
(2)主成分分析。为了筛选出重要的指标,对相关性分析筛选出的指标进行主成分分析,进行第二次定量筛选。步骤如下:①标准化处理,求标准化矩阵的特征值及特征向量;②建立主成分;按累积方差贡献率p>85%的准则确定主成分个数[26];③计算各指标在主成分上的载荷量,载荷量越大,指标对结果影响越大,则应保留。
(3)构建IPSO-ELM 模型,利用IPSO 优化ELM 参数。根据ELM 的均方误差(Mean Squared Error, MSE)计算粒子的适应度值,并记录对应的个体最佳适应度和群体最佳适应度。将当前粒子适应度值与极值比较,不断反馈更新个体极值和全局极值。
(4)根据式(2)、(3)、(4)、(5)更新粒子,达到最大的迭代次数即可停止,最优适应度值对应的粒子位置即是优化后的ELM两个参数。
2 案例分析
2.1 研究区概况
梁济运河流域位于山东省西南部,属于温带季风气候类型,春、夏、秋蒸发量较大,根据工程地质报告中渠道水位和地下水位相互关系研判,沿线存在渗漏问题,渗漏和蒸发是该工程输水损失的主要组成部分。研究区位置如图3所示。
图3 研究区位置图Fig.3 Location map of study area
南四湖~东平湖段输水工程利用梁济运河输水,输水线路从南四湖湖口至邓楼泵站站下,长58.256 km。其中:0+000~11+000 段采用模袋混凝土护坡,11+000~58+256 段采用现浇混凝土板护坡。断面结构和地质条件如表1所示。
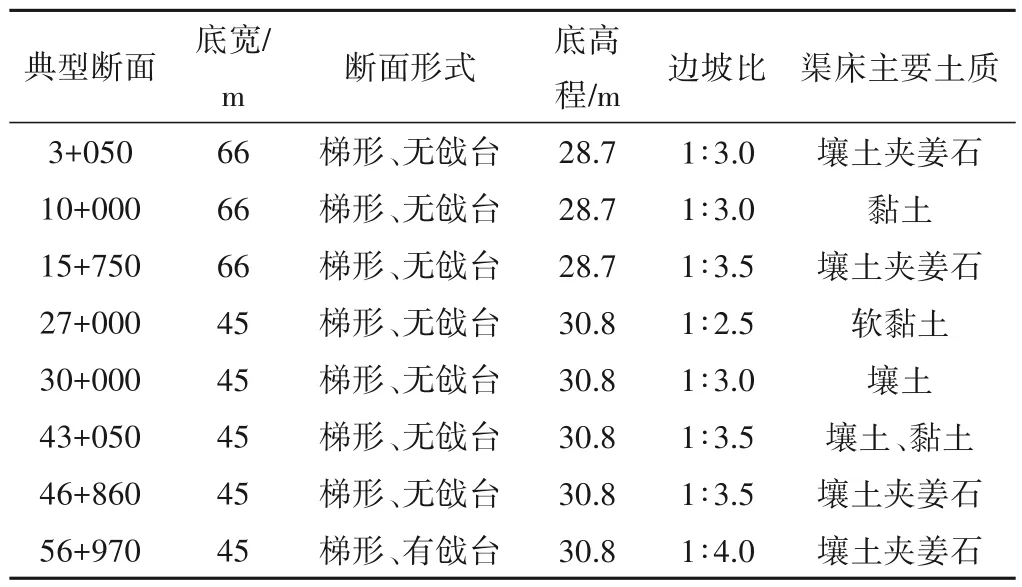
表 1 断面结构与土质Tab.1 Section structure and geology
2.2 影响因素筛选
为避免影响因素反映信息重复,采用Spearman 法对水位、湿周、流量、水力半径、相对湿度、气温、风速、流速、水面宽度等影响因素进行相关分析。当指标高度相关时,根据指标的因果关系或重要性,删除两个指标之一。删减后,保留水位、流量、相对湿度、气温、风速和水力半径为待选指标。
对待选指标进行主成分分析,进一步筛选。方差贡献率表明该主成分传达原始数据信息的百分比,根据主成分选取原则[26],选取累计方差贡献率为88.696%的3个主成分,得到因子载荷矩阵,见表2。根据筛选标准[27],选择载荷值大于0.5 的指标作为代表性指标。
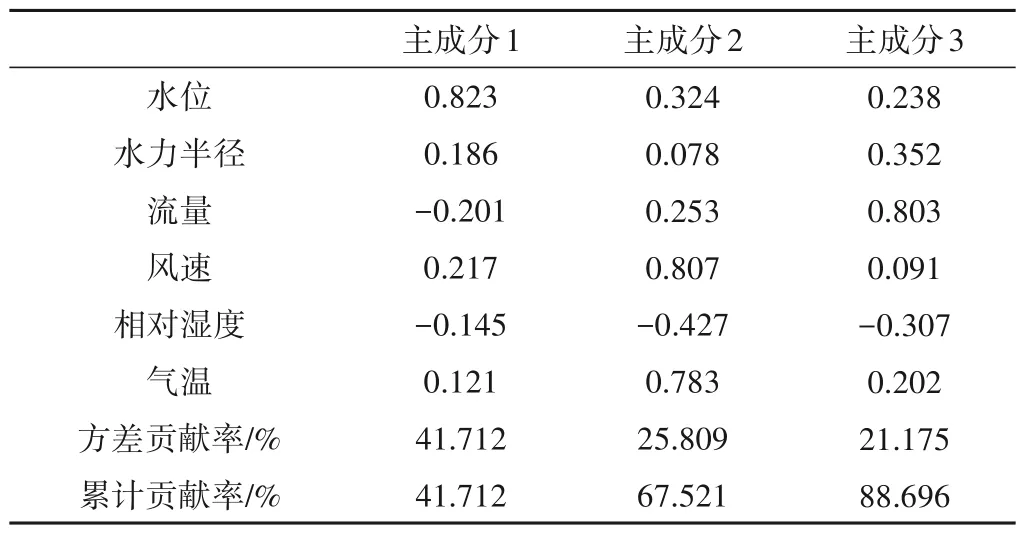
表2 因子载荷矩阵Tab.2 Factor load matrix
经过相关性分析和主成分分析法筛选后保留水深、流量、气温、风速四个影响因素。
2.3 数据来源
实测数据的真实性和可靠性是计算渠段输水损失、保证模型训练效果的关键,本研究收集了2016 年1 月-2017 年6 月南水北调东线梁济运河段泵站运行期间的每日8 时、16 时站前、站后渠道水位和流量等数据,以及沿线各提、退水口流量数据,并对水位和流量监测数据进行一致性检验,剔除不合理监测值。气温和风速等数据通过沿途多个气象站获取。
选取有代表性的典型数据共100 组,包含不同水位、流量、季节的调水情境下的水文气象数据。预留15%不同情境下的数据做预测,包含不同水深、流量、季节下的调水情境,构成测试集。再由程序随机划分70%的数据构成训练集进行机器学习训练,15%的数据构成验证集,以率定模型。
2.4 基于IPSO-ELM 的梁济运河段输水损失预测
建立以输水水深、输水流量、平均气温和平均风速为输入因子,日损失水量为输出因子的预测模型。通过IPSO 算法对ELM初始权重和隐含层阈值迭代寻优。图4记录了种群最优适应度值(均方误差)随迭代次数的变化过程。由图4 可知,IPSO算法群体最优适应度值前期收敛很快,能够快速寻优,经过反复迭代后达到最大迭代次数300 次,最终群体最优适应度值为0.128 6,与之匹配的粒子位置信息即是ELM 的最优输入层权值矩阵和隐含层阈值。
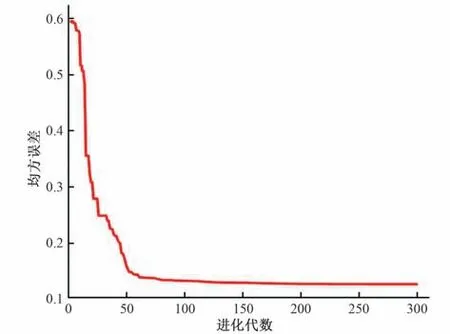
图4 IPSO-ELM 预测模型的最优适应度变化曲线图Fig.4 Best fitness curve of IPSO-ELM prediction model
把包含不同工况的测试集数据输入训练、验证后的IPSOELM 输水损失预测模型,预测结果与真实值的对比和预测值与真实值间的相关分析如图5 所示,预测值和真实值间的确定系数R2=0.962 5,IPSO-ELM 模型对不同工况的预测值和实际值较吻合。

图5 IPSO-ELM 模型预测结果分析图Fig.5 IPSO-ELM model prediction results analysis
2.5 不同模型预测结果对比分析
为了验证IPSO-ELM 预测模型的优越性,预选择经验公式法、多元非线性回归模型和ELM 模型预测结果进行对比分析。由于目前经验公式部分参数难以确定,无法选择经验公式法对比分析,最终选择用MNR 模型和ELM 模型的预测结果对比分析。
(1)MNR预测模型输水损失预测。建立基于多元非线性回归分析方法的预测模型,模型参数通过SPSS(Statistical Product Service Solutions)软件确定,预测公式如式(7)所示。
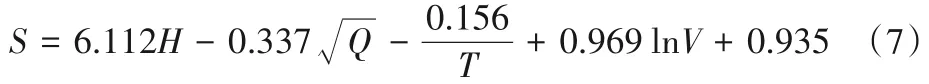
式中:S为日均损失水量,万m³;H为渠道水深,m;Q为渠道流量,m³/s;T为平均气温,℃;V为平均风速,m/s。
拟合结果如表3 所示,MNR 模型公式的确定系数为0.898 6,表明MNR预测模型能够用于输水损失预测。
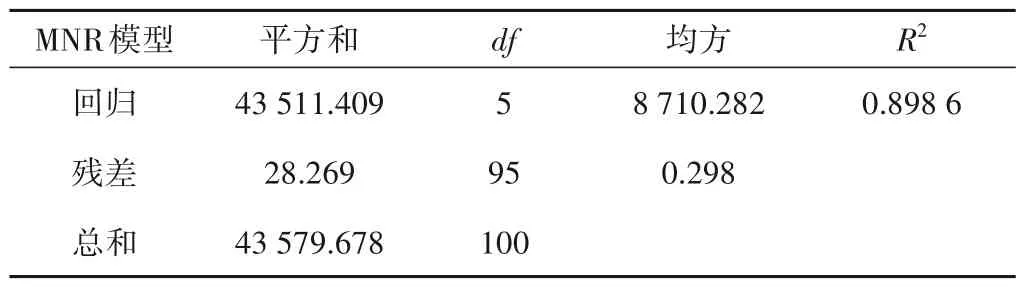
表3 MNR预测模型的拟合结果Tab.3 Fitting results of MNR prediction model
(2)ELM 预测模型输水损失预测。输入测试集数据,ELM模型预测值与真实值对比如图6 所示,与IPSO-ELM 模型相比,预测值和真实值有较大差距,预测结果精度较差。

图6 ELM模型预测值和真实值对比图Fig.6 Predicted value of ELM model and true values comparison
(3)3种模型预测结果对比。将MNR 模型和ELM 模型对测试集的预测结果与IPSO-ELM 模型预测结果进行对比,如图7所示。
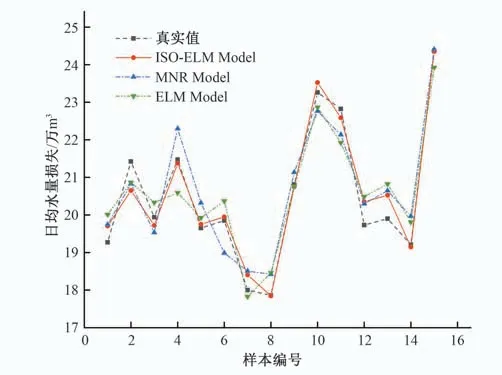
图7 3种预测模型预测结果对比图Fig.7 Comparison of prediction results of three forecasting models
从图7 可知,IPSO-ELM 模型的预测值与实测数据十分接近。ELM 模型和MNR 模型的预测值与实测数据的差异较大,预测稳定性和曲线拟合度较 IPSO-ELM 模型仍有一定差距。
用确定系数R2和平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)评估模型性能和预测精度。R2越接近1,说明拟合优度越高,稳定性越好;MAPE是相对误差度量值,即误差值占真实值的比例,是评估机器学习模型预测性能的常用指标,通常MAPE值越小,误差越小,模型越好。
从表4可以得到:MNR模型、ELM模型和IPSO-ELM 模型的确定系数均大于0.8,表明所建立的3个预测模型均具有较高的拟合优度,结果具有可信度。对比发现,IPSO-ELM 模型预测结果的确定系数R2较ELM 模型和MNR 模型更大,确定系数R2为0.962 5,最接近1,拟合优度最高,稳定性最好,较MNR 模型和ELM 模型分别提高了5.618%和7.111%;对比各预测模型的MAPE值可知,IPSO-ELM 模型预测结果的MAPE值为1.322%,最小,即IPSO-ELM 模型的预测误差最低,较MNR 模型和ELM模型分别降低 52.89% 和 51.06%。
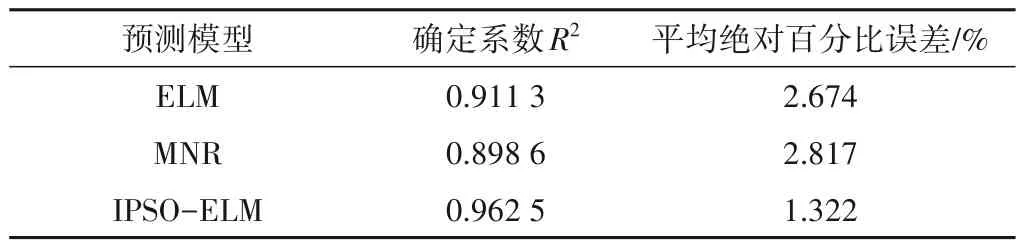
表4 3种模型的预测精度Tab.4 Prediction accuracy for three models
(4)3 种模型泛化能力对比。泛化能力是指模型对新样本的适应性,模型泛化能力越强,实际应用效果越好。一般用预测结果的误差分布判定模型的泛化能力,误差分布范围越小,模型泛化能力越强。不同模型泛化能力对比如图8所示。
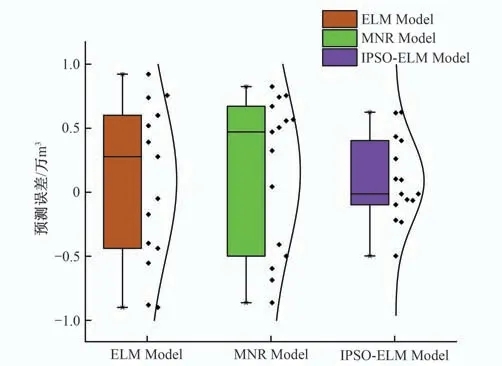
图8 3种模型泛化能力对比图Fig.8 Comparison of generalization capability of three models
箱型图表示数据离散程度,观察箱体发现,MNR 模型的预测误差范围是[-0.85,0.80]万m³,ELM 模型的预测误差范围是[-0.90,0.95]万m³,而IPSO-ELM 模 型 的 预 测 误 差 范 围 是[-0.50,0.70]万m³,主要分布在[-0.25,0.30]万m³内。IPSOELM 模型的预测误差限小于ELM 与MNR 模型,并且大部分预测误差绝对值都小于0.30 万m³。从箱线图右侧的频率分布曲线也可得出同样的结论,说明IPSO-ELM 模型的泛化能力最强,对于新样本适应性最好。
对比分析表明,相对于MNR模型和未优化的ELM 模型,IPSO-ELM 模型能够有效降低预测结果的误差,提高预测模型的预测精度和泛化能力。
2.6 讨 论
(1)基于IPSO-ELM 的输水损失预测方法所需数据容易获取,如水位、流量数据,属于调水工程的基础记录数据;温度、风速等数据,可通过气象站获得。较需要做大量实验确定参数的经验公式法,降低了输水损失预测难度,提高了模型构建效率。从预测结果可以发现,IPSO-ELM 模型充分刻画了输入与输出因子间的非线性关系,较多元回归分析法,拟合优度更高,预测精度更高。
(2)IPSO-ELM 模型的构建效率优于多元回归模型。因调水工程大多跨度较广,沿途地质条件、衬砌形式等条件会有变化,故采用多元回归法时,为较准确地预测不同地质段的输水损失,需要分段建模,进而导致构建过程复杂、效率低。IPSOELM 模型则通过IPSO 对ELM 参数不断迭代调整,能较好地适应沿途条件变化的影响,因此建模效率高。
(3)渗漏损失的主要影响因素是水深、流量、衬砌条件、土壤条件等。对于调水工程,衬砌条件和在时间尺度上基本不变,影响某一区域不同工况下输水损失量的主要因素是水深、流量、土壤含水量等变量;由于缺少土壤含水量数据,可能导致模型预测精度降低。有相关数据后,将在影响因素筛选时考虑更多影响因素,以期更好地反映输水损失,获得更精确的水量信息。
(4)IPSO 进行参数寻优的最大迭代次数可以适当降低,由图4 最佳适应度变化曲线可知,迭代100 次后,最佳适应度值已经十分稳定,这表明可以减少迭代次数且不影响精度,以达到更快速的预测。
3 结 论
在ELM 模型基础上构建了IPSO-ELM 模型,针对预测模型构建复杂和计算精度欠缺的问题为输水损失预测提出一种构建效率高、计算精度高、适用范围广的预测方法,为优化调水工程运行和精准水量规划提供依据。以梁济运河段为例应用该方法,主要结论如下。
(1)建立的IPSO-ELM 输水损失预测模型能较好地用于调水工程输水损失预测。通过改进粒子群算法对极限学习机参数寻优后,在预测精度上有明显提高。IPSO-ELM 模型确定系数R2达到0.962 5,大于0.9;平均绝对百分比误差仅1.322%,小于10%。
(2)IPSO-ELM 输水损失预测模型能适应河(渠)道沿途衬砌形式、地质条件变化的影响,可用于不同复杂形式的调水工程。
(3)基于IPSO-ELM 的预测方法建模效率高,计算速度快,泛化能力优,对新样本的适应能力更强,能准确预测不同调水情境下的输水损失,可以为优化调水工程运行和制定精细化调水方案提供依据,具有推广价值。

