基于改进局部变权理论的底板突水脆弱性评价方法研究

李 哲 ，丁 湘 ，刘守强 ，蒲治国

（1.中煤能源研究院有限责任公司, 陕西 西安 710054；2.中煤冲击地压与水害防治研究中心, 内蒙古 鄂尔多斯 017000；3.中国矿业大学(北京)国家煤矿水害防治工程技术研究中心, 北京 100083）

0 引 言

矿井水害是煤矿五大灾害之一，一旦发生往往造成巨大的生命和财产损失[1]；其中煤层底板突水是矿井水害中的一个重要组成部分，其广泛出现于我国华北及东北地区的大部分矿井[2]，学者将其定义为一种受控于多因素影响且具有非常复杂形成机理的非线性动力现象，目前还没有哪种数学公式能够准确地描述其发生机理[3]。为破解该难题，几十年来国内外学者提出了大量的底板突水预测评价方法，但由于底板突水机理的复杂性，仅有少数评价方法能够应用于生产实际，其中由武强院士提出的基于变权理论的脆弱性指数法是目前最为科学、有效的煤层底板水害预测评价方法，该方法由脆弱性指数法和变权理论2 大基础理论构成，并将2 种理论有机地结合了起来；脆弱性指数法的出现进一步缩减了基于双因素的方法与理论（如突水系数法等）的应用场景，使得底板突水评价的研究出现了跳跃式的发展，并推动了底板突水评价向着信息化、精细化的方向发展，而变权理论的加入又使得因素权重能够根据指标值重新分配，将脆弱性指数法从理论上升华，有效弥补了常权脆弱性评价中各主控因素权重固定这一理论缺陷，使评价结果更加符合实际底板突水规律，代表了目前底板突水评价理论的较高水平[4-6]。但该方法在局部状态变权函数的构建、变权区间及调权参数的确定中存在些许不足，存在一定改进空间。因此，笔者在已有变权脆弱性评价模型的基础上对该模型进行了改进，提出了新型的三区间变权模型，并给出了其参数确定方法，最后以实例评价过程对改进内容进行了展示，证明了本次改进的科学性与可行性。

1 基于局部变权理论的突水脆弱性评价方法

1.1 常权脆弱性指数法

应用于底板突水评价的“脆弱性指数法”由武强院士提出，目前已作为推荐的底板水害评价方法写入《煤矿防治水细则》[7]，该方法以GIS 为技术为平台，在确定底板突水主控因素的基础上结合多源信息融合技术确定主控因素权重，通过煤层底板突水脆弱性评价模型（式(1)）将各主控因素以权重为相对比例进行融合，得到研究区各剖分区域的脆弱性指数，最终根据脆弱性指数阈值对研究区进行突水脆弱性分区[8-11]。

式中：VI为脆弱性指数；Wk为影响因素权重；fk（x，y）为单因素指标值函数；x，y为地理坐标；n为影响因素的数量。

1.2 变权脆弱性指数法

1）局部变权理论。局部变权理论源于变权理论，其核心思想由汪培庄教授[12]于20 世纪80 年代提出；随后，李洪兴[13]给出了惩罚型、激励型、不惩罚不激励型3 种变权的公理化定义及变权计算公式（式(2)）；之后，姚炳学[14]提出应当根据状态值的大小给予不同的变权策略，即局部变权理论。

式中：W(x)为变权权重；Sj(x)为m维状态变权函数；W0=()为常权向量。

2）变权脆弱性评价模型。常权模型体现了单个因素对目标的相对重要程度，具有一定科学性，但是，通常情况下因素对目标的影响权重不仅与因素对目标的重要程度有关，还与因素状态值的大小及其组合状态有关[15-16]，为此，武强院士等将局部变权理论引入到脆弱性指数法权重的确定中来，并总结了底板突水脆弱性变权评价的特点，构建了符合底板突水评价特点的局部状态变权函数（式(4)）及底板突水变权评价模型（式(3)），开创了应用局部变权理论评价底板突水脆弱性的先河[17-18]。

根据式(2)及式(4)可归纳出变权向量的求取过程如图1 所示，在常权向量及因素状态值确定的基础上，变权向量取决于变权区间与变权参数。而目前关于变权区间与变权参数并没有统一的确定方法，文献18 给出了变权区间及调权参数的确定方法如图1 所示。

图1 变权向量求取过程Fig.1 Variable weight vector obtaining process

对于变权区间，采用K-means 法将各主控因素归一数据分类，然后根据各指标分类临界值按照计算公式确定各因素变权区间阈值。对于调权参数，首先，选择或者构建一个满足约束条件的评价单元，其约束条件为各主控因素中4 个指标状态值分别处在4 个不同的变权区间；其次，确定各指标常权权重及其理想变权权重；最后，通过建立方程组解出4 个调权参数[18]。

3）现有突水脆弱性变权模型的特点。基于变权理论的脆弱性指数法由于其评价方法的科学性、评价结果的有效性已成为目前底板突水预测评价方法研究的热点，但由于现有的底板突水评价的变权模型在部分操作上依据不够充分，致使该模型存在改进的空间。如：①将状态变权函数的变权区间分为4 个，与数据大、中、小三分类的常规认识不完全相符；②不同因素的状态变权函数是相同的且不受常权权重的控制，在变权之后不能反映常权权重与权重调整程度之间的正相关关系，会出现常权权重大的因素权重调整程度小、常权权重小的因素权重调整程度大的现象，导致在应用变权理论前后因素权重大小排序改变；③通过聚类分析的方法确定区间阈值依据不充分，聚类分析结果只能指示数据相似、聚集程度，不能反映因素状态值的大小关系；④采用理想变权反算调权参数，在实际操作中较为繁琐复杂，容易出错，甚至有时会出现无解的情况。

1.3 新型的三区间突水脆弱性变权模型

针对现有的突水脆弱性变权模型的特点，对其进行了改进。将局部状态变权函数变权区间调整为三段（式(5)），并在状态变权函数中加入了常权权重与“常权相关系数”，使得每个因素的变权调整规律随常权权重的不同而变化，实现常权权重大的因素变权调整程度大、常权权重小的因素权重调整程度小，避免了出现常权权重小的因素变权权重反而比常权权重大的因素变权权重大的现象，改进后的变权向量求取过程如图2 所示。首次提出了通过分析各因素归一值累积频率确定变权区间阈值的方法（图3），因为，在自然状态下数据出现规律基本符合正态分布，即在数据极小值或极大值附近出现的概率小，而处于中间位置的数据出现概率大。于是，频率大即通常说的“常见”或是“普通”，可认为该数据是中等的，可将其归于不惩罚不激励区间，出现次数少、频率小即通常意义上的“极端”或是“独特”，就可认为该数据要么是大要么是小的，可将其归于惩罚或激励区间，区间阈值的确定方法就转化为了研究因素状态值的频率统计问题，更加符合实际突水规律。在确定调权参数时既然需要以经验为指导，因此，把精力集中放在一个单元上不如把精力放在整体的变权评价结果上；对于变权参数，多数学者是根据经验直接给出变权参数，研究采用先初步给定三区变权模型的参数，然后根据评价结果不断调整确定最终取值。通过以上改进可大幅提升底板突水脆弱性变权评价方法的科学性、可操作性。

图2 改进后的变权向量求取过程Fig.2 Improved process of obtaining variable weight vector

图3 基于累积频率的变权区间确定方法示例Fig.3 Example of the method for determining variable weight interval based on cumulative frequency

其中：x为因素状态值；k为调权参数，又称为常权相关系数；dj1、dj2为第j个因素变权区间阈值；[0,dj1）为惩罚区间；[0,dj2）为不惩罚不激励区间；[dj2,1]为激励区间。

2 实例分析

2.1 研究区概况

研究区位于平朔矿区中南部，目前主采山西组9 号煤层。矿井潜在充水水源为大气降水、地表水、石炭-二叠系砂岩裂隙水、奥灰岩溶裂隙水；井田构造较为发育。9 煤采掘过程中直接充水含水层为顶板石炭-二叠系砂岩裂隙水，其富水性弱突水危险性相对较小，9 煤下伏的奥灰巨厚含水层，该含水层富水性强、水压大，与9 号煤平均间距仅51 m（图4），9 号煤底板最大承压1.27 MPa（图5），经计算9 号煤突水系数虽小于构造区段临界突水系数0.06 MPa/m，但在断层、陷落柱等隐伏垂向导水构造的影响下，仍面临奥灰水害风险，因此，有必要对9 号煤底板奥灰突水脆弱性进行评价，为水害防治工作圈定重点区域。

图4 9 号煤层与奥灰关系示意Fig.4 Schematic of relationship between No.9 coal seam and Austrian ash

图5 9 号煤底板奥灰水带压范围三维示意Fig.5 3D schematic of pressure range of Ordovician water in No.9 coal floor

2.2 基于局部变权理论的底板突水脆弱性评价

1）构建主控因素量化数据库。参照武强院士总结出的5 大类底板突水影响因素，经过对研究区实际地质及水文地质条件的详细分析，结合以往华北煤田煤层底板奥灰水害评价经验，确定出研究区煤层底板奥灰含水层突水脆弱性主要控制因素有7 个：①奥灰含水层水圧；②奥灰含水层富水性；③有效隔水层等效厚度；④矿压破坏带下脆性岩厚度；⑤底板岩芯采取率；⑥构造分布；⑦断层规模指数。各主控因素经量化、插值，借助ArcGIS 平台绘制等值线图（图6-图8），经归一化处理最终建立了主控因素数据库。

图6 奥灰含水层水压等值线Fig.6 Contour plot of Ordovician aquifer water pressure

图7 底板有效隔水层等效厚度等值线Fig.7 Contour plot of equivalent thickness of effective water barrier of bottom plate

图8 断层规模指数等值线Fig.8 Contour plot of fault scale index

2）确定常权权重。采用层次分析法确定各主控因素的常权权重。通过分析研究区煤层底板奥灰突水脆弱性的各主控因素，将其划分为3 个层次（图9），然后在征集专家意见的基础上确定各因素之间的相对重要程度，采用具有心理测试实验作为基础的9/9-9/1 标度将专家自然语言转化为量化分值，由此构建煤层底板突水脆弱性AHP 评价的判断矩阵，并采用基于Matlab 编写的AHP 计算软件对判断矩阵进行求解、层次排序及一致性检验（图10）[19]，最终获得主控因素与底板突水脆弱性之间的常权权重（表1），图10 中CI 为安全一致性指标，RI 为随机一致性指标，CR 为一致性比率。

表1 底板突水脆弱性主控因素常权权重Table 1 Constant weight of main controlling factors of floor water inrush vulnerability

图9 层次结构模型Fig.9 Hierarchical model

图10 AHP 法权重计算界面Fig.10 AHP method weight calculation interface

3）确定变权区间及调权参数。采用分析因素归一值累积频率的方法确定变权区间，由于目前未曾定义过出现频率为多少才可归为“极端”或是“独特”的数据，本次暂且将状态值累积频率的界限定为33%、67%，即归一值累积频率33%对应的归一值为惩罚区间与不惩罚不激励区间的界限值，归一值累积频率67%对应的归一值为不惩罚不激励区间与激励区间的界限值。绘制各主控因素状态值频率累积区间即可确定变权区间阈值（图11-图13），其中受人为因素影响较大的因素可通过人为指定的方法来确定。最终区间阈值分类标准见表2。对于调权参数根据已往的经验，先初步给定三区变权模型的参数，然后根据评价结果不断调整确定最终取值。表3 展示了最终确定的变权模型调权参数。

表2 主控因素变权区间划分Table 2 Main control factor variable weight interval division

表3 调权参数最终取值Table 3 Final value of weighting parameter

图11 奥灰含水层水压累积频率Fig.11 Accumulative frequency of water pressure in Ordovician aquifer

图12 等效厚度累积频率Fig.12 Construct a distribution cumulative frequency

图13 脆性岩厚度累积频率Fig.13 Cumulative frequency of brittle rock thickness

4）构建变权评价模型与评价分区。根据计算获得的主控因素变权权重值，结合主控因素量化数据库，建立了研究区基于局部变权理论的煤层底板奥灰突水脆弱性评价模型（式(6)），如下：

根据上述变权评价模型对研究区突水脆弱性进行了评价，评价结果如图14 所示，同时采用常权脆弱性指数法得到的评价结果如图15 所示。对比2种评价结果黑色方框内区域，该区域在常权模型时由于等效厚度、脆性岩厚度大为较安全区，在变权模型时被划分为较脆弱区、过渡区，主要原因是该区域的水压较大，变权模型对其权重进行了“激励”，由常权的0.271 9 增加至0.4～0.46，评价结果更加突出水压对底板突水脆弱性的控制作用。从评价过程及评价结果上可以看出本次构建的三区间变权模型及其参数确定方法能够实现变权模型对权重的调整作用。

图14 基于新型变权模型的脆弱性评价分区Fig.14 Vulnerability assessment partition based on a new variable weight model

图15 基于常权模型的脆弱性评价分区Fig.15 Vulnerability evaluation zone based on constant weight model

3 改进的变权模型权重调整规律分析

3.1 变权模型权重调整特征

通过对比变权评价与常权评价分区结果，可以直观的看出变权模型可以体现指标状态值大小及不同状态值组合对权重的影响，而评价分区结果的差别受控于权重。以下就从权重的区别上来更加深入的分析变权模型的权重调整特征。

连续改变7 个主控因素中某一个因素的归一值，其余6 个因素归一值固定不变，采用常权模型计算脆弱性指数，绘制指标值与脆弱性指数的关系如图16 所示。由图16 中可以看出脆弱性指数随各指标归一值的增大而均匀增加，表现出各因素与底板突水脆弱性之间为线性相关关系。

图16 常权模型脆弱性指数与归一值关系Fig.16 Relationship between vulnerability index and normalized value of constant weight model

然后，使相同方法研究变权模型对多源主控因素的耦合效果，绘制脆弱性指数与归一值之间的关系如图17 所示，由图17 可以看出基于变权模型的脆弱性指数增加方式变成了曲线，指标归一值越大或者越小曲线的斜率就越大，斜率即体现了权重的大小，反映变权模型能够使得权重随着指标值的变化进行调整，显示出变权模型中各因素与底板突水脆弱性之间为非线性相关关系，从而使得脆弱性指数法更加接近因素与底板突水脆弱性间的实际关系。

图17 变权模型脆弱性指数与归一值关系Fig.17 Relationship between vulnerability index and normalized value of variable weight model

图18 是通过改变一种因素指标值固定其余六个因素模拟出的变权模型各变权区间权重变化图，即是图17 中曲线的斜率，展示了各变权区间权重值的变化，由图18 中可以看出变权模型达到了对小值惩罚、对大值的激励作用。

图18 各主控因素变权权重变化曲线Fig.18 Variable weight change curve of each main control factor

3.2 权重调整特征与常权关系

三区间模型与四区间模型的最大区别是在状态变权函数中加入了常权权重及常权相关系数，常权权重的加入使得各变权区间权重的调整特征与常权权重产生正相关关系，常权相关系数则可以调整这种正相关相关关系的紧密程度，以下就来说明三区间模型是否能够体现变权程度与常权权重的正相关关系。变权模型可以增大激励区间的权重是上节确定的权重调整特征之一，本次暂且以强激励区间变权权重增大率来表示变权程度。

将现有的四区间模型及新型的三区间模型各指标变权区间阈值设为相同值，改变7 个因素中一个因素的归一值，其余6 个因素归一值固定不变，获得在不同变权模型下不同指标的激励（强激励）区间权重增长百分比，并据此绘制出图19。由图19 可以看出在四区间模型中，常权权重0.271 9 的指标在激励区间权重增大率可以达到75.48%，常权权重为0.068 8的权重增大率却为122.28%，权重增加程度与常权权重呈负相关关系，而在三区间模型中，权重增加程度与常权权重有着明显的正相关关系。这就说明，未考虑常权权重的现有四区间模型权重调整程度不能体现常权权重大的指标激励（惩罚）的幅度大，反而出现常权权重大的权重调整程度小，常权权重小的权重调整程度大，最终可能使得权重均一化严重；而考虑常权权重的新型三区模型权重调整程度与常权权重呈正相关关系，达到了预期目标，实现了常权权重大的指标在变权时惩罚和激励的幅度要相应增大的初衷。

图19 权重调整程度与常权权重关系Fig.19 Relationship between degree of weight adjustment and constant weight

3.3 调权参数灵敏度分析

灵敏度分析可以有效的确定对系统造成重要影响的参数及其影响作用，给出哪些参数的影响是比较大的、哪些是由于输入的变化对输出造成的影响等等，对提高模型精度具有重要意义[20-21]。

研究在状态变权函数中加入了常权相关系数k，使得变权模型的参数变为了a1、a2、c及k。文献[17]已对现有变权模型中的调权参数a1、a2、a3及c进行了详细的灵敏度分析研究，研究只对参数k进行灵敏度分析。参数灵敏度分析可分为全局灵敏度分析及局部灵敏度分析，其中局部灵敏度分析操作简便、计算量适中，能够分析单个因素对系统造成的影响[22]。研究采用局部灵敏度分析的方法对k值进行分析，以上文确定的k=0.1 为基准，使得k值变化范围分别为 ±10%、±20%、±30%，其余调权参数以表5 中为准，变权区间长度值定为统一的0.33，然后研究新型变权模型变权程度与k值及常权权重之间的关系。

图20 显示了不同k值状态下，变权程度与常权权重之间的关系。可以发现，当常权权重较小时，在任何k值条件下常权权重与权重调整程度正相关关系非常明显，随着常权权重的增大，常权权重与权重调整程度正相关关系相对变弱，当k值增大30%（k=0.13）时，权重0.247 5 的因素在激励区间权重增大程度开始大于权重为0.271 9 的指标。因此，可以得出以下结论：常权相关系数k具有控制权重调整程度的作用，并与权重调整程度呈正相关，k值也可控制常权权重与权重调整程度的正相关关系，k值越小正相关性越强，反之越弱，当k值增大到一定程度时，则不能使常权权重与权重调整程度呈正相关。

图20 权重调整程度与常权权重关系Fig.20 Relationship between degree of weight adjustment and constant weight

为确定当k为何值时才能使得权重调整程度与常权权重呈正相关关系，采用MATLAB 软件编程，同时连续变化k值（0～0.5）及常权权重（0～0.8），计算变权权重在激励区间的增大程度，获得了不同常权权重、k值对应的权重增大程度，并绘制了图21。由图21 中可以看出：常权权重一定时，随着k值的增大权重调整程度逐渐增大，但是不同常权权重的增大速度不同，权重越大增大速度越小，当k大于某一值时，常权权重小的增大程度反而大于常权权重大的增大程度，即在图的横向上，k值一定时随着常权权重的增大，权重提高百分比是先上升后降低。而且随着k值的增大，能够保证权重提高百分比是上升阶段的常权范围越小。根据得到的数据可以获得每个常权对应的k值界限值，将点投在图上连接为线即为图中的红线。将常权对应的k值界限值绘制成散点图（图22），求出拟合线近似为直线，该直线表达式为：

图21 常权权重、k 值与变权程度关系Fig.21 Relationship between constant weight, k and variable weight

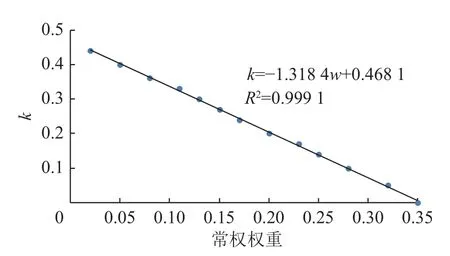
图22 k 值界限值与常权权重拟合关系Fig.22 Fitting relationship between k boundary value and constant weight

该拟合线表示：当权重w（2 个指标常权权重均值）一定时，k的取值小于式(7)中结果kmax（k值界限值）才能使得权重调整程度与常权权重呈正相关。例如，常权权重为0.271 9、0.247 5，计算的得出的k为0.125 7，在上述实际值0.12～0.13 范围内，因此，式7 可用于常权相关系数k值的确定中。

4 结 论

1）针对基于变权理论的底板突水脆弱性评价难题，构建了新型的三区间局部状态变权函数，并在函数中加入了常权权重及常权相关系数，首次提出了通过分析因素指标归一值累积频率确定变权区间阈值的新方法，采用了先初步给定变权模型的参数，然后根据评价结果不断调整确定最终取值的调权参数确定方法。

2）采用新模型、新方法实现了对研究区底板突水脆弱性的变权评价，通过展示评价过程、对比评价结果与常权模型评价结果，说明新模型、新方法是可行的，能够科学、简便地实现突水脆弱性的变权评价。

3）通过对变权权重调整规律的研究证实了新型三区间变权模型能够实现权重调整程度与常权权重呈正相关关系，并通过灵敏度分析的方法确定了常权相关系数的限定条件。