含裂隙煤体能量耗散特征与冲击倾向性研究

朱志洁 ，李瑞琪 ，汤国水 ，韩 军 ，王来贵 ，吴云龙

（1.辽宁工程技术大学 矿业学院, 辽宁 阜新 123000；2.煤炭科学研究总院 煤炭资源高效开采与洁净利用国家重点实验室, 北京 100013；3.滁州职业技术学院 组织人事处, 安徽 滁州 239000）

0 引 言

煤岩冲击倾向性是指煤岩体弹性应变能聚集到一定程度超过其强度极限值后瞬间释放的动态冲击破坏的能力。冲击倾向性是煤岩体是否能够发生冲击地压或岩爆的自然属性[1]，是评价煤岩体冲击地压或岩爆发生危险的重要依据[2]。

近50 年来，国内外专家和学者对煤岩体冲击倾向相关理论开展了诸多研究工作。冲击倾向性受到煤体外部和内部多种因素的共同影响。赵毅鑫等[3]研究了煤体内部细观结构特征、有机组分分布与煤体冲击倾向性的定量关系。赵同彬等[4-5]分析了破坏过程中的能量积聚与释放规律，研究了不同均质度的煤岩冲击倾向性。孟召平等[6]研究含水量对岩石力学性质及其冲击倾向性的控制机制，建立岩石力学性质及其冲击倾向性与含水量之间的相关关系和模型。张志镇等[7]通过不同温度条件下的断口电镜扫描和单轴压缩试验，研究了温度对花岗岩冲击倾向性的影响。张广辉等[8-10]测定了不同瓦斯压力煤体的冲击倾向性指标，分析了瓦斯对煤体冲击倾向性的影响。左建平等[11]通过单轴压缩试验研究了不同煤岩体组合条件下的破坏和强度特征，得到了煤岩体组合方式对冲击倾向性的影响机制。邓志刚等[12-14]通过数值模拟等方法对不同尺寸的煤体试件进行了单轴压缩测试，研究了煤体冲击倾向性和强度特性的尺寸效应。卢志国等[15-17]分析不同层理角度下煤样冲击倾向性指标值的变化，探讨了层理对煤冲击倾向性的影响及内在机理。在冲击倾向性指标方面，国内外学者从强度、能量和时间等角度提出了多种评价指标。SZECOWKA 等[18]提出了应变能储存能力指标，即煤体试件在加载过程积蓄的弹性能量与卸载过程消耗塑性能量的比值。GIL 等[19]将单轴压缩下破碎煤体的动能与最大累积应变能比值定义为冲击效率比，对煤体冲击倾向性进行评价。SINGH[20]提出了冲击能量释放指标，即单轴压缩试件破坏时监测到3 个方向震动速度的矢量总和。唐礼忠等[21]将剩余能量与峰值强度后稳定破坏所需的能量耗散之比定义为剩余能量指数，该指标反映岩石在峰值强度后的动态破坏特性。张绪言等[22]指出煤岩冲击倾向性是一个关于能量与时间的函数，提出了剩余能量释放速度指数。陈卫忠等[23]提出岩体实际储存能量与极限能量之比为可作为岩爆的能量判别指标，该指标可真实反映地下工程开挖卸荷过程中岩爆发生的剧烈程度。卢志国等[24]提出了综合考率煤体强度、能量演化及破坏时间的有效弹性能释放速率指数KET 评价煤的冲击倾向性，并结合现有指标给出冲击倾向性分类临界值。宫凤强等[25]提出了一种计算岩石材料在峰值强度时储存在岩石内部弹性能的方法，建立一种基于峰前弹性能密度和峰后破坏能密度的差值即剩余弹性能指数的岩爆倾向性判据。王超[26]提出了综合考虑能量演化过程及时间效应的有效冲击能量速率指数。唐礼忠等[27]从岩石的变形和破坏过程中的能量储存和能量耗散出发，提出岩石的单轴抗压强度与单轴抗拉强度之比值与峰值前后的应变量之比值的乘积作为岩爆倾向性指标。GONG[28-29]提出了峰值强度应变能存储指数和剩余弹性能量指数，分别定义为试样的峰值强度处弹性应变能密度与耗散应变能密度之比和峰值弹性应变能密度与峰值破坏后能量密度之差。姚精明等[30]根据盈余能量和煤样峰值损伤因子的大小，对煤层的冲击倾向性进行了分级。HOMAND[31]将应力-应变曲线应力峰值前、后曲线的斜率定义为刚度模量(E)和降低模量(M)，提出降低模量指数(E/M)作为冲击倾向性指标。张万斌等[32]认为煤样破坏时间可综合反应能量积蓄与耗散动态特征，提出了动态破坏时间可评价煤岩体的冲击倾向。潘一山等[33]提出了考虑时间效应的临界应力系数、临界软化区域系数、冲击能量速度3 项新的指标。代树红等[34]研究了模量指数同其它冲击倾向性评价指标和评价结果的相关性，认为模量指数可用于煤的冲击倾向性评价。齐庆新等[35]在大量统计数据分析基础上，提出将煤岩体的单轴抗压强度可用来评价煤层冲击倾向性。

目前，针对煤岩冲击倾向性的研究已经取得了极大进展，研究成果主要针对于新指标、新方法及其影响因素。然而，在自然界煤岩体中往往存在大量的节理、裂隙等结构弱面，结构面的形态特征（裂隙的角度、尺度、形态等）对煤岩体的失稳破坏有明显的影响，裂隙煤岩体的力学特性具有明显的非连续性、非线性和各向异性。研究含结构面的冲击倾向性更符合现场实际，能更真实地反映煤体破坏失稳过程。采用颗粒流PFC2D（Particle Flow Code in 2 Dimensions）数值模拟方法，对不同裂隙类型煤体试件进行了单轴压缩测试，分析了倾角对宏细观力学参数、能量耗散和冲击倾向的影响规律，研究结果可用来指导冲击地压的预测和防治工作。

1 裂隙煤体应力-应变曲线特征与能量耗散分析

煤体裂隙的张开、闭合、扩展以及贯通的演化过程伴随着能量的转移和释放，该过程对煤体能量储存特征和冲击地压的发生具有重要影响。含裂隙煤体加载过程中裂隙演化和应力-应变关系如图1所示，根据裂隙扩展特征可将加载过程划分为以下5 个阶段：

图1 含裂隙煤体裂隙演化过程的应力-应变曲线[36]Fig.1 Stress-strain curve of fracture evolution process of fissured coal body[36]

1) 裂隙压密阶段(OA段) 。本阶段随着轴向应力增加，煤体内部原始孔隙、裂隙结构逐渐闭合，煤体内部的摩擦耗能现象逐渐减弱，能量积聚能力逐渐增强。该阶段应力阀值为裂隙闭合应力σcc。

2) 弹性阶段(AB段)。煤体内部已有的孔隙和裂隙结构完全闭合后，进入弹性变形阶段(AB段)。该阶段无明显的裂隙扩展现象，系统输入的总应变能基本都转化为煤体的弹性应变能。

3) 裂隙稳定扩展阶段(BC段)。随轴向应力逐渐增大至煤体的启裂应力σci，新裂隙开始产生、原有裂隙开始扩展，应力-应变曲线进入裂隙稳定扩展阶段(BC段)。在该阶段煤体在宏观和微观上均发生不同程度的损伤，承载能力有所降低。在BC段煤体裂隙扩展耗散部分能量，但该阶段煤体仍以能量积聚为主，煤体仍具有一定的承载能力。

4) 裂隙加速扩展阶段(CD段)。当轴向应力逐渐增大至煤体损伤应力σcd时，应力-应变曲线进入裂隙不稳定扩展阶段(CD段)。裂隙进一步萌生和扩展，裂隙煤体的整体强度有所下降。裂隙的加速扩展不仅对岩体结构的力学特性有一定的弱化作用，还会使更多输入的能量以驱动裂隙加速扩展的形式耗散，进而降低了煤体积聚能量的能力。

5) 峰后破坏阶段。随轴向应力继续增大，岩石内部微裂隙交互贯通并形成宏观张裂带或剪切带，岩石试样发生宏观破坏，此时对应的轴向应力为岩石的峰值强度σp。当应力达到峰值强度后，弹性应变能曲线突降，耗散能突增。

2 含裂隙煤体数值模型的建立

2.1 PFC 数值模拟方法

二维颗粒流程序(Particle Flow Code，PFC)是通过离散单元法来模拟圆形颗粒介质的运动及其相互作用，它能模拟煤岩体的细观特征、从本质上反映煤岩的宏观力学行为。在PFC2D数值模拟中，煤岩材料可通过黏结在一起的刚性颗粒进行模拟，颗粒之间的相互作用主要通过2 种内置的微观接触模型：接触粘结模型和平行黏结模型。接触黏结模型只能进行力的传递，而平行黏结模型同时传递力和力矩。平行黏结在拉应力达到抗拉强度或者剪应力达到抗剪强度，颗粒之间的连接都会断裂，平行黏结接触模型能更真实的反映煤岩体的力学行为。

通常，在PFC 数值模拟软件中，采用移除节理两侧接触的方式来模拟节理。裂隙相对两侧的颗粒将沿颗粒周边滑动（图2a），导致裂隙上的固有粗糙度与实际不符的力学行为[37]。为克服这一缺陷，Cundall 建立的平滑节理接触模型[38]，连接的粒子可以沿着裂缝方向穿过并彼此重叠（图2b）可以很好地反映节理的力学性能。国内多位学者也采用了该本构模型对节理裂隙进行了模拟，模拟结果与实际情况相吻合[39-41]。

图2 PFC 中模拟节理的2 种方法示意[37]Fig.2 Schematic of two methods for simulating joints in PFC[37]

2.2 细观参数标定

PFC2D中颗粒接触和内部预制裂隙分别采用平行黏结模型和光滑节理模型。微观参数通常采用“试错法”进行标定。采用MTS815 试验机对50 mm×100 mm 完整煤体试件和与之力学性能相匹配的含预制裂隙试件进行单轴压缩测试，监测得到加载过程中的应力应变曲线。通过反复调试，使模拟得到的应力应变关系与实验室数据相互吻合，获得PFC2D模型中的微观参数如下：颗粒最大、最小半径为0.5 mm 和 0.3 mm，颗粒有效模量2 GPa，颗粒的刚度比1.35，颗粒摩擦系数0.5，平行黏结模量2 GPa，平行黏结刚度比1.35，平行黏结抗拉强度的均值5 MPa，平行黏结抗拉强度的标准偏差1 MPa，平行黏聚力的均值10 MPa，平行黏聚力的标准偏差2 MPa。

如图3 所示，给出了实验室与PFC 模拟标定的单轴压缩应力应变曲线对比情况，数值模拟曲线与试验曲线较为吻合。数值模型和试验测试之间宏观力学参数的比较见表1，模拟的单轴抗压强度和弹性模量与试验获得的数值相似。3 种裂隙数值模型的破坏模式与试验测试得到的破坏模式基本相同，数值模型可以较好反映煤岩体实际破坏情况，该模型可用于相关研究。

表1 宏观力学参数对比Table 1 Comparison of macro mechanical parameters

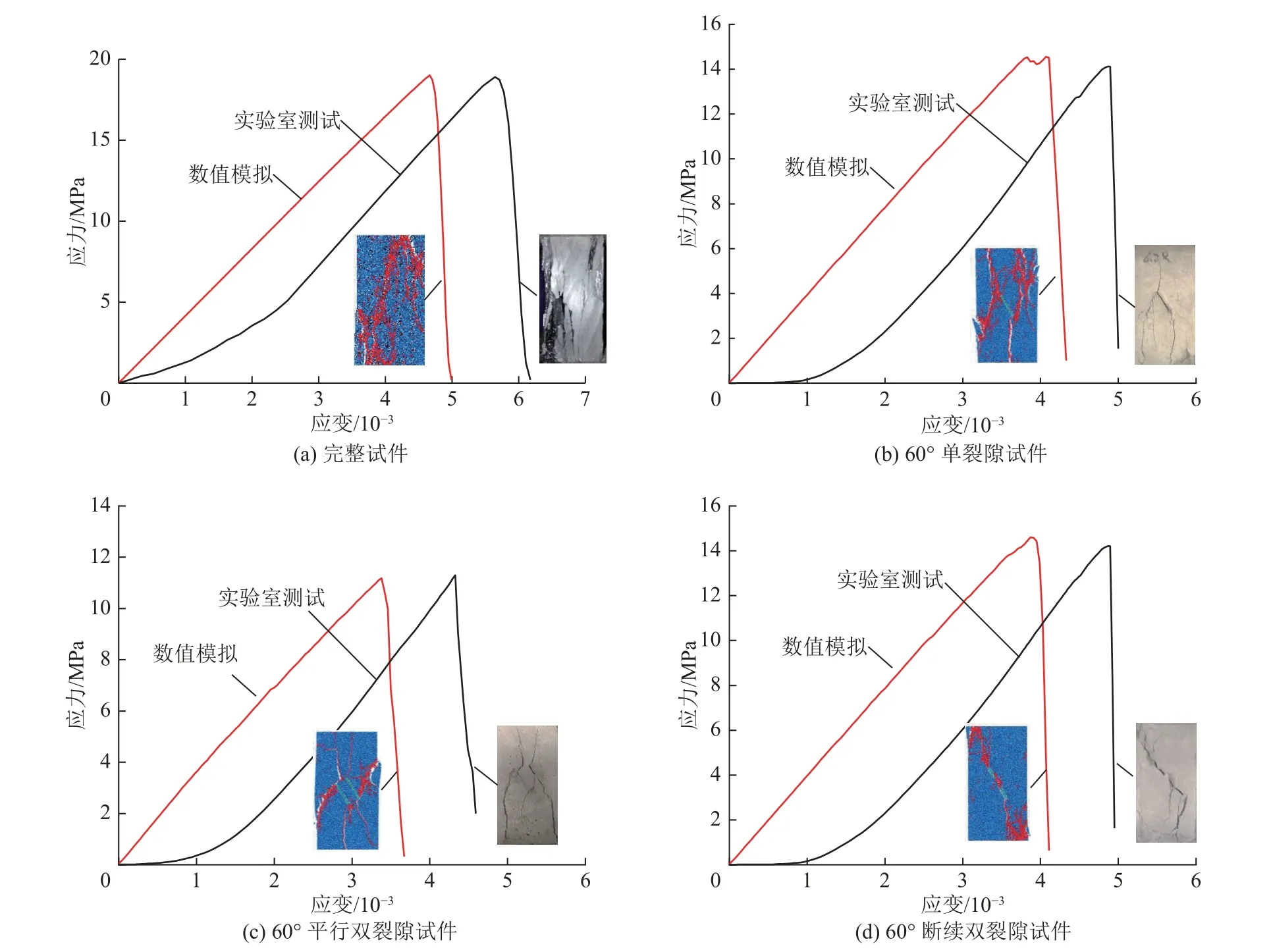
图3 完整与含裂隙试件数值模型的应力应变关系验证Fig.3 Verification of stress-strain relationship of numerical model of intact and cracked specimens

2.3 模拟方案

模拟含裂隙煤体试件的宽度和高度分别为50 mm和100 mm。采用单轴压缩加载方式，对试件进行加载测试，加载速率为0.01 μm/s。在加卸载过程中，对试件的应力应变关系、裂隙发育情况进行实时监测。对不同类型的裂隙进行模拟，裂缝参数如下：①单裂隙试件裂隙长度l= 20 mm，裂隙倾斜角β= 0°，15°，30°，45°，60°，75°，90°; ②共面断续双裂隙试件的裂隙长度l=10 mm，间距为10 mm，裂隙倾斜角β同上；③非共面平行双裂隙试件的裂隙长度l=20 mm，裂隙间距为10 mm，裂隙倾斜角同上。共面断续双裂隙（长度10 mm）与单裂隙（长度20 mm）对比，是为了分析相同裂隙长度断续裂隙和完整裂隙的区别；非共面平行双裂隙（长度20 mm）与单裂隙（长度20 mm）对比，是为了分析相同裂隙长度不同数量的影响。建立的数值模型如图4 所示。

图4 数值模型与裂隙参数Fig.4 Numerical model and fissure parameters

3 含裂隙煤体不同裂隙分布的宏细观力学特征

3.1 宏观力学特性

煤岩体的宏观力学特性与其冲击倾向性密切相关，抗压强度、弹性模量越大，积蓄弹性能越高，冲击倾向性越强。不同裂隙类型煤体试件单轴压缩下的应力-应变曲线如图5 所示。裂隙倾角和分布对全应力-应变曲线特征影响显著。0°、15°、75°和90°裂隙的试件在峰值强度附近由于裂隙发育扩展出现轻微震荡，30°、45°和60°试件在邻近峰值处产生了锯齿状水平波动，并且在峰值前后均存在一定的波动。同时，随着竖向的加载，不同裂隙倾角的试件在相同应变位置的轴向应力也存在一定差异，进而对煤体的宏观力学参数弹性模量和单轴抗压强度具有一定的影响。图6 给出了单轴压缩下不同裂隙类型试件宏观力学参数对比情况。裂隙倾角从0°增加到30°，抗压强度和弹性模量逐渐降低；裂隙倾角30°时，试件的抗压强度和弹性模量为最低值；裂隙倾角从30°增加至90°，抗压强度和弹性模量逐渐升高。从不同裂隙类型来看，不同裂隙类型的抗压强度和弹性模量的大小关系为：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件。

图5 单轴压缩下不同裂隙类型试件的应力-应变曲线对比Fig.5 Comparison of stress-strain curves of specimens with different fissure type under uniaxial compression

图6 单轴压缩下不同裂隙类型试件宏观力学参数对比Fig.6 Comparison of macro-mechanical parameters of coal specimens with different fissure type

3.2 细观力学响应

不同裂隙煤样在宏观力学性能表现出明显差异，其根源在于不同裂隙作用下细观力学响应的不同。图7 给出了不同裂隙类型煤体试件接触力分布情况。以单裂隙试件为例对不同倾角预制裂隙煤体的应力分布特征进行分析：①裂隙倾角0°和90°的煤体试件，在整个试件的接触力呈现红色的高应力密集斑点状分布、无明显的应力集中，说明颗粒之间的接触力整体处于较高的水平。②裂隙倾角15°裂隙的煤体试件，整体接触力呈现绿色分布、红色高应力的斑点密度明显降低、无明显应力集中，颗粒之间的接触力整体低于0°和90°的试件颗粒之间的接触力。③倾角30°的试件，由于预制裂隙两端产生的次生裂隙沿加载方向扩展发育至上下边界，裂隙扩展后使两侧原有的接触连接断裂，在扩展裂隙的内侧产生了纵向空白的颗粒之间无接触力区域，在预制裂隙末端产生了明显的应力集中，试件整体应力水平较低。④裂隙倾角45°和60°试件，预制裂隙两端产生的次生裂隙沿加载方向扩展的长度逐渐变小，在扩展裂隙的内侧产生了一定范围纵向空白的颗粒之间无接触力区域，该区域随倾角的增加逐渐减小，试件整体应力水平高于30°的试件。⑤裂隙倾角75°仅在预制裂隙面两侧形成了小范围的无接触力区域，试件在预制裂隙末端和次生裂隙周围形成了红色应力集中区域，其他区域也有较高密度的红色斑点的高应力分布，试件应力水平较高。总体来看，裂隙倾角30°试件由于次生裂隙最长发育到了加载边界，试件整体的应力水平最低、宏观力学性能最差。裂隙倾角由30°向两侧变化，应力传递效果和宏观力学性能逐渐好转，0°和90°整体应力水平最高、宏观力学性能最强。

图7 不同裂隙倾角煤体试件接触力分布Fig.7 Contact force distribution of coal specimens with different fissure type

共面断续双裂隙和非共面平行双裂隙两类试件随裂隙倾角的变化规律与单裂隙的类似。共面断续双裂隙试件在裂隙之间产生了红色的应力集中区域，白色的无接触应力的区域较单裂隙的明显减少，应力水平和宏观力学性能强于单裂隙试件。非共面平行双裂隙试件，由于预制裂隙在加载方向存在一定范围的重叠，白色的无接触应力的区域较单裂隙的明显增多，应力水平和宏观力学性能弱于单裂隙试件。因此，从不同裂隙类型来看，相同裂隙倾角下的不同裂隙类型的整体应力的大小关系相同：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件。细观的接触力的分布情况，进一步揭示了宏观力学参数受裂隙影响的内在本质。

4 含裂隙煤体能量积聚、耗散特征及冲击倾向性分析

4.1 含裂隙煤体能量积聚、耗散特征

4.1.1 不同裂隙煤体试件的弹性应变能分布特征

加载作用下，煤体的原始裂隙经过扩展、汇集、贯通、成核等过程直至完全失稳破坏，原始裂隙演化过程伴随着能量的转移和释放。因此，研究单轴压缩条件下不同裂隙的演化过程的能量耗散机制，有助于揭示裂隙煤体冲击破坏特征的内在本质。

图8 和图9 给出了完整试件和不同裂隙类型试件加载到峰值强度时的弹性应变能分布。受到裂隙的影响，含裂隙试件的弹性应变能密度明显低于完整试件，裂隙削弱了煤岩体储存能量的能力。图9a为单裂隙试件不同倾角的弹性应变能分布图。对于0°和90°倾角的裂隙试件，在试件表面形成不均匀的红色斑点状高能量区域，试件整体的弹性应变能密度高于其他倾角的试件，说明积聚了较高弹性应变能。对于15°倾角的裂隙试件，在试件表面形成不均匀的红色斑点状高能量区域，但不均匀红色斑点高应变能的分布密度较0°和90°倾角的裂隙试件低，试件整体的聚的弹性应变能低于0°和90°。对应30°倾角的裂隙试件，在预制裂隙两端产生的次生裂隙达到了上下边界，在两贯穿裂隙的内侧积聚的弹性应变能量值很低形成了低能量区，在两贯穿裂隙的外侧积聚的弹性应变能量值较高形成了高能量区，在裂隙端部能量集中区。裂隙倾角从30°～75°变化，随着裂隙倾角的增加，次生裂隙长度逐渐变短，低能量区的范围逐渐减小，高能量区的范围逐渐增多，裂隙倾角75°时仅形成了很小范围的低弹性应变能区。从弹性应变能的分布情况来看，随着裂隙倾角的增大，弹性应变能先减小后增大，裂隙倾角30°时最小，裂隙倾角0°和90°积聚的应变能相对较高，裂隙倾角30°积聚的应变能最低。

图8 无裂隙煤体试件表面弹性应变能分布Fig.8 Distribution of elastic strain energy on surface of coal specimens with no fissure

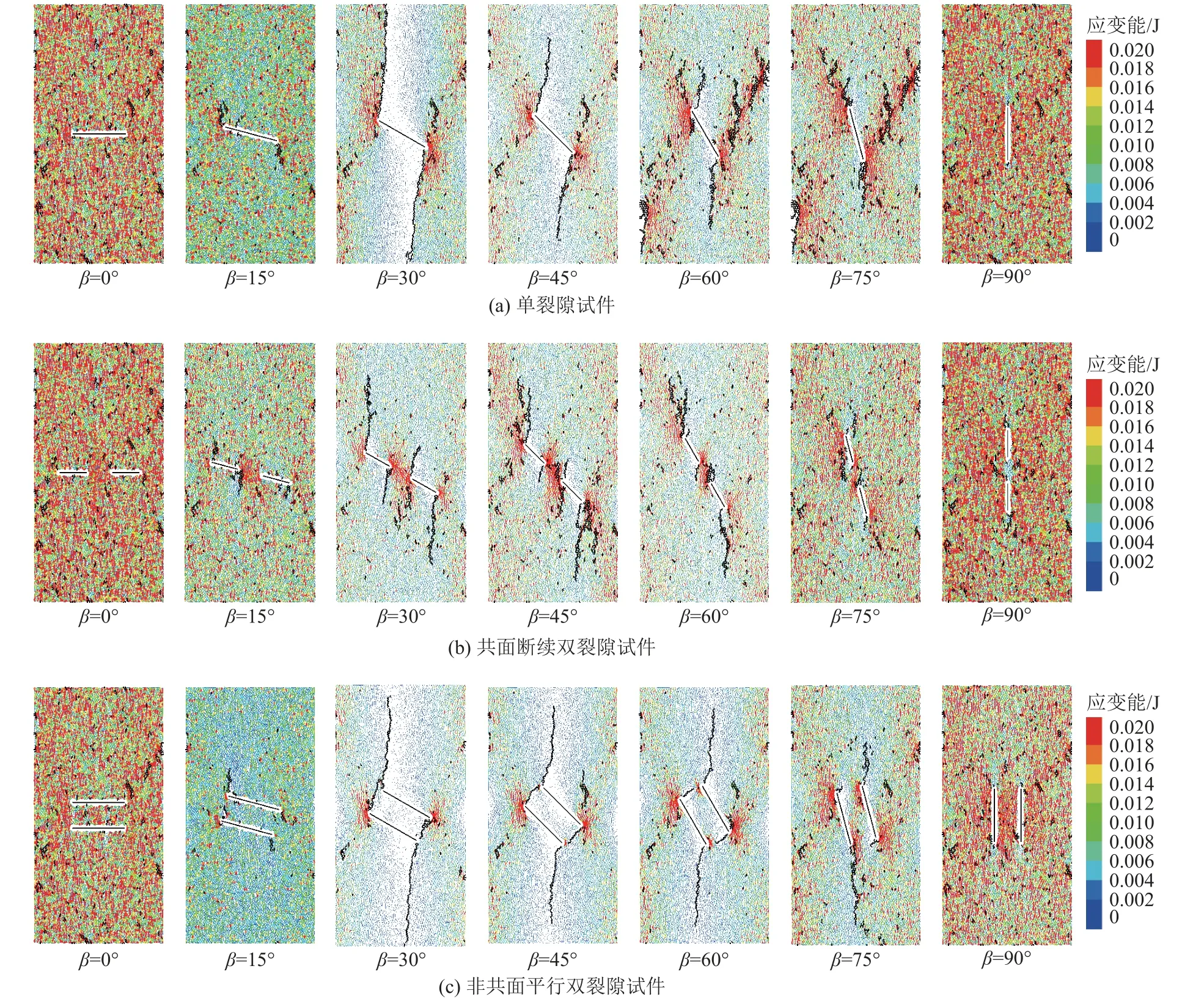
图9 不同裂隙类型煤体试件表面弹性应变能分布Fig.9 Distribution of elastic strain energy on surface of coal specimens with different fissure types

共面双裂隙试件和非共面双裂隙试件弹性应变能分布情况随倾角的变化规律相似。对应裂隙倾角0°和90°的3 组试件，从弹性应变能分布来看差别不明显。如图10 所示，对其他倾角的试件对比后发现：共面断续双裂隙试件，在预制裂隙之间形成了能量集中区、裂隙加载方向的低能量区的范围更小，弹性应变能更高；非共面平行双裂隙试件，在两预制裂隙之间形成了强度相对较低的能量耗散区，使其沿加载方向形成了更大范围的低弹性应变能区域，弹性应变能量更低。因此，各类型裂隙煤体试件积聚弹性能的大小关系为：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件。

图10 不同裂隙类型试件的能量分布特征 (β=45°)Fig.10 Comparison of energy distribution characteristics for different type fissured specimens (β=45° )

4.1.2 不同裂隙类型煤体试件的能量积聚与耗散特征

峰值点弹性应变能代表了岩体的储能极限，反映了岩体抵抗破坏的能力。假定单轴压缩试验环境与外界不存在热交换效应，忽略岩块弹射而转化的动能，则试验机对试件做的功总输入能量为U。根据热力学第一定律，岩石吸收的总应变能U转化为可释放的弹性应变能Ue被储存在试件内以及用于损伤扩展消耗掉的耗散应变能Up。可以得到单轴压缩过程中应变能，见式(1)：

式中：U、Ue和Up分别为峰值点处总应变能、弹性应变能和耗散应变能。单轴压缩加载中试件的弹性应变能Ue与耗散应变能Up之间的关系如图11 所示。

图11 基于应力-应变曲线的能量关系示意Fig.11 Schematic of energy relationship based on stress-strain curve

采用PFC 数值模拟方法，根据式(1)对不同裂隙类型煤体试件在峰值点处卸荷，进而计算得到弹性应变能Ue和耗散应变能Up。表1 给出了不同裂隙类型应力峰值点处总应变能、弹性应变能和耗散能，由表2 可知：含裂隙煤体试件的总应变能和弹性应变能随裂隙倾角的变化均呈现先减后增的变化规律；当裂隙倾角从0°增大至30°时，裂隙煤体峰值点处弹性应变能和总应变能逐渐减小；当裂隙倾角从30°增大至90°时，裂隙煤体峰值点处弹性应变能和总应变能逐渐升高。从不同类型裂隙的能量对比来看，储存能量的大小关系为：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件，这与表面应变能分析的结果相一致。

表2 不同裂隙类型试件峰值点处能量耗散特征Table 2 Characteristics of energy dissipation at peak point of specimens with different fissure types

4.2 含裂隙煤样冲击倾向特征

上述分析可知，由于不同裂隙的煤体试件破坏过程中裂隙作用方式的差异，导致能量的积聚、耗散和峰值应变的大小存在明显不同。同时，由图5 可看出，裂隙不仅改变了原始煤体的能量分布和储存能量的能力，而且使得与煤岩体脆性冲击破坏密切相关的应变值存在明显差异。因此，有必要将能量和应变考虑进去，从能量储存和释放的角度对裂隙煤体的冲击倾向性进行深入分析。

4.2.1 冲击倾向性指标的提出

目前，冲击倾向性指标主要包括强度指标、刚度指标、变形指标和时间指标等，这些指标均可在一定程度上反应试件峰前弹性能量积累或破坏后能量消耗或二者相对关系。因此，从煤岩体储存弹性能的能力和破坏后释放弹性能的能力2 个角度对冲击倾向性进行分析。

煤岩体储存弹性能的能力可用弹性能存储率来衡量。弹性能存储率可定义为单位应变储存的弹性应变能，即应力达到峰值时储存的弹性应变能与峰值应变的比值。如图12 所示2 种应力应变曲线峰值前储存的弹性能相同，按照常规的最大储存弹性应变能指数来判定二者的冲击倾向性相同。曲线1的斜率较小，在较大的应变条件下才达到该能量值；而曲线2 的斜率较大，在较小的应变条件下就达到了该能量值，单位应变储存的能量更高，该种试件更易储存弹性能。在相同的能量条件下，发生很小的应变，煤岩体就会将全部弹性能释放出来，具有明显的脆性破坏特征；而变形较大，煤岩体就会将弹性应变能缓慢释放出来，具有明显的塑性破坏特征。因此，弹性能存储率越高，越有利于弹性能的积累，煤岩体的破坏更为剧烈而具有更强的冲击倾向性。

图12 相同储存弹性能的条件下不同峰值应变的应力-应变曲线对比Fig.12 Comparison of stress-strain curves of different peak strains under same stored elastic energy

煤岩体破坏后释放弹性能的能力可用弹性能释放率来衡量。峰前弹性能量积累与峰后能量消耗之差，是造成煤体冲击破坏的有效能量来源。弹性能释放率可定义为单位应变释放的弹性能，即峰前弹性能量积累与峰后能量消耗之差与完全破坏累计应变的比值。在释放能量相同的情况下，累计应变越小，单位应变释放的能量就越多即弹性能释放率越高，冲击倾向性越强，破坏更为强烈。

弹性能存储率(Elastic Strain Energy Storage Rate,ESESR)和弹性能释放率(Elastic Strain Energy Release Rate,ESERR)的计算公式如下：

式中：Ue和Ua分别为应力峰值处所储存的弹性应变能和应力峰值后消耗的弹性应变能；εc和 εf分别为应力峰值处的应变和试件完全破坏累计的应变。

冲击地压的发生与能量的储存、释放都是密切相关的。储能的能量是冲击地压发生的基础，弹性能存储率越高，煤岩体更易积聚能量。在积聚大量能量的前提下，弹性能释放的能力即弹性能释放率的大小是冲击倾向性强弱的关键。

4.2.2 含裂隙煤体冲击倾向性规律分析

根据前文论述的冲击倾向性指标的评价方法，从煤体储存和释放能量的角度对裂隙煤体冲击倾向性进行分析。如图13 所示，计算得到不同裂隙试件的弹性能储存率和弹性能释放率。弹性能储存率和弹性能释放率标均呈现先降低后升高的变化趋势，裂隙倾角30°的试件两指标最低。从不同裂隙类型对比分析可知，不同裂隙类型煤体试件冲击倾向性的大小关系为：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件。裂隙冲击倾向性的变化规律与上述的宏细观力学特性和能量积聚特性相一致。

图13 不同裂隙类型煤体试件的冲击倾向性对比Fig.13 Comparison of coal burst tendency of coal specimens with different fracture types

综上所述，裂隙对煤体的力学特性、能量积聚耗散特征和冲击倾向性具有重要影响。对矿井冲击地压的防治具有一定指导意义，具体分析如下：

1) 裂隙角度的影响。裂隙倾角为30°时，由于裂隙沿加载方向最容易扩展，裂隙扩展后使两侧原有的接触连接断裂，在扩展裂隙的内侧为低应力区，试件积累能量程度相对较低，冲击倾向性最弱。而0°和90°裂隙的煤体，在加载过程中，应力和能量均处于较高的水平。因此，在相同裂隙密度条件下，煤体裂隙倾角30°时，冲击倾向性最弱，有利于降低冲击地压危险；而倾角向两侧变化冲击倾向性逐渐增强，煤体裂隙倾角0°和90°时，冲击倾向性最强，不利于冲击地压的防治。

2) 裂隙分布的影响。对于共面断续的裂隙，由于裂隙之间存在应力集中和能量积聚，与连续的裂隙相比具有更强的力学特性和储存能量的能力，冲击倾向性更强。对于平行非共面的裂隙，由于裂隙之间相互重叠，裂隙之间形成了低应力区域和能量耗散结构，与单一裂隙相比具有相对较弱的力学特性和存储能量的能力，冲击倾向性更弱。因此，对于相同倾角和裂隙密度的煤岩体，断续分布的裂隙越多，冲击倾向性更强；而裂隙之间平行分布的越多，煤体整体的冲击倾向性更弱，有利于冲击地压的防治。

5 结 论

1)裂隙倾角对的宏观力学参数的影响为：随着裂隙倾角的增大，抗压强度和弹性模量均表现为先减小后增大的趋势；当裂隙倾角为30°时，两者都取得最小值。不同裂隙类型宏观力学参数大小关系为：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件。对比分析了试件表面接触力的分布情况，进一步揭示了宏观力学参数受裂隙影响的内在本质。

2) 通过含裂隙煤体试件应力峰值处的表面应变能分布和能量耗散分析可知：弹性应变能和总应变能的变化规律与宏观力学参数相似。平行非共面的裂隙试件在裂隙之间形成了能量耗散结构，共面断续双裂隙试件裂隙之间形成了能量集中区，揭示了不同裂隙类型弹性能量大小关系的内在原因。

3) 从煤岩体储存弹性能的能力和破坏后释放弹性能的能力2 个角度对冲击倾向性进行分析，提出了弹性能储存率和弹性能释放率2 个冲击倾向性指标。

4) 裂隙倾角对的冲击倾向性的影响为：随着裂隙倾角的增大，弹性能储存率和弹性能释放率均表现为先减小后增大的趋势；当裂隙倾角为30°时，两冲击倾向性指标都取得最小值。不同裂隙类型冲击倾向性大小关系为：非共面平行双裂隙试件＜单裂隙试件＜共面断续双裂隙试件。裂隙的分布形态对煤体的冲击倾向性具有显著影响，在煤岩体的冲击倾向性评价和冲击地压防治中应考虑裂隙这一因素。

5)由于篇幅限制，未给出两参数冲击倾向性等级的判定标准，今后将通过大量冲击倾向性测试的试验数据的归纳总结，结合冲击破坏特征、声发射特征和破碎分型特征，建立该冲击倾向性指标的评判标准。