弧面分度凸轮工作轮廓曲面的反求与构建

史 诺,刘 琼,李 耀

(1.西安航空学院 机械工程学院, 西安 710077; 2.西安航空学院 计算机学院, 西安 710077)

0 引言

凸轮分度机构是一种间歇运动机构,可以分为平行分度凸轮、圆柱分度凸轮,弧面分度凸轮3种类型,主要作用是实现交替的停顿和转动。凸轮分度机构可以应用在供弹装置中,例如外能源自动机通过平行分度凸轮机构或圆柱分度凸轮机构协调拨弹轮持续运动与进弹轮间歇运动之间的关系,在发射炮弹的安全性、精准性方面发挥着重要作用[1-3]。凸轮分度机构还可以应用在弹药生产中,在弹药连续引申成形过程中,利用弧面分度凸轮分时控制弹药部件的送料量,能够有效提高生产效率[4]。相比于平行分度凸轮、圆柱分度凸轮,弧面分度凸轮的刚性强、工作转速高、且能够承受重载[5-7],在兵器装备领域的应用前景广阔。

弧面分度凸轮工作轮廓曲面形式较为复杂,是不可展开的空间曲面,设计难度较大。采用现代数字化设计工具建立弧面分度凸轮的工作轮廓曲面主要有2种方法:一种是利用编程软件计算工作轮廓曲面的坐标点,形成数据点集,然后导入三维设计软件中,逐步生成曲线、曲面[8-9],简称为“点—线—面”法,这种方法的编程工作量较大,数据点集的规模决定了曲面精度;另一种是根据工作轮廓曲面方程,在三维设计软件中绘制出若干条轮廓曲线,然后通过曲线组生成曲面[10-11],简称为直接建模法,这种方法的作图过程较为繁琐,设计周期较长。

弧面分度凸轮的工作轮廓曲面与分度盘的滚子曲面之间一直保持无间隙的相切接触关系,是一对共轭曲面。从接触形态上来讲,两者呈现垂直啮合状态,本文根据空间共轭理论推导工作轮廓曲面数学模型,在此基础上,分析弧面分度凸轮与分度盘的相对运动关系,通过分度盘的运动规律反求弧面分度凸轮的工作轮廓曲面,旨在避免复杂的编程计算,简化作图过程,高效精确的构建工作轮廓曲面,为弧面分度凸轮的制造与应用提供技术支撑。

1 工作轮廓曲面的数学模型

建立弧面分度凸轮的坐标系统,如图1所示,分别在分度盘中心、弧面分度凸轮中心建立固定坐标系H0—o0x0y0z0、H3—o3x3y3z3,其中z0轴、z3轴为分度盘、弧面分度凸轮的中心轴线,x0轴由分度盘中心指向弧面分度凸轮中心,x3轴的方向与x0轴保持一致;y0轴、y3轴的方向按照右手定则进行确定。除了上述两个固定坐标系外,在弧面分度凸轮中心建立与其固连的运动坐标系H1—o1x1y1z1,在分度盘中心建立与其固连的运动坐标系H2—o2x2y2z2。

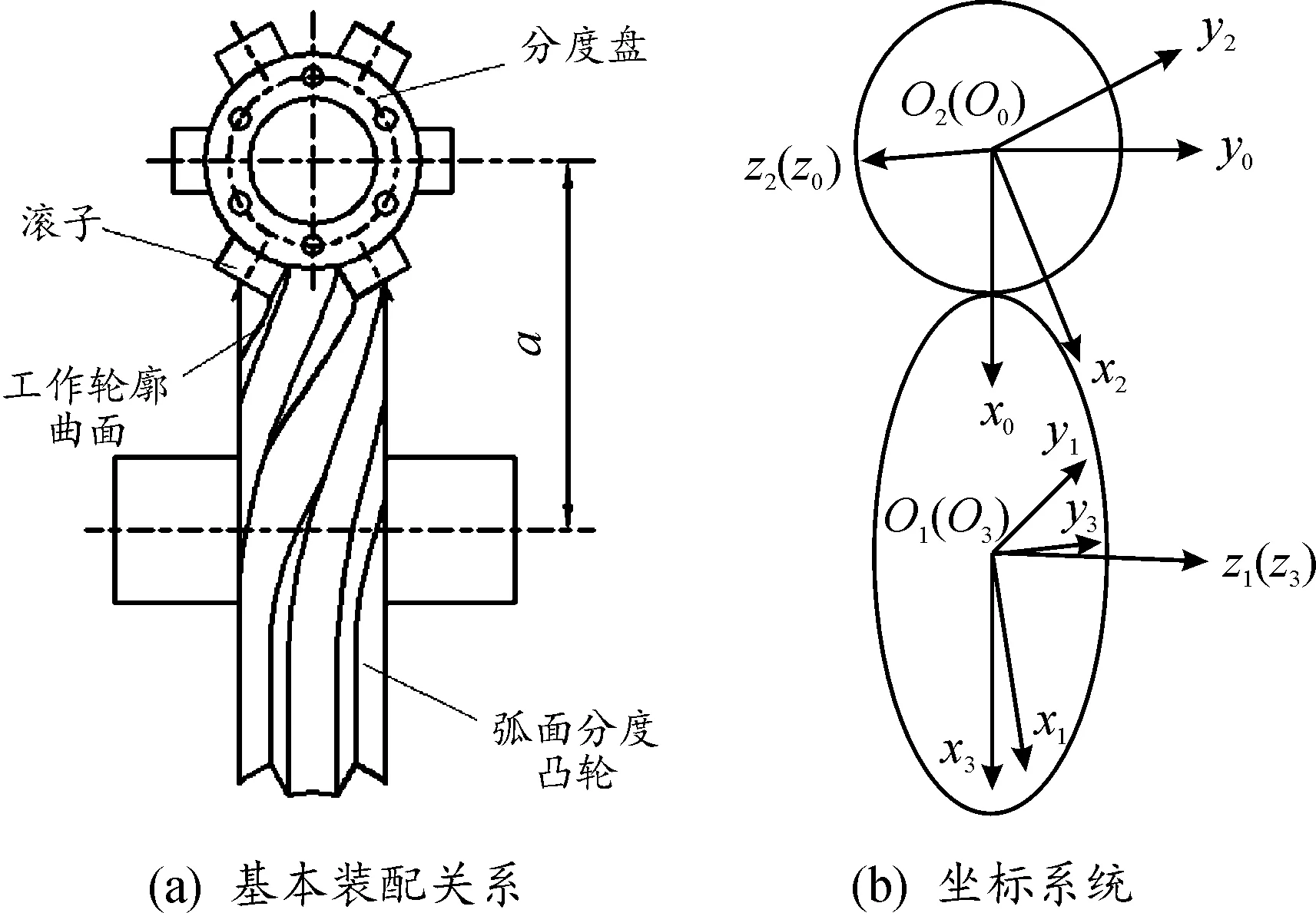
图1 弧面分度凸轮机构Fig.1 Globoidal indexing cam mechanism

如图2所示,θ1为滚子的位置角,将坐标系H2—o2x2y2z2绕z0轴旋转θ1角度后得到坐标系H0—o0x0y0z0,2个坐标之间的转换矩阵H02为:

图2 坐标系H2与H0的转换关系Fig.2 Transformation relationship between coordinate system H2 and H0

(1)

如图3所示,将坐标系H0—o0x0y0z0首先做关于x0o0y0平面的对称变换,然后将y0轴、z0轴进行互换,最后平移中心距a的距离,得到坐标系H3—o3x3y3z3,2个坐标之间的转换矩阵H30为:

图3 坐标系H0与H3的转换关系Fig.3 Transformation relationship between coordinate system H0 and H3

(2)

则坐标系H2—o2x2y2z2与H3—o3x3y3z3之间的转换矩阵H32可以表示为:

H32=H30·H02=

(3)

如图4所示,θ2为弧面分度凸轮的转角,将坐标系H3—o3x3y3z3绕z3轴旋转θ2角度后得到坐标系H1—o1x1y1z1,2个坐标之间的转换矩阵H13为:

图4 坐标系H3与H1的转换关系Fig.4 Transformation relationship between coordinate system H3 and H1

(4)

则坐标系H2—o2x2y2z2与H1—o1x1y1z1之间的转换矩阵H12可以表示为:

H12=H13·H32=

(5)

假设滚子上接触点为Q,其坐标为(x2,y2,z2),由于两曲面共轭接触位置上的接触点是重合的,将Q点的坐标从坐标系H2—o2x2y2z2变换到H1—o1x1y1z1中,得到弧面分度凸轮上共轭接触点坐标,将滚子曲面上所有共轭接触点集合进行变换,即可得到弧面分度凸轮的工作轮廓曲面方程为:

(6)

考虑到凸轮的旋向问题,其工作轮廓曲面的数学模型为:

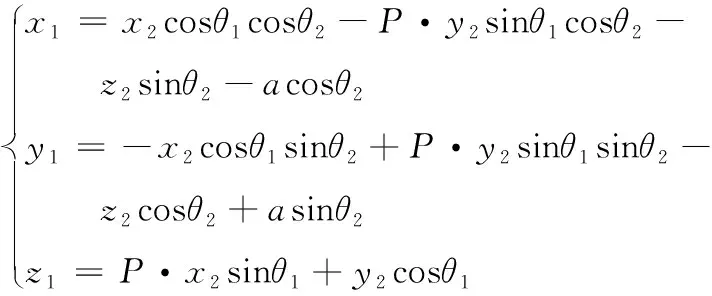
(7)

式中:P为旋向系数,左旋时取值为1、右旋时取值为-1。

由式(7)可知,建立工作轮廓曲面需要有两个必要条件,一是明确滚子与凸轮的转角变化规律,即机构的共轭运动规律;二是需要确定滚子的曲面方程,由于分度盘的滚子常采用圆柱形状,形式较为简单,确定滚子的结构参数即可。

2 工作轮廓曲面的创建

2.1 基础参数的确定

2.1.1运动规律的选择

设定弧面分度凸轮的分度期转角为120°,停歇期转角为240°;分度盘分度期转角为2个相邻滚子之间的夹角,设置为60°,停歇期转角为0°;分度盘分度期运动规律直接影响着机构的运行精度,常见的运动规律有等速、等加速等减速、五次多项式、简谐(余弦加速度)、摆线(正弦加速度)、改进正弦加速度等类型[12],对各种运动规律的特性参数进行计算,遵循速度、加速度及跃度的最大值尽可能较小原则[13],以及运动特性参数曲线连续性原则选择合理类型。改进正弦加速度的运动特性参数如下所示:

分度期初始阶段:

(8)

分度期中间阶段:

(9)

分度期终末阶段:

(10)

式中:T为无量纲周期;S为无量纲位移;V为无量纲速度;A为无量纲加速度;J为无量纲跃度。

通过定量计算与综合比较,改进正弦加速度的运行特性较为优良,其冲击和振动小[14],能够实现精确步进,适用于高速重载场合,本文设计中的分度盘分度期采用改进正弦加速度运动规律。

2.1.2结构参数的计算

弧面分度凸轮的旋向大多采用左旋形式,对其结构参数进行计算,具体过程不再赘述,其主要结构参数见表1,根据结构参数在UGNX的建模环境下创建凸轮毛坯、分度盘两个元件的三维模型并进行装配,如图5所示。

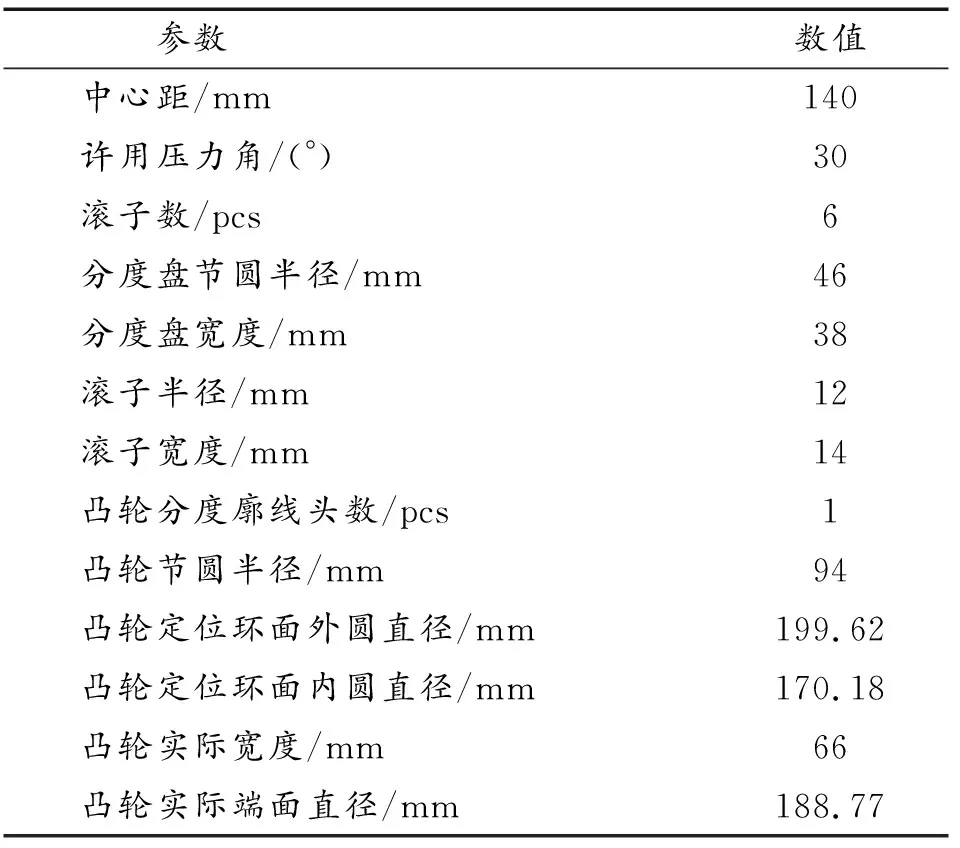
表1 主要结构参数Table 1 Mainstructural parameters

图5 凸轮毛坯与分度盘的装配模型Fig.5 Assembly of cam blank and indexing plate

2.2 理论工作轮廓曲面的获取

2.2.1生成原理

弧面分度凸轮机构是通过工作轮廓曲面与滚子曲面的啮合将连续的匀速回转运动转化为间歇转动,在图5所示的机构中凸轮毛坯进行匀速回转运动,分度盘以改进正弦加速度运动规律进行间歇转动。对整个机构施加附加转动,该转动与凸轮毛坯的匀速回转运动大小相同、方向相反,则凸轮毛坯固定不动,滚子进行复合运动,在绕凸轮毛坯中心轴线匀速公转的同时,以改进正弦加速度的运动规律绕分度盘中心轴线自转,圆柱滚子中心轴线在复合运动的过程中形成的曲面即为弧面分度凸轮的理论工作轮廓曲面。

2.2.2曲面反求

根据曲面生成原理,从分度盘的复合运动反求工作轮廓曲面。将凸轮毛坯与分度盘的装配体切换到运动仿真环境下,依据设置运动体—定义运动副—施加驱动的步骤开展计算。设置凸轮毛坯、分度盘、分度盘中心轴线为运动体;在凸轮毛坯上定义固定副,分度盘中心轴线上定义接地旋转副,其旋转中心为凸轮毛坯中心轴线,分度盘以及分度盘中心轴线之间定义相对旋转副;在接地旋转副上添加驱动1,使分度盘匀速公转,在相对旋转副上添加驱动2,使分度盘遵循改进正弦加速度运动规律自转,假设在0～1 s内,分度盘转动60°,弧面凸轮转动120°;在1～3 s内,分度盘停止转动,弧面凸轮转动240°,采用角位移的形式计算驱动1、驱动2,结果如表2所示。

表2 驱动参数Table 2 Driving parameters

采用电子表格的方式施加驱动1与驱动2,将圆柱滚子中心轴线的2个端点进行标记,在机构的运动过程中对标记点进行追踪,得到的追踪轨迹如图6所示。

图6 追踪轨迹Fig.6 Pursuit tracking

将整个模型切换到建模模块,将追踪轨迹1、追踪轨迹2生成样条曲线,并通过这2条样条曲线创建曲面,得到的理论工作轮廓曲面如图7所示,其中分度曲面段为分度期工作曲面,定位环面段为停歇期工作曲面。

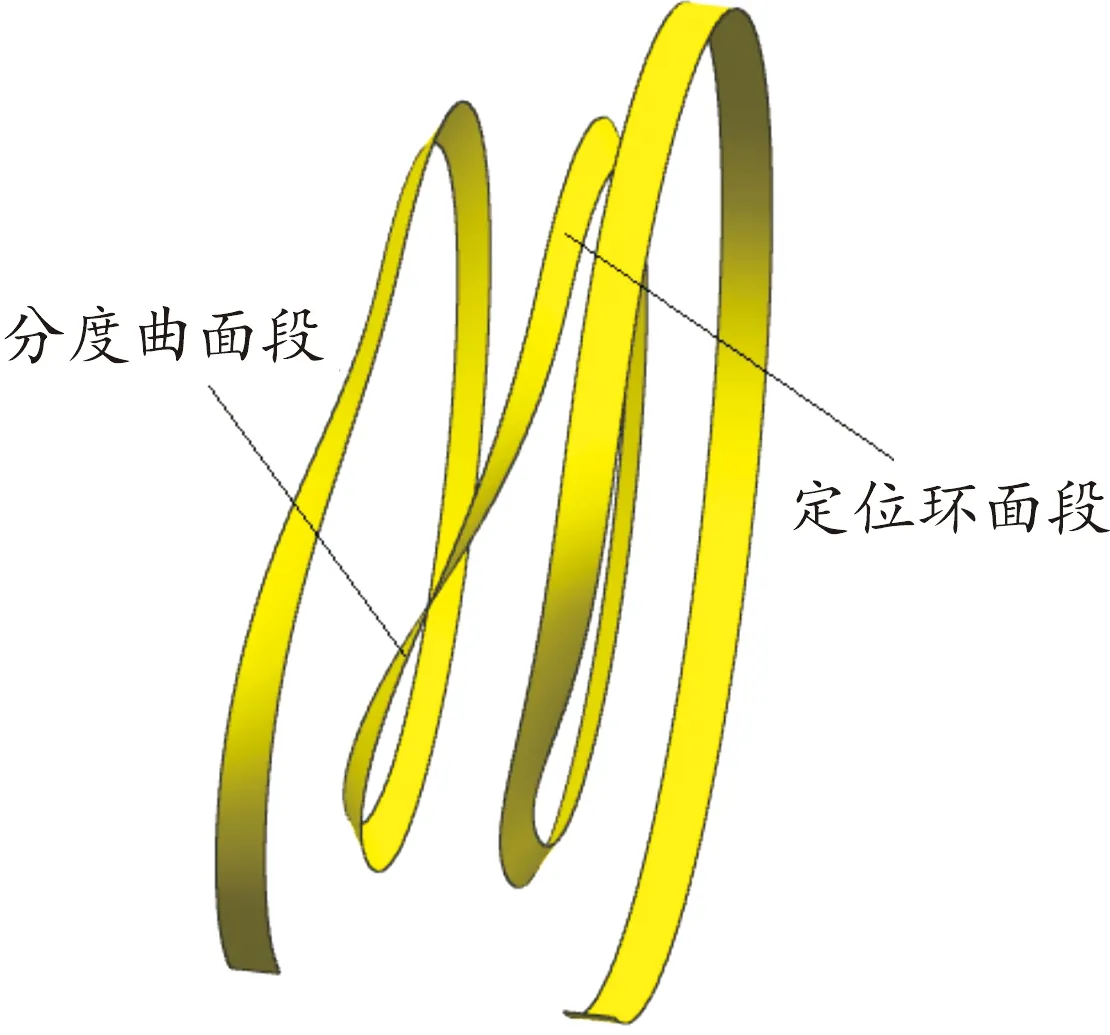
图7 理论工作轮廓曲面Fig.7 Theoretical working profile surface

2.2.3光顺度检查

分度曲面段与定位环面段的光顺度直接决定着分度盘运动的平稳性,如图8所示,对整个理论工作轮廓曲面进行表面反射斑马线检查,特别对分度曲面段与定位环面段之间的过渡部分进行放大观察,可以发现,整个曲面上的斑马线是连续的,说明理论工作轮廓曲面质量良好,表面质量符合工业要求。

图8 曲面光顺度检查Fig.8 Inspection of surface smoothness

3 仿真验证

将理论工作轮廓面进行双侧加厚,单侧加厚距离与滚子半径相同,将曲面加厚后形成的实体与凸轮毛坯进行布尔运算,获得弧面分度凸轮的数字化模型,将分度盘与弧面分度凸轮进行装配,得到弧面分度凸轮机构的三维模型,如图9所示。

图9 弧面分度凸轮机构的三维模型Fig.9 Three-dimensional model of globoidal indexing cam mechanism

对整个机构进行运动仿真,输出分度盘的角位移、角速度、角加速度进行分析,以验证工作轮廓曲面的准确性。机构中各零件的运动关系可以分为两类:旋转与共轭接触,故在弧面分度凸轮、分度盘的中心轴线处分别设置接地旋转副,在弧面分度凸轮的工作轮廓曲面与分度盘滚子曲面直接设置3D接触,对弧面分度凸轮施加120(°)/s的恒定转速,假设整个机构工作时间为6 s。

分度盘的角位移变化曲线如图10所示,可以明显观察到,机构运行了2个周期,分度期角位移剧烈变化,间歇期角位移基本恒定不变,每个周期的角位移为60.184 7°,与设计值60°的误差值为0.307 8%,处于合理范围之内,整体来看,角位移变化规律的仿真结果与理论情况相符。

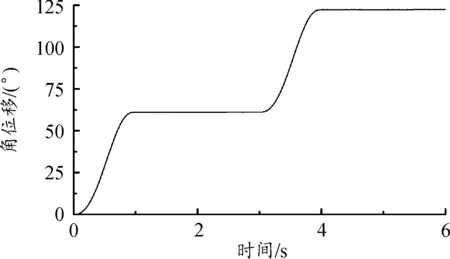
图10 角位移变化曲线Fig.10 Angular displacement curve

分度盘的角速度变化曲线如图11所示,分度期角速度先是急剧上升,在0.51 s附近时,角速度达到了最大值106.153 0(°)/s,然后迅速下降,间歇期角速度基本保持为0(°)/s。改进正弦加速度运动规律的无量纲最大角速度为:

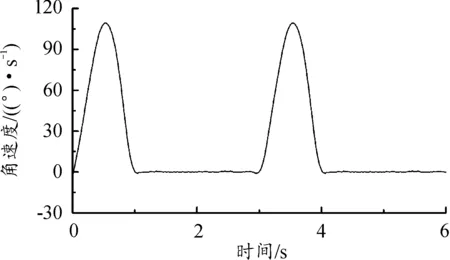
图11 角速度变化曲线Fig.11 Angular velocity curve

(11)

式中:θf为弧面分度凸轮转角;φf为分度盘分度期转角;ω1为弧面分度凸轮角速度;ωmax为分度盘最大角速度。则仿真运动中:

(12)

已知改进正弦加速度运动规律的理论最大角速度为1.76,仿真值与理论值的误差为0.522 7%,吻合度较好。

分度盘角加速度变化曲线如图12所示,在整个过程中角加速度曲线呈现振荡状态,主要是由2个原因造成的,一是分度盘上的滚子曲面与弧面分度凸轮中的工作轮廓曲面之间存在刚性碰撞,在实际工作中,可以通过良好的润滑来起到缓冲和减振的作用[15];二是工作轮廓曲面存在一定的精度误差,可以通过密化追踪点的数量来提高模型质量。从其中还可以看到,在2个分度期内,角加速度变化趋势与正弦加速度运动规律的特点相符合,在0.87 s附近时,角加速度达到最大值388.189 6(°)/s2,改进正弦加速度运动规律的无量纲最大角速度为:

图12 角加速度变化曲线Fig.12 Angular acceleration curve

(13)

则仿真运动中:

(14)

已知改进正弦加速度运动规律的理论最大角加速度为5.91,仿真值与理论值的误差为9.472 1%,处于允许的偏差范围之内。

从分度盘的角位移、角速度、角加速度的变化趋势及极值来看,弧面分度凸轮的工作轮廓曲面可以满足分度要求,能够实现预期的运动规律。

将本文中提出的反求设计方法与2种常规方法进行对比分析。“点—线—面”法需要将数据点集从编程软件导入三维设计软件当中,坐标数据不可避免的存在舍入误差,而直接建模法只在三维设计软件中进行操作,不存在数据转换问题,因此直接建模法优于“点—线—面”法[16]。在相同的结构参数下,采用直接建模法设计弧面分度凸轮工作轮廓曲面,分度期绘制曲线108条,停歇期绘制曲线18条,共计绘制126条曲线后形成了曲面,而反求设计方法绘制2条曲线就可以生成曲面,设计效率大大提升。对直接建模法设计的弧面分度凸轮机构进行虚拟仿真,每个周期的角位移、角速度最大值、角加速度最大值与理论值的误差分别为0.325 2%、0.592 1%、9.892 6%,直接建模方法的运动精度略低于反求设计方法,这主要是因为直接建模法创建的曲线较多,形成了多处曲面的连接过渡,对于模型质量有一定影响。综上所述,反求设计方法在设计效率和建模精度上均具有一定的优势。

4 结论

1) 以弧面分度凸轮工作轮廓曲面与分度盘滚子曲面之间的共轭接触状态为理论依据,利用空间坐标变换的方法推导了工作轮廓曲面方程,从方程中得到了创建工作轮廓曲面的必要条件,采用运动仿真的技术手段反求曲面,求解过程避免了复杂的程序编制与数值计算,简洁明确。

2) 在弧面分度凸轮分度期转角120°、分度盘6工位、中心距140 mm、分度盘输出运动规律为改进正弦加速度类型的结构条件下,对主动件弧面分度凸轮上施加120(°)/s的恒定转速后进行6 s的仿真计算,计算结果表明从动件分度盘运转了2个周期,且输出的运动特性变化趋势与理论一致,其每个周期的角位移为60.184 7°,与理论值的误差为0.307 8%,角速度最大值为106.153 0(°)/s,与理论值的误差为0.522 7%,角加速度最大值为388.189 6(°)/s2,与理论值的误差为9.472 1%,从运行效果来看,弧面分度凸轮的工作轮廓曲面能够实现功能要求。

3) 基于弧面分度凸轮工作轮廓曲面方程,利用UG NX的运动仿真功能反求工作轮廓曲面,为复杂分段曲面的构建提供了崭新的设计思路与技术路径,具有较为广阔的工程应用前景。