模糊变结构控制策略在UUV航向运动中的应用与分析

周 浩,龙景豪

(海军工程大学, 武汉 430033)

0 引言

在UUV水下行进运动过程中,合理有效的控制策略选取起着至关重要的作用。事实上,UUV在实现预期的运动时,被控对象本身会受到不同性质的扰动,这些扰动包括系统内部运动数学模型的不确定性(包括模型参数的变化、内外因导致的测控信号瞬间突发变化)、系统外部环境的随机干扰(如各类水动力参数随水介质的变化),后者称之为海洋环境噪声,因此为满足当前UUV水下空间运动的精准控制需求,要求航行控制系统在完成航向跟踪基本性能的前提下同时具备一定的抗扰性能,此外UUV水下航行运动的稳定性也是时时刻刻必须关注的重点。

迄今为止,变结构控制的研究已发展成为相对独立的设计策略[7]。在步入智能化应用的时代,变结构控制以响应速度快、对参数变化不灵敏、具有抗扰性等独特的优势,获得了在线性与非线性系统中的广泛应用,由于控制过程中时常发生抖振现象,限制了变结构控制精准而深入的应用。为了使变结构控制能够继续发挥突出的优势,本文中以变结构控制策略设计为基础,针对非线性控制中的抖振现象,提出一种在模糊化控制策略的设计下达到抑制抖振现象,通过Lyapunov函数设计UUV侧向运动变结构控制器及其模糊化控制器来实现UUV快速精准的航向控制,再利用Simulink仿真验证航向跟踪控制性能,并计算分析对比变结构控制策略和其模糊化控制策略下UUV在航行运动中的稳定性与抗扰性。

1 UUV侧向运动模型

为研究分析UUV姿态控制,首先需要建立航行器的坐标系。依据ITTC推荐及SNAME术语体系要求[7],建立以E为原点的定坐标系E-ξηζ,再建立以O为原点的动坐标系O-xyz,如图1所示。

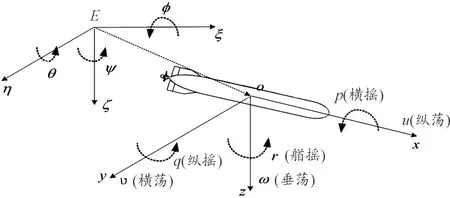
图1 定坐标系和动坐标系Fig.1 Fixed and moving coordinates

定坐标系中,φ、θ和ψ表示航行器的横摇角、纵摇角和艏摇角;ξ、η和ζ表示航行器的位置坐标。动坐标系中,v、q表示航行器的横荡速度、纵摇角速度;ω、p表示航行器的垂荡速度、横摇角速度;u、r表示航行器的纵荡速度、艏摇角速度。

考虑到UUV的6自由度模型较为复杂,为便于UUV航行控制系统的研究分析,可通过解耦获得侧向运动控制和纵向运动控制[8]。本文以侧向运动控制模型为例展开相关研究工作。

UUV侧向运动控制的涵义既包括航行器艏摇运动姿态控制又包括横荡运动姿态控制,最终完成航向角的控制,而控制输入量是UUV推进器作用在垂直舵面上的转矩,将艏摇角速度r、艏摇角ψ和横荡速度v视为被控对象,当横荡速度v为零时,UUV艏摇角等于航向角,将航行器的横荡速度v尽量减小,于是艏摇角可近似看成UUV航向角[9],于是航向跟踪控制可看成对艏摇角速度r、艏摇角误差ψ-ψd以及横荡速度v的跟踪控制。

实际上忽略航行器的垂荡运动、横摇运动与纵摇运动后,航行器的6自由度模型就可以推导得出以下纵荡运动、横荡运动和艏摇运动的动力学方程[10-11]。

(1)

(2)

(3)

式中:m表示航行器质量;F表示航行器螺旋桨推进器提供的纵向推进力;X{·}、Y{·}、N{·}表示航行器的水动力系数;I表示航行器的转动惯量;M表示推进器作用在垂直舵面上的转矩[12]。

为后续验证变结构控制器的实际运用效果,将REMU S100型UUV作为研究分析案例,根据相关文献数据[12],将

Xuu=-1.62 kg/m,Yv|v|=-1 310 kg/m

Yuv=-28.6 kg/m,Yur=-5.22 kg/rad

这些参数标称值用于侧向运动模型,获得数值量化的航行器水平面纵荡运动、横荡运动和艏摇运动的数学模型:

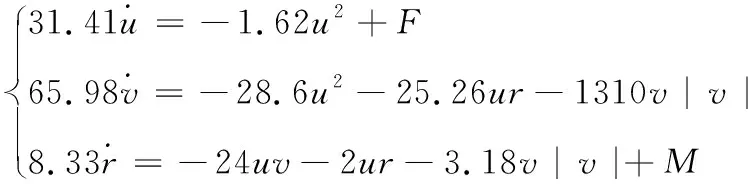
(4)

若将3 m/s的期望纵向速度代入纵荡运动方程,将得到UUV在纵荡方向上的平衡推进力F为14.58 N。由于给定的UUV纵荡速度为常量,于是可将推进力设为常数,得到航行器侧向运动数学模型:

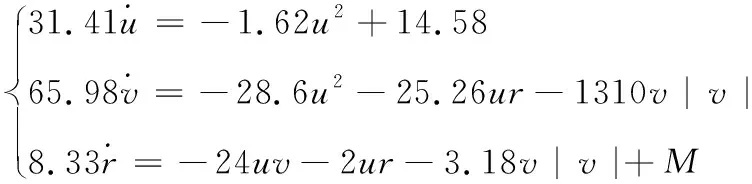
(5)

2 侧向运动控制器设计

2.1 变结构控制器

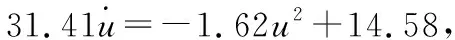
(6)

(7)

之后通过以下步骤完成变结构控制设计:

(8)

2) 定义误差向量

e=[e1e2e3]T,得到:

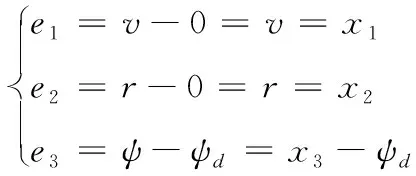
(9)

式中,ψd为期望的UUV艏摇角。

3) 构造变结构控制切换面的函数

s=Ce=c1e1+c2e2+c3e3

(10)

C=[C1C2C3]为常数向量,取为C=[-0.5 0.5 0.7]。

设计变结构控制器时采用常数切换控制律为U=-K·sgn(s),其中K为常数;sgn(·)为符号函数。

2.2 模糊变结构控制器

设V为Lyapunov函数,前提为式(9),所以:

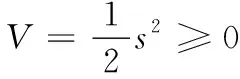
(11)

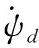
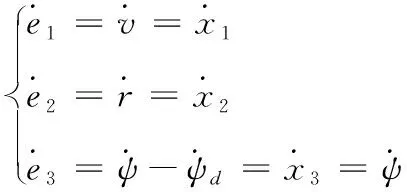
(12)

(13)

对于切换面函数式(10)两边取微分有

(14)

把式(8)、式(12)及U=-K·sgn(s)代入式(14)有

(15)

其中,L=-1.22uv+0.07ur+9.755v|v|+0.7r,H=-30sgn(s),设|u|≤3 m/s,|v|<0.6 m/s,|r|<8.5 rad/s,则有:

|L|=|-1.22uv+0.07ur+9.755v|v|+0.7r|≤

|-1.22uv|+|0.07ur|+|9.755v|v||+|0.7r|=

-1.22|u||v|+0.07|u||r|+9.755|v||v|+

0.7|r|<2.196+1.785+3.511 8+5.95=

13.442 8

(16)

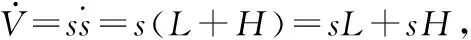
(17)

所以,可以使得UUV渐进跟踪指定的参考航向。

为了获得控制趋近律,用模糊规则取代切换控制律中的符号函数,实现模糊化切换,设计趋近律为U=-K·fuzzy(s),其中K为常数,fuzzy(s)为模糊规则。

假定模糊规则为单输入单输出,于是得到输入论域为A={Ai|NB,NM,NS,ZO,PS,PM,PB},输出论域为B={Bi|NB,NM,NS,ZO,PS,PM,PB},其中NB、NM、NS、ZO、PS、PM、PB分别为模糊语言变量中负大、负中、负小、零、正小、正中、正大,取值范围均为[-3,3]。从而模糊规则为:

IfA=NBthenB=NB; IfA=NMthenB=NM; IfA=NSthenB=NS; IfA=ZOthenB=ZO; IfA=PSthenB=PS; IfA=PMthenB=PM; IfA=PBthenB=PB。

采用加权平均法面积中心法,即

(18)

图2和图3为输入输出隶属函数。

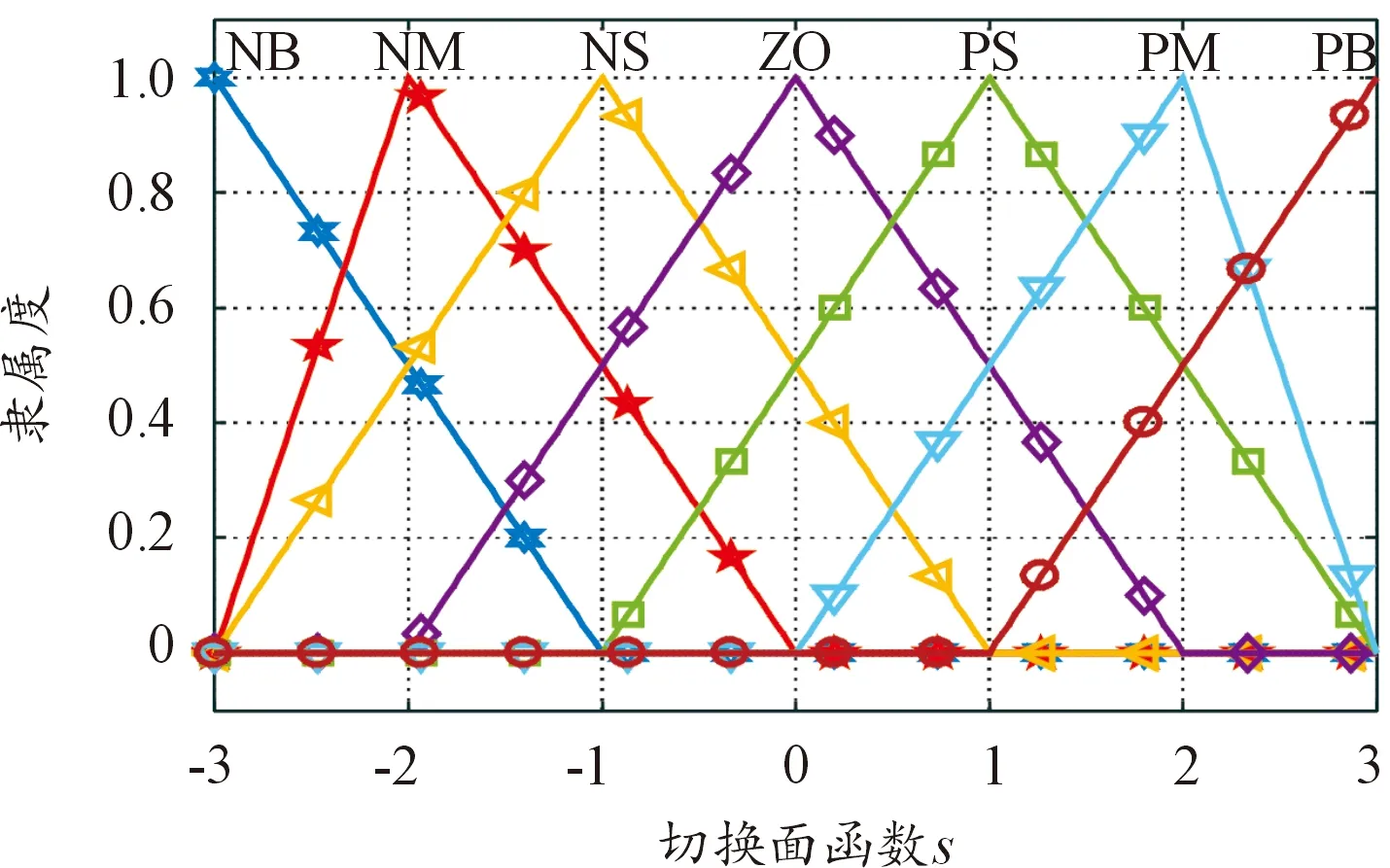
图2 输入的隶属函数Fig.2 Input membership function

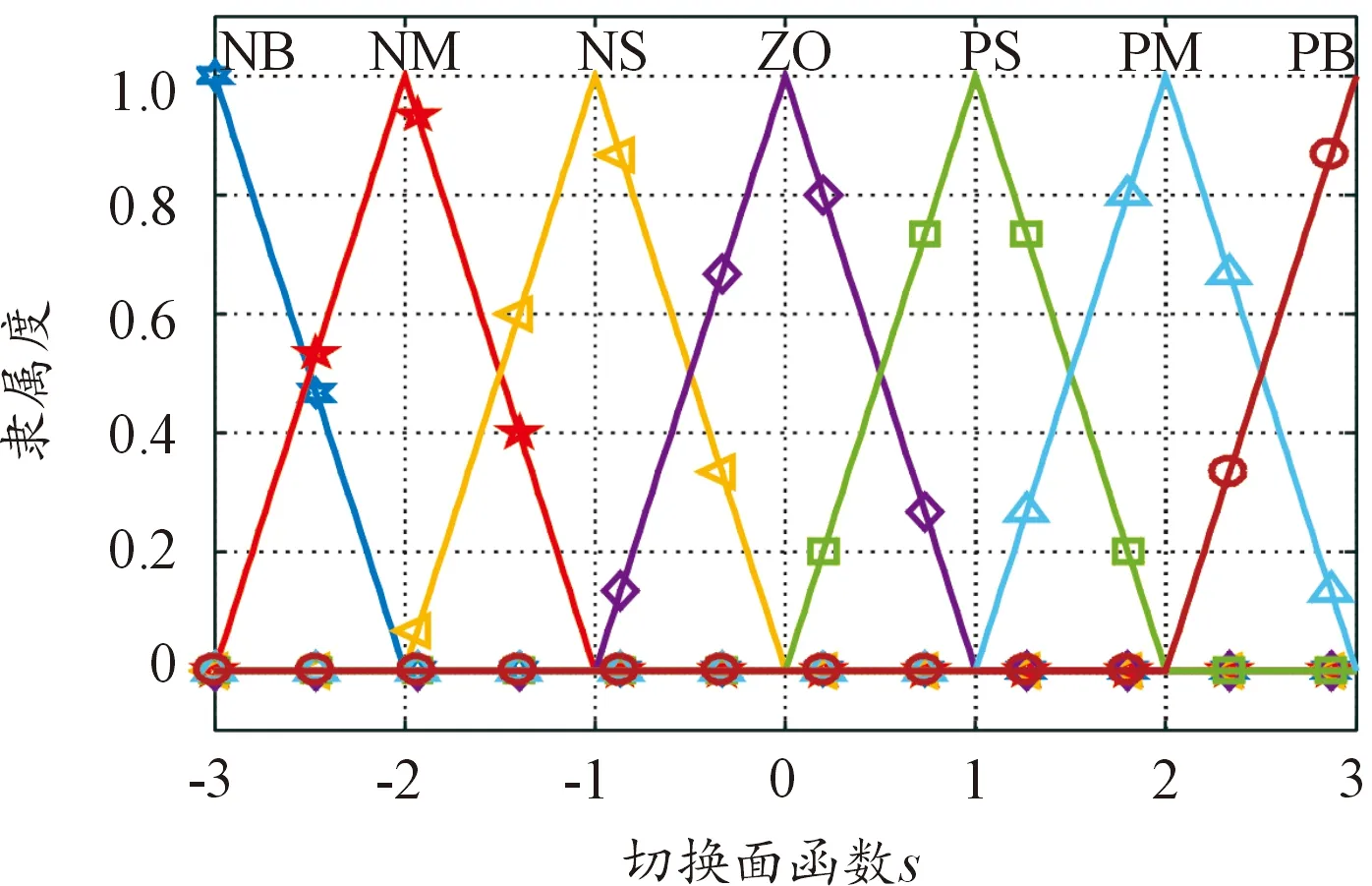
图3 输出的隶属函数Fig.3 Output membership function

3 算例仿真与分析

为考察验证对比变结构控制器和其模糊化控制器在航向跟踪控制方面的性能,本文利用Simulink仿真环境对UUV侧平面姿态控制效果进行相关仿真研究。同时航行器侧向航行控制可看作是在平衡条件下受小幅扰动而进行的小尺度运动,并将REMU S100中的参数作为仿真分析条件。

3.1 Simulink仿真模型构建

在Simulink仿真环境下建立如图4所示的侧向运动控制仿真模型,其中区域1将完成侧向运动模型动力学方程解算,区域2将构造变结构切换面函数,区域3将完成常数切换控制律,其中区域3将进行针对变结构控制中常见的抖振现象完成变结构控制模糊化策略的切换控制律。上述三部分区域(模块)共同形成UUV侧向运动变结构控制构架。

图4 变结构控制下UUV侧向运动控制仿真模型Fig.4 Simulation model of UUV lateral motion control under variable structure control

3.2 航向跟踪性能分析

在阶跃控制输入下,系统切换面函数S与控制量U的时序曲线如图5所示。观察上述曲线能明显看出变结构控制时常出现出现抖振,而模糊化的变结构控制却可以很好地抑制抖振。阶跃控制输入下的UUV艏摇角速度r、横荡速度v的变化曲线如图6所示。显然在阶跃控制输入下,横荡速度v出现小凹槽响应,而在其他时间点上围绕零速作微小尺度的变化,最大幅值低于0.1 m/s,由于前文中提到期望纵荡速度设置为3 m/s,此时将横荡速度与纵荡速度2个不同方向的速度矢量进行合成,经计算合成后的速度矢量与航行器轴向夹角不超过0.033 rad,横荡速度对系统行进姿态的影响基本可忽略,充分表明2种策略控制较好地完成了艏摇角对实际航向角的快速跟踪,实现基本控制目标。而在阶跃控制输入作用后,艏摇角速度响应将在出现一个周期的峰值变化后回归到近似零速状态,表明此时期望航向基本达成。同时仿真结果表明,模糊化控制策略可以很好地抑制变结构控制中发生的抖振现象。

图5 切换面函数与切换控制响应曲线Fig.5 Response curve of switching surface function and switching control

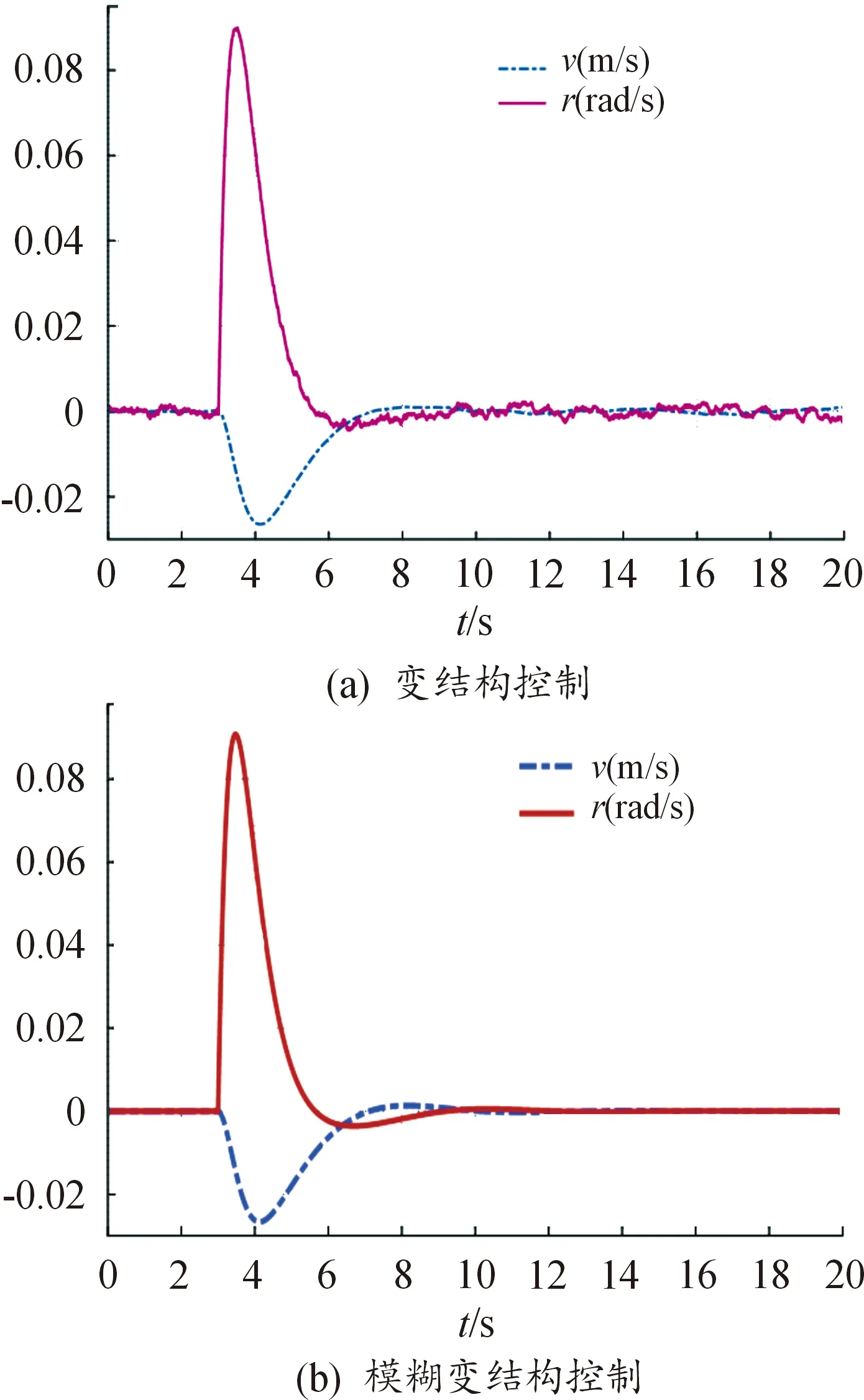
图6 艏摇角速度、横荡速度响应曲线Fig.6 Response curve of bow angular velocity and yaw velocity

上述仿真结果已经说明艏摇角与实际航向角基本趋同,而通过观察艏摇角响应曲线(如图7所示)可以得出:在阶跃控制信号作用于系统后不足3 s的时间内,艏摇角已经与期望输出航向趋于一致,而且超调量较小,稳态误差也不超过0.018 rad,可认为变结构控制较好地完成了目标航向角的控制。结果表明2种控制策略的速度响应曲线整体上相似,而其模糊规则应用的控制策略响应中横荡速度v与艏摇角速度r相对更加地平滑,从而表现出更好的控制效果。

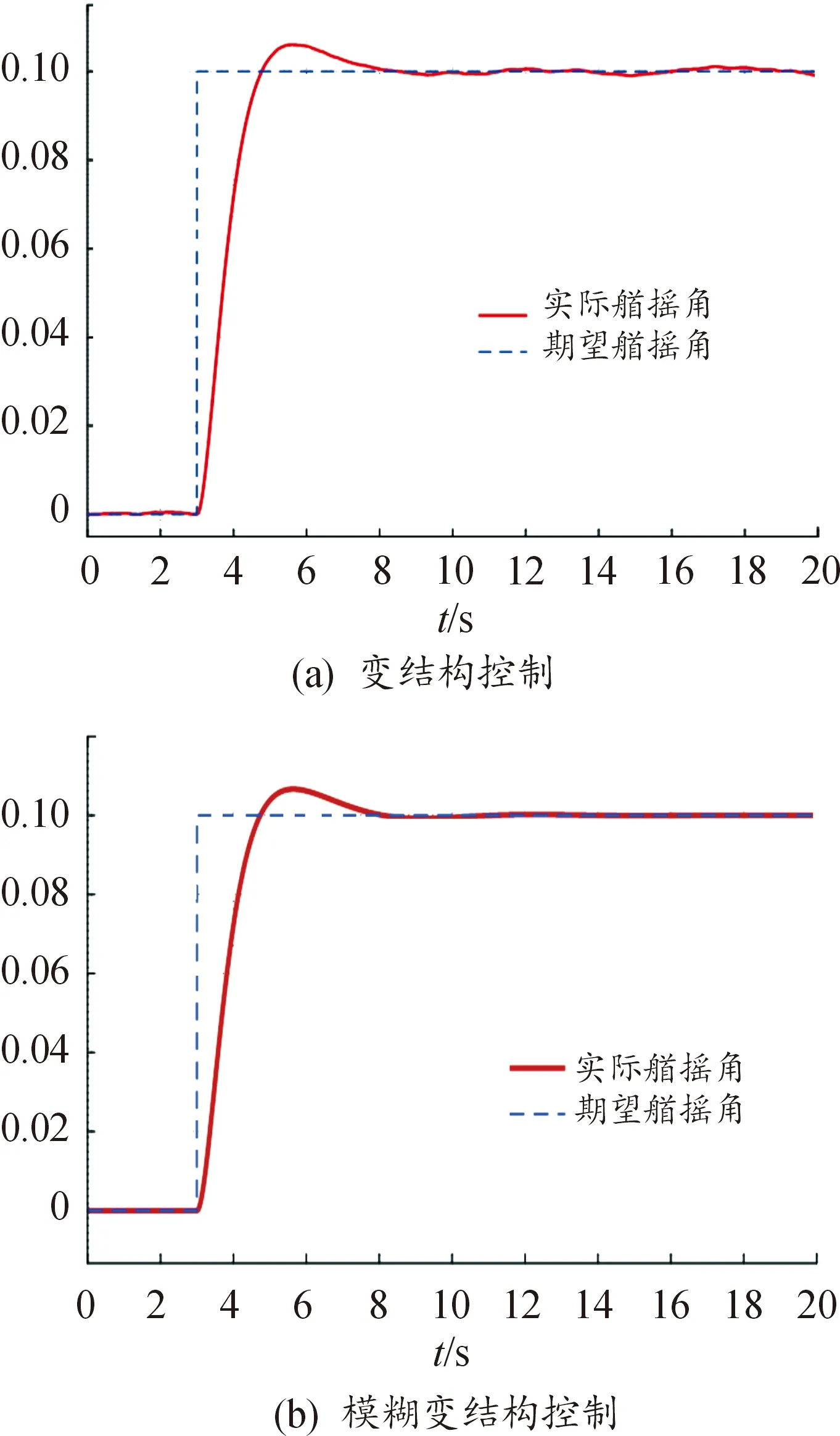
图7 艏摇角响应曲线Fig.7 Bow angle response curve

为了更直观地展示控制策略对UUV侧向运动控制效果,将2种策略控制下侧向运动轨迹以时间为变参量清晰表示,于是在图4模型的基础上增设运动轨迹仿真模型,通过仿真运行,获得航向运动轨迹,通过截图获得如图8所示的组图,仿真中使用阶跃控制信号输入,在3 s输入指令时开始转向到期望航向,在9 s输入指令时开始在转向到期望航向,在15 s输入指令时开始转向期望航向,轨迹图的坐标单位为m。因此,设计的2种策略控制能使UUV侧向运动控制获得较为满意的实际效果。同样模糊化控制策略响应更加平滑,显然控制地效果更好。

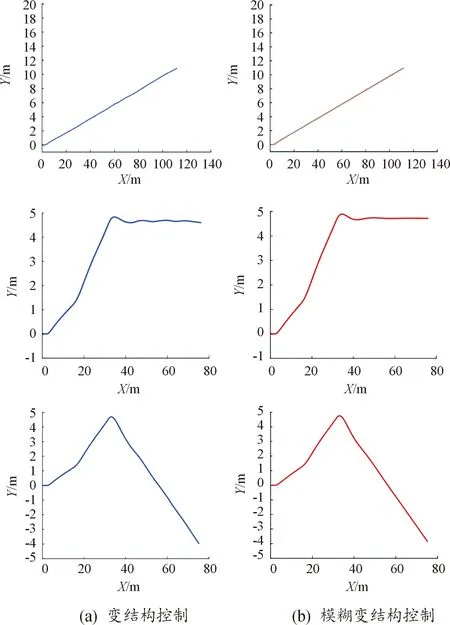
图8 2种策略控制下UUV侧向运动轨迹截图组Fig.8 Screenshot group of UUV lateral movement trajectory under the control of two strategies

3.3 抗扰性分析

将REMU S100作为演算案例,运用2种控制策略,通过仿真获得在模型参数(如各类水动力参数)变化情况下[13],UUV侧向运动轨迹变化情况,采用所谓标称参数系统(p)、上限参数系统(1.3 p)、下限参数系统(0.7 p)分别进行仿真计算。

仿真时假定系统的控制输入指令为正弦信号(此时图形更能呈现系统动态关系,更能清晰体现变结构控制对系统姿态控制效果),图9给出了在正弦控制输入下策略控制所对应的三类系统艏摇角响应。

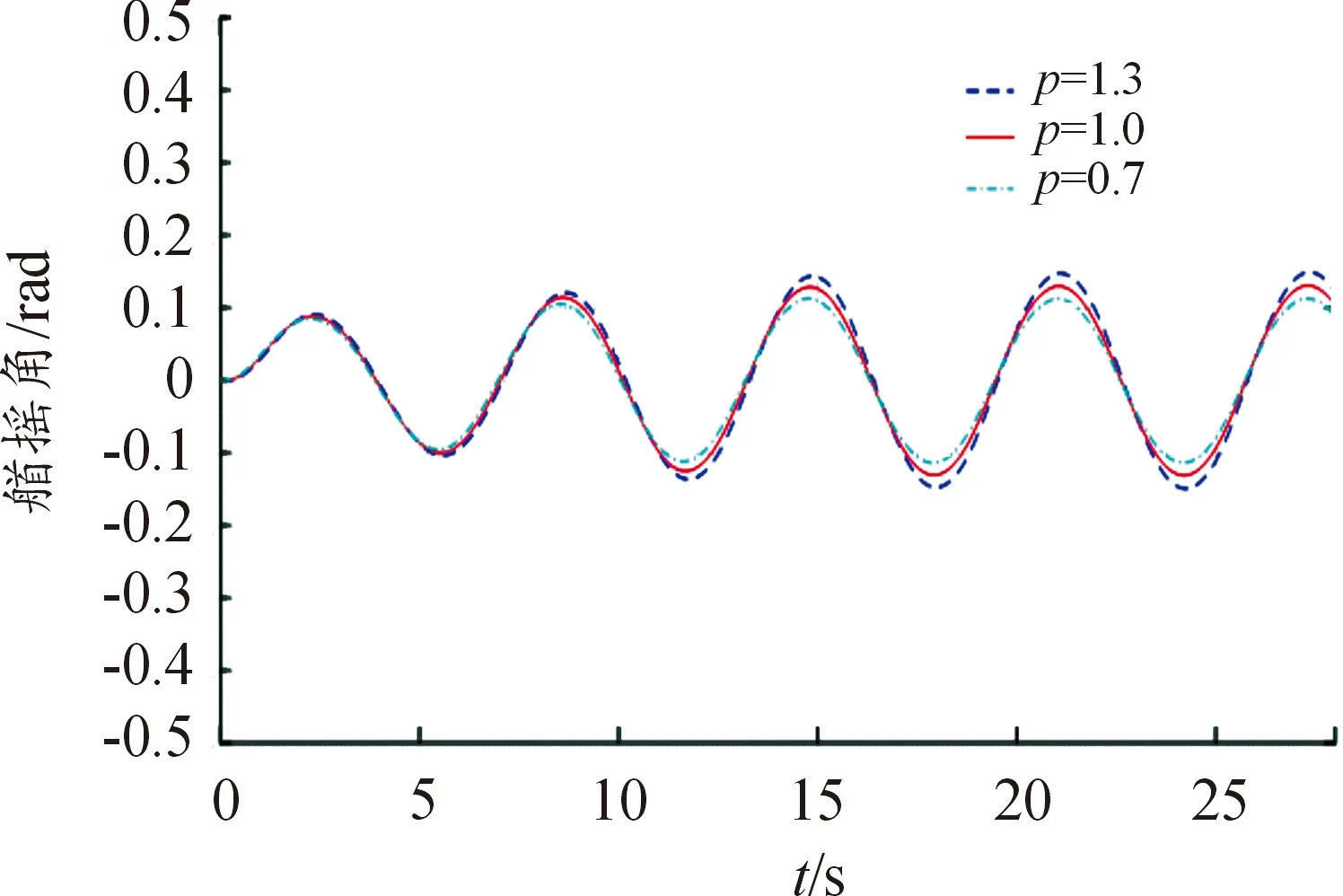
图9 正弦控制输入下三类系统艏摇角响应Fig.9 Bow angle responses of three types of systems under sinusoidal control input

通过观察图9中标称参数系统、上下限参数系统三类系统艏摇角响应曲线差异不难发现,即使模型参数发生较大变化(≦30%),变结构控制策略也显现出较强的鲁棒性,说明当模型参数受到外界扰动或在不同工况下差异较大时,2种控制策略控制也能够完成航向指令的准确跟踪。

3.4 噪声抑制分析

为了分析2种策略控制器在UUV航行控制中对于噪声的抑制情况,以侧向控制为例,在仿真分析时仍沿用前文中的原参数,然后在系统状态方程的控制输入中混杂一定量级的随机噪声,通过仿真来分析噪声对于运用策略控制在侧向航行运动中的影响程度,图10是混杂有扰动噪声的控制量输入,其中理想情况指仿真中加入了均值为0、方差为0.1的随机噪声,而低噪声情况和强噪声情况的随机噪声方差分别为1和10,图11—图14分别给出对应了变结构控制及模糊化控制下3个不同噪声级下切换面函数、横荡速度、艏摇角速度、艏摇角响应的仿真计算结果曲线。

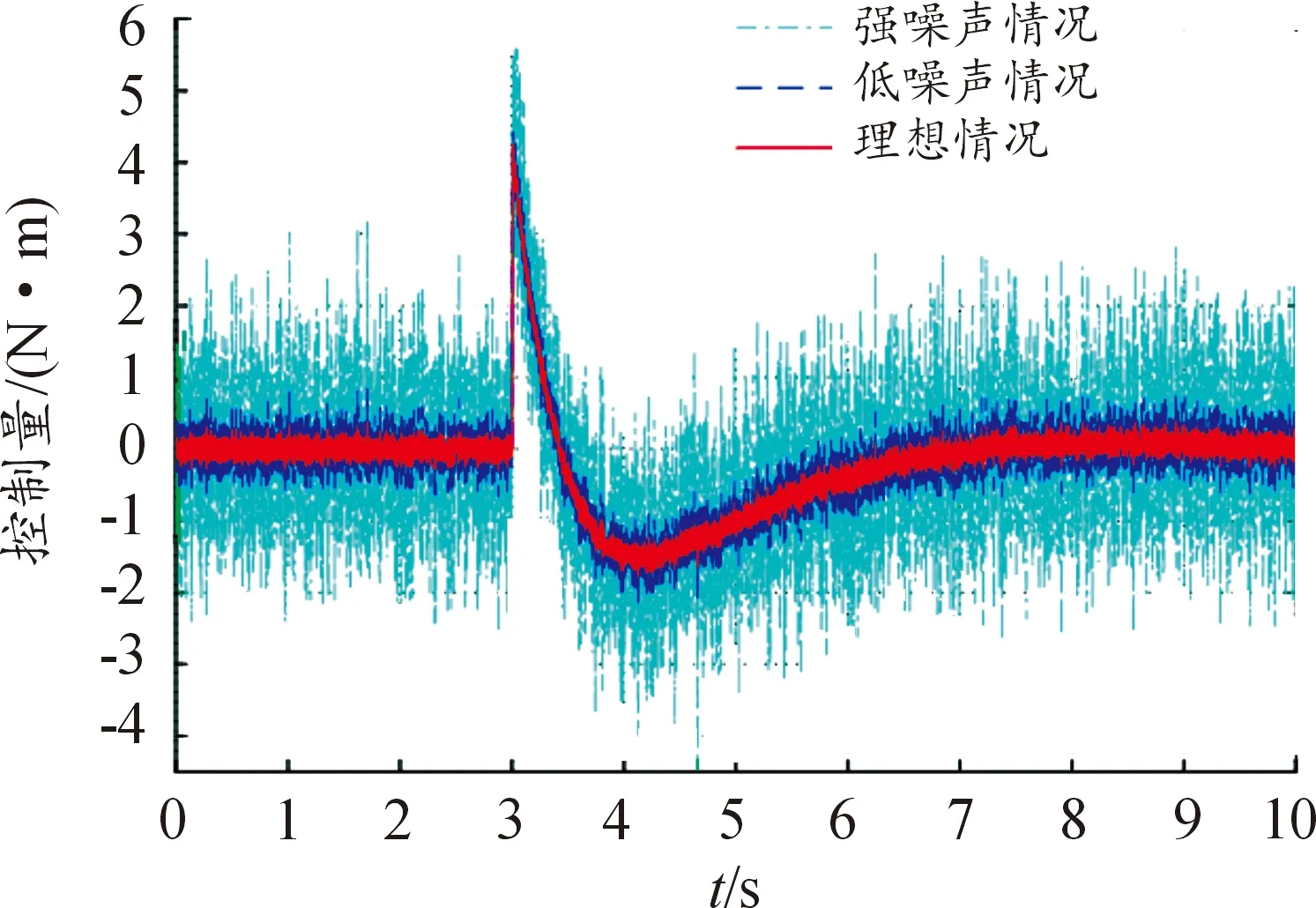
图10 混杂有扰动噪声的控制量输入Fig.10 Control input with mixed disturbance noise

图11 扰动噪声下的切换面函数响应Fig.11 Switching surface function response under perturbation noise

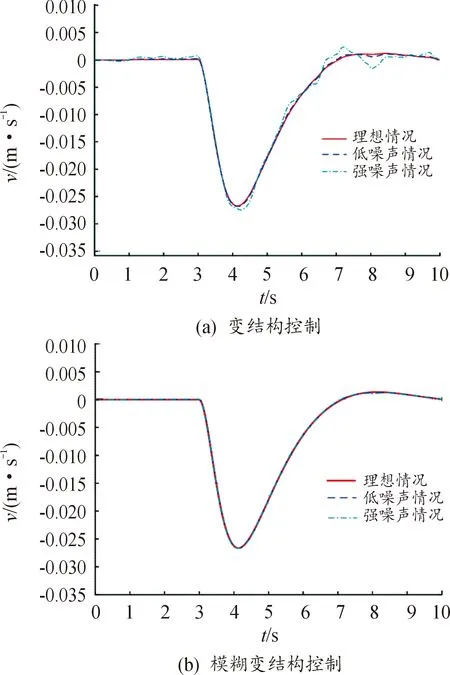
图12 扰动噪声下的横荡速度响应Fig.12 Swing velocity response under disturbance noise

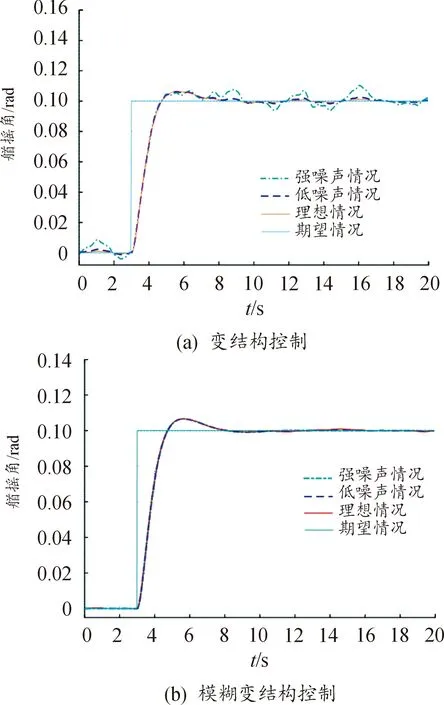
图14 扰动噪声下的艏摇角响应Fig.14 Bow angle response under disturbance noise

通过分析仿真结果,即便在较大噪声干扰下,变结构控制器及其模糊化控制器在UUV航向控制中的运用效果依旧比较稳定,能够满足实际控制需求。结果表明,变结构控制器及其模糊化控制器较好地抑制了干扰噪声,即采用这种变结构控制策略及其模糊化控制策略均可忽略噪声的影响。2种控制策略的响应曲线整体上相似,而其模糊规则应用的控制响应曲线相对更加地平滑,表现出更好的控制效果。在强噪声干扰下,发现变结构控制及其模糊化控制对于噪声的抑制效果慢慢变差,也就是说,变结构控制及其模糊化控制对于强干扰随机噪声的抑制并不是毫无尺度约束的,即所能抑制的随机噪声强度是有量级限制的,这个结论应该是客观的。

4 结论

本文在变结构控制策略的设计基础上,应用特定模糊规则,把控制策略中不连续的信号切换置换成连续的模糊逻辑信号切换,即运用模糊推理来柔化控制信号以自调整其控制参数,从而有效抑制了变结构控制中的抖振现象;同时验证了模糊化变结构控制策略不失为一种较好的非线性跟踪控制方案,其航向跟踪稳定、动态响应特性较好,同时具有良好的抗扰性能。