基于主从博弈的多柔性负荷两阶段优化调度

陈 鑫,林永君,白青飞,李 静

(华北电力大学,河北 保定 071000)

1 引言

近年来,电动汽车因其清洁高效的特点得到快速发展,但大量电动汽车(EV)随机接入电网进行无序充电,会给配电网的安全稳定运行带来显著影响[1,2]。因EV具有响应速度快控制灵活等特点,通过对其充放电的合理控制,不仅解决了上述问题,同时可为电网运行提供重要安全保障;但EV参与需求响应受车主意愿和响应时间限制具有较大的不确定性;空调因其虚拟储能特性现已成为最具潜力的需求侧资源之一[3]通过结合多类柔性负荷共同参与电网需求响应可解决一类柔性负荷在响应上的不确定性,提高其辅助服务质量。园区作为需求响应的主战场,包含大量柔性负荷,制定行之有效的园区运营商与柔性负荷用户间的互动策略引导其参与需求响应显得尤为重要。

目前,国内外针对柔性负荷参与电网响应的互动策略已开展了诸多研究,文献[4]针对大规模电动汽车无序充电带来的影响,基于分时电价制度和电动汽车可入网的情况,建立了计及电网负荷波动及用户成本的多目标优化模型,并通过与固定电价的对比验证了策略的有效性。文献[5]为解决光伏功率的随机波动对电网电能指令的影响,提出了微网环境下的集群电动汽车参与平抑光伏波动的控制框架,并建立了电动汽车跟踪光伏出力的凸优化模型。文献[6]利用V2G技术平滑大规模风电波动,通过引入背包问题建立电动汽车能量管理模型,并利用动态规划的方法提出了电动汽车和风电的优化调度策略。文献[7]针对不同类型的空调可调控潜力不同的特点,提出一种考虑不同空调负荷特性的多尺度微网优化调度策略,日前以最小化运行成本,日内以平滑联络线功率。文献[8]针对风电渗透率和负荷需求增加导致峰谷差增大的问题,提出一种分层控制策略,以协调多个机组的集中空调(AC)负荷及进行功率调节,以减少峰谷差。但上述文献并未考虑柔性负荷用户参与需求响应的意愿,可能会造成参与需求响应后用电费用不降反升。

为有协调各方利益,以实现多方共赢,文献[9]考虑多能源工业园区内热电联产机组所有者与工业用户间双向电和单项热交易的博弈互动过程,在两方共赢的基础上,实现调峰。文献[10]为实现代理商与电动汽车车主间的双赢,提出一种智能小区代理商的定价及购电策略。针对社区综合能源系统分布式特征,文献[11]提出一种基于主从博弈的社区综合能源系统分布式协同优化运行策略,将上层能源销售商作为领导者,新能源、负荷等聚合商作为追随者,求解各方的最优交互策略。为兼顾园区内不同主体间的利益,文献[12,13]考虑园区综合能源运营商间的供需双侧博弈互动,以兼顾供需两侧的利益最优。文献[14]结合激励手段和价格信号为售电商设计提供多类市场竞争力的零售套餐,并基于多时间尺度,构建了主方购售电组合决策模型和从方零售套餐选择模型。文献[15]为解决电动汽车用户通过电价响应峰谷倒置现象的发生以及多次充电的电池损耗与使用不便的问题,在上层考虑电网收益,在下层考虑电池损耗的主从博弈模型,但所设计模型在上层并未有可优化变量,仅为单层博弈问题。为解决电动汽车和空调的规模化接入使得配电网尖峰负荷持续增大的问题,文献[16]建立考虑电网公司与电动汽车代理商、储能运营商的主从博弈模型,上层构建运营收益最大与峰谷差最小的多目标函数,下层以用户收益最大为目标。文献[17]为解决需求与可再生能源发电间不匹配的问题,聚合商通过向用户提供奖金激励用户调整其负荷,实现用户与可再生能源预测间的匹配问题,通过考虑聚合商和用户间的互动过程,实现双方间的最佳响应。文献[18]研究社区综合能源系统中用户综合需求响应,建立用户优化用能模型和社区综合能源运营商优化模型,并分析了多能互补的用户综合需求响应行为,有效提升了能源利用率。

但上述有关主从博弈的文献均为日前调度计划,并未考虑日内预测偏差;同时在柔性负荷建模上忽略了其异构性的特点,针对上述问题,本文提出一种基于主从博弈的两阶段调峰优化框架,日前阶段建立以园区运行商削峰填谷并兼顾自身利益的上层优化模型,下层建立以柔性负荷用电费用最小优化模型,并基于主从博弈求得日前调度计划;日内考虑预测偏差,基于模型预测控制对柔性负荷进行合理调度以跟踪日前削峰填谷调度计划,使系统的鲁棒性得以提升。

2 两阶段优化调度框架

本文的整体框架见下图1。在日前建立运营商与用户间的双层博弈模型,在上层园区运营商通过制定电价策略引导柔性负荷参与削峰填谷同时兼顾自身利益,下层柔性负荷通过改变其用电行为减少用电成本;双边反复博弈以求得纳什均衡解;在柔性负荷建模上充分考虑空调的异构性以及电动汽车出行规律随机性等特点,利用蒙特卡罗模拟抽样得到空调异构参数以及电动汽车出行规律参数,在日内阶段,考虑光伏、风机出力的不确定性,基于模型预测控制以15min为间隔、4h为周期进行滚动优化调度,通过调整聚合柔性负荷出力以及储能系统充放电功率以跟踪日前电网联络线功率。

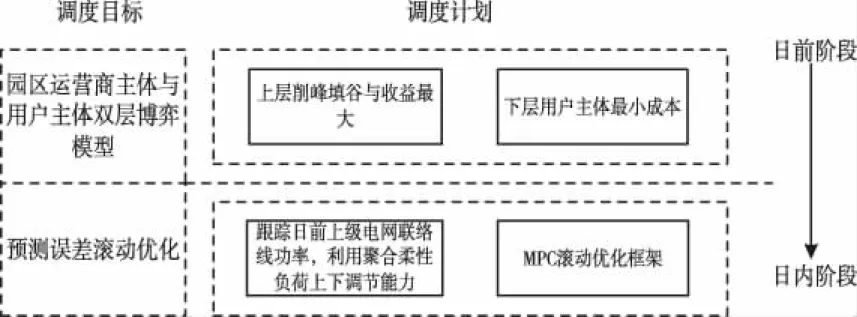
图1 两阶段调峰优化调度研究框架

3 日前博弈模型

在日前阶段考虑园区运营商与用户主体间的博弈关系,基于文献[14]-[16]建立如下双层博弈模型,上层园区运营商通过制定相应的电价政策以实现削峰填谷与自身收益最大,在上层所制定的电价策略的基础上,下层通过改变柔性负荷的用电行为,以实现自身运行用电费用最小,并将所求得的用电行为曲线返回至上层模型,上层模型在重新制定相应的电价策略,如此反复,直至求得最终的博弈均衡解双层博弈结构图如图2所示。

图2 日前双层博弈模型结构

图3 博弈模型求解流程

图4 日前预测数据

3.1 上层园区运营商模型

3.1.1 上层目标函数

上层运营商作为枢纽连接上级电网与下层柔性负荷用户,运营商结合自身可在生能源出力、电网交互电价、刚性负荷以及下层柔性负荷用电行为制定相应柔性负荷用电价格以实现削峰填谷并兼顾自身收益,上层目标如下所示

minf=ω1f1-ω2f2

(1)

式中:f1为削峰填谷目标函数,f2为运行商收益目标函数,ω1、ω2分别为各目标归一化的权重值。

采用负荷均方差最小作为削峰填谷的优化目标,可表示为

(2)

(3)

式中:Pload,sum(t)为t时刻总负荷值,Pload(t)为t时刻刚性负荷值,PEV1,i(t)、PEV2,i(t)为t时刻住宅区、商业区电动汽车充电功率,Pair,i(t)为t时刻空调功率,N1、N2、N3分别为住宅区、商业区电动汽车数目以及空调数目。

为引导柔性负荷参与需求响应的同时应保证园区运营商自身利益,成本目标可表示为

f2=C1+C2+C3

(4)

式中,C1为与上级电网交互成本,C2为柔性负荷用电费用,C3刚性负荷用电费用。

(5)

(6)

(7)

式中:Pload(t)为与上级电网交互功率,CGrid+(t)、CGrid-(t)为与上级电网交互电价,Cbuy(t)为柔性负荷用电费用。

3.1.2 功率平衡条件

(8)

式中:PPV(t)、PWV(t)为光伏、风机t时出力。

3.1.3 储能设备约束

通过在系统中增设储能设备可在日前发挥削峰填谷的作用,同时其快速性的特点使得其在日内阶段可较好的跟踪日前调度计划,所建立储能模型如下所示

SOC(t)=SOC(t-1)+

(9)

(10)

SOCmin≤SOC(t)≤SOCmax

(11)

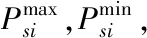
3.2 下层柔性负荷模型

3.2.1 下层目标函数

下层柔性负荷包含聚合电动汽车负荷与聚合空调负荷,基于上层运营商制定的各时段电价,下层用户通过改变自身的用电行为以实现用电成本最小,所建立下层成本目标可见下式

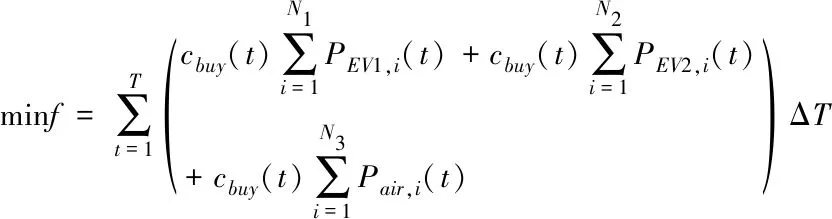
(12)

3.2.2 电动汽车聚合模型

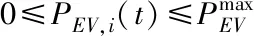
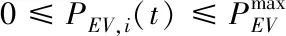
(13)

SOCEV,i(t)=SOCEV,i(t-1)+ηevPEV,i(t)

(14)

SOCEVmin≤SOCEV(t)≤SOCEVmax

(15)

(16)

受充电桩个数,同时为保证电动汽车可更好的发挥削峰填谷能力,设置各时段聚合充电功率上限

(17)

3.2.3 电动汽车出行规律模型

基于蒙特卡罗对园区内,商业区、居民区的电动汽车出行分布函数进行随机抽样,以模拟电动汽车随机出行规律;其分布函数见下式

(18)

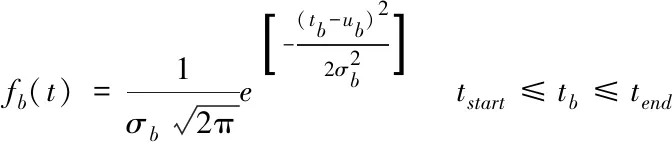
(19)

其中,式(18)为住宅区返回时刻分布函数,式(19)为商业区到达时刻分布函数;th为住宅区用户返程时间,μt为期望值取17.6,σt标准差取3.4;tb为商业区用户返程时间,μb为期望值取11,σb为标准差取3,tstart、tend为起始结束时间取4、20。

3.2.4 空调聚合模型

由于单一空调可调度能力较小,故对其进行聚合;在空调聚合时考虑空调的异构性,针对第0≤Pi,VESS(t)≤Pi,VESS,max台空调所建立如下约束

0≤Pi,VESS(t)≤Pi,VESS,max

(20)

CVESS,i(t)=COPVESS,iPVESS,i(t)

(21)

(22)

Tmin≤TVESS,i(t)≤Tmax

(23)

其中,式(20)为空调的出力功率上下限约束,Pi,VESS,max为空调出力上限,式(21)为空调制冷/热量等式,COPVESS,i为空调制冷/热能效比,式(22)为改进一阶ETP模型;式中ρ、C分别为室内空气的密度、热容,Vi、CVESS,i为第i住户的住宅体积、空调制冷/热量,Awini、Awalli、kwini、kwalli分别为住户i的外窗、外墙面积,以及外窗、外墙传热系数,N为与i住宅相邻的住宅数目,Anextj、knextj为相邻内墙面积、传热系数,Ti(t)、Tout(t)、Tj(t)分别为t时刻i住宅温度、室外温度、相邻j住宅室内温度,式(23)为空调虚拟储能调节带宽,Tmax、Tmin为所设置温度上下限。

4 日前博弈模型求解方法

由于粒子群算法收敛速度快,且具有一定的记忆性,可以很好的模拟园区运营商与用户间电价的博弈互动过程,同时个体与群体的协同优化有助于快速寻找博弈均衡解;所建立模型中具有大量等式约束条件且在用户层面充分考虑电动汽车随机性与空调异构性的特点,属于大规模复杂优化问题,利用YALMIP工具箱中的CPLEX求解器可以有效解决大规模复杂问题,同时可以有效解决PSO启发式搜索算法随机性的缺点,故参考文献[14]采用一种结合粒子群与CPLEX的求解方法,博弈模型求解流程图如下所示;

1)设置粒子群数量与迭代次数;

2)初始化粒子群算法参数,生成电价信息初始粒子;

3)下层用户根据电价利用CPLEX求解得最优用电行为曲线;

4)上层园区运营商依据上层用户用电行为曲线合理调控储能系统以实现其自身收益最大;

5)以上层园区运营商收益最大作为粒子适应度函数目标值,基于所设置参数更新粒子的速度和位置;

6)判断是否达迭代次数,比较与前一轮迭代的最优结果值|Xn-Xn-1|≤σ,其差值若小于精度则求得博弈均衡解;

7)若不满足则重复上述2)-5);

5 日内优化模型

5.1 日内预测模型

日内考虑风、光以及负荷日前预测的不确定性,利用模型预测控制(Model Predictive Control, MPC)修正日内实际运行计划与日前调度计划间的偏差[19]。选取电网联络线功率、光伏功率、风机功率、负荷功率、储能系统充放电功率、空调聚合功率、电动汽车聚合功率等8个决策变量所构成的向量组作为状态变量,所建立状态变量为x(k)=[Pgird(k),Ppv(k),Pwt(k),Pload(k),Psi(k),Pair,sum(k),PEV,sum(k)]T,以储能系统和聚合空调出力增量构成的向量作为控制变量u(k)=[ΔPsi(k),ΔPsum,air(k),ΔPEV,sum(k)]T,以光伏,风机,以及负荷超短期预测作为扰动输入r(k)=[ΔPpv(k),ΔPwt(k),ΔPload(k)]T,可建立式(24)预测模型,并反复迭代向前预测Np时段

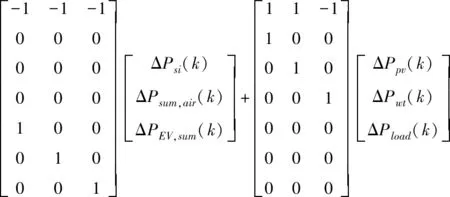
(24)

5.2 日内目标函数

日内滚动优化的目标为修正日内实际运行值与日前调度值的偏差,同时使储能发挥日前削峰调谷作用;目标函数如下式(25)所示

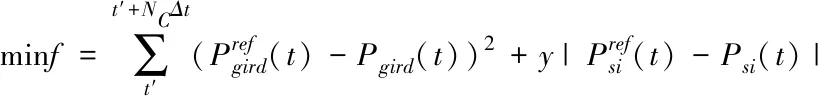
(25)

5.3 约束条件

5.3.1 功率平衡条件

PPV(t)+PWT(t)+Pgird(t)=

Pload(t)+Psi(t)+Psum,air(t)+PEV,sum(t)

(26)

式中:PPV(t)、PWT(t)、Pload(t)分别为日内光伏、风机负荷预测出力,Psum,air为空调聚合功率。

5.3.2 聚合柔性负荷约束

(27)

5.3.3 聚合柔性负荷约束

储能系统约束见式(9)-(11)。

6 算例分析

本文基于某典型园区开展相关算例验证,该园区包含光伏发电系统其装机容量为1800kW,风力发电系统装机容量为2500kW,储能系统额定容量为750kVA,电动汽车,空调等多柔性负荷以及刚性负荷。该区域配有200台分体空调有意向参与聚合调度其面积服从均值为100m2的正态分布、房屋材料等参数均服从正态分布,分体式空调出力上限服从2kW正态分布,空调屋外温度选取某冬季典型日温度曲线,室内温度结合热舒适性将温度带宽设为21℃-25℃;电动汽车基于典型住宅区、商业区出行规律曲线利用蒙特卡罗模拟该园区各区域200辆电动汽车随机出行规律,各设备参数可见下表1,基于所提出的两阶段优化框架,可做如下算例验证。

6.1 日前优化调度

日前优化阶段,以24h为调度周期,调度时间间隔取1h,图5为日前小时级、光伏、风机与负荷预测曲线,基于刚性负荷需求侧响应设置运营商与上级电网间交互电价如图虚线所示上曲线为购电价格下曲线为售电价格;

图5 迭代收敛结果

基于结合粒子群的CPLEX求解方法对所建立的园区运营商与柔性负荷用户主体间的双层博弈模型进行求解;

通过图5可知,通过两方的博弈,上下层函数均呈收敛趋势,即园区运营商层引导柔性负荷参与需求响应逐步提高,同时自身收益增大使上层目标函数逐渐降低;下层柔性负荷用电成本呈下降趋势,在迭代达45次左右上下层函数趋于稳定,说明求得博弈均衡解,从而证明了所建立博弈模型的有效性;仿真结果如下;

博弈电价见图6所示,其中上虚线为所设置电价上限,下虚线为所设置电价下限,实线为博弈电价,对比图8中响应前负荷即圆形标注曲线可发现,博弈电价在负荷谷值时取电价下限,如图中1:00-7:00,在负荷峰值取较高电价;见18:00-20:00时刻,为保证园区收益,在该时段电价出现波动以增加园区收益;图7为聚合柔性负荷响应曲线不难看出博弈电价曲线趋势与柔性负荷用电行为呈对应关系,在9:00、18:00-20:00等时段为电价峰值时段,此时聚合电动汽车聚合功率为零或维持在较小值、聚合空调负荷作为虚拟储能参与“放电”,在电价谷时段见1:00-7:00、11:00-13:00此时空调进行制热为虚拟储能充电,由于空调作为虚拟储能设备其储能连续充放电维持时间较短,为减少其用电成本故空调功率在1:00-3:00缓慢增加,电动汽车在此时段进行充电,将聚合功率维持在较高值,图中7:00为电动汽车聚合功率峰值时刻此时一方面是由于电价较低,另一方面是由住宅区电动汽车为满足出行要求进行充电。图8为响应前后削峰填谷曲线;其响应前曲线为刚性负荷加各异构空调维持在23度时的功率加电动汽车按调度时段平均充电功率所得;对比曲线可明显看出,执行该策略后负荷峰谷差由原来1613kW降至906.3kW,所提出的博弈策略在日前阶段可有效引导柔性负荷参与需求响应,同时达到平滑电网联络线的目的。文中在建立柔性负荷模型充分考虑空调的异构性与电动汽车的随机性的特点,其典型空调与电动汽车数据可见下表所示。

图6 上层博弈电价曲线

图7 下层聚合柔性负荷曲线

图8 削峰填谷对比曲线

图9 聚合电动汽车场景对比曲线

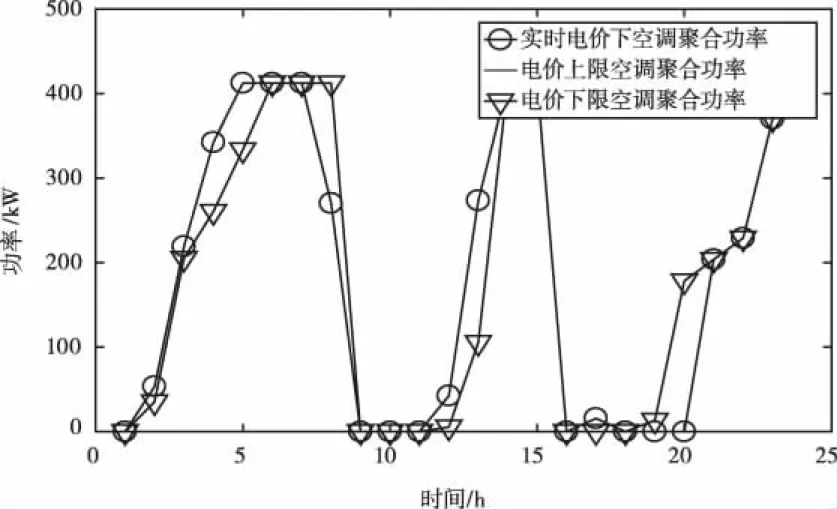
图10 聚合电空调场景对比曲线

图11 可再生能源预测对比曲线

通过上表可知,表2、3分别为住宅与商业区典型电动汽车充电曲线,其阴影部分表示其可调度时段,不难看出各电动汽车的充电规律类似,基本与电价曲线呈反比关系;表4为异构空调数据,可以看出空调受异构性的影响其最大功率不同,各单体空调运行曲线均与电价曲线成反比,从而验证了所提博弈策略引导柔性负荷参与需求响应的有效性。上层目标在设置时在引导柔性负荷参与需求响应的同时以提高园区运营商收益,为此对比不同电价策略下,园区运营商的收益,其不同电价策略下柔性负荷成本与园区运营商收益可见下表。

表2 典型住宅区电动汽车充放电数据

表3 典型商业区电动汽车充放电数据

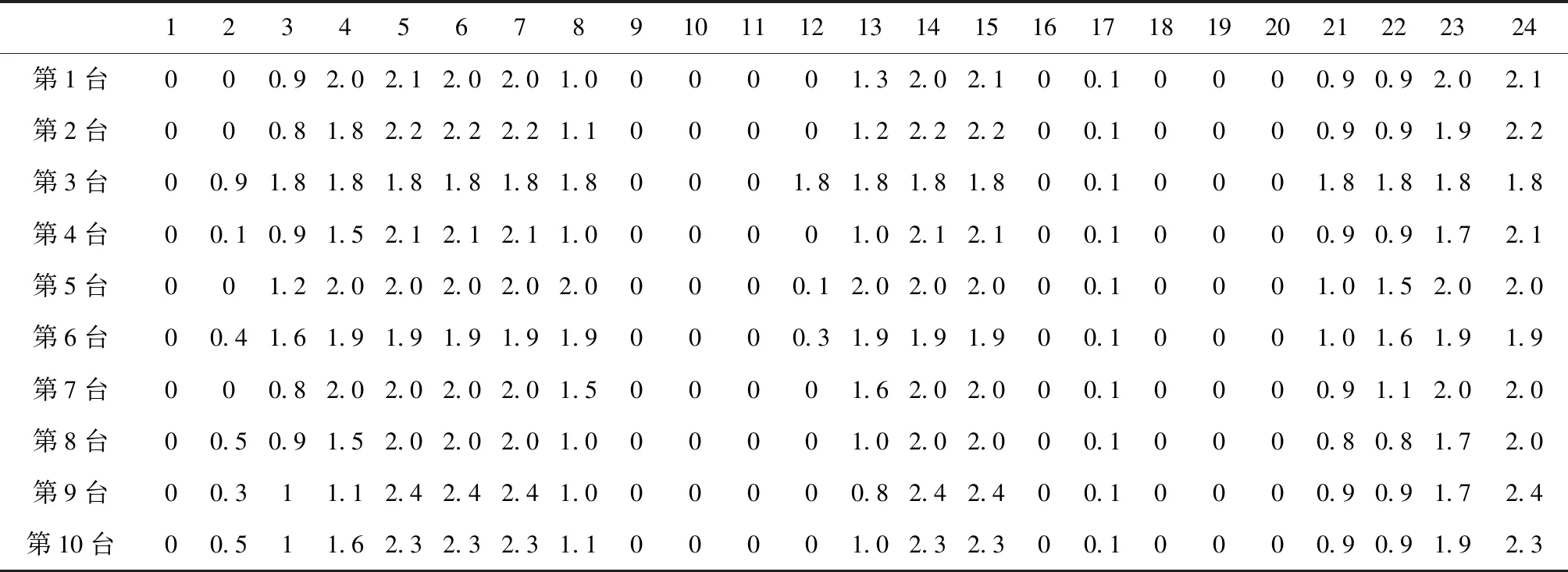
表4 典型空调数据

表5为对比电价参与博弈与不参与博弈的三种情况,当电价取下限时见场景1,此时运营商主体由电价较低此时收益最低为31736.2元,柔性负荷主体由于电价较低其用电成本最低5137.9元;当电价取上限见场景2,此时运营商主体由电价设置较高收益最高为34809.4元,柔性负荷主体则因电价较高使得用电成本最达7856.8元;通过结果可知场景1、场景2、均未兼顾运营商主体与柔性负荷主体双方的利益,一方利益最佳必定会牺牲另一方的利益,对比场景3电价参与博弈,柔性负荷主体依据博弈电价改变自身的用电行为,此时运营商收益为32568.5元,柔性负荷主体收益为5439.8元,对比场景1、2可知所得结果为两方获益的折中方案,可见所设计双层博弈模型在引导柔性负荷有效参与需求响应的同时可兼顾运营商主体与柔性负荷主体间的利益。不同场景下的聚合柔性负荷用电行为可见下图所示。

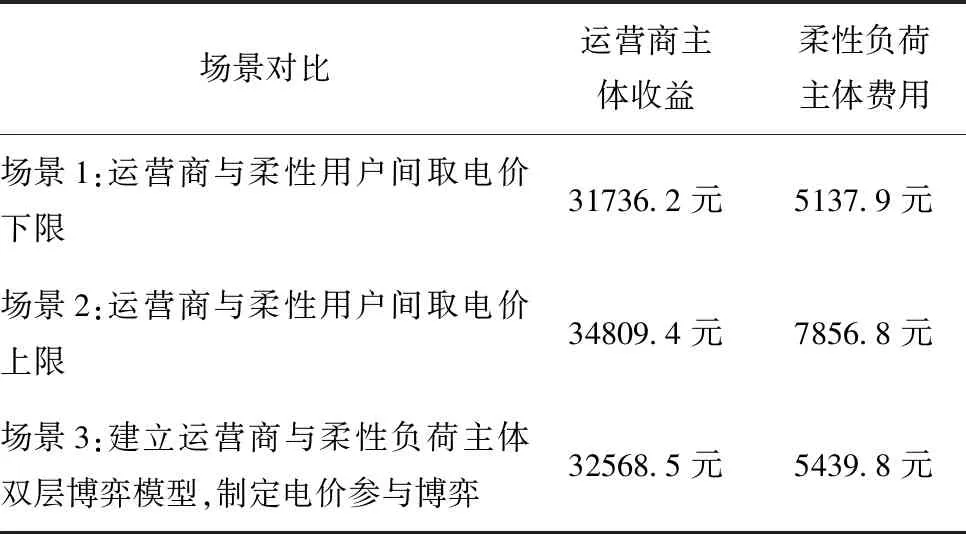
表5 不同场景下双侧主体价格对比

上图为不同场景下电动聚合电动汽车充电功率曲线,不难发现曲线大体趋势相同,因电动汽汽车设置时段最大充电上限,故场景1和场景2曲线会稍有差别,但都满足在电价较低时进行充电以减少用电费用;

上图为不同场景下聚合空调对比曲线,因场景1与场景3电价趋势相同故聚合曲线重合,其在电价较高时“放电”电价较低时“充电”。

6.2 日内优化调度

在日内阶段考虑风预测的不准确性,采用MPC方法修正日内实际运行计划与日前调度计划间的偏差。通过对聚合柔性负荷以及储能出力的调整以跟踪日前调峰计划。日内场景集由日前功率预测曲线叠加随机误差模拟得到[19],日前日内可再生能源预测对比曲线见下图;

基于式(24)-(27)所建立的日内优化模型进行滚动求解,所求得联络线对比曲线见图12。

图12 日前日内联络线对比曲线图

不难发现通过对聚合柔性负荷与储能的日内调整可以使联络线紧密跟踪日前计划值,从而实现二次调峰效果,验证了日内策略的有效性,通过对联络线的二次平滑可以避免因可再生能源预测偏差导致微网联络线功率的剧烈波动,影响电网的稳定性;

图13为聚合电动汽车负荷为应对可在生能源与刚性负荷的预测偏差日内调整曲线,可看出当可在生能源出力过大时,电动汽车与空调在其调整范围内进行充电以消纳富裕可再生能源,当可在生能源不足时,柔性负荷减少用电或放电以满足刚性负荷需求,聚合空调功率日前日内对比曲线与此类似。

图13 聚合电动汽车日前日内对比曲线

图14为储能系统日前、日内对比曲线,为跟踪日前电网联络线功率储能系统在日前基础上进行不断调整,因目标函数中增加储能项以满足其日前削峰填谷作用,不难发下其趋势大体可跟踪日前计划,但并不紧密,可考虑增大储能占比权重。

图14 储能系统日前日内对比曲线

7 结束语

为实现园区运营商与柔性负荷间的共赢,引导柔性负荷参与需求响应,本文提出了一种基于主从博弈的多柔性负荷两阶段调峰优化模型,在日前阶段基于所建立双层博弈模型,上层园区运营商通过制定电价以实现自身目标最大化,下层用户基于制定电价调整其用电行为以减小成本;并采用结合粒子群与CPLEX的求解方法对博弈模型进行求解以更好的模拟博弈过程,以高效的求得博弈均衡解,文中对比分析了响应前后负荷峰谷差值与不同电价情况下运营商与柔性负荷用户的目标值,验证了基于所设计博弈模型的有效性,在日内阶段基于所建立预测模型利用多类柔性负荷以及储能系统协调调度以跟踪日前电网联络线功率,从而实现对联络线的二次平滑,研究所得结论如下:

1)在日前建立双层博弈模型,上层园区运营商制定相应电价,下层用户依据所制定电价对柔性负荷的用电行为进行调整,经过多次博弈求得纳什均衡解,从而实现各方目标利益的最大化。

2)在多柔性负荷协调调度上,充分考虑空调的异构性参数以及电动汽车随机性特点,以求得更为精确的调度计划。

3)在求解方法上,利用结合粒子群与CPLEX的求解方法以更好模拟双方的博弈互动过程,同时可更高效求得博弈均衡解,对比响应向后负荷峰谷差,与不同电价策略下各主体利益验证了所设计博弈模型的有效性。

4)日内考虑预测的不准确性,通过日内对聚合柔性负荷的短时灵活调节,以跟踪日前联络线功率实现对联络线的二次平滑,提升了系统的鲁棒性。