基于地面约束的改进A-LOAM算法

王乐兵,王 挺,姜 祎,李亚伟

(1. 中国科学院沈阳自动化研究所机器人学国家重点实验室,辽宁 沈阳 110016;2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;3. 中国科学院大学,北京100049)

1 引言

随着机器人导航技术的发展,SLAM已成为近些年的研究热点,其精度和鲁棒性的提高也面临诸多挑战[1]。激光雷达是SLAM算法常用的传感器之一。激光传感器的测量信息不受光照等环境因素的影响且可以直接获得环境的深度信息。以激光雷达为传感器的激光SLAM算法应用前景广阔。

LOAM[2][3]是激光SLAM的代表算法,该算法首次提出了粗匹配到精匹配的优化框架,Odometry线程负责利用相邻两帧间的特征点实现粗匹配,实时跟踪位姿变化,Mapping线程则将特征点与局部地图匹配进一步优化位姿。A-LOAM是LOAM算法的简化版本。LeGO-LOAM[4]在LOAM的基础上对激光点云进行了更精细的处理并增加了回环检测。HDL-graph-slam[5]是基于点云配准的3D激光SLAM算法,除此之外该算法还假设了全局一致地面的存在用于约束机器人位姿。由于激光雷达获取的真实点云存在运动畸变、缺少特征等情况,导致基于匹配的SLAM算法在应用于地面机器人时随着时间增加会产生较大的高程误差,如何提取环境中的有效信息进行配准是激光SLAM算法的挑战。

本文针对地面机器人提出一种基于地面约束的改进A-LOAM算法。在数据预处理时通过分割地面点与非地面点提取更为可靠的特征用于匹配。Odometry阶段则负责构建增量式里程计,实施跟踪位姿变化。Mapping阶段将Odometry的结果作为初值,通过闭环检测、地面约束和局部地图结束进一步优化位姿。与HDL-graph-slam中的全局一致地面不同,本文通过在局部地图中提取地面约束机器人的位姿,当机器人所在环境地面发生变化时,该约束仍有效。

2 改进的A-LOAM算法框架

为了改进纯激光SLAM算法A-LOAM在应用于地面机器人时出现的特征匹配不可靠、高程误差漂移等问题,本文在该算法基础上构建了基于地面约束的激光SLAM算法,算法结构示意图如图1所示。与A-LOAM框架不同的是本文算法增加了回环检测阶段。

图1 改进的A-LOAM算法结构示意图

2.1 数据预处理

为了获取更精确的匹配结果,本文首先对原始激光点云做去畸变的处理,然后进行特征点的提取。

2.1.1 畸变去除

在机器人运动过程中,激光点云中的每个点都是在不同的基准位姿获取的,从而导致点云的运动畸变,尤其是当激光雷达扫描频率较低或机器人运动较快时,这种运动畸变不可忽略。去除点云运动畸变的基本思想是将一帧点云内的点转换到同一时刻的(一般是该帧的起始或结束时刻)基准位姿上。假设一帧时间内获取的点云为P,机器人在该段时间的位姿变化估计为ΔR和Δt,利用插值得到每个点相对于起始时刻的运动,进而每个点将换到该帧起始时刻去除运动畸变。

2.1.2 特征提取

特征提取即从点云中提取能够反映当前环境信息的特殊点,例如角点一般位于拐角,平面点则位于平面上。考虑到地平面也属于平面且地平面中的点对匹配精度影响不大,因此在提取特征点之前,首先标记点云中的地面点和非地面点。只在非地面点中选取角点和平面点以提高效率,地面点则用于后续的地面约束。

2.2 Odometry阶段

在odometry阶段,接受来自传感器的信息进行帧间匹配,获得增量式里程计。

对非地面点云计算每个点的局部平整度c,c值较大的作为角点,较小的作为平面点。

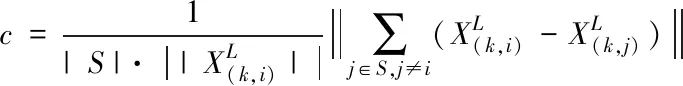
(1)

通过分割地面点和非地面点可以提取到更可靠的特征点信息从而降低匹配误差。

2.2.1 点云匹配

点云特征匹配的方法[6][7]有最近点迭代法(Iterative Closest Point,ICP)[8][9]、正态分布变换(Normal Distribution Transform, NDT)[10][11]和基于特征的匹配方法[2]。

基于特征的匹配与ICP匹配方法的区别在于源点云在目标点云中的匹配不再是一个点,而是一条直线或一个平面。该直线(平面)由源点云在目标点云的邻近点表示(如图2所示,i是源点云中的某一特征点,j、l、m为该点在目标点云中的匹配点)。将源点云某一点与其匹配点变换到同一坐标系后利用点到线和点到面的距离构建残差,通过迭代优化匹配残差即可得到源点云和目标点云间的相对位姿,将连续两帧间的相对位姿累积即可获得激光雷达相对于初始时刻的位姿。

图2 角点(左)与平面点(右)的匹配

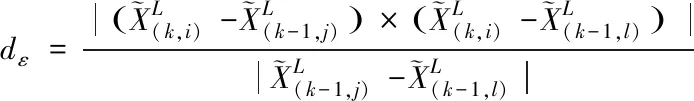
(2)

(3)

2.3 Mapping阶段

Odometry部分实现了帧间匹配,实时跟踪两帧点云间的位姿变化。由于匹配时仅将当前时刻的位姿与上一关联,累积误差将随着时间增加而增大。实际中机器人某一时刻位姿与之前多个时刻均存在“共视关系”,将这些时刻作为关键帧并利用关键帧点云构建局部地图进一步优化位姿,提高轨迹估计精度。

2.3.1 关键帧提取

Mapping阶段位姿优化时局部地图来自当前时刻机器人所处位置的附近关键帧点云,关键帧的数量和质量决定当前帧与局部地图的关联强度。除此之外回环检测也是基于关键帧进行的。若关键帧选取不合理可能会遗漏真闭环或者出现过多相似的闭环候选帧。因此关键帧的选取对提高算法的效率和精度至关重要。因此本文以两帧间的点云关联性和机器人的相对位姿为条件选取关键帧,尽可能使其均匀分布在机器人行驶路线上。

2.3.2 局部地图匹配

仅依靠相邻两帧的点云信息的位姿估计结果可靠性不高且会导致误差传递和累积。Mapping阶段利用帧间匹配的结果作为初值,将当前点云与局部地图对齐进一步优化位姿。除此之外,还利用局部地图中的地面信息进一步约束位姿估计在Z轴方向的误差(包括Z轴位移、俯仰角和横滚角)。在将当前帧点云注册到局部地图的同时,检测当前帧是否与历史帧形成闭环进一步约束关键帧位姿估计结果。全局位姿优化框架如图3所示。

图3 位姿约束示意图

2.3.3 地面约束

本文提出的算法主要针对地面机器人,由于机器人的Z轴位移不会突变,因此考虑加入地面约束。由于实际环境中不存在绝对平坦的地面且可能出现斜坡、楼梯等情况,因此本文用于约束机器人位姿的地面不是全局一致地面,而是跟随局部地图变化。在1.1.2小节提取特征点时已经对地面点和非地面地进行标记。将局部地图和当前点云中的地面点分别拟合为一个地面(如图4(a)所示),记为π0和π1。

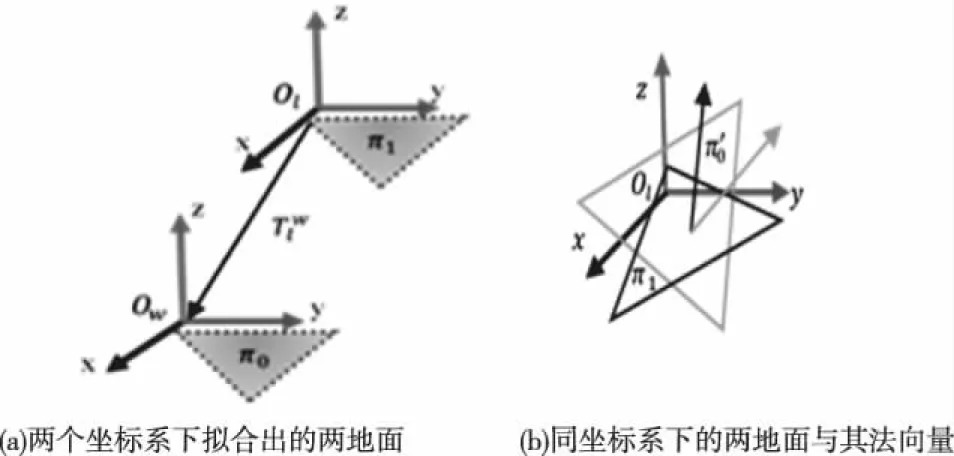
图4 地面约束原理

假设局部地图地面某点pm=[xm,ym,zm]T,法向量nm=[xnm,ynm,znm]T,则π0在全局坐标系中的参数方程为

(x-pm)·nm=0

(4)

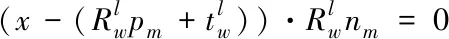
(5)

也可化简为如下形式

A0x+B0y+C0z+D0=0

(6)

同时π1在激光雷达坐标系中的参数方程表示为

A1x+B1y+C1z+D1=0

(7)

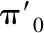
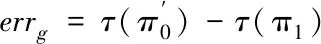
(8)

Mapping阶段接收到新的一帧点云后,利用该帧点云和局部地图中的地面点拟合出两个平面并根据平面参数构建残差参与位姿优化,对位姿进行修正。

2.2 回环检测

Odometry阶段和Mapping阶段构成一个开环的地面机器人SLAM系统,随着运行时间变长,累积误差也不断增加。回环检测是减小累积漂移误差的重要步骤[9]。本文将历史位姿以关键帧的形式存储,通过搜索当前帧附近的历史关键帧进行闭环检测,将距离最近的历史帧标记为闭环候选帧并利用ICP算法将当前帧与其匹配。如果匹配结果收敛,说明当前帧与候选帧相似度很高,符合闭环条件。最后将ICP算法得到的两帧间的相对位姿作为约束对与当前帧关联的关键帧进行位姿调整,减小累积误差。

3 实验

以下实验均在Ubuntu16.04环境下完成,计算机型号为NUC8I7HVK。本文所用实验数据来自两个公开数据集:KITTI[13]和GroundRobotDatabases[14](以下分别以Part＿s00和R4＿01表示)。其中GroundRobotDatabases是由中国科学院沈阳自动化研究所发布的面向地面移动机器人的数据集,内含16线激光雷达、双目相机、IMU、编码器等传感器数据,覆盖室内长走廊、室外开阔草坪、斜坡、楼梯以及地下车库等各种复杂环境。

参与实验的算法有A-LOAM、OUR及OUR＿NGC。其中OUR为本文提出的包括所有约束的完整算法,OUR＿NGC表示去除地面约束后的本文算法。

3.1 算法精度对比

为了验证提出的改进版A-LOAM算法的性能,本文估计了上述两个数据集的轨迹,如图5和图6所示((a)为本文提出的算法轨迹估计结果,(b)为A-LOAM轨迹估计结果)。图中虚线为groundtruth。

图5 轨迹估计结果(Part＿s00)

图6 轨迹估计结果(R4＿01)

为了定量评估算法的精度,本文还对比了A-LOAM和本文提出的算法(OUR)在上述两个数据集的估计轨迹与真实轨迹间的误差(均方根误差RMSE、标准偏差STD、误差均值MEAN和最大误差MAX),结果如表1、表2所示。

表1 两种算法的轨迹估计误差(Part＿s00)

表2 两种算法的轨迹估计误差(R4＿01)

本文在R4＿01上验证了回环检测的效果。根据图7中轨迹估计误差随时间的变化曲线((a)为本文算法,(b)为A-LOAM)。可以看出与(b)相比,(a)的误差增长趋势得到有效抑制。

图7 轨迹误差变化曲线(R4＿01)

3.2 地面约束可靠验证

除此之外,为了验证本文提出的地面约束对提高算法精度起到了积极作用,测试有地面约束(OUR)和无地面约束时(OUR＿NGC)的两种算法在数据集Part＿s00的轨迹估计结果,如图8所示,其中虚线为groundtruth,蓝色为带有地面约束的算法结果,绿色为不带地面约束的算法结果。由该图可以看出,加入地面约束后的轨迹估计更加靠近groundtruth。

图8 两种算法轨迹估计结果(Part＿s00)

由表3中的各种误差值也可看出,加入地面约束后除最大误差的其它误差均有下降,这说明加入的地面约束可以作为有效信息约束轨迹估计的误差。

表3 两种算法的轨迹估计误差(Part＿s00)

4 结束语

针对现有纯激光SLAM算法应用于地面机器人存在高程误差漂移的问题,本文提出了一种基于地面约束的改进A-LOAM算法。算法接收到激光点云后首先进行畸变去除并优化特征点提取过程获得更为可靠的特征,然后在Odometry阶段匹配特征实时跟踪位姿变化,在Mapping阶段本文算法采用了关键帧策略节省存储空间,根据关键帧构建局部地图并加入地面约束和回环检测进一步约束机器人位姿,减小累积误差,最终实现精确估计机器人的位姿。

本文在两个公开数据集上设计了实验用于验证算法性能。通过本文算法和A-LOAM的估计轨迹与groundtruth对比结果可得,本文提出的算法轨迹估计结果精度更高,且加入的地面约束可以有效降低误差。