通信网络用户涉密信息安全动态预警仿真
王梦晓,刘学军,操凤萍
(1. 东南大学成贤学院,江苏 南京 210088;2. 南京航空航天大学计算机学院,江苏 南京 211106)
1 引言
信息全面化具有巨大网络通信便利的同时,也存在信息贩卖、数据丢失、隐私泄露等弊端,在通信网络的建设中,提高信息传输的可靠性和安全性是研究领域的研究重点,因此通信的安全问题成为目前亟需解决的热点问题[1,2]。
针对通信网络涉密信息的安全问题,魏墨济[3]等人抽取先验知识作为模型顶层,并通过扩展顶层本体构建模型构架,然后定向采集通信网络涉密信息的社会立场库集合,并根据应用实例推算出相关主题的社会立场,最后将社会立场输入到模型中得到预警相悖度,完成通信网络涉密信息安全预警。该方法没有利用样本估计理论确定异常状态下的网络涉密信息,导致预警的准确率较低。焦萍萍[4]等人利用大数据采集技术中的采集函数获取通信网络的涉密信息数据,然后构建网络安全预警神经网络模型,最后将涉密信息输入到模型中学习训练,完成通信网络信息安全的预警。该方法没有利用样本估计理论找出异常状态下的网络涉密信息,导致预警结果的准确率较低,并且预警误报率较高。黄志胜[5]等人利用层次分析法计算出通信网络涉密信息的各级权重指标,然后使用隶属度函数算法对各级权重指标做归一化处理,并建立基于层次分析与区间预测的风险度评估等级标准,最后在此基础上构建反向传播的神经网络模型,通过多目标加权函数计算出动态预警范围,完成大规模通信网络涉密信息安全的动态预警。该方法没有对网络涉密信息作出聚类处理,导致预警耗费的时间长、效率低。
通信网络具有自身安全性的缺陷以及脆弱性、易受攻击性等,因此,通信双方用户的信息安全性逐渐成为通信网络可靠性控制的关键问题。为了进一步解决该问题,提出大规模通信网络涉密信息安全动态预警方法。
2 涉密信息聚类与异常检测
2.1 信息聚类
为了得到大规模通信网络中涉密信息的特征流量,采用模糊聚类算法对网络涉密信息做聚类处理[6],具体步骤如下:
1)模糊聚类算法通过计算网络涉密信息流量的最小代价函数来确定信息流量之间的相似关系,进而将具有相似特征的数据汇集到一起。公式如下所示

(1)
式中,K表示聚类表达数量;ϑ代表最小代价函数;e代表非相似性;M、N分别表示矩阵模型的长度与宽度;i、j均代表网络涉密信息流量;V表示矩阵模型。
2)大规模通信网络涉密信息安全的动态预警方法,引入拉格朗日函数[7]对最小代价函数求导,进而得到聚类表达合集,公式如下所示

(2)
其中,v表示聚类表达合集。
3)通过聚类表达合集对最小代价函数二次求导,得到如下公式

(3)
式中,β表示二次偏导数。
4)大规模通信网络涉密信息安全的动态预警方法,将式(2)与式(3)结合,得到矩阵模型与聚类表达集合的估计值,即为大规模通信网络涉密信息的流量特征。
2.2 异常检测
基于涉密信息的聚类结果,通过流量特征的样本均值与标准差设定一个固定阈值,然后将超过阈值的流量视为异常流量,具体步骤如下:
1)初始化大规模通信网络信息[8],假设任意时刻采集的网络涉密信息数据包长度是固定的,并且在这段时间内采集的网络涉密信息的时间长度也是固定的,则此刻网络涉密信息特征流量的固定阈值可用如下公式表示。

(4)
式中,U描述的是网络涉密信息特征流量的固定阈值;Δtl表示第l小时采集的网络涉密信息的时间长度;g表示起始时刻;len(t)代表数据包长度;t代表着任意时刻。


(5)
3)根据式(5)得到的样本均值,可以计算出第l小时网络涉密信息特征流量的样本标准差Rl,公式如下所示
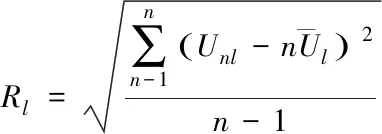
(6)
4)大规模通信网络涉密信息安全的动态预警方法,根据样本估计理论[9],采用涉密信息特征流量的样本均值与标准差代替网络整体的样本均值和标准差。引入样本均值与标准差的距离相关参数[10],则大规模通信网络涉密信息特征流量测量值maxUl可用如下公式表示。当流量测量值小于等于固定阈值时,表明此时的流量正常;当流量测量值大于固定阈值时,表明此时的流量处于异常状态。
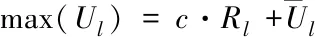
(7)
其中,c为特征流量样本均值与标准差的距离相关参数。
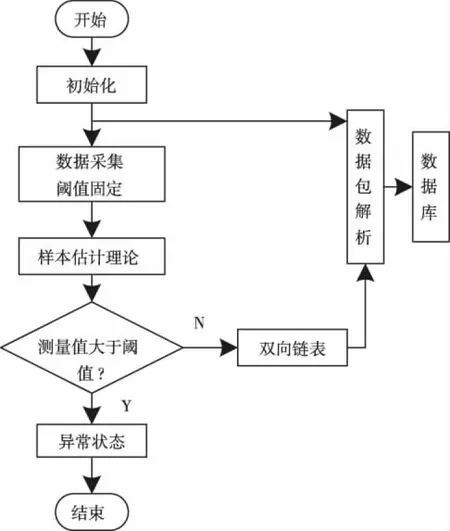
图1 样本估计流程图
3 网络涉密信息安全的动态预警方法
构建基于决策者互相评价的主观-客观综合赋权模型确定决策者的权重,然后采用妥协率算法对处于异常状态的网络涉密信息实行风险排序,完成动态预警,具体步骤如下:
1)针对大规模通信网络的多决策多属性问题[11],首先构造关于网络涉密信息属性的决策矩阵,公式如下所示

(8)
其中,m表示涉密信息属性的决策矩阵;a表示方案集合;b表示属性的个数;h表示决策者数量;i、j均表示网络涉密信息流量;ν代表属性集合。
2)为了消除网络信息分散化带来的量纲影响,采用极差变换法将决策矩阵规范法处理[12],规范化公式如下所示

(9)
式中,N代表规范化后的矩阵。
3)确定网络涉密信息的属性权重[13-14],然后根据属性权重推算出属性加权规范矩阵为
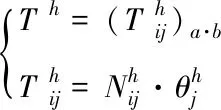
(10)
其中,T代表属性加权规范矩阵;θ为理想权重。
4)根据式(10)得到的属性加权规范矩阵,引入权重偏好系数,确定出决策者的主观综合权重与客观综合权重为:

(11)
式中,ϖ表示决策者的客观权重;χ代表决策者的主观权重;δ代表主观权重偏好系数;μ表示客观权重偏好系数。
5)利用加权平均算子[15]将步骤(4)得到的主观综合权重与客观综合权重相融合,得到主观-客观综合赋权模型Qij,可用如下公式表示。

(12)
6)在主观-客观综合赋权模型中寻找出正、负目标点。然后将正、负目标点代入到公式(9)中,得到各个决策者的所有方案,即为网络涉密信息流量的风险要素。将方案按照贴近度大小排序后,获得大规模通信网络涉密信息的风险评估结果,完成大规模通信网络信息安全的动态预警。
4 实验与分析
为了验证大规模通信网络涉密信息安全动态预警方法的整体有效性,需要对大规模通信网络涉密信息安全动态预警方法作出如下测试。将算法消耗的预警时间、预警准确率和误报率作为评价指标,采用大规模通信网络涉密信息安全动态预警方法、文献[4]提出的基于大数据采集的信息安全预警方法和文献[5]提出的基于层次分析法的信息安全预警方法完成对比测试。
4.1 耗时对比
通过不同方法检测1500组大规模通信网络涉密信息,对比不同方法消耗的预警时间。预警时间越长,说明算法的效率越低,相反,预警时间越短,说明算法的效率越高,不同方法的测试结果用表1表示。

表1 不同算法的预警时间
分析表1中的数据可知,针对大规模通信网络涉密信息安全的动态预警,研究方法的预警时间平均为12.47ms,基于大数据采集的信息安全预警方法和基于层次分析法的信息安全预警方法的预警平均耗时分别为36.27ms和45.47ms附近波动。通过对比可以发现,在不同实验序号下研究方法的预警时间均低于文献方法的预警时间,表明当前已有方法的预警效率远低于研究方法的预警效率。
4.2 准确率对比
设A表示各个算法的预警准确率,其计算公式如下所示

(13)
式中,p表示网络涉密信息样本集数量;I代表引入的检测函数。
利用所提方法、基于大数据采集的信息安全预警方法和基于层次分析法的信息安全预警方法检测五组大规模通信网络涉密信息,将不同方法的预警准确率结果绘制成柱形图,方便分析,如图2所示。

图2 不同方法的准确率测试结果
由图2可知,针对大规模通信网络涉密信息安全的动态预警,所提方法的预警准确率数值均高于文献方法的预警准确率数值。并且在不同实验序号下,所提方法的准确率数值比较稳定,没有发生明显变动。而已有传统方法的准确率数值上下波动较大。所提方法在对大规模通信网络涉密信息安全动态预警过程中,采用样本估计理论寻找出异常状态下的网络涉密信息区域,然后在这个范围中完成预警过程,进而提高了算法的准确率。
4.3 误报率对比
误报率是指在大规模通信网络涉密信息安全动态监测结果中,预警错误的信息量占总体信息量的比例。误报率越高,说明算法的预警精度越低;误报率越低,说明算法的预警精度越高,其计算公式如下所示
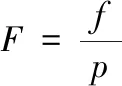
(14)
式中,F表示误报率;f表示误报事项数量。
将不同方法的误报率测试结果绘制成柱形图以完成对比分析,如图3所示。

图3 不同算法的误报率测试结果
分析图3可知,研究方法的误报率区间在5%以下;基于大数据采集的信息安全预警方法的误报率区间为50%至70%;基于层次分析法的信息安全预警方法的误报率区间为40%至70%。
5 结束语
针对目前大规模通信网络涉密信息安全的动态预警方法存在预警时间过长、预警准确率低、预警误报率高的问题,提出大规模通信网络涉密信息安全动态预警方法。利用模糊聚类算法对网络涉密信息作出聚类处理,结合样本估计理论寻找出具有异常状态的流量特征。最后采取妥协率法构建决策者模型,通过对异常流量的风险要素排序,完成大规模通信网络涉密信息安全的动态预警,降低了预警时间和误报率的同时,在一定程度上也提高了算法的预警准确率,为网络信息安全预警技术奠定了基础。

