融合精英学习与多项式变异的改进麻雀算法
欧阳城添,刘裕嘉,朱东林
(江西理工大学,江西 赣州 341000)
1 引言
群体智能优化算法主要是通过观察大自然中各种生物的群体觅食行为而发明的启发式算法。许多新型的群智能优化算法相继被提出,如:蚁群算法(Ant Colony Optimization,ACO),蝙蝠算法(Bat Algorithm,BA),蜻蜓算法(Dragonfly Algorithm,DA),鲸鱼优化算法(Whale Optimization algorithm,WOA),麻雀搜索算法(Sparrow Search Algortihm,SSA)等等。其中的麻雀搜索算法(SSA)是薛建凯等[1]在2020年首次提出的一种新型群体智能优化算法。麻雀搜索算法相较于其它算法有较好的优化效果[2],但在搜索过程中依旧存在效率较低和容易陷入局部最优的问题。
为对群体智能优化算法在搜索过程中的问题进行改善,许多学者都提出了自己的改善方案:康朝海等[3]提出一种基于精英高斯学习的改进鱼群粒子群混合算法,利用鱼群算法中较好的全局搜索能力和粒子群算法中较强的局部搜索能力的特点,在搜索初期利用鱼群算法来取得最佳群体,在迭代后期使用粒子群算法进行精确搜索,并在最后阶段采用改进的精英高斯学习策略,进一步优化最后结果的精度。杨万里等[4]提出一种基于Logistic映射的新型混沌简化PSO算法,引入混沌理论使惯性权重具有混沌搜索能力,同时使学习因子随寻优过程呈正弦函数变化,降低算法陷入局部最优的概率。黄清宝等[5]提出一种基于余弦控制因子和多项式变异的鲸鱼优化算法,利用余弦曲线和惯性权值优化控制参数,初期减缓收敛来增强全局搜索能力,后期加快收敛速度来优化搜索精度,并在最优鲸鱼位置上采用多项式变异,来使算法增加跳出局部极值的概率。卜冠南等[6]采用一种随迭代分组数减少策略方法,使蚁群算法增加全局搜索能力,提高求解路径规划性能。Wang W C等[7]引入柯西变异算子,避免萤火虫算法陷入局部最优,提高了全局搜寻能力。刘景森等[8]引入混沌映射和随机交叉策略,优化樽海鞘群算法的全局搜索性能,并将其应用于工程优化问题。
上述文献的改进方法,在一定程度上降低了算法陷入局部最优的概率,但在搜索过程中依然存在较大的随机性,实验结果并不总能满足优化预期。因此,在此基础之上,本文提出了融合精英学习与多项式变异的改进麻雀算法。在初始化阶段,利用维度空间均匀初始化种群,优化种群分布,提高初期搜索效率;然后在发现者搜索阶段,引入精英学习策略,扩大搜索范围,提高算法的开拓能力;最后在采用多项式变异对麻雀搜索算法中的最佳位置进行更新,降低算法陷入局部最优解的概率,增强寻优性能。通过8个基准函数的仿真,验证了上述方法的有效性。
2 麻雀搜索算法
在麻雀种群整个觅食过程中,自发地形成两种行为方式,一个为发现者,另一个为加入者。发现者的作用主要是引导种群发现觅食区域和具体方向,而加入者一般是在发现者的指引下获取食物。为了更大地提高自己的捕食概率,部分加入者会会对发现者进行监视而方便与其争夺食物或者围绕其周围进行觅食。当整个麻雀种群受到捕食者威胁时,会进行反捕食行为。
在SSA中,发现者会优先获得食物并比发现者获得更大的觅食范围。发现者一般占到种群的10%~20%,在每次迭代时位置更新公式如下

(1)
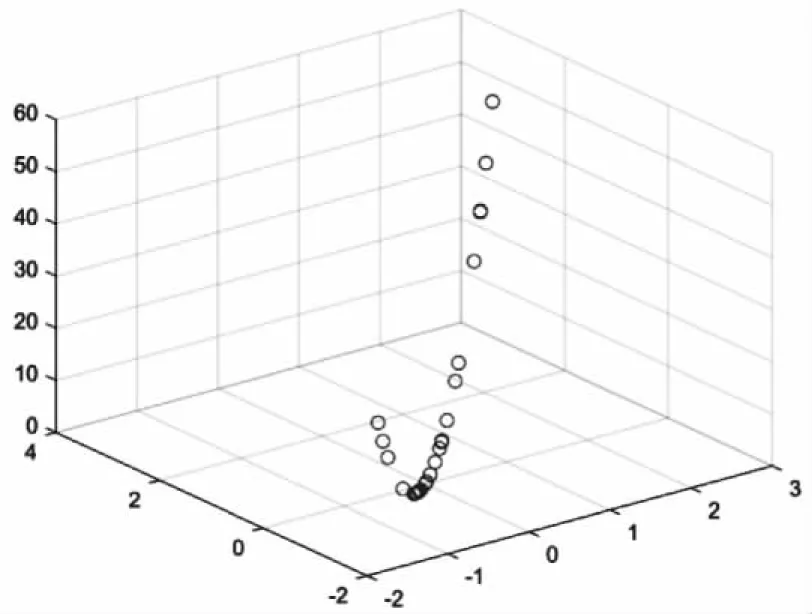
式中:t代表当前迭代次数;T为最大的迭代次数;Xi,j表示第i个麻雀在第j维中的位置信息。α∈(0,1]是一个随机数;Q是服从正态分布的随机数;L表示一个元素全为1的矩阵,大小为1×d,;R2∈[0,1]和ST∈[0.5,1]分别表示预警值和安全值。当R2 除了发现者,剩余的麻雀均作为加入者,并根据下式进行位置更新 (2) 式中:Xworst表示目前所在的全局最劣位置;Xp表示目前状态下发现者所处的最优位置;A表示一个1×d的矩阵,其中每个元素随机赋值为1或-1,并且A*=AT(AAT)-1。当i>n/2时,表示由于适应度较低,第i个加入者没有获取食物,处于非常饥饿的状态,所以需要飞往其它地方觅食来获取更高的能量。 当发现危险时,麻雀群会进行反捕食行为,其位置更新如下 (3) 式中:β表示步长控制参数,是服从均值为0,方差为1的正态分布随机数;K∈[-1,1]是一个随机数,表示麻雀移动的方向,同时也是步长控制参数;e设置为一个最小常数,来防止出现分母为0的情况;fi表示第i只麻雀的适应度值,fg和fw分别是当前种群的最优和最差适应度值。当fi>fg时,表明此麻雀位于种群的边缘,极容易受到捕食者袭击;当fi=fg时,表明种群中间的麻雀意识到捕食者的威胁,需要和其它麻雀一起抱团来减少被捕食的风险。 麻雀搜索算法在开始初始化过程中有较大的随机性,这将使得一部分的麻雀个体距离过近,空间上分布不均,从而将降低算法初期搜索效率。对此,本文将利用维度空间均匀初始化的方案来开始初始化麻雀种群。均匀初始化相对于Logistic混沌映射初始化和Tent映射初始化过程[9],所用时间更少并且约束条件更简单,种群分布更为均匀,并在算法初期的搜索效率也有进一步提升。以下为操作过程: 1)依据种群个体数目,种群个体在子空间中的密度系数ρ以及在每个维度分量的上限Xmax与下限Xmin,将麻雀种群所处的整个空间平均分成M个子空间。 2)在各个独立的子空间中,按任意概率产生出N个种群个体,根据 (4) 3)终初始种群由M×N个种群个体所构成,种群初始化过程就此结束。 麻雀种群中的发现者引导着种群的搜索方向和范围,所以发现者的搜索策略也直接影响了算法的寻优结果。在发现者搜索过程中,麻雀搜索算法自身的缺陷将有一定几率限制种群的觅食范围,致使最终落入局部极值的结果。 精英学习策略的目的是生成适应度高精英个体,获取精英解的位置,提高算法的寻优能力。本文做了一些改进,该策略的形成是受遗传算法和环形拓扑结构所启发,将遗传算法中的精英选择操作[10]和环形拓扑方法相结合,更多的筛选出引导能力较强的精英个体。 环形拓扑结构方程如下 qi,j=rj·xmi1,j+(1-rj)·xmi2,j (5) 引入的精英学习策略有效的扩展了发现者的搜索范围并优化了搜索路径,进一步增大了麻雀种群的觅食空间,增强了算法的全局探索能力和局部寻优能力,避免了陷入局部极值的困扰。 在智能优化算法的迭代过程中常容易陷入局部最优,而引入变异来降低算法陷入局部最优解的概率是一种行之有效的方法。在算法中加入变异算子有两点优势,首先,在迭代后期可以提高算法的求解速度;其次,也可以继续保持解的多样性。多项式变异[11]一般常被用于多目标函数优化,因为单目标优化也可以看作多目标优化的一种特别的情形,所以单目标优化也可以采用多项式变异进行操作。据此,本文引入多项式变异对麻雀搜索算法中的最佳个体位置进行优化选择 多项式变异算子方程式如下 vk+1=vk+δ×(uk-lk) (6) 其中 (7) u代表[0,1]内的任意数,分布指数为ηm,δ1=(vk-lk)/(uk-lk),δ2=(uk-vk)/(uk-lk),vk是初始最佳个体位置,vk+1是进行变异操作后的最佳个体位置,uk是位置上限,lk是位置下限。 在图书馆创客空间运动如火如荼开展的热潮中,学者们对创客空间建设的必要性进行了探讨,主要分为两种观点,一种观点认为建设创客空间非常必要,但也有学者从不同角度提出冷思考。 引入多项式变异算子,对麻雀最优位置进行更新变异,提高了算法跳出局部极值的概率,在搜索后期也进一步加快了算法收敛速度,增强了搜索效率。 本文提出的融合精英学习与多项式变异的改进麻雀算法,首先通过维度空间均匀初始化种群,均匀麻雀种群密度,提高初期搜索效率,接着采用精英学习策略,拓展发现者的搜索范围,增强算法的全局寻优能力,最后在麻雀最优位置引入多项式变异算子,进一步降低算法陷入局部最优解的概率,增强算法寻优性能。通过多策略的引入有效的改进了算法搜索能力的不足,在搜索效率和可靠性上有进一步增强,同时也提高了获得全局最优解的概率。具体步骤如下: 1)种群初始化。对种群数目,迭代次数和上下界进行初步设置。 2)通过维度空间均匀初始化种群,使麻雀位置重新进行分布。 3)计算各只麻雀的适应度值,找出当前最优适应度值和最差适应度值,以及相对应的位置。 4)从适应度值较优的麻雀中,选取部分麻雀作为发现者,按照式(5)更新位置。 5)余下麻雀作为跟随者,按照式(2)更新位置。 6)从麻雀中随机选择部分麻雀作为警戒者,按照式(3)更新位置。 7)选择多项式变异对当前最优解进行扰动,产生新解并进行对比,选取最优位置。 8)判断是否达到结束条件,若是,则进行下一步,否则跳转步骤2)。 9)程序结束,输出最优结果。 本文采用了8个标准测试函数来对ISSA算法的改进效果来进行分析验证,为进一步检验改进后的具体效果,加入了混沌麻雀搜索优化算法(CSSA)[12],原麻雀搜索算法(SSA),粒子群算法(PSO)与灰狼算法(GWO)进行对比实验。为了兼顾公平与效率,根据以往经验,所有算法的种群规模都设置为20,种群迭代次数为200。各个基准测试函数如表1。前6个函数维度设为30,单峰函数为F1-F4,多峰函数为F5-F6,剩余2个函数为不同定维函数。每个算法独立运行30次,计算出各算法的最优值、平均值、标准差。三项指标用来检验算法的寻优能力、寻优速度及稳定性。算法优化对比实验结果如表2。 表1 测试函数表 从表2的测试结果可以看出,相较于原算法,改进算法的寻优效果有显著性地提升,更容易找到最优解且求解效率更高。在前四个单峰测试函数中,ISSA算法地各个指标都相对很好,对比于其它算法在求解速度和精度上都有很好地效果,且更容易找到最优解;在中间两个多峰测试函数中,ISSA算法在F5函数上的表现有些许提升,在F6函数上提升效果更为明显,说明改进算法还是有一定的优化效果和稳定性。在最后两个定维测试函数中,ISSA算法在各方面的表现都比较突出,能更快更好的找到全局最优解,验证了改进的有效性。综合数据来看,CSSA算法的具有一定的改进效果,后面还有优化空间;PSO的指标数据不太稳定,寻优速度较慢;GWO寻优速度较快,但寻优精度极差,易陷入局部最优。由此可以看出,维度空间均匀初始化提升了算法初始的求解效率,精英学习策略和多项式变异的引入使得算法在摆脱局部极值的问题上有很好的改进效果。 为了清楚的表现出各个算法在不同测试函数的收敛效果,根据生成数据绘制了相关的算法收敛曲线。如图1所示,一共有8个基准测试函数的收敛曲线图,坐标中的横轴和纵轴分别表示迭代次数和适应度函数值。 图1 各算法收敛效果对比图 从对比图中可以看出,ISSA算法的收敛效果对比较为明显,在原有算法的基础上很大的提升,相比于其它算法,在收敛速度和稳定性上也具有很好的效果,更容易跳出局部极值的困扰。可以看出,改进方法的引入具有良好的优化效果,以上数据也进一步验证了改进方案的有效性。 仅凭最优值,平均值和标准差这三个指标不足以体现出ISSA算法与其它算法的优势,为兼具公平性,本文采用Wilcoxon秩检验的方法对于改进算法进行合理性评估。为了验证ISSA算法与其它算法是否具有显著的差异性,在P=0.05时对结果进行检验。如果P<0.05,可以认定为拒绝原假设,说明所对比的两种算法具有显著的差异性;如果P>0.05,就可以认定为接受其原假设,说明所对比的两种算法没有显著的差异性,也就是代表两种算法的优化效果相当,这里用N/A表示。具体结果如表3所示。 表3 Wilcoxon秩和检验P值 通过表3可以得知,ISSA算法与其它对比算法之间确实具有显著的差异性,也同时体现了改进算法的先进性。 为了更直观的展示改进算法的优化效果,分析检验策略的有效性,根据实验数据绘制了算法个体位置分布图。经过综合考虑,本文选用了F1测试函数对原算法和改进算法进行对比。图2和图3分别为SSA算法和ISSA算法的个体位置分布图。 图2 SSA算法个体分布图 图3 ISSA算法个体分布图 从图2可以看出,原算法的个体位置分布比较分散,个体收敛速度较慢,在个体寻优过程中不能快速有效的找到最优位置,寻优性能有待提升。 对比于图2,图3中改进算法的优化效果有明显提升。相比于原算法,改进算法的个体位置分布比较集中,个体收敛速度加快,说明所采用的维度空间初始化操作确实加快了种群的搜索效率,节约了时间。在个体寻优过程中,改进算法很快的找到了个体的最优位置,同时多数集中在最优区域,表明精英学习策略的有效性,也证明了多项式变异确实有效的提高了获得最优解的概率,增强了算法的性能。 智能算法的优化问题是算法研究的一大热点,在对麻雀搜索算法的研究中,为改善SSA算法的搜索效率和解决易陷入局部最优的问题,本文提出了融合精英学习与多项式变异的改进麻雀算法。首先,该算法利用了维度空间对种群进行均匀初始化,平衡了种群分布密度,提高了初期搜索效率;接着,通过引入精英学习策略改进了发现者的搜索方式,有效地提升了算法的全局搜索能力,使得搜索范围更加广阔;最后,多项式变异的引入对最优位置进行了选择性优化,提高了种群跳出局部最优的概率,增强了算法的寻优性能。通过算法性能测试分析可知,通过采用以上策略,有效地改善了麻雀搜索算法的搜索效率并且在一定程度上提高了算法的全局寻优能力,最终也进一步验证了ISSA算法的优化效果。在后面的研究中,将重点关注于把改进算法应用到工程实践中,发挥智能算法的优点。

3 改进的麻雀算法
3.1 均匀初始化

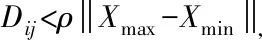
3.2 精英学习策略

3.3 多项式变异

3.4 改进的麻雀搜索算法流程
4 实验结果与分析
4.1 参数及环境设置

4.2 结果分析
4.3 算法收敛曲线对比分析

4.4 Wilcoxon秩和检验

4.5 策略有效性检验

4 结束语

