环境规制能否促进城市绿色创新?
邹伟勇
(上海大学 经济学院,上海 200444)
引 言
改革开放以来,我国快速推进工业化进程,取得了举世瞩目的成就。但经济的快速增长也带来了一定的环境污染,根据《2018年全球环境绩效指数》,中国空气质量在参评的180个国家和地区中位居倒数第4名,PM2.5等多项空气质量指标与国际排放标准存在一定差距。聚焦生态环境保护、推动经济社会可持续发展是中国式现代化应有之义。近年来,政府不断完善环境政策,推进生态文明建设,努力将外延式增长转变为内涵式增长。制定环境政策有利于改善生态环境,但监管也可能导致地方政府激励扭曲。在以经济增长为核心的“官员晋升”考核机制驱动下,地方政府为吸引资本和生产要素流入可能会降低环境标准,导致“逐底竞争”(刘华军 等,2019)。在新发展理念指引下,各地方政府政绩考核中纳入了环境质量指标。绿色创新作为环境监管与可持续发展的重要衔接点,已成为经济高质量发展的重要考量内容(余东华 等,2019)。有别于传统创新,绿色创新是企业高质量发展的重要措施,通过绿色技术研发和绿色产品生产,企业可以获得预期的环境和经济效益(薄文广 等,2018;张楠 等,2022)。
事实上,环境规制能否促进绿色创新仍存在不少争议,主要有“制约论”和“波特假说”两种观点。以新古典学派为代表的“制约论”认为,环境规制会降低生产者竞争力,提高生产者经营成本,降低生产者积极参与绿色创新研发活动的概率。这种观点也被称为“合规成本理论”,不少学者围绕该理论寻找了一系列的经验证据(李青原 等,2020)。然而,“波特假说”创造性地提出,严格但合理的环境规制标准可以促进生产者创新。庇古税、排污许可证等行政措施促使生产者内部化外部不经济行为,产生“创新补偿”效应以抵消合规成本影响,激励生产者参与绿色创新研发活动(Porter et al,1995)。后续的研究中,有较多学者围绕“波特假说”进行一系列的理论与经验探索(王馨 等,2021)。那么,环境规制对绿色创新是否产生显著影响?区域间存在异质性情况,环境政策如何因地制宜地实施?现有文献对该问题的内在作用机制探讨仍有不足之处,厘清上述问题,将为中国实施环境政策以促进绿色创新发展提供经验启示。
既有文献为本研究奠定了理论基础,并提供了逻辑起点。本文可能的边际贡献如下:一是囿于城市面板数据可得性问题,相关文献较少地从城市层面进行探讨。本文从城市的视角深入研究该问题,结合《政府工作报告》和国际专利分类清单等研究资料,科学衡量城市层面环境规制强度与绿色创新水平。二是以静态模型作为基准模型,并运用动态模型考察研究结论的长期适用性,丰富现有文献的经验证据。选取合适的工具变量,缓解模型互为因果和遗漏变量导致的内生性问题;运用空间计量模型,考察环境规制的城市绿色创新效应是否具有空间溢出效应。进一步强化异质性探讨,回答环境政策如何因地制宜实施的问题。三是现有文献对该问题的内在机制研究仍有待深入讨论,本研究通过引入传导机制模型和调节机制模型,以人力资本作为传导机制变量,市场化水平和财政研发支出作为调节机制变量,进一步完善机理分析。
一、研究机制与理论假说
环境规制有利于促进绿色创新,不仅源于创新补偿效应可以抵消合规成本,还源于节约经营成本、维持市场竞争优势和承担社会责任。首先,在节约成本上,企业不遵守环境规制的代价是高昂的。为避免由于高强度环境规制引起经营成本的增加,企业倾向做出改变,参与绿色工艺改进和技术研发活动(李春发 等,2021)。其次,在市场竞争上,企业面临环境法规的强制压力、客户和供应商等利益相关者的规范压力以及维持其市场份额的竞争压力等三类外部环境压力(Cai et al,2018)。在压力作用下,环境规制强度的提升将促使企业接受新思想,产品质量和环境绩效得到提高,获得市场竞争优势。最后,在承担社会责任上,企业为满足消费者和政府的环保需求进行转型,有利于企业获得社会责任感,树立良好的环保形象(赵爱武 等,2018)。
据此,提出本文理论假说1:环境规制可以提高城市绿色创新水平。
企业追求合规的行为取决于对外部知识的理解、吸收和商业化能力,而绿色创新行为增加组织灵活度以适应高强度的环境规制压力(Leblebici et al,1991)。环境监管是影响企业绿色创新的重要因素,环境执法不严格的地方容易成为企业的排污天堂。根据“波特假说”与“制约论”,提升环境规制强度有利于倒逼企业选择绿色创新策略,实现清洁生产,增强市场竞争力;而环境规制强度过大会产生较大的合规成本压力,则不利于企业进行绿色创新(Wang et al,2019)。因此,环境政策实施的力度需要把握适度原则。高绿色创新水平城市的企业拥有更优的绿色吸收能力,有机会获得政府给予更多的税收优惠待遇。适度提升环境规制强度将激励企业提高绿色创新投入,推动城市绿色转型(王娟茹 等,2018)。低绿色创新水平城市的企业难以识别、评估和利用新的市场机会,适度宽松的环境规制能够减少企业的合规成本,激发企业绿色创新活力,企业将更有意愿增加绿色创新投入,有利于城市绿色创新发展(Shen et al,2019)。
据此,提出本文理论假说2:在低环境规制强度城市和高绿色创新水平城市,适度提升环境规制强度有利于提升城市绿色创新水平。
在环境政策的压力下,城市中的企业将主动采取创新措施应对环境挑战。企业通过绿色绩效管理和薪酬管理整合生产资源,培养内部员工和引进创新型人才,鼓励员工产生新的想法和行动,有效提升组织人力资本水平(Ma et al,2019)。经过绿色培训和教育的员工有助于生产中提高绿色供应链管理水平,降低组织经营成本。高人力资本水平城市倾向使用绿色技术,引导产业绿色转型而有效地规避“资源诅咒”(潘楚林 等,2016)。高人力资本水平城市不仅有更强的技术吸引和扩散能力,还能推动新技术的应用和推广,而且具备有利条件激励人们接受环保理念和遵守环境法规(Bano et al,2018)。
据此,提出本文理论假说3:环境规制可以通过提升人力资本水平进而提高城市绿色创新水平。
市场机制能激发生产者的积极性,价格可以合理地反映资源稀缺性和产品供需情况,为生产配置提供合理指导。有效的市场促进跨区域竞争与合作,不仅能减少重复建设,还能通过兼并、收购和开拓新市场形成规模经济(Chen et al,2021)。生产者“以新求生”离开舒适区并提供新技术和产品,通过提高绿色技术改善经营业绩。以市场为基础的环保制度,如排污费、环境补贴、排放交易等环境政策,可以很好地将环境污染外部性内部化。通过降低边际污染治理成本,企业获得更多污染减排的激励补偿(Liao,2018)。相反,在不健全的市场机制下,产权不明确容易导致寻租和机会主义等行为,不利于城市绿色创新水平提升(Pan et al,2019)。
据此,提出本文理论假说4:较高的市场化发展程度可以强化环境规制对城市绿色创新水平的促进作用。
绿色创新是一种主动型的投资方式,具有投资周期长、资源投入大的特征。由于市场需求波动、关键技术人才变动和资金供给不足等原因,企业往往承担较大的绿色创新投入风险。若在绿色生产活动中付出努力但不能获得相应回报,企业则缺乏绿色创新投入的动力。不健全的市场定价体系容易产生“搭便车”行为倾向,仅靠市场的调节作用不足以促使城市绿色创新水平达到社会最优(Wang et al,2018)。财政研发支出对生产部门的研发活动产生积极影响,高效的公共研发系统能够更合理地运用私人研发资金,对城市绿色创新活动起着重要的作用。财政研发支出向市场发出信号,引导社会参与城市绿色创新活动,并为相关生产者缓解资金不足等问题,降低绿色研发成本和风险(Yi et al,2020)。
据此,提出本文理论假说5:较高的财政研发支出可以强化环境规制对城市绿色创新水平的促进作用。
二、研究设计
(一)模型构建
为考察环境规制对城市绿色创新水平的影响,本文构建如下基准回归模型:
lnGIit=α1+β1lnREGit+δ1lnXit+ui+vt+εit
(1)
其中,lnGIit为被解释变量,表示第i个城市t年的绿色创新水平。lnREGit为核心解释变量,表示第i个城市t年的环境规制强度,β1为本研究关注核心解释变量的估计系数。lnXit表示控制变量,本文选取人口密度水平、基础设施建设、外商投资水平和金融发展水平等控制变量。μi和vt为个体和时间固定效应,εit为残差项。
(二)指标选取
1.被解释变量
城市绿色创新水平(lnGI)。绿色创新是指“无公害化”“少公害化”的绿色技术,通过节约资源、降低能耗和减少环境污染排放以达到改善环境质量的目标。2010年世界知识产权组织(WIPO)推出便于检索环境友好型技术的国际专利分类绿色清单①,该检索条目依据《联合国气候变化框架公约》对绿色专利申请数分为能源节约类、替代能源生产类、交通运输类、废弃物管理类、行政监管与设计类、核电类和农林类七类。本研究根据上述划分依据,结合国家知识产权局专利分类号IPC信息进行匹配识别与核算,整理为衡量城市绿色创新水平的代理指标(陶峰 等,2021)。
2.核心解释变量
环境规制强度(lnREG)。目前,学界主要采用治污投资成本、污染物排放强度、污染税率和环保人员数等衡量环境规制强度。但上述方法仅反映政府治理环境的某方面,难以度量政府环境治理政策的全貌。为此,借鉴Chen等(2018)方法,选取各地级市《政府工作报告》中与环境相关词汇频数作为环境规制的代理变量。本研究采用Python软件并手工整理地方政府工作报告中与环境相关的词汇,检索相关的词频有:生态、环保、环境保护、减排、排污、空气、绿色、二氧化碳、污染、能耗、低碳、化学需氧量、二氧化硫、PM2.5、PM10等十五种。该指标具有更优的适用性,不仅很好地反映政府治理环境政策的全貌,还可以减少由于数据可得性问题的影响,降低传统方法对环境规制强度测度偏误。
图1显示2000—2019年环境词频数和绿色专利申请数的时序特征。环境词频数从2000年的287增长至2019年10464,年均增长率为25.12%。绿色专利申请数从2000年8058件增长至2019年的454224件,年均增长率为24.21%。环境相关词频数与城市绿色专利申请数具有相似的增长趋势,呈正相关关系。随着可持续发展理念深入人心,政府日益重视环保问题,环境规制强度的提升在一定程度上提升城市绿色创新水平。此外,环境词频数和绿色专利申请数在期末有增长放缓的迹象,可能的原因是:一是政府完善环境政策体系,适度提高环境规制强度有利于倒逼生产者参与绿色创新活动;二是我国逐步优化绿色专利结构,从重视专利数量向重视专利质量转变。
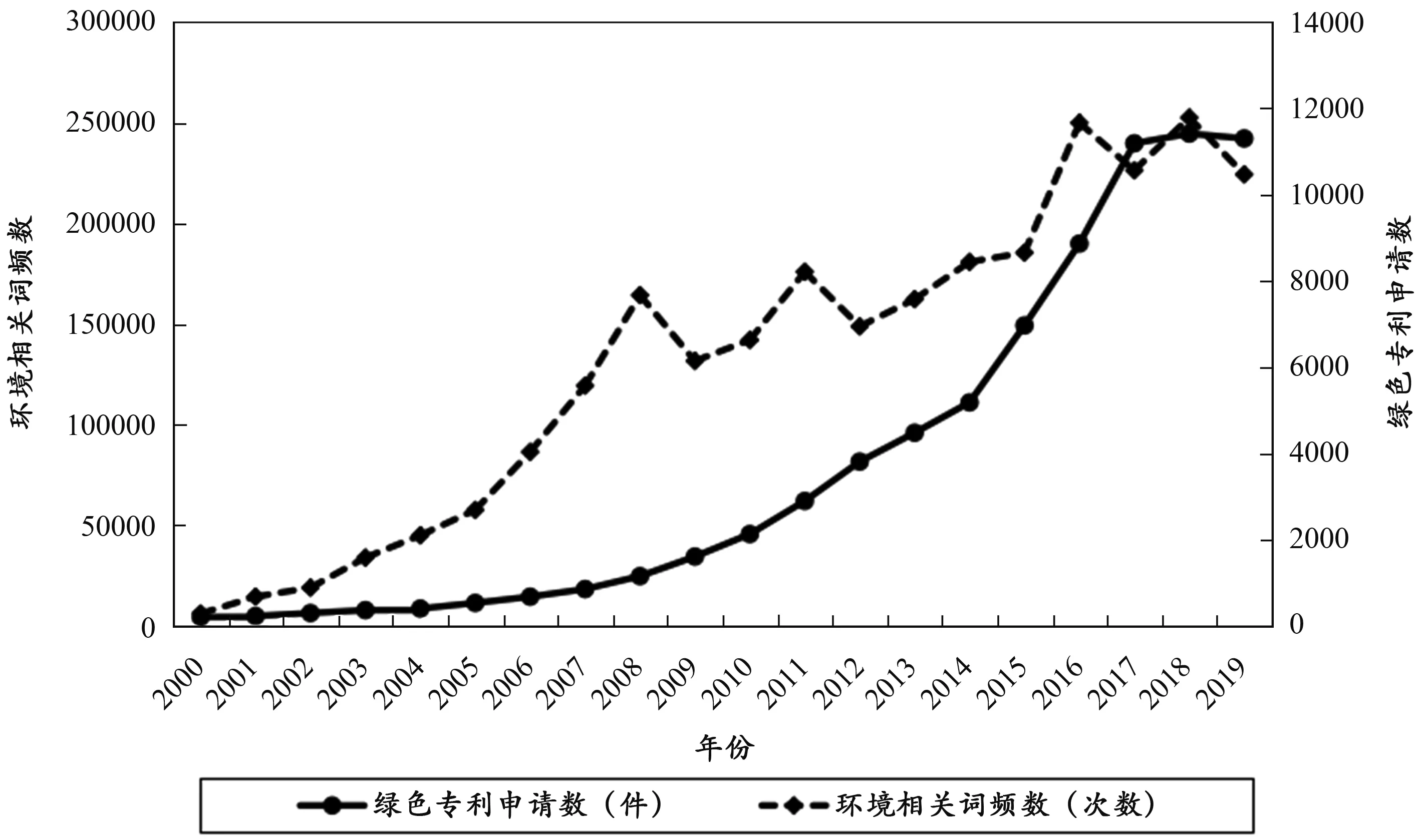
图1 环境词频数、绿色专利申请数的时序特征
3.机制变量
本文着重从人力资本的角度考察传导机制,采用每万在校大学生人数衡量人力资本(lnEdu)。从市场化水平和政府研发支出两个角度考察调节机制。采用私营和个体就业人数占总就业人数衡量市场化水平(lnMar),采用人均财政科技支出衡量财政研发支出程度(lnPte)。
4.工具变量
本文运用工具变量法缓解模型内生性问题,分别采用环境规制均值(lnPREG)、降水量(lnRain)、空气流通系数(lnVC)等作为环境规制的工具变量,工具变量的选择依据详见下文内生性分析部分。
5.控制变量
为更加准确评估环境规制的城市绿色创新效应,需要控制对城市绿色创新产生影响的因素。本文选取的控制变量如下:(1)人口密度水平(lnPop),用人口数除以行政区域面积衡量。(2)基础设施建设(lnInstra),用公路里程衡量。(3)外商投资水平(lnFdi),根据汇率将实际利用外资Fdi换算成人民币价格,再计算Fdi占GDP比重衡量。(4)金融发展水平(lnFin),用金融机构各项存贷款余额占GDP比重表示。
(三)数据来源
鉴于吐鲁番市、林芝市等城市缺失数据,故将其从样本剔除,最终选取2000—2019年中国285个城市共5700个样本数据。其中,城市绿色专利申请数来源于国家知识产权局以及国际专利绿色分类清单的标准匹配得出;环境规制数据来源于各地方《政府工作报告》;工具变量中的降水量来源于中国气象局气象科学数据共享平台;空气流通系数基于欧洲天气预报中心公布的ERA-Interim气象数据库。其余指标来自《中国城市统计年鉴》。此外,为减少数据异方差问题,样本数据均取对数作处理;部分缺失值则采用移动平均法等方法补齐数据。表1所示为主要变量的描述性统计。
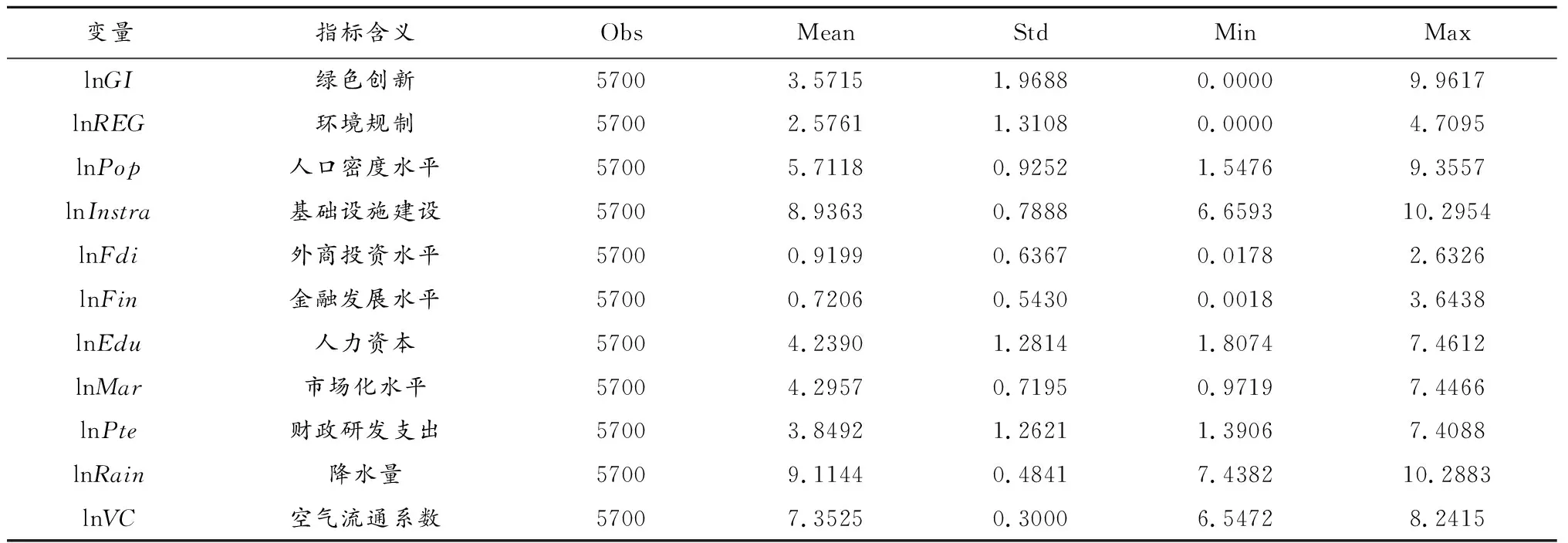
表1 主要变量描述性统计
三、回归结果分析
(一)基准回归
表2报告了基准回归结果,(1)~(3)列为静态面板模型,(4)~(6)列为纳入滞后一期被解释变量的动态面板模型,以检验研究结论是否具有长期稳健性。所有模型均引入城市和时间的固定效应。结果显示:短期内,lnREG的估计系数分别为0.2330、0.1564和0.0193,且分别通过1%、5%和10%的显著性水平检验。这意味着环境规制对城市绿色创新的促进作用在短期内是成立的。长期看,lnREG的估计系数分别为0.0802、0.0368和0.0171,且分别通过1%、1%和10%的显著性水平检验,说明环境规制对城市绿色创新具有显著持续的正向影响。无论是短期还是长期,环境规制始终有利于促进城市绿色创新发展,假说1得到了验证。此外,L.lnGI的估计系数分别为0.7385、0.8941和0.5021,且均通过1%显著性水平检验。这表明前期城市绿色创新水平对当期城市绿色创新水平具有显著的促进作用,城市绿色创新呈现“滚雪球”的动态影响效应。
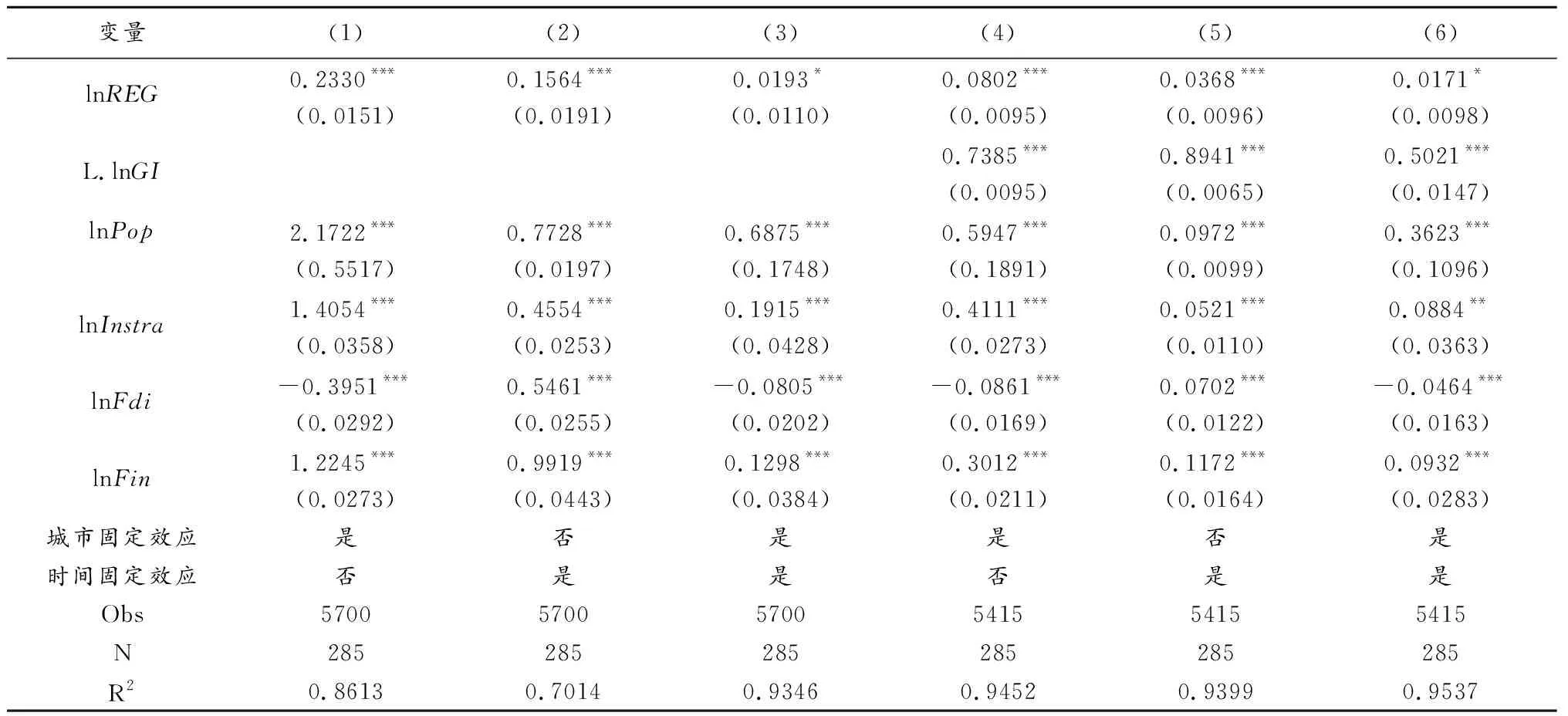
表2 基准回归模型结果
(二)内生性检验
由于城市绿色创新水平也会影响地方政府环境政策的制定,计量模型存在互为因果导致的内生性问题。同时,模型也可能存在遗漏变量的问题,导致估计结果偏误。借鉴Hering等(2014)的方法,本研究选取环境规制平均水平、降水量和空气流通系数②作为环境规制的工具变量,以缓解模型内生性问题。在环境规制平均水平的选择上,不同城市的环境规制平均值并不直接受到单个生产者行为影响,而环境规制的平均水平却与解释变量存在相关关系。降水量作为环境规制的工具变量,主要是由于降水有利于降低城市空气污染程度,减少污染扩散蔓延;同时降水属于自然现象,具有明显的外生性,其对城市绿色创新的作用仅通过环境规制来实现。空气流通系统作为环境规制的工具变量,是源于空气流通系数仅取决于区域的气候条件等自然现象,空气流通系数较低的城市倾向于执行严格的环境规制政策。空气流通系数除影响环境规制程度外,与城市绿色创新水平之间并不存在其他作用机制。因此,上述工具变量的选取均符合相关性与外生性假设要求。此外,由于环境规制平均值是截面数据形式,需要进一步处理成面板数据。借鉴Nunn等(2014)方法,本文引入每一年的时间虚拟变量与截面工具变量的交互项构建面板工具变量。
表3报告了两阶段最小二乘法的回归结果。(1)~(3)列分别以环境规制平均值(lnPREG)、降水量(lnRain)和空气流通系数(lnVC)等变量作为工具变量的回归模型。结果显示,LM统计量的P值均在1%显著水平上拒绝“工具变量识别不足”的原假设;F统计量大于Stock-Yogo弱识别检验10%水平上的临界值,说明工具变量构造是有效的。lnREG的估计系数分别为0.0831、0.0759和0.0710,且均通过5%的显著性水平检验。这表明在降低模型内生性后,基准回归结果仍然稳健。

表3 两阶段最小二乘法的估计结果
(三)空间效应检验
为加强模型稳健性的考察,并检验环境规制是否存在空间计量溢出效应,进一步利用空间模型进行分析。空间杜宾模型既考量自变量对因变量的影响情况,也考虑自变量对相邻地区因变量的影响关系,因此选取空间杜宾模型具有一般性。Hausman检验结果在1%显著水平下拒绝原假设,故选择固定效应模型更优。考虑到模型存在遗漏变量问题,因而选择时间和空间双固定效应模型,并纳入滞后一期被解释变量以考量动态影响。由于点回归结果不足以全面评估空间溢出效应,可能导致估计偏误,故本研究以空间杜宾分解模型作为分析重点。
空间模型分析之前,需要采用莫兰指数对核心指标进行空间自相关检验。从结果可知③,除初始个别年份外,绿色创新、环境规制的全局莫兰指数均通过了1%的置信水平检验,说明两者整体空间关联程度较高,可采用空间计量模型做进一步分析。表4报告了动态空间杜宾分解模型结果,其中,(1)~(3)列分别为直接效应模型、间接效应模型和总效应模型。结果显示,(1)~(2)列lnREG的估计系数分别为0.0462和0.1743,且分别通过1%和5%显著性水平检验。环境规制不仅显著地促进本地绿色创新水平,而且显著促进毗邻地区的城市绿色创新水平,说明环境规制的城市绿色创新效应具有空间溢出作用。随着生态文明建设逐步推进,政府在环境保护上战略互动频繁,有利于城市间绿色创新水平协同发展(李力 等,2021)。此外,模型空间滞后项ρ的估计系数为0.1587,且在1%显著性水平下显著。这说明城市绿色创新具有空间溢出效应,即城市绿色创新水平的提升,有利于带动周边城市绿色创新发展。

表4 动态空间杜宾分解模型结果
(四)异质性分析
不同城市环境规制强度和城市绿色创新水平存在异质性特征,需考察不同城市的环境规制强度对城市绿色创新水平影响的差异性。为验证这种差异是否存在,本文以环境规制和城市绿色创新的样本中位数为划分依据,研究样本分别划分为高、低两个等级环境规制强度与绿色创新水平。异质性检验结果如表5所示。结果显示,从环境规制强度的分区来看,第(1)列lnREG的估计系数为-0.0028,但不显著,表明在高环境规制强度城市中,保持适度宽松的环境规制强度有利于提升城市绿色创新水平。第(2)列lnREG的估计系数为0.0268,且通过10%显著性检验。这说明在低环境规制强度城市,政府可以适当提升环境规制强度以促进城市绿色创新水平。从绿色创新水平的分区来看,第(3)列lnREG的估计系数为0.0272,且通过10%显著性水平检验,说明在高绿色创新水平城市中,政府可以适当提升环境规制强度以促进城市绿色创新水平。第(4)列lnREG的估计系数为-0.0964,且通过1%显著性水平检验,表明在低绿色创新水平城市中,保持适度宽松的环境规制强度有利于提升城市绿色创新水平。因此,上述研究结论为假说2提供经验支持。
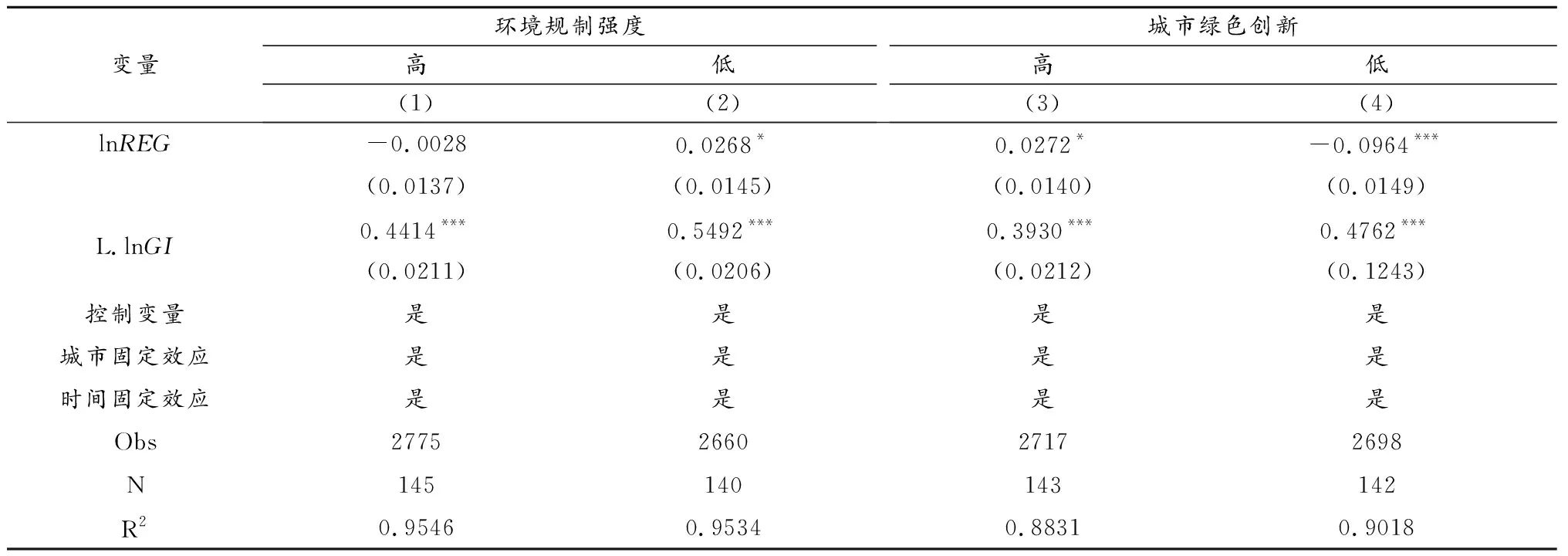
表5 异质性检验结果
四、进一步分析
为探析环境规制对城市绿色创新的影响机理,本文借鉴温忠麟等(2014)构建的传导机制和调节机制模型,识别环境规制对城市绿色创新的影响机理。机制模型构建如下:
Mit=α2+β2lnREGit+ρ2lnXit+ui+vt+εit
(2)
lnGIit=α3+ξ3lnGIit-1+β3lnREGit+ψ3Mit+ρ3lnXit+ui+vt+εit
(3)
lnGIit=α4+ξ4lnGIit-1+β4lnREGit+ω4Modit+ρ4lnXit+μi+νt+εit
(4)
lnGIit=α5+ξ5lnGIit-1+β5lnREGit+ω5Modit+η5lnREGit×Modit+ρ5lnXit+ui+vt+εit
(5)
传导机制过程如模型(2)和模型(3)所示,调节机制过程为模型(4)和模型(5)所示。其中,Mit为传导机制变量,本文选取人力资本(lnEduit)作为传导机制变量;Modit为调节机制变量,本文选取市场化水平(lnMarit)和财政研发支出(lnPteit)作为调节机制变量。
(一)传导机制检验
表6为人力资本的传导机制模型结果。Sobel检验的稳健标准误为0.1852,检验P值小于0.05,说明中介效应成立。第(1)列lnREG的估计系数为0.0236,且通过1%显著性水平检验,说明提升环境规制强度可以提升人力资本水平。第(2)列lnEdu的估计系数为0.0558,且通过1%显著性水平检验,说明提高人力资本水平有利于提升城市绿色创新水平。即人力资本是环境规制提升城市绿色创新水平的重要影响渠道,假说3得到检验。环境规制每提升1%个单位,人力资本提升0.0236%个单位,绿色创新提升0.0558%个单位,中介效应占比为7.7011%。环境规制强度趋严的条件下,企业更倾向于注重培养绿色创新型人才,人力资本水平的提高为促进城市绿色创新水平提供智力支持(杨明海 等,2021)。
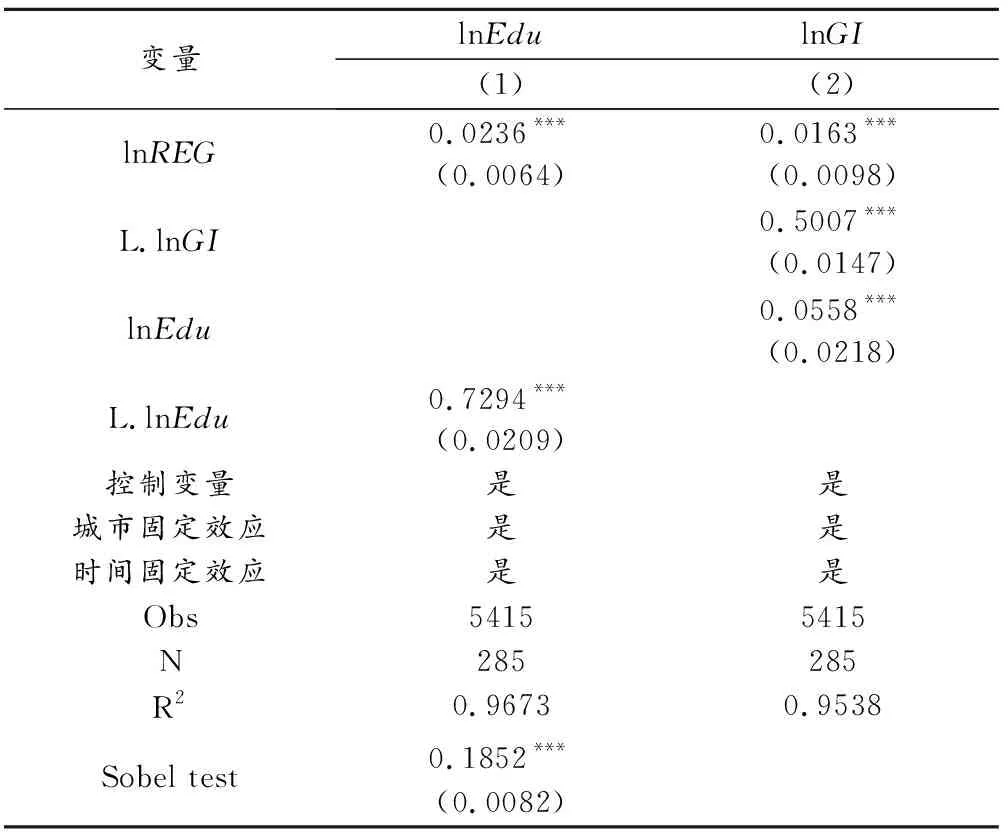
表6 人力资本的传导机制模型结果
(二)调节机制检验
表7报告市场化水平和财政研发支出的调节机制模型结果。第(1)列结果显示,市场化水平估计系数为0.0782,且通过1%显著性水平检验,说明提高市场化水平有利于提升城市绿色创新水平。第(2)列结果引入环境规制与市场化的交乘项,估计系数为0.0277,且通过1%显著性水平检验,说明市场化水平具有显著的正向调节作用,即较高的市场化程度强化了环境规制对城市绿色创新的促进作用,假说4得到了验证。市场化水平高意味着产品市场和要素市场发育程度相对较高。在开放的经济条件下,市场化程度越高越有利于优化城市资源配置效率,可以运用市场化手段来强化环境规制对城市绿色创新水平的促进作用。

表7 市场化水平和财政研发支出的调节机制模型结果
不少学者认为财政研发支出挤出了生产者投资,不利于提高城市绿色创新水平(王晓珍 等,2017)。但事实是否真的如此?本文进一步估计了财政研发支出在环境规制的绿色创新效应中的调节作用。表7第(3)列结果显示,lnPte的估计系数为0.3090,且通过1%显著性水平检验,说明财政研发支出有利于提升城市绿色创新水平。第(4)列结果引入环境规制与财政研发支出的交乘项,估计系数为0.0246,且通过1%显著性水平检验,说明财政研发支出具有显著的正向调节作用。较高的财政研发支出水平强化了环境规制对城市绿色创新水平的促进作用,假说5得到了验证。政府为生产者提供财政研发补贴支持,如采购先进设备和技术,培养研发人员开展绿色创新活动,可以缓解生产者绿色创新研发的融资约束,有利于提升城市绿色创新水平。
五、结论和政策建议
基于2000—2019年中国285个地级市的面板数据,本文分析了环境规制对城市绿色创新的影响及其机制。研究发现:(1)环境规制对城市绿色创新水平具有显著且持续的正向影响,该结果在工具变量法和空间杜宾分解模型的检验下仍具有稳健性。(2)由于不同城市其环境规制强度和城市绿色创新水平存在异质性特征,环境规制强度对城市绿色创新水平影响存在一定差异。在低环境规制强度城市和高绿色创新水平城市,适度提升环境规制强度有利于促进城市绿色创新。(3)机制检验发现,环境规制可以通过促进人力资本水平进而提升城市绿色创新水平;较高的市场化水平和财政研发支出程度可以强化环境规制对城市绿色创新水平的促进作用。
基于上述研究结果,本文提出以下政策建议:
第一,环境政策需要因地制宜,循序渐进。环境政策的落实需综合考虑当地现实情况,根据城市发展模式、资源禀赋等特征,采取合适的环境规制政策。如在环境执法不严和绿色创新水平较高的城市应适度提升环境规制力度。
第二,培育绿色人力资本,激发绿色创新活力。加强绿色人力资本管理的顶层设计,重视绿色人力资本细分领域的均衡发展。加强城市劳动力的环境知识和技能培训,利用数字化技术优化管理系统,提升绿色人力资本配置机制效率。
第三,有效市场和有为政府相结合。完善绿色技术要素市场成果转化的机制,支持企业牵头组建绿色创新联合体,鼓励大中小企业优化生产模式。政府加大对企业绿色攻关技术的研发投入支持,探索资助成果项目向发明人、中小企业转让和利益分配机制,强化财政研发支出对绿色创新引导的杠杆作用。
①http://www.wipo.int/classifications/ipc/en/est。
②空气流通系数等于风速乘以边界层高度。欧洲中期天气预报中心(ECMWF)的ERA-Interim数据库提供了全球0.75°×0.75°网格(大约83平方公里) 的10米高度风速(si10) 和边界层高度数据(blh)。
③由于篇幅原因,全局莫兰指数结果留存备索,空间矩阵选取0-1矩阵。

