适用于SCNN的多维度注意力方法

徐宇奇,王欣悦,徐小良

(杭州电子科技大学计算机学院,浙江 杭州 310018)

0 引 言

脉冲卷积神经网络(Spiking Convolutional Neural Network,SCNN)作为第三代神经网络中的分支,使用离散的脉冲信号进行信息传递,类似大脑皮层的信息处理方式使其具有巨大的发展潜力,成为神经形态视觉任务中的研究热点,在目标跟踪、图像识别与视频识别等领域应用广泛[1]。得益于脉冲传递的低耗能特性,SCNN还可以应用于边缘设备。与卷积神经网络(Convolutional Neural Network,CNN)不同,SCNN具有独特的时间维度,与通道、二维空间维度相结合形成了相当复杂的维度空间,大量的脉冲事件分布在复杂的网络空间内,增加了网络学习的压力,使神经元容易错误地关注到某些不重要的脉冲事件,在时间窗口内发放大量冗余脉冲,致使网络在增加计算量与能耗的同时,降低了后续神经元的可选择性,损害网络的信息表示[2-5]。相比于CNN,SCNN更需要多维度的注意力方法帮助网络对分布复杂化的脉冲事件作出精准的重要性判断。目前还没有专门适用于SCNN的多维度注意力方法来缓解上述问题。

在CNN中,有一种多维度的注意力方法(Convolutional Block Attention Module,CBAM)[6]可以通过压缩-提取模块获取特征图通道维度与二维空间维度的注意力并加以融合,快速聚焦于特征图的关键位置,但对于脉冲数据,CBAM无法考虑时间域范围内的全局性与多个样本间的全局性,并不适用于SCNN。因此,本文对CBAM进行改进,提出一种适用于SCNN的多维度注意力方法,使得神经元对各个脉冲事件的重要性作出精准的判断。

1 STBP学习算法

Wu等[5,7]提出了随时空域反向传播(Spatio-Temporal Backpropagation,STBP)学习算法,并与Pytorch框架兼容,将带泄漏整合发放(Leaky Integrate-And-Fire,LIF)神经元模型转换为显示迭代版本,快速训练更深层的脉冲神经网络。其膜电位u计算如下:

(1)

(2)

(3)

STBP学习算法使用近似导数来解决脉冲活动不可微问题。将瞬时的变化率近似为神经元在激活前一小段时间内的变化率,使用梯度下降算法进行误差的反向传播,近似导数如下:

(4)

式中,a为影响曲线宽窄的超参数。

2 SCNN多维度注意力方法

本文提出适用于SCNN的多维度注意力方法主要包括3个方面,分别为通道维度注意力的获取、时间维度注意力的获取、通道和时间与二维空间注意力的融合。

2.1 通道维度注意力

本文采用通道维度注意力(Channel Attention,CA)方法来获取SCNN中特征图V的通道维度注意力。首先,将特征图V的维度进行重新排列,获得通道维度在批次维度与时间维度下的全面信息;然后,通过卷积操作获取每个二维空间位置的重要性,对通道维度下的数据进行加权压缩;最后,通过全连接层获取全局信息通道维度的注意力。CA方法的步骤主要为批次-时间-通道整合、CA获取。

2.1.1 批次-时间-通道整合

为了使获取的通道注意力包含批次与时间维度的全局性,分别对V进行批次与通道维度、时间与通道维度的整合。假设1个尺寸为S×Ti×C×W×H的矩阵V,其中,S表示批次下的样本数,Ti表示包含当前时间点t=ti在内的前置时间点,即Ti∈{t1,t2,…,ti},C表示通道数,W与H表示二维宽和高。对处于当前时间点t=ti的V进行批次与通道维度的整合,将V沿S维度进行累加,矩阵尺寸由S×1×C×W×H变为1×C×W×H,记为矩阵A。此时,矩阵A携带了该批次的全局信息。

对V进行时间与通道维度的整合,将V沿前置时间点进行关于f(t)的加权相乘并累加,再经过函数g(x)进行激活,矩阵尺寸由1×Ti×C×W×H变为1×C×W×H,记为矩阵B,此时的矩阵B携带了前置时间点的全局信息。

(5)

(6)

(7)

2.1.2 通道维度注意力CA的获取与使用

将得到的矩阵A和B与当前样本在时间点t下的特征图Vt进行整合,得到的矩阵记为Ct。

Ct=λA+μB+ξVt

(8)

式中,矩阵A,B,Ct和Vt尺寸均为C×W×H。λ,μ,ξ为可学习参数,三者初始值相加为1,通过学习来确定矩阵A,B与Vt对矩阵Ct的贡献程度,并使其限制在±0.1。通道注意力CA的获取过程如图1所示。

图1 通道注意力CA获取示意图

对矩阵Ct进行双通道压缩操作时,直接使用MaxPool与AvgPool进行压缩并未考虑二维空间位置不同的重要性,存在一定的缺陷,故通过对矩阵Ct进行额外的卷积操作来获取全局二维空间的注意力。首先使用SoftMax与Sigmoid激活函数对卷积得到的数据进行激活,并将激活后的数据分别与矩阵Ct相乘,获得的矩阵记为D1与D2;然后,对D1进行AvgPool操作,对D2进行MaxPool操作,得到2个尺寸为C×1×1的矩阵。特别地,对于通过AvgPool得到的矩阵,将其中的每个元素乘以W×H,随后将2个尺寸为C×1×1的矩阵共同输入到1个共享的双层全连接感知机MLP={Fc1(C,C/r1),Fc2(C/r1,C)}中,其中C为通道维度,r1为超参数,Fc为全连接层。再将通过感知机MLP输出的2个矩阵相加后,通过ReLu激活函数进行激活,得到最终的多维度整合的通道注意力尺寸为C×1×1的矩阵CA,将CA与对应的Vt中通道维度的数据相乘即可使后续膜电位携带通道注意力。本文将由输入矩阵Ct到获取通道注意力的一系列操作记为ConvSE(Convolutional Squeeze Excitation)模块。

2.2 时间维度注意力

本文采用适合于SCNN的时间维度注意力方法(Temporal Attention,TA)来获取SCNN中特征图V的时间维度注意力。先通过转换迭代维度来获取所有时间点的信息,再由ConvSE模块获取时间维度注意力TA。

2.2.1 迭代维度转换

在STBP算法中,将LIF神经元模型定义为显式迭代的版本,具体实现中使用先层次后时间的迭代方法,即完成当前时刻下的网络前馈后,保存各层膜电位与各层输出数据,再进入下一个时间点进行前馈,直到遍历时间点结束。

若使用时间维度进行迭代,在经过卷积层后只能获取当前时间点之前的中间特征图,无法获取还未遍历到的时间点数据,导致网络无法获取每一层的完整时间维度的注意力。可进行迭代维度的转换来解决该问题。首先,将先层次后时间的迭代方法转换为先时间后层次迭代,忽略前置时间点的膜电位对后续时刻的影响,在每层(如第i层)获得所有时间点直接得到的中间特征图Vi;然后,使用Vi获取时间维度注意力,再进行后续的前置时间膜电位衰减加权,或进行发送脉冲后的超极化操作;最后,继续以上步骤进行层次上的迭代直到网络结束。

2.2.2 时间维度注意力TA的获取与使用

获取的第i层中间特征图Vi的尺寸为T×C×W×H,分别表示时间、通道、二维空间宽和高维度。通过对Vi进行2.1.2节所述的ConvSE操作,获取时间维度注意力TA,并将其迭代作用于膜电位的更新,如图2所示,具体步骤如下。

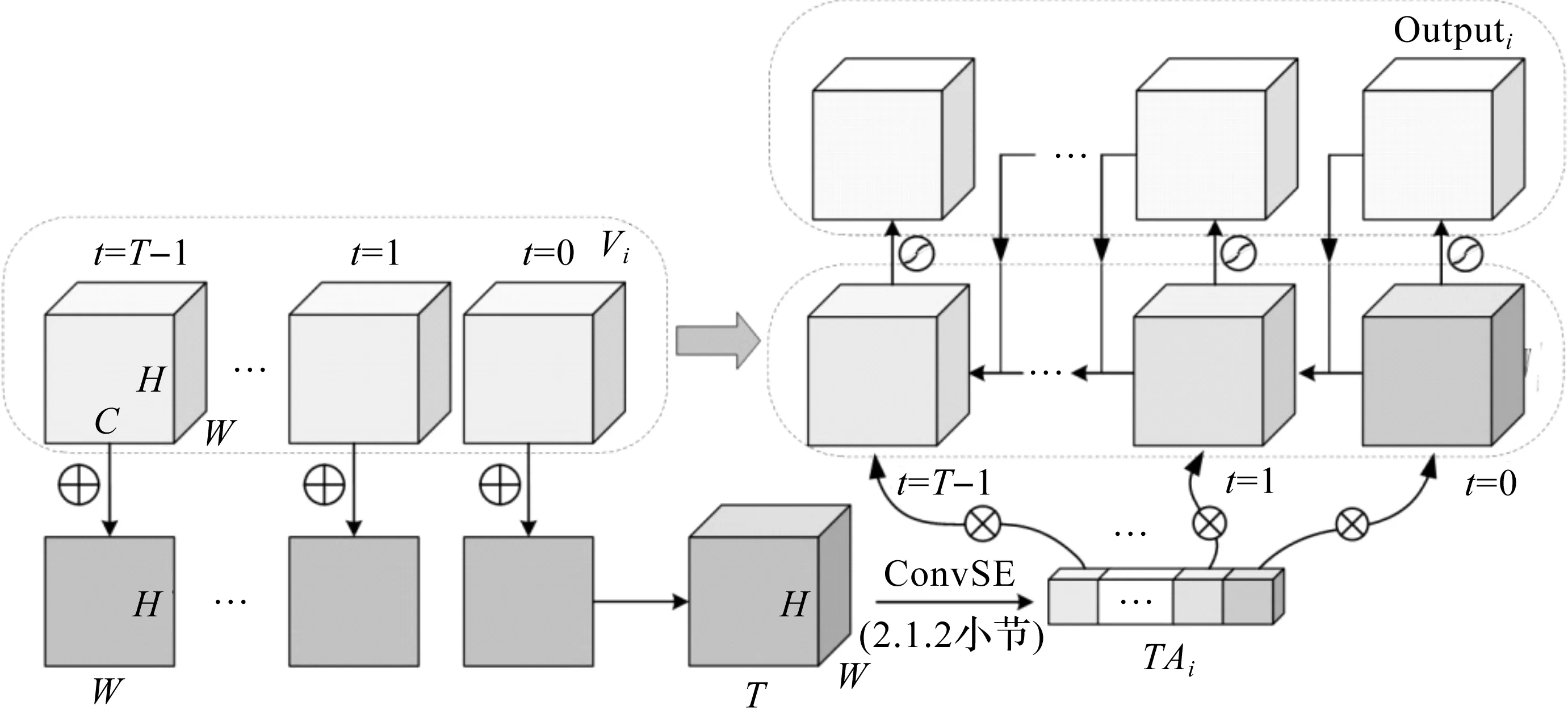
图2 TA的获取与作用示意图

(1)对所有时间点的中间特征图Vi进行通道维度的累加,尺寸变为T×W×H。

(2)针对步骤1获得的矩阵,使用结合了二维空间注意力的ConvSE模块,将其感知机MLP中的参数r1替换为r2,通过基于卷积操作的双路池化操作获取到时间维度上的注意力矩阵TAi,该矩阵大小为T×1×1。

2.3 多维度注意力融合策略

将通道维度注意力、时间维度注意力与在ConvSE模块中的二维空间维度注意力互相结合,形成适用于调整SCNN中神经元膜电位的多维度注意力方法。首先对迭代维度进行调整,获取第i层经过卷积后得到的所有时刻的中间特征图Vi,后续步骤如下。

本文提出的适用于SCNN的多维度注意力方法能将各个维度的注意力互相结合,使其形成相辅相成的关系以帮助网络更好地获取到在各个复杂维度下多维度有机融合的注意力分布,随着SCNN本身学习的进行,各个维度的注意力获取也在相应地进行调整,以达到适应网络的最好效果。

3 实验结果与分析

实验中,所有代码的实现均采用Python3.8,平台运行为PyCharm2020.2,服务器操作系统版本为Ubuntu18.04,CPU型号为Intel(R)Core(TM)i9-10900X,主频为3.70 GHz,GPU型号为RTX3090。实验数据集为3个神经形态数据集N-MNIST[8],CIFAR10-DVS[9]和DVS-Gesture[10],从识别精度、收敛速度、各维度注意力等方面来评估系统的性能。

3.1 数据集与实验环境

3.1.1 数据集

3个神经形态数据集中,N-MNIST和CIFAR10-DVS数据集上的时间窗口T=10,划分时间流时取间隔dt=10 ms;DVS-Gesture数据集上的时间窗口取T=40,dt=15 ms。

3.1.2 网络结构及参数设置

选用表1中的网络结构与具体参数,采用本文提出的适用于SCNN的多维度注意力方法分别在3个数据集上进行实验。

表1 实验数据集的网络结构表

表1中,128C3表示输出通道为128且卷积核尺寸为3×3的卷积层,AP2表示池化核尺寸为2×2的平均池化层,1024 FC表示输出数量为1 024的全连接层,VOTING表示分类层,Stride表示卷积核单次移动的步长。

3个数据集使用的参数与优化器如表2所示,其中,θ,A与k为STBP学习算法中的参数;λ,μ,ξ与r1为获取通道注意力CA时所使用的参数;τ,σ与r2为获取时间注意力TA时所使用的参数,优化器选择使用Adam[11]。

表2 实验数据集参数表

3.2 实验结果与分析

从识别精度、收敛速度与复杂度等方面对本文提出的适用于SCNN的多维度注意力方法(简称CTSA)进行评估和分析。

3.2.1 精度评估

分别对通道维度注意力CA、时间维度注意力TA、多维度注意力CTSA在3个数据集上进行识别精度的评估。结果如表3—表5所示,其中的“-comp”项为对比方法。

表3 CA精度评估

通道维度注意力CA、时间维度注意力TA与常规网络和对照方法(-comp组)的精度评估对比如表3所示,其中,CA-comp为不进行批次-通道与时间-通道的整合,直接对中间特征图进行压缩-提取以获得通道注意力,且在压缩时不考虑二维空间注意力;TA-comp为对输入数据直接进行压缩-提取操作获取注意力,且在压缩时不考虑的二维空间注意力。

表3与表4分别展示了CA,TA与常规网络和对照方法(-comp组)的精度评估对比,可以发现:尽管以往的通道与时间维度注意力(-comp组)的应用在每个数据集上都带来了一定的精度提升,但与本文方法对比,仍具有一定的差距。其中在N-MNIST与CIFAR10-DVS数据集上,CA比TA带来了更多的提升,这是因为这2个数据集将时间窗口大小T设置为10,与通道维度数量相差较大,CA取得了更好的效果;而在DVS-Gesture数据集上,T=40,时间维度极大延长后,使数据本身隐含了更多的时间维度的信息,给TA带来更大的发挥空间,TA的精度提升高于CA。

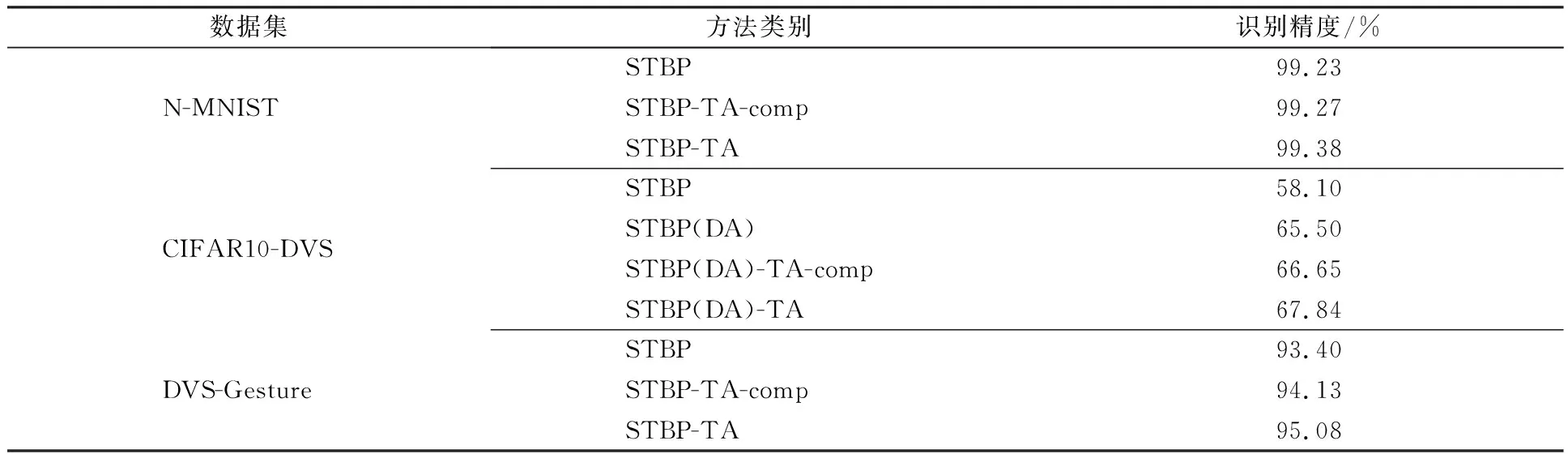
表4 TA精度评估

表5展示了通道维度注意力CA、时间维度注意力TA与多维度注意力CTSA在各个数据集上的识别精度,可以看出,在单维度注意力方法的基础上,CTSA进一步帮助SCNN提升了性能。

表5 CTSA精度评估

在CIFAR10-DVS数据集进行实验时发现,训练精度与测试精度相差较大,存在一定程度的过拟合现象,这是由于该数据集的复杂程度较高且数据量相对不足,导致网络泛化能力较低。针对以上问题,通过对图像进行裁剪、翻转等传统数据增强方法(Data Augmentation,DA)来提升训练数据的差异性,从而缓解过拟合现象[12]。在网络进行训练之前,本文先对CIFAR10-DVS的数据进行增强处理,对应表5中的STBP(DA)方法。如图3所示,首先,在128×128的图片上增加大小为24的padding,尺寸变为176×176,并将尺寸随机裁剪回128×128;然后,对图片进行随机的水平翻转。在此基础上,继续验证各注意力在CIFAR10-DVS数据集上的性能,实验结果表明,相比于经过数据增强的STBP算法,CTSA在该数据集上的识别精度提高了4.31%。

图3 CIFAR10-DVS数据增强流程图

3.2.2 收敛速度评估

为进一步探究各维度注意力方法为SCNN带来的性能提升,先采用CA与CA-comp、TA与TA-comp分别在3个数据集上进行收敛速度的对比,结果如图4所示,再对CA,TA与CTSA进行收敛速度的对比,结果如图5所示。其中normal曲线为只使用STBP算法的常规网络,图中横轴为迭代次数,纵轴为精度。

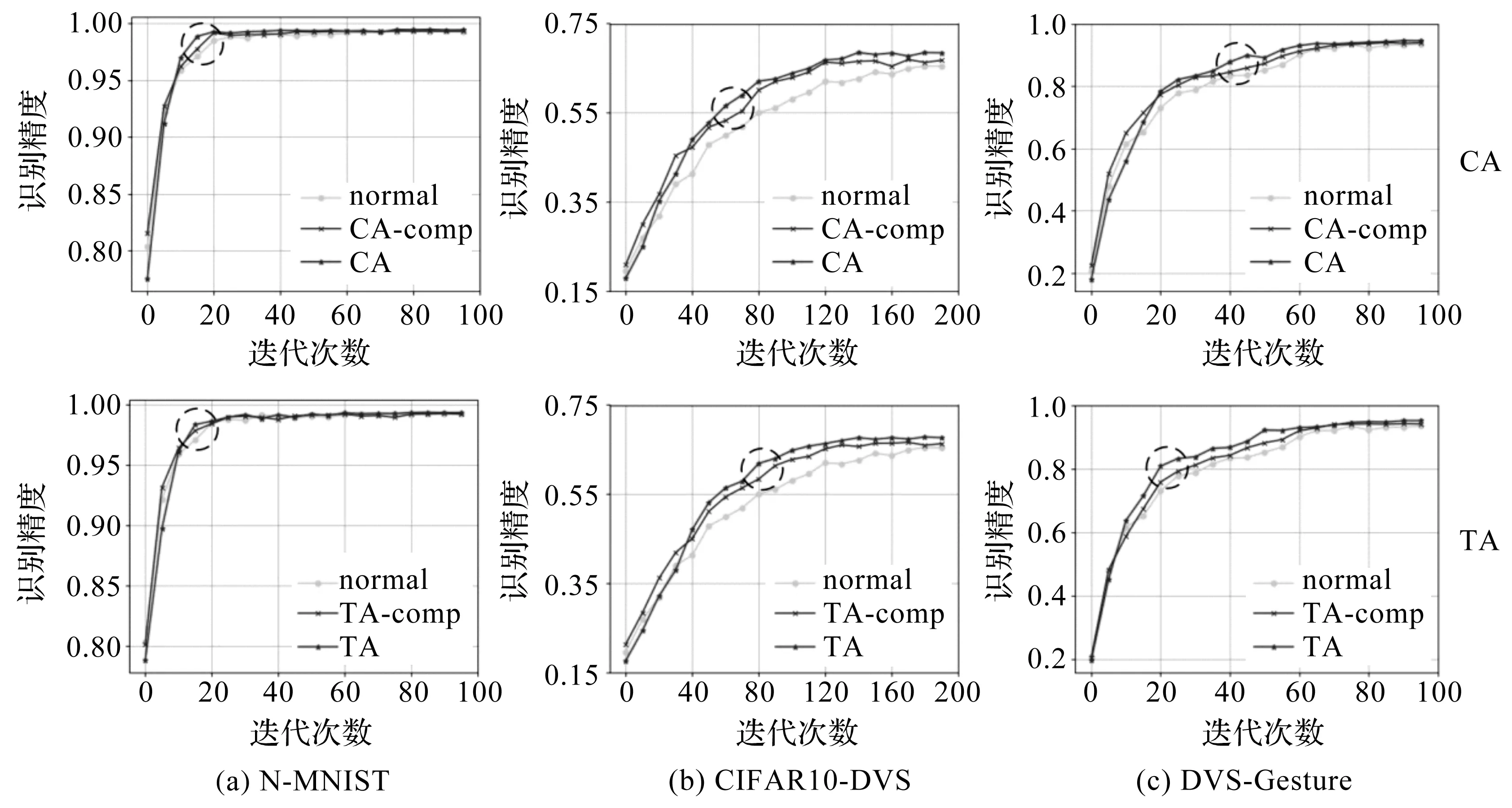
图4 单一维度注意力方法收敛速度对比

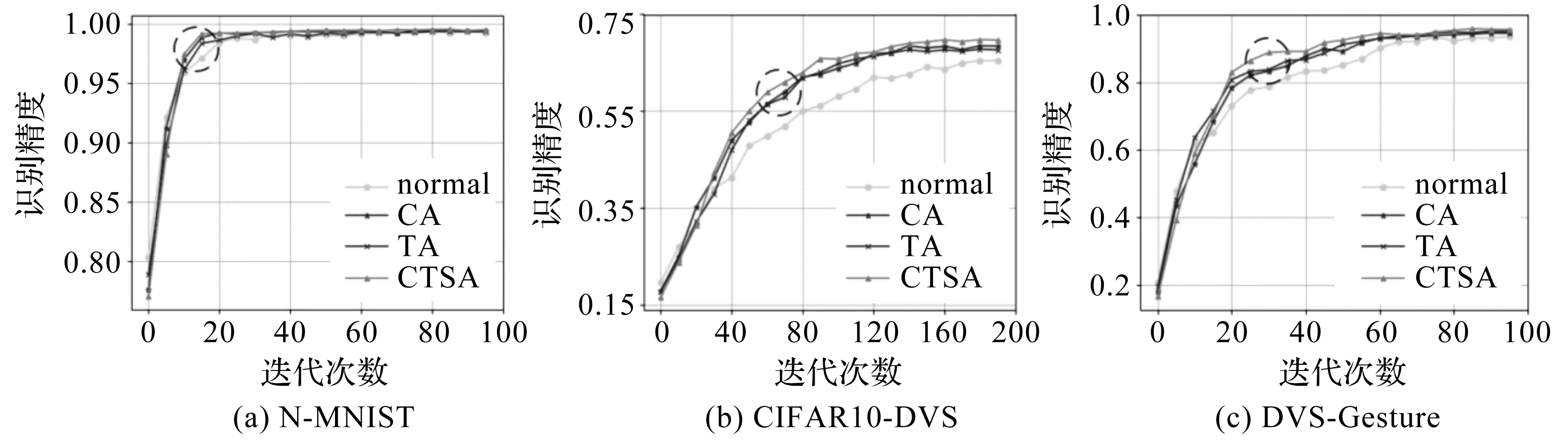
图5 CA,TA,CTSA收敛速度对比

从图4可以看出,和原网络与对照方法(-comp)相比,CA与TA均能更为快速地达到较高的精度,图中虚线圆圈标注的部分相差最大。前期精度上升速度略低于对照方法的主要原因在于本文方法整合了全局数据,且额外加入了卷积与全连接操作,在训练初始阶段更为困难,但最终均能快速地收敛到更高的精度。

从图5可以看出,在迭代过程的中期,多维度注意力方法CTSA与其他的单维度注意力方法逐渐拉开差距,最终以最小的迭代次数完成收敛。因为CTSA方法不局限于单个维度,而是将通道维度与时间维度的注意力有机结合,使两者相辅相成,在帮助网络提高精度的同时获得更快的收敛速度。

3.2.3 参数分析

对CTSA中参数λ,μ,ξ的默认值进行分析,将λ,μ限定在[0,0.3]之间,ξ随两者变化而变化,三者相加为1。每次变化步长为0.05,分别进行实验并使用精度评估。实验过程中,使用网格搜索方法[13-15]寻找最优的参数组。由于实验量较大,本文使用预训练与自训练联合的方法[16-17]进行,结果如图6所示。

图6 参数分析

从图6可以看出,在3个数据集上得到最好精度的λ,μ取值分别为(0.1,0.1),(0.15,0.15)与(0.1,0.15)。此外可以观察到,(0,0)附近的边缘位置与(0.3,0.3)边缘位置精度较低,前者主要是由于当λ,μ都为0或有某一个为0时,通道维度CA注意力失去了整合后的某些全局数据导致精度较低;后者是由于当λ,μ较大时,ξ取值较小,自身的原始信息传递效率过低导致精度下降。

3.2.4 注意力可视化展示

在网络收敛完全时,将3个数据集的CA矩阵与TA矩阵分别相乘,得到通道-时间二维位置的重要性,如图7所示,每个位置的重要性由暗到亮而递增。对于N-MNIST与CIFAR10-DVS,取时间维度全长进行展示;对于DVS-Gesture,从0开始每4个时间点选取1个用于展示。3个数据集的通道维度均取0～9,数据均取自于第1个卷积层。

图7 CA与TA融合重要性示意图

对比图7可以看出,DVS-Gesture数据集受时间维度的影响更为明显。这是因为DVS-Gesture数据集对时间维度会更为敏感,使用的是由DVS相机直接捕获的脉冲数据,而N-MNIST与CIFAR10-DVS数据集是通过基于帧的图片转换得到的。

3.2.5 复杂度分析

对CA,TA与CTSA进行时间与空间的复杂度分析。

(1)时间复杂度:对于CA方法,由于矩阵相加可并行操作,因此其中B-C,T-C整合与压缩提取过程均只需在每个时间点进行1次操作即可,每个步骤执行次数均为时间窗口的大小T,因此时间复杂度为O(n);对于TA方法,时间维度只需进行1次操作即可获取时间维度注意力,其时间复杂度为O(1);对于CTSA方法,将CA矩阵、TA矩阵与在TA方法中获得的SASA矩阵结合共同作用于每个时间点,复杂度为O(n);

(2)空间复杂度:从输入数据的角度分析,上述方法都在每个时间点产生了额外的中间变量,因此空间复杂度为O(n);从网络参数的角度分析,ConvSE模块中卷积层与2个全连接层所用参数远小于原始网络卷积层的参数,空间复杂度为O(1)。综上所述,CTSA方法的空间复杂度为O(n)。

4 结束语

本文提出一种适用于SCNN的多维度注意力方法。从全局视野出发,运用SCNN复杂的时空动力学,通过压缩-提取模块获取SCNN中特征图的通道、时间与二维空间维度注意力并加以融合,对分布在复杂时空维度下的各个脉冲事件作出更为精准的重要性判断,保证了网络信息的高效传输。但是,本文方法需要整合每个时间点的通道和批次,增加了一定的存储负担,计划继续挖掘时间维度与通道维度之间的共性,形成全局适用的注意力,减少存储空间的消耗。