基于可靠性约束的工作流调度算法
高一鸣,袁友伟,2,钱 逯
(1.杭州电子科技大学计算机学院,浙江 杭州 310018;2.浙江省脑机协同智能重点实验室,浙江 杭州 310018)
0 引 言
随着无线网络和物联网技术的快速发展,移动用户设备在网络边缘产生的数据量迅速增长,以云计算模型为核心的服务器端架构已无法满足当前网络环境对延迟、能耗等需求。移动边缘计算(Mobile Edge Computing, MEC)[1]是一种新的计算范式,通过建立一个在接近物理实体或服务源处提供服务的集成平台,使应用程序在边缘执行运算,以提高网络服务的响应速度[2-3]。在MEC环境中,边缘服务器节点可视作额外计算资源,移动设备将高计算需求任务传输至边缘服务器的过程称为计算卸载[4]。计算卸载将任务卸载至具有更高计算能力的边缘节点上,降低了任务的执行延时与设备能耗,弥补了移动设备本地计算能力不足的缺陷。但是,随着移动设备的增多和无线网络的日益复杂,现有的任务调度技术已无法满足调度的需求,不合理的调度方式往往造成更大的任务延时和传输能耗。改进的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ,NSGA Ⅱ)[5]是一种利用非支配排序对种群进行分级,通过计算种群个体间的拥挤距离得到近似解的算法。本文针对边缘用户的工作流信息、服务器可靠性、用户计算时延等信息进行建模,运用NSGA-Ⅱ算法生成最优的调度方案,提出一种基于可靠性约束的工作流调度(Workflow Scheduling)算法NSGA-Ⅱ-WS,在可靠性约束下,最小化工作流执行时延及能耗。
1 移动边缘计算系统模型
移动边缘计算系统模型主要包括工作流模型、可靠性模型、时间模型和能耗模型。
1.1 工作流模型
在移动边缘计算环境中,需要定义工作流和计算环境。用有向无环图表示工作流,工作流任务定义为w={V,E,wRD}。其中,V={t0,t1,…,tn}为任务集合,ti为工作流中的第i个任务;E={(tm,tn,tdm,n)|tm,tn∈V}为任务之间的边集,表示任务之间的依赖关系,tm为tn的前驱任务,tdm,n表示tm向tn传输数据集;wRD为该工作流的可靠性需求(Reliability Demand,RD)系数。工作流子任务的可靠性需求系数为tiRD,tiRD越大,任务ti的可靠性需求越高。φ(ti)={tk|(tk,ti,tk,i)∈E}为ti的所有前驱任务集合,φ(ti)={tk|(ti,tk,ti,k)∈E}为ti的后继任务集合。每个任务有3个属性ti={di,ci,oi},di,ci和oi分别表示输入数据、计算量和输出数据。此外,当前设备为1台本地服务器时,编号为0,MEC环境中可用边缘服务器数量为m,则可用服务器列表集合为S={s0,…,si…,sm}。
1.2 可靠性模型
移动边缘计算系统中,故障包含瞬时故障与永久故障。瞬时故障出现时间短且不会损害处理器,因此,本文仅将瞬时故障和可靠性结合在一起。一般来说,系统故障发生在设备通信与任务执行上,通信时间往往小于设备执行时间,因此,本文设计模型时,仅考虑处理器故障,不将通信故障纳入优化问题。在工作流应用中,任务在服务器上的执行可靠性通常与任务的执行时间和服务器的故障率有关,且任务的瞬态故障遵循泊松分布[6]。设λj为服务器sj的处理器每单元时间的恒定故障率,在时间间隔(0,τ]内,任务ti在服务器sj上执行的可靠性为:
R(ti,sj)=e-λjτ
(1)
用户设备可视为1个本地服务器,编号为0,当任务在本地设备上发生故障时,立即进行任务重启。若工作流w中的每个任务ti的调度位置已知,则工作流w的执行可靠性为:
(2)
式中,s(ti)为任务ti的执行位置。通过遍历服务器得到工作流w的最小可靠性值Rmin(w)和最大可靠性值Rmax(w)。对于R(w),势必存在约束0≤Rmin(w)≤R(w)≤Rmax(w)≤1,否则,执行方案不能满足工作流可靠性需求。当任务调度时,移动设备通过任务复制机制确保服务器故障时任务能够重新开始执行。
1.3 时间模型
在工作流调度过程中,任务完成时间包括任务的传输时间与执行时间。当用户设备选择将任务进行卸载时,μ时刻时,设备i向设备j数据传输速率trans(i,j)表示为:
(3)
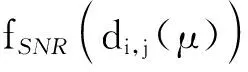
任务ti向服务器sj的传输时间为:
(4)
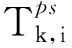
任务的执行时间与边缘节点性能和任务工作量有关,该任务的执行时间为:
(5)
式中,fj,k(ti)为服务器sj为ti提供的计算频率。
工作流w中的所有任务均完成,w才算完成。令l表示sj缓冲队列中的任务数,则工作流w的时延为:
(6)
1.4 能耗模型
在边缘计算环境中进行任务调度时,必然要考虑用户设备的能耗问题。用户设备的能耗主要包括本地执行任务产生的能耗和向其他边缘服务器传输数据产生的能耗。
对于工作流w,设本地设备计算功率为Pc,则本地执行能耗为:
(7)
式中,O为本地执行的任务集合。
设本地设备传输功率为Pt,工作流w通信产生的传输能耗为:
(8)

则设备总能耗为:
E=Eex(w)+Etrs(w)
(9)
2 基于可靠性约束的工作流调度算法
在改进NSGA-Ⅱ算法基础上,本文提出一种基于可靠性约束的工作流调度算法NSGA-Ⅱ-WS,在满足可靠性约束条件下,最小化设备的能耗和响应时间。
对于工作流w及其所有子任务V={t0,t1,…,tn},各任务可靠性需求系数tiRD∈[0,1],工作流可靠性需满足最低值,令{t0,t1,…,tj-1}表示已分配至满足可靠性约束的服务器或本地服务器的任务集合,{tj,tj+1,…,tn}表示未分配集合,Rgoal(w)表示工作流w的可靠性需求。当分配任务tj时,存在服务器满足条件Rj(w)≥Rgoal(w)。
定理对于工作流w中的每个任务tj,总能找到1个合适的服务器,且满足以下条件:
(10)
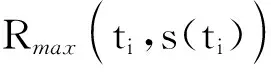
证明采用数学归纳法证明。在分配入口任务t0时,所有任务都未分配任务调度位置,应用程序w需要满足如下可靠性目标:
(11)
假设任务tj已经找到满足可靠性目标的可用服务器,则有:
(12)
同理,对于任务tj+1,其工作流执行可靠性为:
(13)
将式(13)代入式(12),可得:
(14)
所以,至少存在1个MEC服务器或者本地服务器满足Rgoal(w),即:
Rj+1(w)≥Rgoal(w)
(15)
对于工作流w中的每个任务tj总能找到1个合适的服务器来满足Rj(w)≥Rgoal(w)。证毕。
由定理可知,必定存在调度方案使得每个任务都能找到满足可靠性约束的服务器,再运用NSGA-Ⅱ-WS算法搜索满足可靠性约束条件下最优的工作流调度解。NSGA-Ⅱ-WS算法流程如图1所示。根据工作流信息初始化种群,采用选择、交叉、变异对种群进行更新,并运用精英策略筛选出种群中优秀个体,经过不断迭代得到最优种群。任务调度过程中若出现服务器故障,则重新执行NSGA-Ⅱ-WS算法。
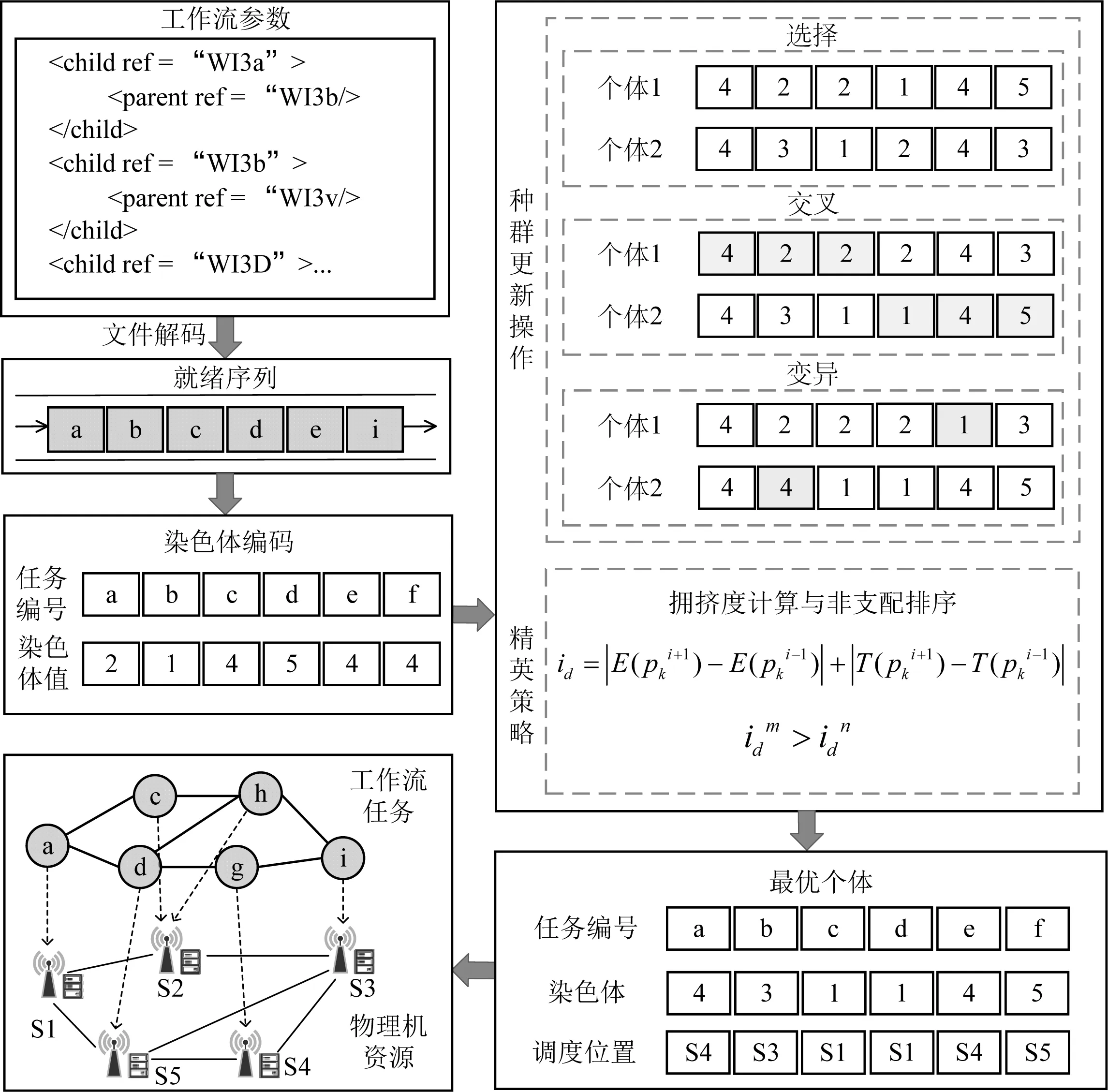
图1 NSGA-Ⅱ-WS算法执行流程示意图
将任务编号与服务器编号视为对应关系,每1条染色体代表1种MEC环境下工作流调度方案。假设存在工作流w,其子任务个数为n,移动边缘环境中服务器个数为m。染色体表示1个一维矩阵X,代表移动边缘计算环境下服务工作流调度问题的1个可行解,且染色体中的每个基因位都是正整数,X=[x0x1x2…xn],其中xi表示第i个任务的分配位置。
在正式初始化之前需要根据工作流子任务的优先级进行排序。使用随机法初始化任务调度位置与任务执行顺序,在[0,m]范围中生成1个随机数ri,若ri非整数,则对ri进行向下取整,将ri作为任务i所卸载的设备编号,生成相应的工作流调度方案,最终使用贪心策略生成初始化种群Pk={X1,X2,X3,…,XN},保证工作流调度方案的可靠性需求。
本文主要在移动边缘环境下实现一种基于可靠性约束的工作流调度算法,在满足可靠性约束的同时实现能耗和时延最小化。对于工作流w,优化目标函数表示为:
minαE+(1-α)T
s.t.T=T(w)
E=Eex(w)+Etrs(w)
0
(16)
式中,E为设备能耗,α为权重因子,T为工作流时延。优化目标函数在本模型中也被视为系统成本。选取该任务调度目标作为适应度评价指标,通过计算调度方案的适应度,评估调度方案的可靠性、时延与能耗,适应度值越小表示方案越优。该问题是一个NP-hard问题,需要在满足可靠性约束同时实现能耗和时延最小化。
本文提出的NSGA-Ⅱ-WS算法具体执行步骤如下。
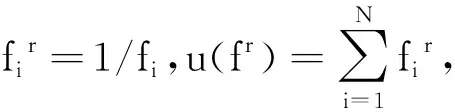
(2)交叉操作是算法优劣的关键。单点交叉算子选择位置效率较低,不能有效搜索解空间,故本文提出混合交叉算子。在单点交叉算子的基础上,随机在父代个体上选取q个不连续基因,对另一个交叉个体同位置基因进行交换,然后得到子代个体。基因的不连续性使父代与子代的差异性更大,从而扩大了解空间。
(3)变异操作扩大了工作流调度解的采样空间,增加了算法的搜索能力,避免工作流的解陷入局部最优。设置初始变异概率值为θ0,最大变化概率为ρ,最大迭代次数为ψ,当前迭代次数为k,变异概率计算公式为:
(17)
计算θN后,判断是否需要变异。若需要变异操作,则从种群中随机选取个体,对个体中的随机k个任务位置进行突变,至此得到子代种群Qk。
(4)精英策略将父代进行选择、交叉、变异后产生的子代混合得到混合种群Rk,并对Rk进行快速非支配排序,获取种群中的优秀个体并形成新的种群Nk+1,保证了工作流调度方案的鲁棒性与全局性。
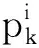
对第l支配层中的个体i计算拥挤度id,拥挤度表示每个个体周围个体的密度,具体计算公式为:
id=|E(pki+1)-E(pki-1)|+|T(pki+1)-T(pki-1)|
(18)
式中,E(pki+1)为在个体pki+1下调度所产生的能耗,T(pki+1)为在个体pki+1下调度所产生的任务延时,i-1,i+1表示前后个体。对于个体im与个体in,若idm>idn,则将im排在in之前。记第l非支配层中的个体数为z(l),种群Pk+1中当前的个体数为z(Pk+1),对第l非支配层中的所有个体进行拥挤度排序,取前z(l)-[z(Pk+1)-N]个个体,使种群Pk+1的规模变为N。
(5)判断是否符合结束条件,符合或者达到迭代次数则停止更新,返回工作流任务调度方案以及最优种群个体。不符合则k=k+1,返回步骤1继续迭代。
3 仿真实验与评估
3.1 实验环境与实验参数
为了更好地模拟工作流调度系统的运行模式,使用工作流生成器生成工作流,其中任务数量为10~100,任务数据大小为1~5 MB,计算需求为1~6 GHz,可靠性需求为0.6~0.9。边缘服务器的可靠性系数服从[0.999 00,0.999 99]的均匀分布,服务器个数为5~25,计算频率为5 GHz。用户设备带宽为10 MHz,传输速率为5 Mbps,计算频率为0~3 GHz,计算功耗为0.5 W,数据接受功率为50 mW,数据发射功率为100 mW,移动设备与服务器距离为0~200 m,信号干扰因子为-174 dbm/Hz,路径损耗常数为0.01,路径损耗指数为4[7]。实验中,NSGA-Ⅱ-WS算法的种群个数为100,最大迭代次数为400,初始变异概率θ0=0.5,最大变化概率ρ=0.3。优化目标中权重系数α为0.6。
选取本文的NSGA-Ⅱ-WS算法、轮询调度(Round Robin,RR)算法[8]、贪心算法Greedy和粒子群算法(Particle Swarm Optimization,PSO)[9]进行实验,其中,RR算法中,任务依次被均衡卸载到其他服务器节点;Greedy算法中,优先选择可靠性最高的服务器进行卸载;PSO算法将工作流调度方案初始化为一群随机粒子,在保证可靠性的同时,通过迭代获取粒子的最优解,得到最优的工作流调度方案。
3.2 不同可靠性约束下的性能
当可靠性约束系数tiRD分别为0.6和0.8时,采用4种算法进行实验,得到不同可靠性约束下的能耗如图2所示,平均时延如图3所示。
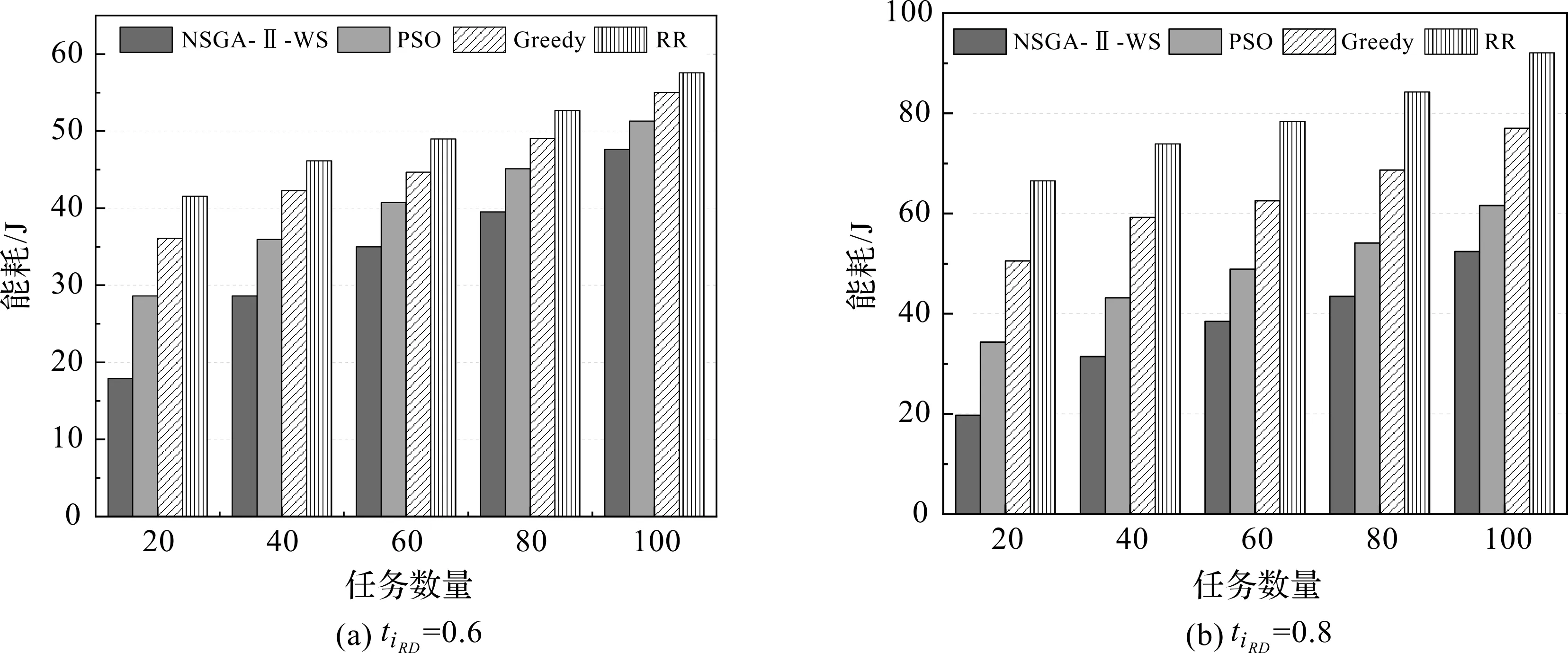
图2 不同可靠性约束下,任务数量和能耗的关系

图3 不同可靠性约束下,任务数量和平均延时的关系
从图2可以看出,随任务数量的增加,4种算法的能量消耗不断提升,其中,NSGA-Ⅱ-WS算法的能耗最小,因为NSGA-Ⅱ-WS算法生成调度序列时考虑了相同优先级任务的并行性,通过可靠性约束对交叉概率、变异概率以及精英策略进行自适应调整,使算法总能获得最佳的帕累托前沿,降低了工作流调度方案在可靠性约束下的能耗。
从图3可以看出,随着任务数量的增加,4种算法的工作流平均延迟也在增加。4种算法中,NSGA-Ⅱ-WS算法的平均延迟最低,因为NSGA-Ⅱ-WS算法将任务执行时间与能耗的加权和作为适应度进行迭代优化,缩短了平均延时。
3.3 系统成本
实验中,将系统成本定义为设备能耗与工作流时延基于权重系数α的加权和,当权重系数α=0.6时,采用4种算法进行实验,得到系统成本与任务数量和节点数量的关系如图4和图5所示。
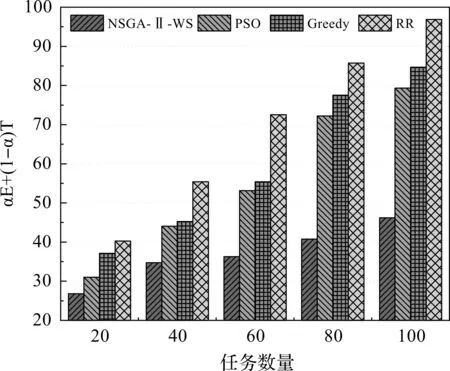
图4 任务数量和系统成本的关系
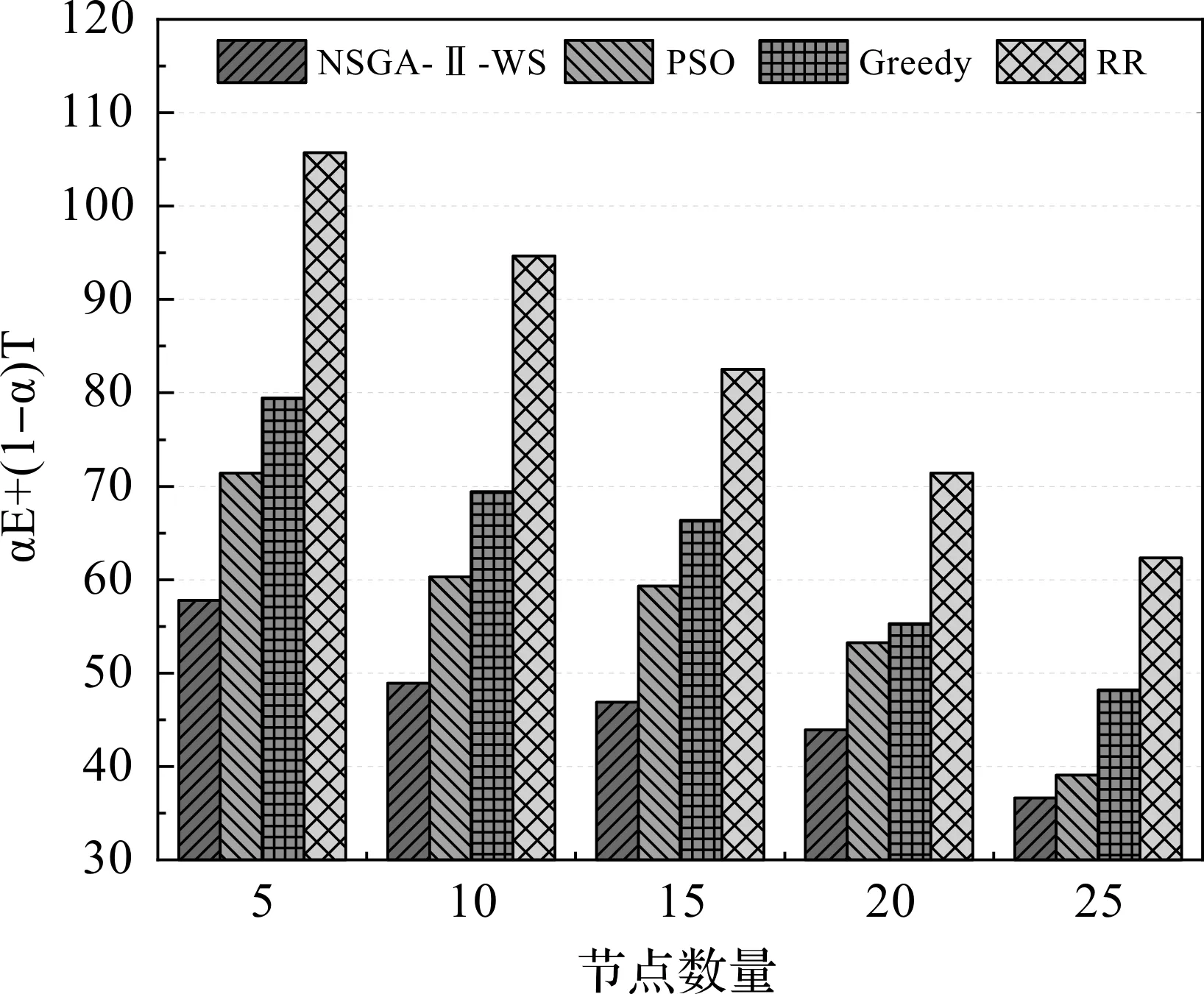
图5 服务器节点数和系统成本的关系
从图4可以看出,随着任务数量的增加,NSGA-Ⅱ-WS算法的优势逐渐显现,因为NSGA-Ⅱ-WS算法通过任务复制保证在故障发生时,能够调度至其他服务器继续执行,降低了故障损失。
从图5可以看出,NSGA-Ⅱ-WS算法具有更低的系统成本。因为NSGA-Ⅱ-WS算法通过基因变异和精英策略等手段生成足够优秀的调度解,将任务分配至合适的基站,使工作流调度方案在服务器节点较少时也具有更低的系统成本,满足可靠性的同时降低了能耗与任务执行时间。
为了探究不同优化权重系数α对NSGA-Ⅱ-WS算法的影响,本实验采用相同的工作流,通过改变优化权重系数α比较其能耗和时延,结果如图6所示。

图6 不同优化权重下系统成本对比
从图6可以看出,随着权重系数的增大,工作流调度方案中的用户能耗进一步降低,但工作流时延随之增加。随着优化函数中权重系数α的提高,为了得到适应度更低的个体,种群在搜索过程中会偏向能耗更低的个体。综上分析可知,可以通过改变权重系数α来迎合用户的不同偏好。
4 结束语
在保证工作流可靠性的基础上,充分考虑工作流任务对数据传输的依赖及不同服务器的故障率,采用改进的非支配排序遗传算法求解工作流的最优卸载位置,本文设计了一种基于可靠性约束的工作流调度算法,降低了移动设备的能耗,减少了任务时延,提高了工作流执行可靠性,保证了工作流调度方案的多样性与全局性。但是,本文在研究中未考虑边缘环境中服务器容量、负载状态和服务更替成本等指标,且未满足网络流量不断增长的需求与提升服务器及其他资源的利用效率,后续将针对服务器负载均衡等方面展开研究,实现在任务执行中各负载指标相互独立。

