基于UIF-MPC 仿真的UAV 环航姿态控制研究
朱代武,刘 豪,路东林,鲁 力
(1.中国民用航空飞行学院图书馆,四川 广汉 618307;2.中国民用航空飞行学院空中交通管理学院,四川 广汉 618307)
0 引言
对于分散、动态、多平台多元观测信息进行有效的态势融合,完成复杂环境感知和理解,是实现UAV 自主协同控制的必有举措;同时UAV 具有一定自治组织与协调能力,可通过控制器对其姿态、运动模式进行调整。UAV 控制系统主要依据任务进行飞行姿态调整,即需要实际飞行姿态与参考飞行姿态保持一致使得误差最小[1-2];ROTONDO D 等提出将非线性系统进行线性处理的变参数方法,虽然结构控制器比较简单但难以用于实际工程[3];KORKMAZ M 等提出比例积分微分控制办法,但处理数据过大响应时间过长,使得UAV 组织控制存在时滞[4];MELKOU L 等提出高阶滑模控制器,可有效减小偏振影响但牺牲该组织控制系统的鲁棒性[5];KARIMODDINI I、HAFEZ A T 及DENTLER J 等提出基于神经网络预测控制的UAV 姿态控制模型,但由于数据中心点的不确定性使得控制器最优化处理结果存在偏差[6-8];此外常用的控制算法如反步法[9-10]、模糊控制[11]、强化学习控制[12]等,但上述模型所需飞行数量量大,对未建模动态特性和未知干扰的适应性较差。因此,本文在考虑到UAV 时变系统的高度非线性、欠驱动、高耦合的特性[13-14]、外界环境的多变性与干扰性,提出一种UIF-MPC 仿真的UAV 环航姿态控制模型,使得UAV 在运动过程中具有较高的鲁棒性、抗干扰性与适应能力。
1 UAV 运动观测模型
假设目标运动场面环境为X-Y,UAV 定高飞行且速度大于目标移动速度,UAV 与运动目标体的相对运动如图1 所示。
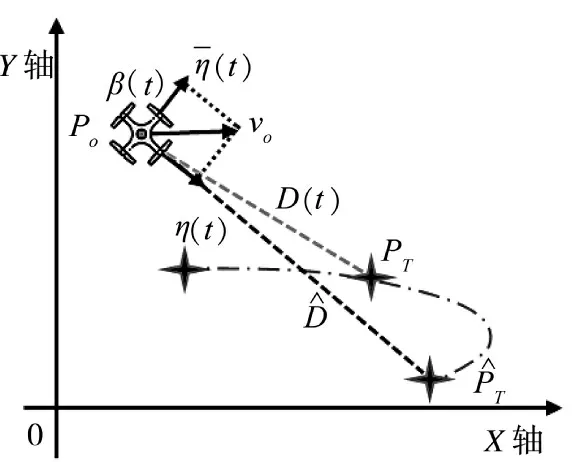
图1 无人机环航示意图Fig.1 Schematic diagram of UAV circumnavigation
其中,Po为UAV 位置;PT为目标位置;为目标估计位置;v0为UAV 的飞行速率;β(t)为测量角度;η(t)为UAV 与目标的测向矢量为η(t)逆时针旋转90°的向量;D(t)为两者之间的实际距离。
在对运动目标进行纯角度目标定位时,UAV 以目标作为圆心质点,以设定距离作为UAV 环巡半径飞行。因实际航迹与期望航迹存在误差,在实际操作中希望误差极限值趋于0,即极差差值收敛于坐标轴。UAV 的运动模型为:
令vo为该无人机的运动速率,Po=[xo,yo]T∈R2为UAV 位 置,PT=[xt,yt]T∈R2指 目 标 的 位 置,vo=[vocosαo,vosinαo]T∈R2为UAV 在X-Y 轴上的分速度,αo为UAV 航向,ωo为控制角速度。目标的运动模型为:
其中,vt为目标的运动,vt=[vtcosαt,vtsinαt]T∈R2为目标在X-Y 轴上的分速度;αt为目标航向;ωt为控制角速度。设UAV 与目标之间的相对速度为vr,则vr=vo-vt,根据式(2)~式(3)得相对运动方程为:
该运动方程下给出UAV 对目标进行环巡的控制策略。
在该策略中ed=d-Dd表示半径偏差;Dd为期望环航半径;β 为UAV 与目标之间的方向角;σ 为相对速度与传感器视线之间的夹角;为控制器参数。
基于成像传感器观测信息,目标被识别后可得到目标到UAV 的相对方位信息。对于非线性系统可根据噪声状态、状态转移参量以及量测函数对当前或者下一刻姿态进行估计[15],其模型如下:
式中,x[k]∈Rn表示k 时刻系统状态;z[k]∈Rm表示k 时刻测量数据;q[k-1]~N(0,Q[k-1])是k-1时刻过程噪声;r[k]~N(0,R[k])是k 时刻过程噪声;f 与h 为动态模型函数与测量函数模型,通过对当前状态估计,即
因在实际控制系统中假设系统模型随时间改变,变化的系统特性很难通过固定模型进行描述,因此,在估计中需考虑系统模型改变的可能性[16]。假设当前模型由M 个离散子模型集合f={f1,f2,…,fM},则式(6)可改写为:
假设对每个状态转移子模型都有一个预先的概率μj[0]=P{fj[0]},且在下一时刻从模型i 到模型j的切换概率已知,记为pij=P{fj[K]|fj[K-1]}。考虑到目标函数的多模态特性,可对式(8)进行改进。
2 MPC 下运动观测模型构建
模型预测控制(model predictive control,MPC)适应于优化和控制两个领域的交叉工程。该模型善于处理多输入多输出系统,且对于UAV 控制系统存在耦合关系或者系统过于冗杂的问题可通过MPC进行多控制变量的交互;且MPC 可将先验信息及未来参考信息纳入控制优化以改善控制器的性能,其多信道传输和交互性如图2 所示。
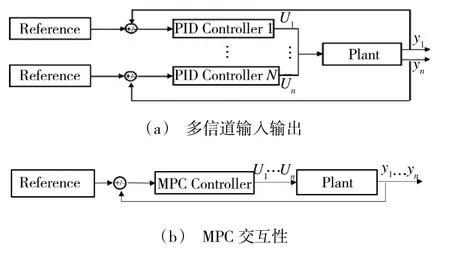
图2 MPC 模型预测控制特性Fig.2 MPC model predicts control characteristics
MPC 可以提前考虑UAV 控制器及飞行性能,从而可以提供更好的环航体验,对UAV 环航运动进行改进,改进后如图3 所示。
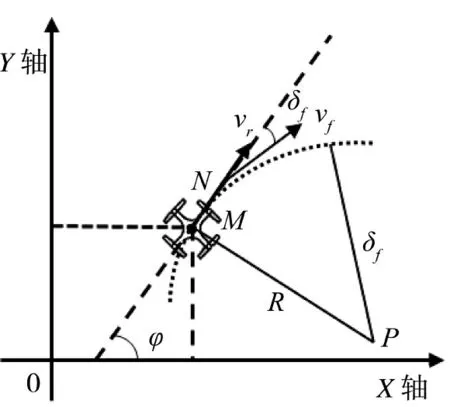
图3 基于MPC 的UAV 转向示意图Fig.3 Schematic diagram of an MPC-based UAV steering
其中,φ 为航向角;δf为UAV 前旋转轴偏角;vr和vf为旋翼前轴与后轴的实时测定的速度;R 为相对于目标的转向半径;P 为UAV 的瞬时转动速度;M 为UAV 后旋翼质点;N 为UAV 后旋翼质点。在后旋翼轴心(xr,yr)处,速度可分解为横纵坐标变化率分量的叠加,且UAV 垂直于自身的瞬时速度为0。
定义摆角速度ω=φ,并根据正弦余弦展开公式进行联合的MPC 得运动模型,令UAV 的状态变量为(x,y,φ),(v,δ)为控制输入。
此时环航的UAV 可以看作一个输入χ(x,y,φ)与u(v,δ)的控制系统,即S=f(χ,u)。UAV 的环巡参考运动轨迹形式采用泰勒级别展开(忽略高阶项)的线性化得UAV 误差模型。
上述线性化的UAV 模型是连续的,需要对其进行离散化处理,才可由当前时刻的状态量误差和控制量误差推导到下一刻的状态量误差,离散化为
由于状态量偏差不要求全输出,所以定义输出方程。
因UAV 环航运动模型由M 个离散子模型集合f={f1,f2,…,fM},令M=Nu,则输出方程为,
其中,ξ(k)与Δu 为当前时刻的状态量和控制时域内的增量。
3 基于UIF 的MPC 融合估计结构模型
观测对UAV 状态信息和时域增量信息产生的贡献与状态似然函数相关,假设传感器满足独立分布特征,即可得到运动姿态信息融合滤波[17]。在该融合结构中将信息状态y 与Y 可以写成:
式中,ii[k]与Ii[k]分别为传感器在k 时刻的观测对信息状态与信息矩阵的贡献,其集中式融合结构如图4 所示。
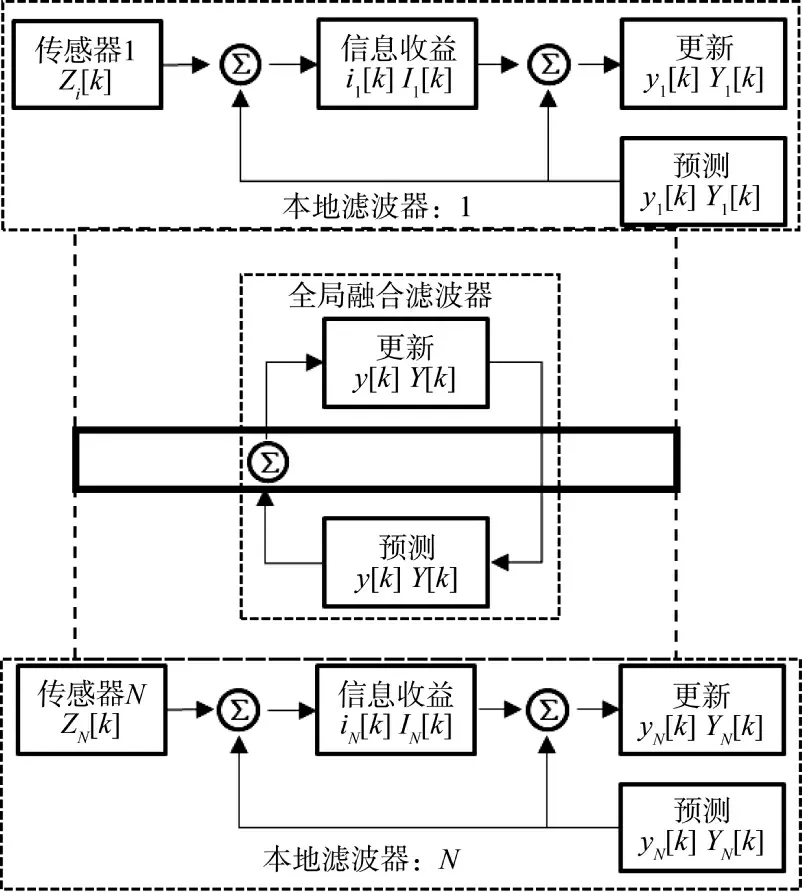
图4 基于UIF 的集中融合预测结构Fig.4 Centralized fusion prediction structure based on UIF
简单的特性相加使得信息滤波在多传感器融合估计中较为简单实用。各传感器节点只需要产生信息项Ii[k]与ii[k]在全局融合滤波器中进行相加便可以得到全局融合姿态估计[18-19]。当UAV 感知对象为多子模型的移动目标时可以将MPC 方法用于融合滤波中。在图4 中可以同时在局部滤波器与中心滤波器中利用MPC-UIF。通过计算信息收益对环航姿态进行评估,对应信息收益公式为,
综上所述基于MPC-UIF 的融合估计算法整体流程如图5 所示。

图5 基于MPC-UIF 融合估计算法流程Fig.5 Flow of estimation algorithm based on MPC-UIF fusion
4 仿真分析
针对UAV 跟踪单运动目标的任务进行仿真实验,假定目标在2D 平面内运动记为x=[x,y,x1,y1,φ,φ1],UAV 的初始位置为[-25,0];其飞行速率为20 m/s,期望环航半径为Dd=1km,k1=0.1,k2=0.01,α=0.6,γ=5,ξ=2,σ=0.001。其中,φ 表示目标运动方向,运动目标初始状态设定如下:
在win10 的运行环境下进行UAV 协同仿真,同时采用MATLAB2018.a 进行模拟仿真实现。下页图6 为环航跟踪的轨迹图,红色实线为目标运动物体,图7 为在X/Y 方向的位置估计误差。通过图7 可以看出,融合算法的x,y 方向估计误差波峰区间为[-10,10],远小于单纯UIF 算法的峰值[-25,25],说明MPC-UIF 融合预测能够在较小误差下完成对目标的位置估计并完成跟踪,且跟踪效果良好。
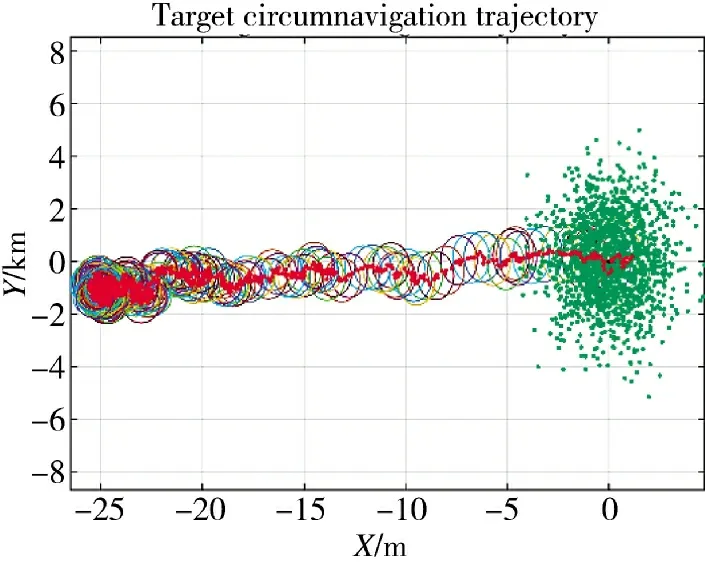
图6 目标环航轨迹图Fig.6 Target circumnavigation trajectory diagram
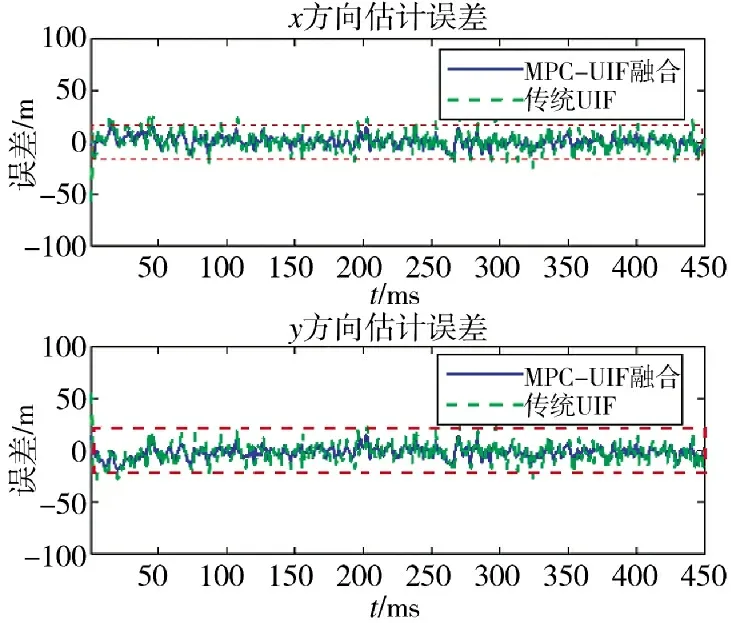
图7 位置估计误差Fig.7 Position estimation error
本文中目标初始位置为[-25,0],终点目标位置为[0,0]。UAV 在对目标环航过程中因外部扰动、模型偏差、状态误差及控制器响应时间诸多元素,会使得期望路径与MPC 预测路径存在一定误差,对期望路径与预测路径进行拟合,结果如图8 所示。可知随着迭代次数的增加,对应期望路径误差与MPC预测路径误差在迭代次数为15 之后,均逐渐缩减且UAV 预测路径误差≤UAV 期望路径误差,UAV两路径在迭代次数为7 时拟合效果趋于一致,证明预测环航半径收敛于期望环航半径,即在保证完成对运动目标环航的过程中提高路径的预测精度。
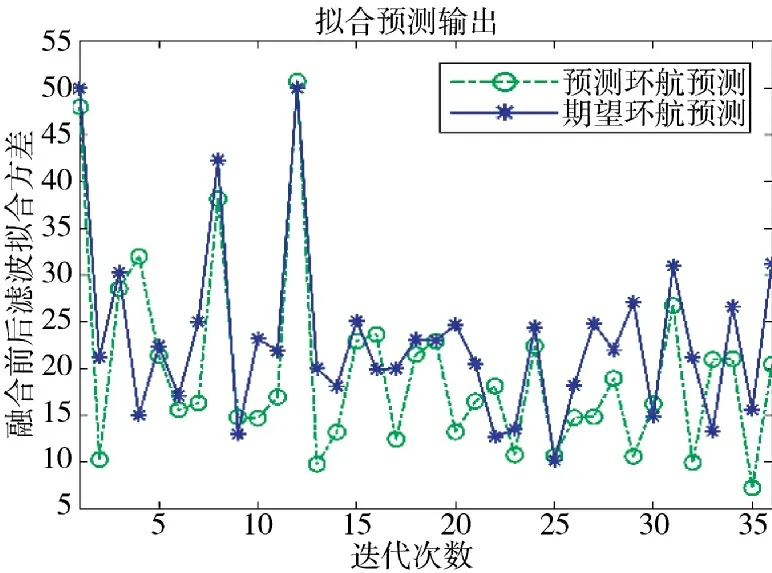
图8 预测环航和期望环航拟合输出Fig.8 Predicted circumnavigation and expected circumnavigation fitting output
在实际UAV 巡航过程中,不仅要保证实际环航半径收敛于期望环航半径,即关于ed 函数极限趋于0。同时考虑到UAV 性能、运动区间范围及PID控制器处理能力,应保证环航航迹的平滑性,即需满足航迹过渡自然且光滑,航向不发生突变[20]。同时还保证了曲线的保凸性,平滑后的航迹经过所有的航点且逼近原始的航迹曲线,通过对该环航数据进行处理,MPC-UIF 融合后平滑性函数输出如图9所示。
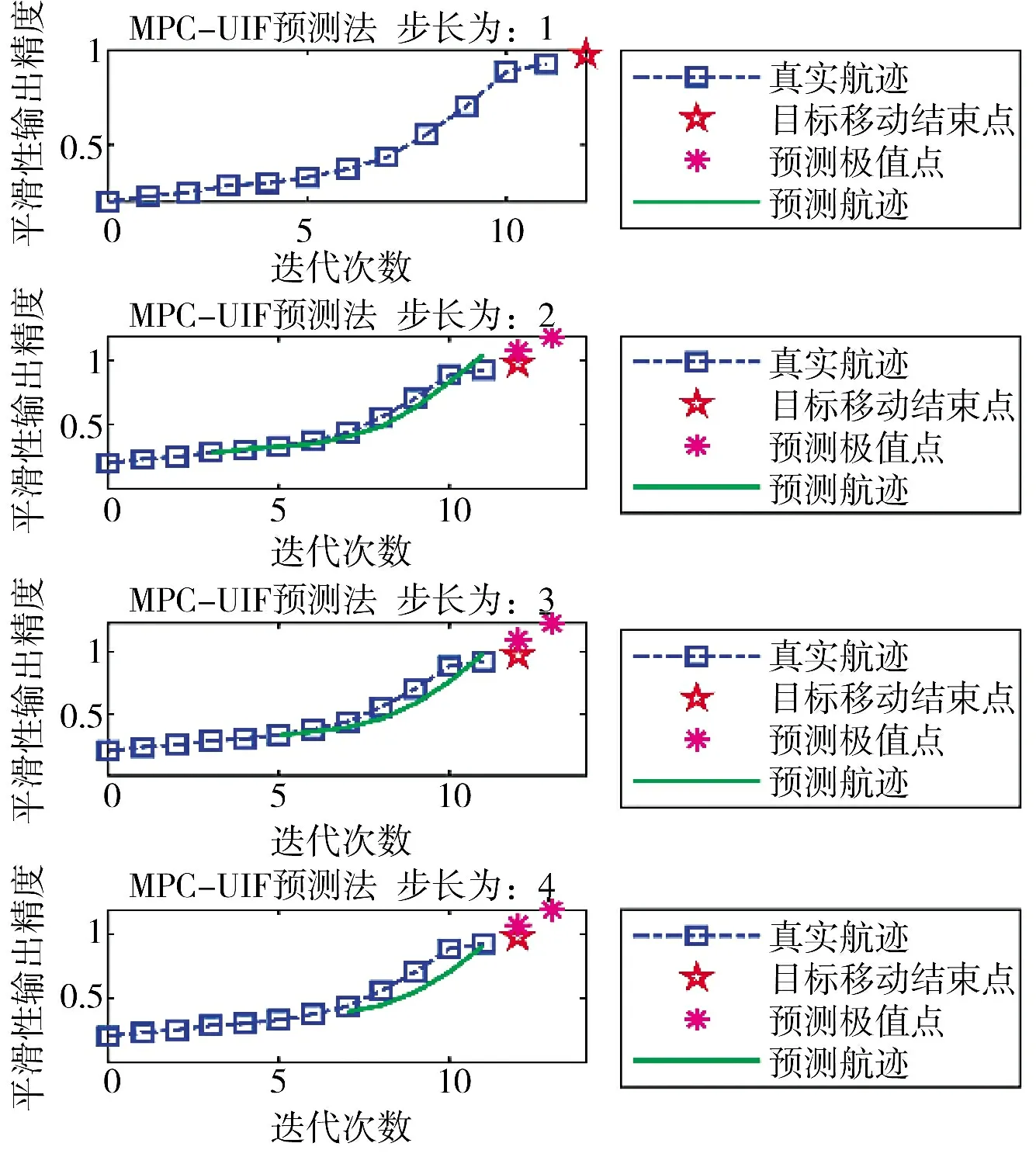
图9 基于MPC-UIF 融合的平滑性研究Fig.9 Smoothness study based on MPC-UIF fusion
通过图9 可知,随着迭代次数的增加UAV 航向趋于平缓,航迹平滑性有所增强,精度得到提高,侧向证明基于融合MPC-UIF 的控制精度和收敛速度得到保证;同时随着步长设定系数的增加,预测航迹会自适应调整以寻求到真实结束点的最短距离。
5 结论
本文针对复杂干扰项下的固定翼UAV 系统,结合自适应MPC 预测和UIF 精度的学习能力,提出具有高性能环航的跟踪控制器。根据所属UAV 性能、全局融合响应设定控制器参数,使得在保证UAV 能够快速收敛于期望半径的同时,提高控制器的精度和速度,较之传统的PID 控制具有更高抗干扰能力和高鲁棒性。未来进一步将深度学习与自监督机制进行耦合控制,来解决反无人机和多UAV自主协同路径规划问题。

