基于时隙和功率分配的联合优化算法*

周绍军，刘晓霞，胡云冰

（1.四川水利职业技术学院信息工程学院，四川 崇州 611231；2.厦门大学信息学院，福建 厦门 361005）

0 引言

随着智能手持设备数量呈指数级增长，5G 核心网络的压力陡增。第三代合作伙伴计划3GPP 提出D2D［1］技术，可有效缓解5G 网络负载，提高本地服务的数据速率。在D2D 模式下，近地设备能够共享蜂窝用户（cellular users，CUs）的资源［2］。然而，这些低功耗设备一般由干电池供电，储能量有限。

无线能量传输（wireless energy transfer，WET）［3］是给低功耗设备补给能量的有效技术。通过WET技术，补充设备能量，延长设备的工作时长。当基站向网络广播了信号，其就会向周围产生电磁波。设备利用能量收集电路，从此电磁波信号获取能量，即完成能量采集（energy harvesting，EH）。因此，蜂窝网络支持（under-laying cellular networks，ULCNs）的EH-使能D2D 通信框架受到广泛关注［4］。

然而，从射频信号采集的能量随时间波动，并呈随机性，而设备的剩余能量影响了资源分配策略。因此，有效地管理EH-使能D2D 通信的ULCNs网络的资源十分重要。依据文献［5］，非正交多址接入（non-orthogonal multiple access，NOMA）是提高频谱效率，资源共享的有效技术。据此，将NOMA 与D2D-ULCNs 相结合，可以有效地提高网络性能。

为此，面向D2D-ULCN 网络，提出基于时隙和功率分配的联合优化算法。主要工作如下：1）建立关于时隙分配和传输功率的能效优化的目标问题；2）考虑到目标问题的非凸性，将目标问题分解两个子问题；再分别利用Dinkelbach 法和连续凸逼近法分别求解；3）通过仿真分析JTAO 算法的性能。性能分析表明，相比于同类算法，JATO 算法通过优化D2D 的发射功率和时隙分配，提升了D2D 群的能效。

1 系统模型

DTX采用NOMA 技术［6］，并配备EH- 供电的电路。将DTX的操作时隙分成两个子时隙。在第1个子时隙内，DTX从基站广播信号中采集能量；在第2 个子时隙，DTX向两个接收设备传输数据。令he和td分别表示DTX的这两个子时隙。

每个CU 占用一个子信道。即子信道数等于蜂窝用户数。每个子信道的带宽为B=W/K，其中，W 表示总的带宽。K 个子信道相互正交。为了简化表述，令ck表示第k 个子信道，其中，k=1，2，…，K。假定所有子信道服从准静态Rayleigh 衰落分布［7］。

图1 系统模型Fig.1 System model

1.1 信道模型

基站向K 个CUs 广播信号。CUs 在时隙T 内通过子信道带宽B 接收信号。DGs 也可占用这些子信道。因此，第k 个CU（Cuk）所接收的信号：

依据式（1），Cuk端的信干比（signal-to-interference-noise ratio，SINR）［8］：

式中，设计的信号是表示属于DRX1端的信号；干扰信号是指DRX1端的信号对DRX1信号的干扰。

DRX1和DRX2端分别利用连续干扰消除（successive interference cancellation，SIC）技术，移除干扰信号，进而提取属于自己的信号。因此，用式（5）和式（6）计算DRX1和DRX2端SINR：

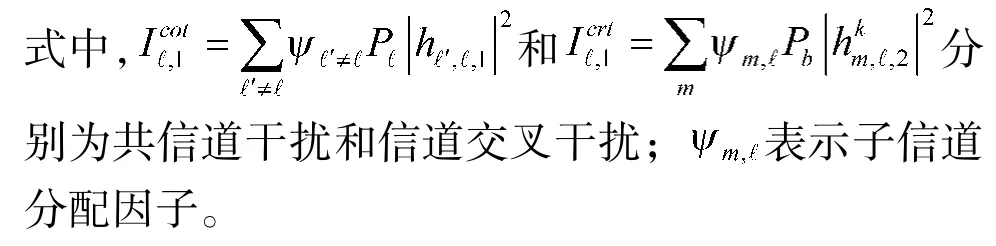
依据文献［10］，DRX1和DRX2端可获取的速率：

1.2 DG 的能效

为了分析网络的能效，需计算基站和DTX端能耗。令Eb表示基站所消耗的能量，其能耗定义如式（10）所示：

式中，Pcb表示基站的静态电路功耗。

在DGs 群中，每个DTX首先从RF 信号采集能量，其在he时隙内所采集能量：

DG 的能效等于总的和速率与总的能耗之比：

2 问题描述

本文旨在通过优化时隙和功率，最大化DGs 的总体能效。为此，联合优化DGs 的时隙分配和发射设备的传输功率以及两个接收设备的功率分配，建立优化能效目标问题P1：

约束项C1确保DTX所消耗的能量不超过其采集的能量；约束项C2确保为非负数，且它们不大于T；约束项C3确保接收端DRX1和DRX2能够成功地执行SIC 操作；约束项C4使DRX1和DRX2能够获取所需的速率；约束项C5对DTX的传输功率进行约束，将其限制于最大传输功率之内；约束项C6使功率分配因子为非负数。

由于目标问题P1 中包含时隙、传输功率以及功率分配因子，目标问题P1 为非凸问题。因此，直接求解P1 问题复杂度很高。为此，将P1 分解成两个子问题，再分而解之，获取次优解。

3 目标问题P1 的求解

3.1 基于Dinkelbach 法求解第1 个子问题

约束项：C3～C6。

由于式（14）仍属非凸问题，采用Dinkelbach法［11］求解，将目标问题P 2 的分数形式转换成相减形式：

约束项：C3～C6。

理论1 的证明过程可查阅文献［12］。Dinkelbach法通过迭代算法求解。

3.2 基于连续凸逼近法求解第2 个子问题

约束项：C3～C6。

首先，利用连续凸逼近（successive convex approximation，SCA）法将凹函数转换成凸函数，形成目标问题P4：

约束项：C3，C5，C6。

因此，等式（25）成立：

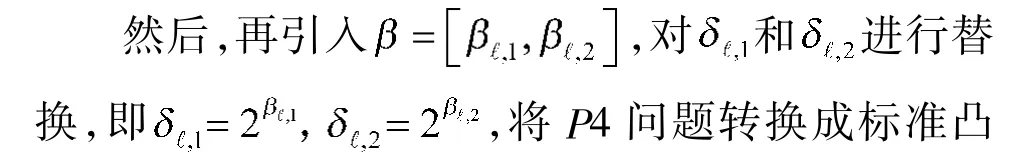
优化问题P5：

由于目标问题P5 属标准凸优化，采用MATLAB 软件提供的CVX 工具求解，获取最优的值，从而优化功率分配因子（）。

4 性能分析

4.1 仿真参数

利用MATLAB 软件建立仿真平台，在半径为400 m 的圆形区域内部署K 个蜂窝用户。由于一个蜂窝用户占用一个子信道，网络内存在K 个子信道。仿真参数如表1 所示。

表1 仿真参数Table 1 Simulation parameters

4.2 参数K 和L 对能效的影响

分析DG 群数对能效的影响，如图2 所示，其中，DG 群数L 从2～20 变化，DG 群半径为30 m。从图可知，能效随L 的增加而下降。原因在于：在L 数越高，子信道之间的共信道干扰越严重，这就降低了能效。此外，能效随K 数增加而上升。这主要是因为：K 值越大，子信道数越多，频谱密度越高，这有利于提升能效。

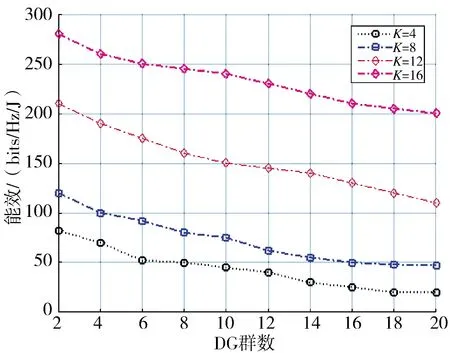
图2 能效随DG 群数的变化情况Fig.2 Change of energy efficiency with the number of DG groups

图3 分析了DG 群半径对能效的影响，其中，DG 群数L 为20。

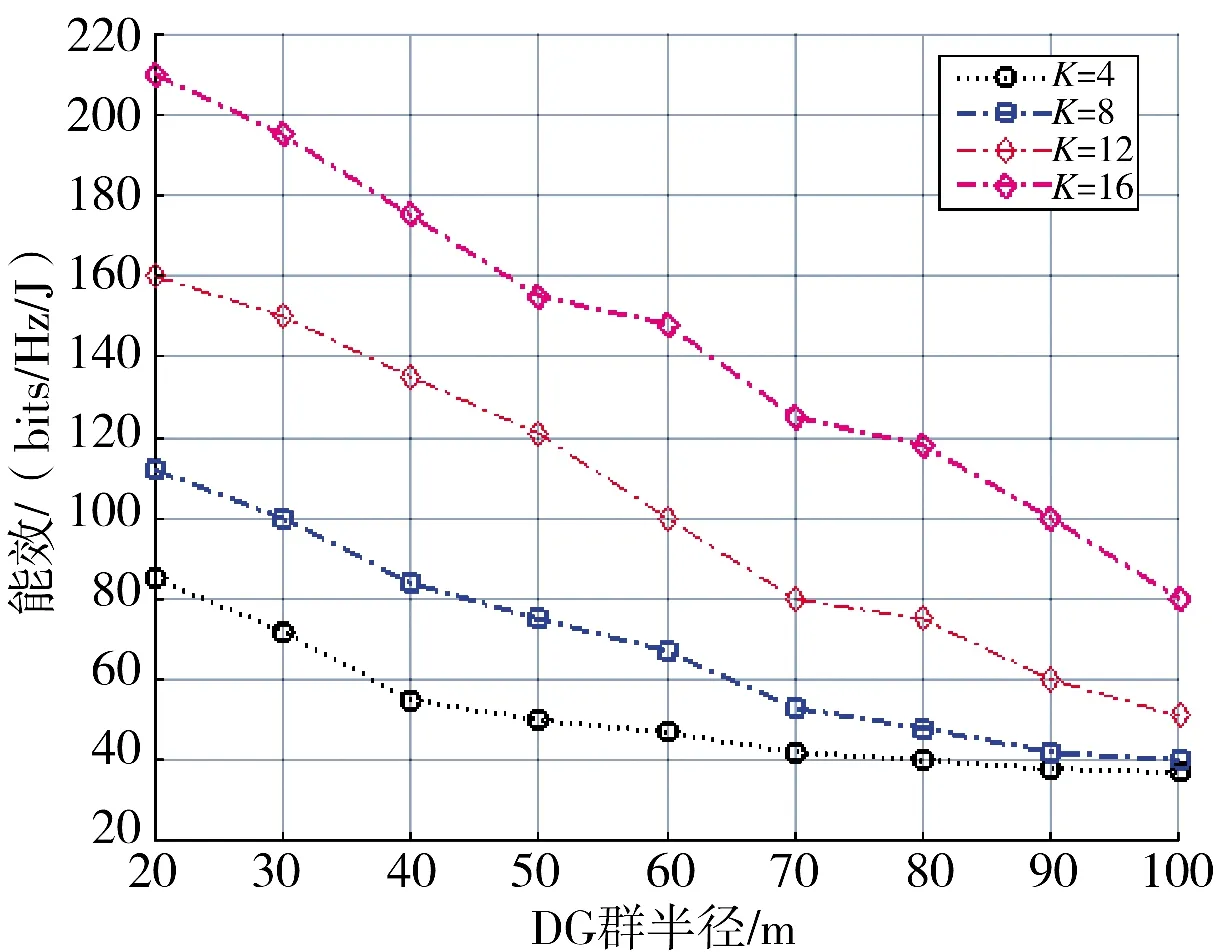
图3 能效随DG 群半径的变化情况Fig.3 Change of energy efficiency with the radius of DG groups

从图可知，DG 群半径越大，能效越低。原因如下：1）当DG 离基站的距离增加，用户就需要增加功率，进而克服路径衰减；2）距离增加使得DT 从BS 接收信号的强度变弱，所采集的能量减少。

此外，观察图3 不难发现，随着DG 群半径的增加，能效下降速率变缓，这归功于NOMA 技术。NOMA 技术给弱信号分配大的功率，阻止了能效随子信道增加而下降。

分析Dinkelbach 法的迭代次数对能效的影响，如图4 所示，其中，DG 群半径为30 m，DG 群数L 为20。从图可知，Dinkelbach 法能够快速地收敛。最初能效较低，但当迭代次数达到4 后，能效能够收敛于一个稳定值。此外，增加CUs 数，并不影响收敛速度。K=6，12，18 只需经过4 次迭代，能效值就收敛。

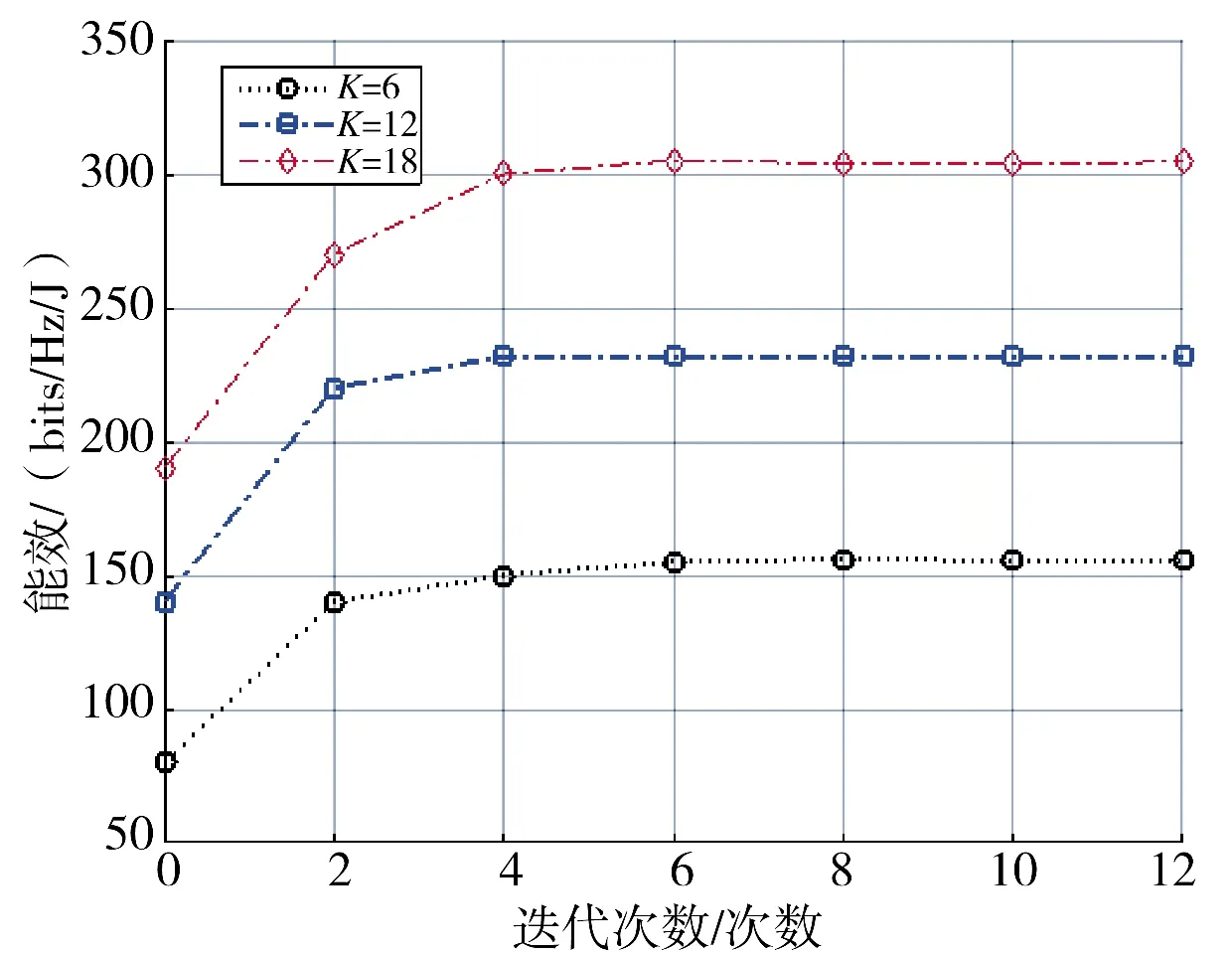
图4 迭代次数对能效的影响Fig.4 Impact of iteration number on energy efficiency

4.3 对比分析

为了更好地分析JTAO 算法在和速率和能效两方面的性能，选择两个同类算法进行参照：1）文献［13］提出联合用户簇群和功率分配和速率提升算法（joint user clustering and power allocation，JUPA）。JUPA 算法采用K-means 算法将用户分成簇群；2）穷举搜索法（Exhaustive Search，EXSE）。EXSE 法是通过搜索目标问题P1 的所有可能解，得到最优解。尽管该算法能够获取全局最优解，但EXSE 法的复杂度高。而JTAO 算法不是直接求解目标问题P1 的全局最优解，而是将其分解两个子问题，再分而求之，得到局部最优解。

图5 显示了D2D 和速率VLtotal随DG 群数的影响，其中，DG 群半径为50 m。从图可知，VLtotal随D2D群数增加而上升，这符合逻辑。依式（9）可知，VLtotal等于各D2D 群速率之和。

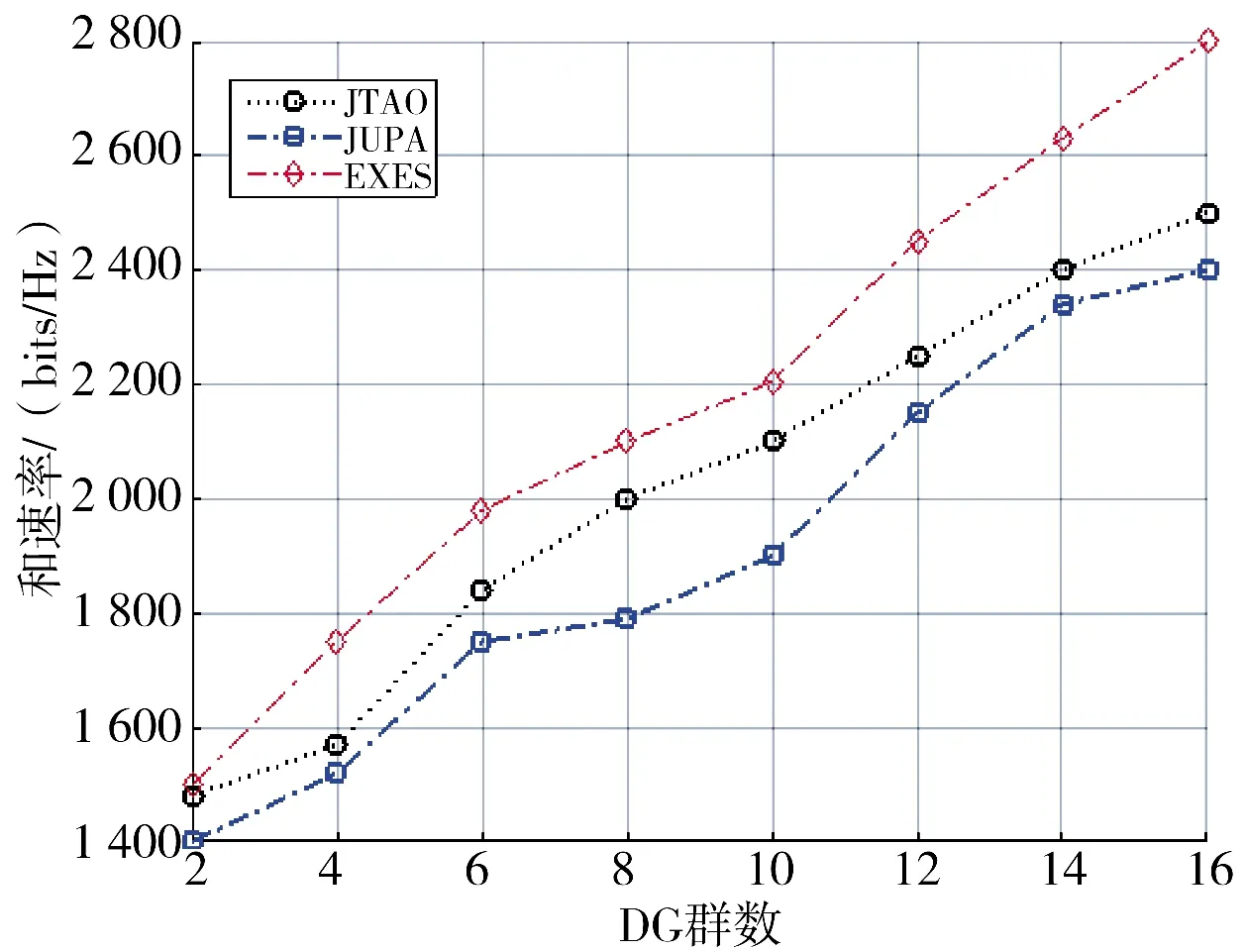
图5 速率随DG 群数的变化情况比较图Fig.5 Comparison of the change of rate with the number of DG groups

相比于JUPA 算法，JTAO 算法提升了和速率。但是JTAO 算法的和速率低于EXSE 法。原因在于：EXSE 法能够获取目标问题P1 的全局最优解，而JTAO 算法获取的是局部最优解。

最后，分析JTAO 算法、JUPA 和EXES 算法的能效，如图6 所示。能效随着DG 群数的增加而缓慢上升。从式（12）可知，DG 群数的增加，提升了和速率，即增大了式（12）的分子；由于DG 群数的增加，也增加了设备能量消耗，即增大了式（12）的分母。由于和速率增加速率更快，能效仍随DG 群数增加而上升。

图6 能效随DG 群数的变化情况Fig.6 Change of energy efficiency with the number of DG groups

此外，相比于EXES 算法，JATO 算法的能效得到提升。从图5 可知，EXES 算法的和速率性能优于JATO 算法。这说明EXES 算法是以高能耗换取高的和速率，最终导致EXES 算法的能效低于JATO 算法。从图6 可知，EXES 算法的能效随DG 群数的增加而缓慢上升。最初，EXES 算法的能效略优于JATO 算法和JUPA 算法，但随着D2D 群数增加，EXES 算法的能效逐渐低于JATO 算法和JUPA 算法。原因在于：DG 群数越多，EXES 算法搜索全局最优解越困难，消耗的能量越多。

5 结论

为了提高支持D2D 蜂窝网络的能效，对D2D发射设备的发射功率和时隙进行优化，形成了基于时隙和功率分配的非凸优化问题。并利用分式规划理论，将非凸优化问题转换成标准的凸优化问题。性能分析表明，通过优化发射功率以及功率分配因子，可提高DG 群的能效。