The integral equation method for the scattering problem of obliquely incident electromagnetic waves in a chiral medium

FENG Lixin,LI Yuan,ZHANG Lei

(1.School of Mathematical Sciences,Heilongjiang University,Harbin 150080,China;2.Mathematics Department,Zhejiang University of Technology,Hangzhou 310014,China)

Abstract：The scattering of an obliquely incident electromagnetic wave by an infinite impedance cylinder which is embedded in a homogeneous chiral medium is considered.Under certain assumptions,the scattering problem can be formulated as a second order elliptic system with generalized oblique derivative boundary conditions for the z components of the electric and magnetic fields.By partly reducing the coupling via a decomposition method and potential theory,the oblique scattering problem is transformed to a system of two integral equations.It is not a usual Fredholm system of the second kind as that in the case of normal incidence,since the system involves the tangential derivatives of the single-layer potential.It is shown that this system of operators is of Fredholm type with index 0.By using the Fredholm theory,the uniqueness and the existence of solutions for the boundary integral equations are justified.A numerical scheme for solving the integral equations is also presented.

Keywords：direct scattering;chiral medium;oblique incidence;uniqueness;existence;integral equation method

0 Introduction

The study of scattering of electromagnetic waves in a chiral medium began two decades ago,a series of relevant works can be found in references [1-14] and the references therein.The obstacle scattering in a homogeneous chiral medium inR3is modeled usually by a boundary value problem for Maxwell’s equations.If the obstacle is an imperfectly conducting cylinder (impedance cylinder) parallel to thez-direction and illuminated by a polarized plane wave at a normal incidence,it is well known that the corresponding electromagnetic scattering can be formulated as a boundary value problem for thezcomponent of either the electric field or the magnetic field,see for instance reference [14].If the incident plane wave obliquely acts on the cylinder,thezcomponents of the electric and magnetic fields cannot be decoupled,and the mathematical formulation becomes more complicated.The scattering problems from the impedance cylinders at an oblique incidence in a non-chiral medium have been studied,see the references [15-29].

In this paper,we assume that the cylinder is embedded in a homogeneous chiral medium and the incident electromagnetic wave acts on this cylinder at an angle not equal to π/2 with respect to the negativezaxis.The study of the situation is much less clear.In reference [12],the direct scattering problem is initially studied,under some simplifications of parameters and a strong condition on the incident angle.In reference [13],the scattering problem is discussed in a more general situation.In the paper,based on the Drude-Born-Fedorov constitutive relations and Maxwell’s equations,we show that thezcomponents of the electric and magnetic fields satisfy a second order elliptic system in the exterior of the cross-sectionDof the cylinder.On the boundary ∂D,we derive a coupledboundary condition with generalized oblique derivatives from the so-called Leontovich impedance boundary condition on the lateral of the cylinder.The unique solvability of the direct scattering problem is proven by using the Lax-Phillips method.The superiority of the Lax-Phillips method is that it allows for proving the complex analyticity of the solution to the direct scattering problem,from which one can prove the uniqueness of the inverse scattering problem.However,the methods used in references [12-13] do not support the numerical computation of the scattering problem directly.In this paper,we investigate the integral equation method to solve the direct scattering problem.By partly reducing the coupling via a decomposition method and potential theory,the oblique scattering problem is transformed to a system of two integral equations.We would like to emphasize that it is not a usual Fredholm system of the second kind as that in the case of normal incidence,since the system involves the tangential derivatives of the single-layer potential.We show that this system of operators is of Fredholm type with index 0.By using the Fredholm theory,the uniqueness and the existence of solutions are justified.Furthermore,we propose a numerical method to solve the integral equations.By this method the far-field pattern of the scattering problem can be computed effectively,which implies the possibility to compute the inverse scattering problem.

The rest of this paper is organized as follows.In Section 1,we give the mathematical formulation of the scattering problem from an impedance cylinder at an oblique incidence in a chiral medium.In Section 2,the existence and uniqueness of the solution to the direct scattering problem are justified by using the Fredholm theory.Section 3 is devoted to a numerical scheme for solving the corresponding integral equations.Finally we give some conclusions in Section 4.

1 Mathematical formulation of the scattering problem

We formulate the scattering of an obliquely incident electromagnetic wave by an infinitely long impedance cylinder which is embedded in a homogeneous chiral medium.Assume that the cylinder is parallel to thezaxis,and its cross-sectionDis of an arbitrary shape withC2boundary ∂D.It is well known that the electromagnetic fields are governed by the Maxwell’s system in the form

divD=0,divB=0

(1)

(2)

together with the Drude-Born-Fedorov constitutive equations for a chiral media

D=(E+β∇×E),B=μ(H+β∇×H)

(3)

whereE,H,DandBare the electric field,the magnetic field,the electric and magnetic displacement vectors inR3,respectively.The parametersandμare assumed to be constants,known as the electric permittivity and magnetic permeability,respectively.Hereβis the chirality admittance withβ≥0,describing the property of the medium to rotate the plane of polarization of electromagnetic waves.Assume that the electromagnetic wave (E,H) is time-harmonic,i.e.the time dependence occurs through a factore-iωt,then we have

∇×E=k2(1-k2β2)-1βE+iωμ(1-k2β2)-1H,divE=0

(4)

∇×H=k2(1-k2β2)-1βH-iω(1-k2β2)-1E,divH=0

(5)

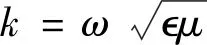
Let

(Ei,Hi)=(ei(x,y),hi(x,y))·e-iωt-iαz

(6)

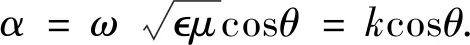
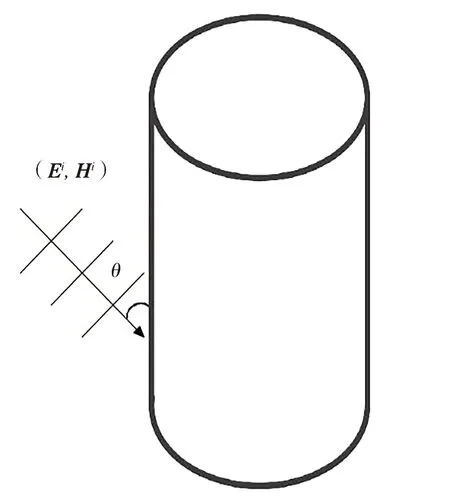
Fig.1 Incident angle θ

(7)

On the lateral of the cylinder,we impose the Leontovich impedance boundary condition

(ν×E)×ν=λ(ν×H)

(8)

whereνis the outward unit normal vector andλis the impedance constant.We assume thatλis positive on ∂D.

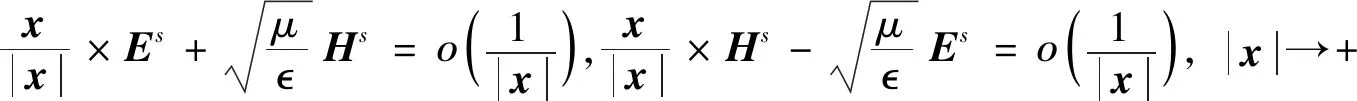
(9)

(10)

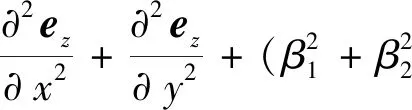
(11)

with the impedance boundary conditions

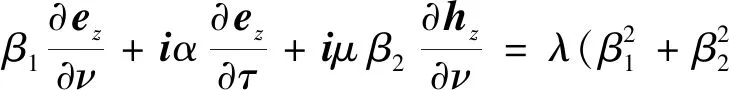
(12)

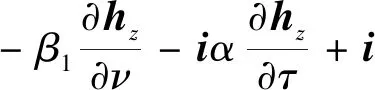
(13)

whereνandτare the unit outward normal and tangent vectors of ∂D,respectively,described in Fig.2.Here the constantsβ1andβ2are determined by

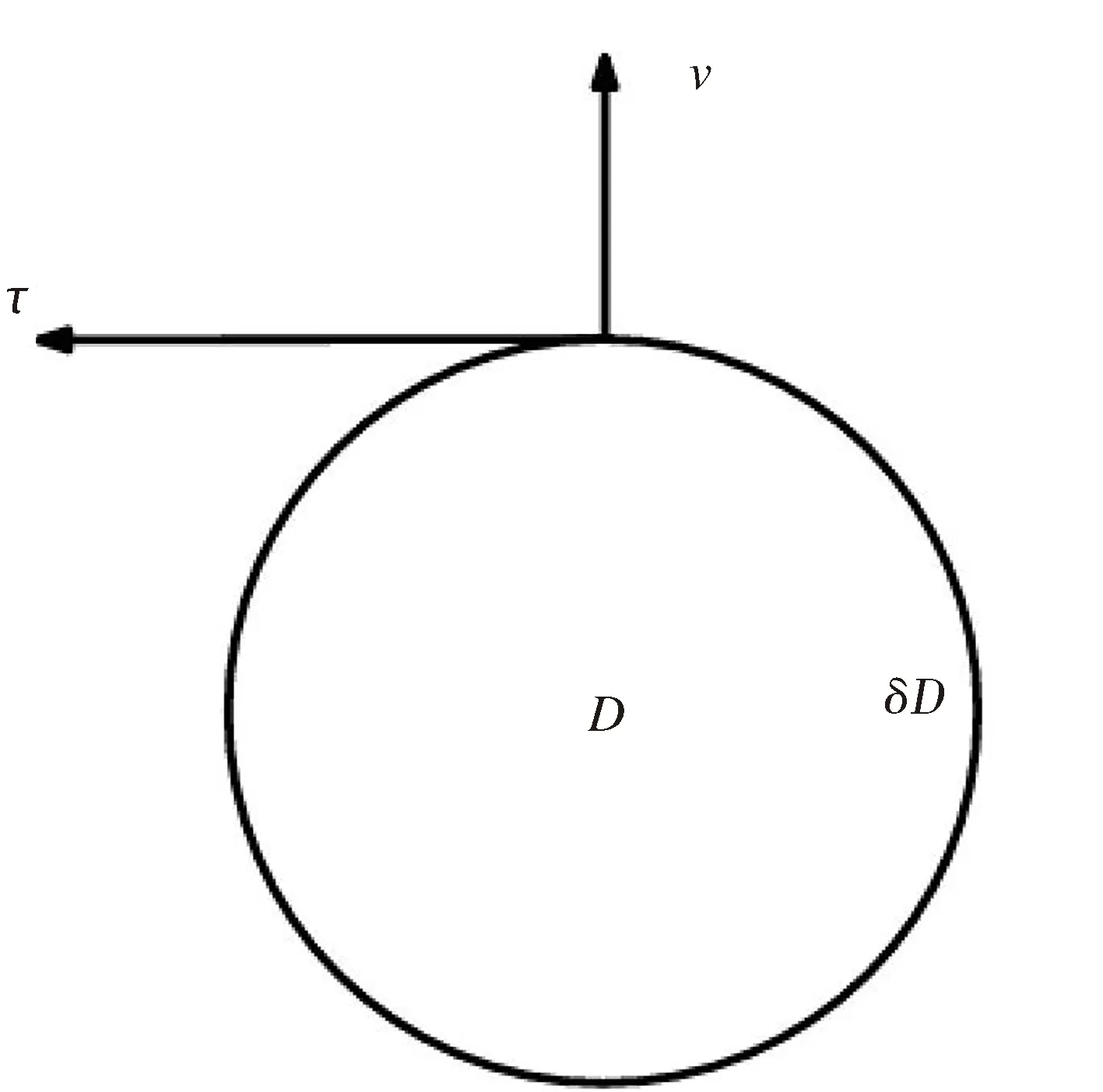
Fig.2 Localized coordinated system

β1=k2(1-k2β2)-1β,β2=ω(1-k2β2)-1

(14)

We note that the equations (10) and (11) are coupled through the lower order terms.To partly reduce this coupling,we introduce the new fieldsuandvby

(15)

Then we can easily derive from (10)～(13) that

(16)

(17)

(18)

(19)

Here,the constants are given by

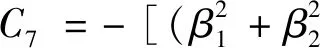
The following relations among the constants are easily derived.

In this paper,we assume thatλ2-μ>0.

We now make the same decompositions for the incident and scattered fields

(20)

(21)

(22)

(23)

wheref1andf2are given by

and

respectively.We also impose the following Sommerfeld radiation condition (S.R.C.) for (us,vs)：

(24)

wherer=|(x,y)|.

2 Analysis of the direct scattering problem

In this section,we start with the following uniqueness result：

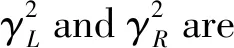
For the detailed proof process of this conclusion,please refer to a previous paper published by us (see the reference [13]).

Now,we prove the existence of the solution to the systems (20)～(24) by using the integral equation method.To this end,we define the fundamental solution to the Helmholtz equation in2with wave numberkj,j=L,Rby

We further define the operators

where

Some properties of these operators are given as follows,which play a key role in the proof of our main result in this section.

Lemma1Let ∂Dbe of classC2,α.Then the operatorsSj,K′j：L2(∂D)→L2(∂D)are compact,andH′j：L2(∂D)→L2(∂D)is bounded.

Lemma2The operatorsH′0andK′0have the relation：

(K′0)2-(H′0)2=I

whereIis the identity operator.

The proofs of Lemma 1 and Lemma 2 are referred to reference [28].We are now in a position to state the main result of this section.

ProofWe seek the solutions (20)～(24) in the form of single layer potential

(25)

(26)

with unknown densitiesφ1,φ2∈L2(∂D).Using the standard jump relations of single-layer potential,we derive from systems (22) and (23) that

(27)

(28)

LetAbe the operator defined by

Then in terms of

the systems (27)～(28) become

Aφ=f

(29)

where the superscriptTdenotes the transposition.

Now we proceed to prove the solvability of system (29) in two steps.In the first step,we show thatAis a Fredholm operator with index 0.To this end,we decomposeAas

A=-B+Q

(30)

with

and

Since the kernels ofH′jandH′0have the same singularity,the operators

H′j-H′0：L2(∂D)→L2(∂D),j=L,R

are compact,and hence,

Q：L2(∂D)×L2(∂D)→L2(∂D)×L2(∂D)

is compact.

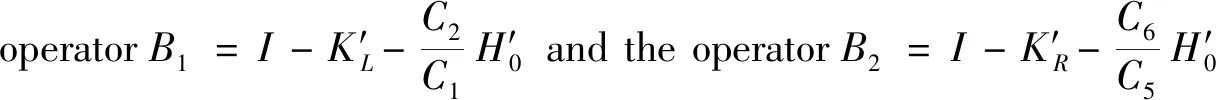
We define the operatorBi(t)(i=1,2)with a parametert∈[0,1]by

We now show thatBi(t) is also Fredholm with index 0 for anyt∈[0,1].DecomposeBi(t) as

B1(t)=B11(t)-K′L,B2(t)=B22(t)-K′R

with

Define the operator

Obviously,Li(i=1,2)is bounded fromL2(∂D)→L2(∂D).Using Lemma 2,we derive that

L1B11(t)=B11(t)L1

Similarly,

This means thatLiis a two-sided regularizer ofBii(i=1,2).It follows from Theorem 2.24 in reference [21] thatBii(t) is a Fredholm operator.Note thatK′LandK′Rare compact inL2(∂D),we have that the operatorsBi(i=1,2) are also Fredholm.

On the other hand,since the operatorH′0is bounded,Bi(t),i=1,2 are continuous with respect tot.Hence,we have

Ind(Bi(1))=Ind(Bi(0))=0,i=1,2

which implies fromBi=Bi(1)that the operatorsBi,i=1,2are of Fredholm type with index 0.FurthermoreBis Fredholm type with index 0.It follows from system (29) thatAis also Fredholm operator with Ind(A)=Ind(B)=0.

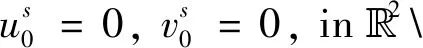
(31)

and have

(32)

Using the jump relation of single-layer potential,we have

(33)

where the indices “+”and “- ”denote the standard limits from2Donto the boundary ∂D,respectively.Combing systems (31),(32) and (33) yields

The proof is complete.

3 Numerical scheme for solving the integral system

The numerical discretization of the boundary integral equations (27)～(28) is based on the Nyström method in reference [30].For the readers’ convenience,we outline here the treatment of the associated integral kernels and the quadrature rules used.Assume that the closed curve ∂Dis smooth enough,and has the parametrization

with2π-periodic functionsx(t),y(t).We define

for a given densityψandX=X(t)∈∂D.By direct calculations,we have the parametric expressions ofK′,SandH′：

with the kernel functions

wherep(t)=(x′(t),y′(t))=|X′(t)|·τ(X(t)),n(t)=(y′(t),-x′(t))=|X′(t)|·ν(X(t)).

In terms of the singularities of kernels,we decompose the functionsK(t,r),S(t,r)andH(t,r) as follows：

whereJ0andJ1are the Bessel functions of order zero and order one,respectively.The kernelsK2,S2andH2are defined by

with diagonal terms

whereris the Euler’s constant.

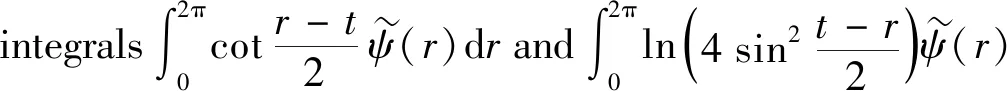
with the weights

Other regular integrals involved in systems (27)～(28) possess periodic smooth kernels,and hence they can be approximated by simple rectangular rule.

In the second step,we want to check the efficiency of the proposed method.To this end,we focus on a special case where the scattered wavesusandvsare expressed exactly byΦL(·,Z1)and ΦR(·,Z2).HereZ1andZ2are two points insideD,and then define two boundary functions by

and

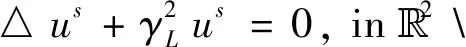
(34)

(35)

(36)

(37)

(38)

According to the asymptotic behavior of the Hankel function,the far-filed patterns ofusandvscan be expressed as

(39)

(40)

On the other hand,we obtain from systems (25)～(26) that the far-field patterns ofusandvscan be expressed in the forms

(41)

and

(42)

LetDbe a kite-shaped domain with the boundary expression

x(t)=2cost+1.3cos2t-1.3,y(t)=2.5sint,t∈[0,2π]

The geometric shape is described in Fig.3.In the following,Z1=(0.2,0.2)andZ2=(-0.3,-0.3)are two points insideD,and we set the constants=1,μ=1,ω=π,θ=π/2and the chirality admittanceβ=0.1.The boundary impedance is taken asλ=2.

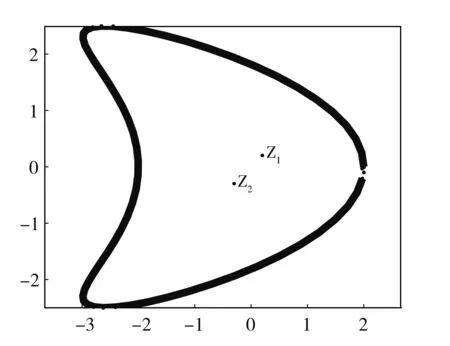
Fig.3 Geometry of D,z1 and z2 are two points inside D

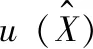
Table 1 Exact solutions of for different incident angle t

In numerical implementations,we choose the equidistant collocation points by setting

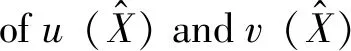
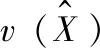
Table 2 Exact solutions of for different incident angle t

4 Conclusions

In this paper,we study the scattering of electromagnetic wave by an imperfectly conducting infinite cylinder embedded in a homogeneous chiral medium at oblique incidence.The oblique scattering problem is modeled as a boundary value problem for thezcomponents of electric field and magnetic field.Based on potential theory,our oblique scattering problem in a homogeneous chiral medium is transformed to a system of two integral equations.It is not a usual Fredholm system of the second kind as that in the case of normal incidence,since the system involves the tangential derivatives of the single-layer potential.We show that this system of operators is of Fredholm type with index 0.By using the Fredholm theory,the uniqueness and the existence of solutions are justified.A numerical scheme for solving the integral equations is also presented.We emphasize that our results are quite general in the sense that ifα=0 orβ=0,our models reduce to the well-known cases of scattering in a normal incidence or in a usual homogeneous medium,respectively.In addition,the numerical implementation of the scheme presented here is considered also.