基于认知诊断的两阶段试题推荐方法

李强 王彬彬 陈磊 冯辉

摘要：针对个性化试题推荐系统中，未标注知识点试题的推荐精度欠佳问题，提出了一种基于认知诊断的两阶段试题推荐方法。第一阶段由专家筛选出学习单元中的典型试题并进行知识点标注，运用认知诊断模型，量化得出学生的知识掌握状态。第二阶段基于学生的知识掌握状态，计算学生之间的知识含盖关系，并基于含盖关系对未标注试题进行个性化推荐。实验表明，文章提出的试题推荐方法，推荐试题的平均作答正确率达到了90%，平均试题超纲率低于10%，显著优于现有的基于kNN和矩阵分解的协同过滤推荐方法。

关键词： 试题推荐; 认知诊断; DINA; 试题标注; 认知状态

中图分类号：TP391.3      文献标识码：A

文章编号：1009-3044（2023）13-0025-04

开放科学（资源服务）标识码（OSID）

0 引言

随着互联网发展，在线教育获得了大规模的普及[1-4]。线上学习与答题成为学生自我检测、自我提升的主要途径之一[1，5-9]。依据学生的学习进度和知识掌握状态，进行精准的个性化试题推送，可以有效地帮助学生巩固知识，深度思考。经过数年的积累，现已产生了海量试题资源[10]，这些试题资源又关联了数以万计的知识点[11]，传统的通过人工选题的方式，不仅费时费力，而且很难依据学生的学习进度和知识掌握状态进行个性化推荐。

近年来，不少学者将认知诊断模型和推荐系统应用到学生的个性化试题推荐中[4-9]，取得了不错的推荐效果。但是在模型应用时，需要人工对海量的试题数据提前进行知识点标注，这一标注过程费时费力，且对于新的未标注的试题无法有效推荐。针对以上问题，本文提出了一种新的方法，该方法首先基于少量的标注试题估计出学生的认知状态，然后依据学生的认知状态找到存在知识含盖关系的学生，之后找出这些学生在历史未标注试题上的答题数据，过滤出回答正确率高的试题，进而向学生进行个性化试题推荐。通过本文提出的方法，可以有效地降低人工标注成本，提升未标注试题的推荐精度和效率。

1 两阶段试题推荐算法

基于认知诊断模型的个性化试题推荐算法包含两个阶段。第一阶段，由教师选出典型试题，并进行知识点标注，依据学生在典型试题上的答题结果，运用认知诊断模型估计出学生量化的知识掌握状态。第二阶段依据学生的知识掌握状态找到相似的学生，依据相似学生的历史答题数据（答题时间、答题结果等），进行个性化试题推荐。

1.1 认知状态估计

认知诊断模型旨在量化学生的认知状态，近年来获得了广泛的应用。其中DINA认知诊断模型，因其简洁性和可解释性成为学者们研究的热点[12-15]。DINA认知诊断模型基于学生的答题结果和试题知识点关联矩阵进行建模，通过EM、MCMC等方法进行参数估计，进而获得学生量化的认知状态和试题参数信息。在DINA模型中，用离散的二分向量来表示学生认知状态，如[αi=[1，0，1，1，0]]表示学生[i]在五个知识点上的掌握状态，其中1表示学生掌握了对应的知识点，反之，0表示学生未掌握对应的知识点。在运用DINA认知诊断模型前，需要提前获知学生在试题上的答题结果以及试题与知识点的关联关系。通常用矩阵[X]来表示[N]个学生在[M]道試题上的答题结果，矩阵中的元素[xi，j]表示学生[i]在试题[j]的答题结果，如果[xi，j=1]表示学生[i]答对了试题[j]，反之，[xi，j=0]表示学生回答错误。用矩阵[Q]来表示[M]道试题与[K]个知识的关联关系，矩阵中的元素[qj，k]表试题[j]与知识点[k]的关联关系，[qj，k=1]表示答对试题[j]需要掌握知识点[k]，反之[qj，k=0]表示试题[j]与知识点[k]无关。DINA模型的目标是最小化预测答题结果与真实答题结果之间的误差，来估计出学生量化的认知状态[α]。理想情况下，预测的答题结果[zi，j]计算方式如下：

[zi，j=k=1Kαi，kqj，k] （1）

其中[zi，j]表示理想情况下学生[i]能否答对试题[j]，[αi，k]表示学生[i]是否掌握了知识点[k]，[qj，k]表示试题[j]是否涉及知识点[k]。DINA模型中还引入了试题失误率[s]和试题猜对率[g]来模拟真实答题场景。引入试题失误率和猜对率后，学生[i]在试题[j]上的答对概率[pi，j]可以表示为：

[pi，j=1-sjzi，jgj1-zi，j] （2）

得出答对概率[pi，j]后，便可以依据目标函数对学生的认知状态进行估计了。

[α=minα，s，gFP，X] （3）

由DINA模型的定义可以看出，在认知诊断前，需要先标注出试题与知识点的关联关系。然而当前试题资源已非常庞大，标注过程需要耗费大量的人力物力，普通的教育组织和机构很难完成这项工作，而且新的试题仍然在逐年递增，因此很难实时全面地对试题数据进行标注。

针对这一问题，本文提出了一种基于部分试题的认知诊断方法。首先针对每个学习单元，由专家抽取出少量典型试题，然后通过人工方式对典型试题进行知识点标注，之后进行完备度测量，确保这些试题能够均匀覆盖学习单元中涉及的全部知识点。

经过认知诊断模型评估，得出学生量化的认知状态后，便可以依据学生的认知状态进行后续的试题推荐了。

1.2 个性化试题推荐

针对现有推荐系统在未标注试题上的推荐精度欠佳问题，本文提出了一种基于学生知识含盖关系的试题推荐方法。若学生[u]掌握了学生[v]所掌握的所有知识点，则称学生[u]在认知状态含盖学生[v]，用[cu，v=1]来表示。比如学生[u]的认知状态为[αu=1，1，1，1，0]，学生[v]的认知状态为[αv=1，1，1，0，0]，其中学生[u]掌握了前四个知识点，而学生[v]只掌握了前三个知识点，此时学生[u]掌握了学生[v]所掌握的所有知识点，因此[cu，v=1]，即学生[u]在认知状态上含盖学生[v]。注意含盖关系是不可逆的，[cu，v=1]并不代表[cv，u=1]，但如果两个学生的认知状态完全相同，则这两名学生在认知状态上互相含盖。针对有含盖关系的学生，学生间的含盖度计算方法可以表示为：

[ru，v=k=1Kαu，k-αv，k] （4）

其中[ru，v]表示学生[u]对学生[v]的认知含盖度，显然[ru，v]越大代表学生[u]相对于学生[v]掌握的知识点越多。针对没有含盖关系的学生，令其含盖度为[-1]。依据两两学生的认知含盖度便可以得出含盖度矩阵[R]。

[R=r1，1…r1，N???rN，1…rN，N]      （5）

矩阵[R]的第[u]行代表学生[u]对其他学生的认知含盖度，比如[ru，*=[1，2，0，-1，…]]表示学生[u]相对于前三个学生的认知含盖度分别为1、2、0，即学生[u]在认知状态上含盖前三个学生，同时比这三个学生分别多掌握了一个、两个和零个知识点。但对于第四个学生，学生[u]对其认知含盖度为-1，代表学生[u]在认知状态上并不含盖学生四。

矩阵[R]的第[v]列代表其他学生对学生[v]的含盖度。比如[r*，v=[2，0，1，-1，…]]表示前三个学生在认知状态上含盖了学生[v]，且分别比学生[v]多掌握了两个、零个和一个知识点。第四个学生对学生[v]的认知含盖度为-1，表示第四个学生在认知状态上并不含盖学生[v]。

在进行试题推荐时，需要确保推荐试题关联的知识点学生均已掌握。因此针对学生[u]，需要遍历含盖度矩阵[R]的第[u]行，并找到[ru，*≥0]的学生，并按含盖度从小到大对找到的学生进行排序，找出这些学生答对率较高的试题，去重后依次进行推荐。试题推荐的详细流程如算法1所示。

[算法1：个性化试题推荐算法 输入：待推荐试题的学生编号[u]，待推荐的试题数量[c]，所有学生答题记录[X]，认知含盖矩阵[R]

输出：为学生[u]推荐的试题列表 1. 初始化学生[u]认知含盖的学生列表stus

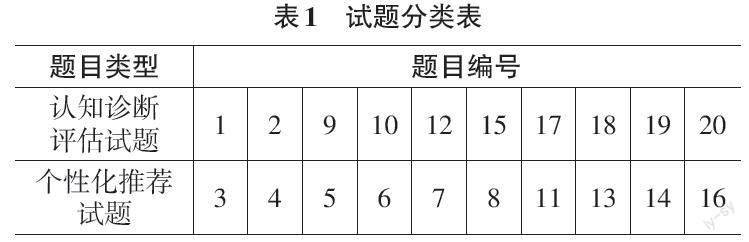
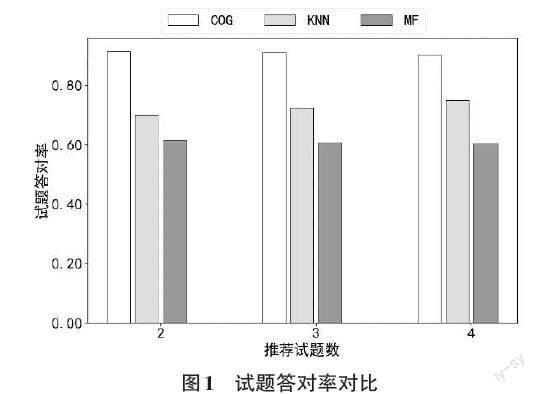
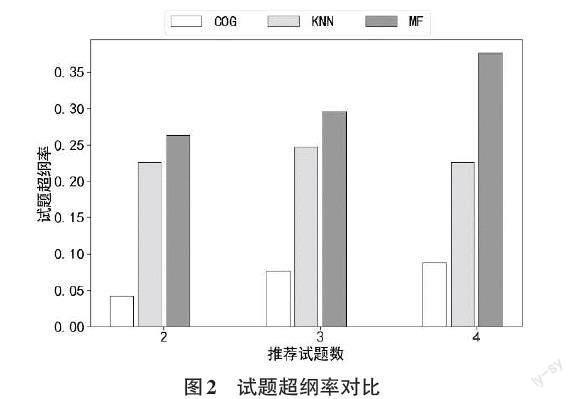
2. For i=0; i

3.   If [ru，i≥0] and [i ≠u]：

4.     stus.append（[i]）

5.   End If

6. End For

7. stus = sort（stus）

8. questions = [X[stus]]

9. correct = mean（questions）

10. rec_qus_idxs = argsort（correct）[：：-1]

11. return rec_qus_idxs[：c] ]

算法1包含四个输入，分别是待推荐试题的学生编号[u]，待推荐的试题数量[c]，学生答题记录[X]和认知含盖矩阵[R]。其中[X]为去除已标注试题外的所有学生答题历史记录。

算法输出为学生[u]推荐的试题列表。

算法的第1行为初始化学生[u]认知含盖的学生列表，第2到第6行为寻找学生[u]认知含盖的学生，并将学生加入学生列表中。第7行为通过认知含盖度从小到大对学生列表进行排序。第8行为依据排好序的学生列表获取其对应的历史答题记录。第9行为计算答题记录中各题的平均正确率。第10行为对正确率从大到小进行排序（逆序），并获取排序后的试题编号。第11行获取正确率最高的指定数量试题，并返回给系统进行推荐。

通过以上算法，可以依据学生在典型试题上评估出的认知状态，对未标注的试题数据进行个性化试题推荐，从而达到推荐时既可以考量学生学习进度和知识状态，又可以减少试题标注工作量的效果。

2 实验与分析

2.1 实验数据

实验采用的数据集为广泛使用的分数减法数据集[15-20]。该数据集包含536名学生在20道试题上的真实答题数据，试题共涉及8个知识点，已由专家提前完成标注。

实验中将试题数据分成两部分，其中10题用于认知状态评估，另外10题用于个性化推荐。表1给出了两类试题的索引编号。

2.2 评价指标

为了衡量本文提出的方法是否有助于巩固学生所需知识，加深学生的理解，本文采用學生在推荐试题上的作答正确率来验证方法的可行性。同时为了防止推荐试题涉及的知识点超出了学生掌握范围，本文还会计算试题超纲率来衡量推荐试题的质量。

假定给学生推荐的试题集合为[Φ={φ1，φ2，...，φN}]，[φi]表示为学生[i]推荐的试题集合。则作答正确率的计算方法如式（6）所示：

[precision=i=1Nj∈φiXi，ji=1Nφi ] （6）

其中[j∈φiXi，j]表示学生[i]在推荐试题中答对的题数，[φi]表示给学生[i]推荐的题目数。显然[precision]的值越大，代表推荐的试题作答正确率越高，越有助于学生进行知识巩固和提升。

试题超纲率是指超出学生认知范围的推荐试题占比。试题中涉及的知识点超出学生的掌握范围，则认为试题超纲，用指示函数[I（i，j）]来表示试题是否超纲。

[Ii，j=1     ，k=1Kqj，k1-αi，k>00，     k=1Kqj，k1-αi，k=0] （7）

上式中[qj，k1-αi，k=1]，则表示试题中包含了学生未掌握的知识点。

依据指示函数[I（i，j）]便可以计算出推荐试题的超纲率。

[ext=i=1Nj∈φiIi，ji=1Nφi ] （8）

其中[j∈φiIi，j]表示推荐给学生[i]，但超出学生[i]知识范围的试题数。显然[ext]值越小，表示超纲的试题越少，推荐的试题质量越高。

2.3 算法对比

为了验证本文提出的方法相对于传统方法的推荐效果，本文将与基于kNN和基于矩阵分解的协同过滤方法进行对比。

kNN协同过滤方法依据答题结果计算学生之间的相似性，找到k个最相似的学生，过滤出这些学生答对的试题，从而完成个性化试题推荐。

矩阵分解协同过滤方法通过对学生答题结果进行矩阵分解，得出学生特征和试题特征，依据学生特征计算学生相似性，找出相似学生答对的试题，并进行互相推荐。

2.4 结果分析

图1给出了三种推荐方法在作答正确率指标上的对比结果。其中橫坐标为向每个学生推荐的最大试题数，纵坐标为所有学生平均作答正确率。可以看出本文提出的推荐方法（COG），无论向学生推荐2题、3题还是4题，推荐试题的作答正确率均在90%以上。

图2给出了三种推荐方法在试题超纲率指标上的对比结果。其中横坐标为向每个学生推荐的最大试题数，纵坐标为推荐试题中超纲试题的占比。可以看出本文提出的推荐方法（COG） 在试题超纲率上均低于10%。

3 结束语

基于学生学习进度和知识掌握状态进行个性化试题推荐，可以有效地提升学生的学习效率。针对海量的未标注试题推荐精度欠佳的问题，本文提出了基于认知诊断的两阶段试题推荐方法。既可以基于学生现有的知识水平，又可以有效地解决未标注试题的推荐效率问题。基于公开数据集的实验表明，本文提出的方法推荐试题的平均答对率超过了90%，试题超纲率低于10%，验证了方法的有效性。

参考文献：

[1] 陈恩红，刘淇，王士进，等.面向智能教育的自适应学习关键技术与应用[J].智能系统学报，2021，16（5）：885-898.

[2] 中国互联网络信息中心.第50次中国互联网络发展状况统计报告[EB/OL]. https：//www.xdyanbao.com/doc/b9npm6ky5s？bd_vid=12305363540120140075.

[3] 管佳，李奇涛.中国在线教育发展现状、趋势及经验借鉴[J].中国电化教育，2014（8）：62-66.

[4] Wang F，Liu Q，Chen E H，et al.Neural cognitive diagnosis for intelligent education systems[J].Proceedings of the AAAI Conference on Artificial Intelligence，2020，34（4）：6153-6161.

[5] 齐斌，邹红霞，王宇，等.基于协同过滤和认知诊断的试题推荐方法[J].计算机科学，2019，46（11）：235-240.

[6] Zhuang Y，Liu Q，Huang Z Y，et al.A robust computerized adaptive testing approach in educational question retrieval[C]//Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval.July 11 - 15，2022，Madrid，Spain.New York：ACM，2022：416-426.

[7] 熊慧君，宋一凡，张鹏，等.基于深度自编码器和二次协同过滤的个性化试题推荐方法[J].计算机科学，2019，46（S11）：172-177.

[8] Zhuang Y，Liu Q，Huang Z Y，et al.Fully adaptive framework：neural computerized adaptive testing for online education[J].Proceedings of the AAAI Conference on Artificial Intelligence，2022，36（4）：4734-4742.

[9] 朱天宇，黄振亚，陈恩红，等.基于认知诊断的个性化试题推荐方法[J].计算机学报，2017，40（1）：176-191.

[10] 刘铁园，陈威，常亮，等.基于深度学习的知识追踪研究进展[J].计算机研究与发展，2022，59（1）：81-104.

[11] 崔炜，薛镇.松鼠AI智适应学习系统[J].机器人产业，2019（4）：84-94.

[12] Tong S W，Liu J Y，Hong Y T，et al.Incremental cognitive diagnosis for intelligent education[C]//Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining.August 14 - 18，2022，Washington DC，USA.New York：ACM，2022：1760-1770.

[13] 汪文义，郑娟娟，宋丽红，等.认知诊断模型参数估计算法比较[J].江西师范大学学报（自然科学版），2022，46（3）：291-299.

[14] Ma W C，Torre J.An empirical Q-matrix validation method for the sequential generalizedDINA model[J].British Journal of Mathematical and Statistical Psychology，2020，73（1）：142-163.

[15] 王超，刘淇，陈恩红，等.面向大规模认知诊断的DINA模型快速计算方法研究[J].电子学报，2018，46（5）：1047-1055.

[16] Culpepper S A.Estimating the cognitive diagnosis（＼varvec{Q}＼） matrix with expert knowledge：application to the fraction-subtraction dataset[J].Psychometrika，2019，84（2）：333-357.

[17] DeCarlo L T.On the analysis of fraction subtraction data：the DINA model，classification，latent class sizes，and the Q-matrix[J].Applied Psychological Measurement，2011，35（1）：8-26.

[18] de la Torre J，Douglas J A.Model evaluation and multiple strategies in cognitive diagnosis：an analysis of fraction subtraction data[J].Psychometrika，2008，73（4）：595-624.

[19] Terzi R，Sen S.A nondiagnostic assessment for diagnostic purposes：q-matrix validation and item-based model fit evaluation for the TIMSS 2011 assessment[J].SAGE Open，2019，9（1）：2158 24401983268.

[20] 汪文义，宋丽红，丁树良，等.非参数认知诊断方法下诊断结果的概率化表征[J].心理科学，2021，44（5）：1249-1258.

【通联编辑：李雅琪】