基于高阶累积量的多径信道调制方式自动识别

蒋俐瑞琪 石皓文

摘要：在多径信道条件下，信道衰落和接收机滤波器失配会导致信号调制方式识别效果变差。针对这种情况，研究分析了有效的信号调制方式识别方法。基于高阶累积量结合盲信道估计的算法实现了多径信道环境下调制信号的自动识别。并改进了特征参数和决策方法，使不同调制方式的特征参数之间的距离更大。使用K-NN近邻法进行识别，在低信噪比条件下识别效率提高。仿真结果表明，改进算法能有效地抑制多径衰落。

关键词：多径衰减 ；高阶累积量；信道估计；调制方式识别；K-NN

中图分类号：TN911        文献标识码：A

文章编号：1009-3044（2023）13-0019-03

开放科学（资源服务）标識码（OSID）

0 引言

现代通信技术的高速发展使得通信信号的调制方式日趋多样化、复杂化。在复杂的通信环境和严重的噪声干扰条件下，通信信号调制方式的准确分类识别面临越来越严峻的挑战。

当前，信号调制识别方法可分为两类：基于决策理论的似然比识别方法（Likelatio-basi，LB）和基于特征提取的模式识别方法（Feature-basi，FB）。基于LB的辨识方法是以假设检验理论为基础，以贝叶斯最小误差概率实现最优解，但仍然存在实际应用中理论推导复杂和计算量大的问题。基于FB的调制方式识别方法是通过提取信号调制方式特征，并与理论特征的结果进行比较，完成识别，具有复杂度低、所需先验信息少、效率高和对各种模型匹配度好的优点。特征提取方法包括以下主要方法：信号瞬时特征、谱相关特征、小波变换特征、高阶累积量（Higher Order Cumulant，HOC） 特征等。

多径信道干扰会造成接收信号严重的符号间干扰。受到符号间干扰的影响，信号的幅度和相位都会发生变化，从而导致调制识别效果不佳。过去，高斯信道下的调制识别算法没有考虑这些影响。因此，研究多径条件下的调制识别算法具有重要的应用价值。

近年来，HOC已广泛应用于调制方法的自动识别。文献[1]采用主成分分析法白化噪声，并基于快速独立分量分析法分离混合信号，使信号转变为相互间最大的独立分量，最后通过计算HOC判定各信号的调制方式。该方法对2PSK、4PSK和16QAM信号进行调制分类，达到一定的识别效果。为了降低多径信道对信号调制识别的影响，文献[2]中将自适应调制识别应用于多径衰落信道场景下，基于贝叶斯序贯推理法充分挖掘和利用信道隐含的动态相关特性，并实现调制方式和信道增益的联合估计。文献[3]提出了通过四阶和六阶HOC进行多进制数字相位调制和正交幅度调制的识别方法，分类器采用支持向量机（Support Vector Machine，SVM）。文献[4]利用信号的四阶、六阶、八阶累积量构造多个特征参数，实现对2ASK、2FSK、BPSK、QPSK、16QAM和OFDM 6种常用数字信号调制方式的识别。文献[5]基于典型调制信号的数学模型分析了信号的频域和统计域特征，并基于信号的HOC和平方谱提取了4个特征参数，提出了一种基于特征提取的直接分类识别方法用于复合调制信号的识别，并总结了具体的识别过程。在信噪比为2 dB条件下，8种调制信号的识别率达到98%。多径信道传输条件下BPSK、QPSK、16QAM和64QAM的分类和识别一直是一个难题。文献[6]提出信道估计后使用四阶HOC识别BPSK，QPSK，4QAM，16QAM和64QAM这4种信号。文献[7]构造了5个特征参数，基于分类决策树，通过设置合理阈值来识别8个常用的通信信号。

1 特征参数提取

采样后，通信信号从模拟信号转换为数字信号，数学描述如下：

[y（n）=k=0L-1h（k）x（n-k）+g（n）]         （1）

式中[x（n）]为要传输信息序列，调制样式未知。[h（k）]，[k=0，1，...，L-1]是信道的衰减系数，信道长度为[L]。[g（n）]是均值为0，方差[σ2g]为高斯白噪声。

当今，通信环境越来越复杂，无线传输、移动通信等通信环境中存在着大量的反射体和散射体，所以信道中多径效应明显。由于信号或信道模型不匹配等问题，过去常规调制识别算法的识别效能会下降，无法达到所需的识别性能。

本文研究HOC作为特征参数在多径信道中的信道估计和调制识别的应用。选择了四种不同的HOC作为特征参数。下面各式中随机变量[x]对应传输信息[x（n）]。

[C40（x）=cum{x，x，x，x}=M40（x）-3M220（x）]   （2）

[C41（x）=cum{x，x，x，x*} =M41（x） -3M20（x）M21（x）]         （3）

[C42（x）=cum{x，x，x*，x*} =M42（x） - |M20（x）|2-2M]       （4）

[C63x=cum{x，x，x，x*，x*，x*}=M63-6M41M21+18M220+12M321]   （5）

信号通过信道传输的过程可以看作是信号与信道的单位冲激响应[h（n）]的卷积过程。如果信号[xn]在多径信道传输之后接收到的信号为[y（n）]，则[y（n）=x（n）*h（n）]。

结合式（1-5） 和HOC的特性，可以得出如下结论：

[C63（y）=cum（y，y，y，y*，y*，y*）=C63（x）k=0L-1|h（k）|6]  （6）

[C40（y）=cum{y，y，y，y}=C40（x）k=0L-1h4（x）]   （7）

[C41（y）=cum{y，y，y，y*}=C41（x）k=0L-1h3（x）h*（k）] （8）

[C42（y）=cum{y，y，y*，y*}=C42（x）k=0L-1|h（x）|4] （9）

[C21（y）=cum{y，y*}=C21（x）k=0L-1|h（x）|2+σ2g]    （10）

在多径衰减信道的条件下，由于接收信号受到信道的影响，接收信号的HOC不能直接作为发送信号的HOC进行调制识别。

如果能从接收信号中估计出多径信道的传输特性，就可以计算发射信号的HOC。

2 盲信道估计

信道估计是根据接收到的信号数据估计信道模型的参数的过程。如果信道是线性的，信道估计就是估计系统的单位冲激响应。

定义[x（n）]的四阶混合矩：

[M40，x（τ1，τ2，τ3）=E{x（n）x（n+τ1）x（n+τ2）x（n+τ3）}=M40，x，τ1=τ2=τ3=00，其他] （11）

[y（n）]的四阶混合矩：

[M40，y（τ1，τ2，τ3）=E{y（n）y（n+τ1）y（n+τ2）y（n+τ3）}]  （12）

结合上式和公式（1） 可以得到：

[M40，y（τ1，τ2，τ3）=M40，xk=0L-1h（k）h（k+τ1）h（k+τ2）h（k+τ3）] （13）

令[τ1=τ2=L-1，τ3=k，k=0，1， ... ，L-1]，得到[M40，y（L-1，L-1，k）]的值：

[M40，y（L-1，L-1，k）=M40，xh（0）h（L-1）h（L-1）h（k）]当[k=0]时，得到：

[M40，y（L-1，L-1，0）=M40，xh（0）h（L-1）h（L-1）h（0）]信道的估计量：

[h（k）=h（k）h（0）=M40，yh（0）h（L-1）h（L-1）h（k）M40，yh（0）h（L-1）h（L-1）h（0）] （14）

在实际过程中，信号的混合矩和HOC是从样本的均值中得到的，因此，可以从样本均值估计信道系数：

[h（k）=n=1Ny（n）y（n+L-1）y（n+L-1）y（n+k）n=1N[y（n）y（n+L-1）]2] （15）

式中[k=0，1， ... ，L-1]。

通过得到的信道的估计量，可以推导得到样本信号的HOC：

[C40（x）=C40（y）k=0L-1h（k）4]         （16）

[C41（x）=C41（y）k=0L-1h（k）3h（k）*]      （17）

[C42（x）=C42（y）k=0L-1|h（k）|4]        （18）

[C63（x）=C63（y）k=0L-1|h（k）|6]          （19）

[C21（x）=C21（y）-σ2gk=0L-1|h（k）|2]      （20）

由前面的分析可知，正确估计多径信道的参数进行后，可以由受多径干扰的接收信号计算出原信号对应的识别参数，进一步完成调制识别。

3 K-NN分类识别

调制分类识别是通过选择适当的决策准则和分类器来识别被测信号[8]。K-NN近邻算法设计简单，训练时间短、识别效率高。其主要设计思想是：首先找出距离新样本最近的K个训练样本，再采取“少数服从多数”的策略，判断此样本的所属类别。

对于待识别的N个属于类[（ω1，...，ωN）]的样本，定义函数[F]是关于样本[x]和固定模板[Ts]的函数。

[gd（x）=F（di（x，TS））]         （21）

式中，[di（x，Ts）]是未知样本[x]和固定模板[Ts]之间的距离。

分类准则：如果[gi（x）=mingd（x）]，[i=1，2，...，N]，则未知样本[x]属于类[ωi]。

定义分类函数为未知样本到特征值的欧式距离，即：

[gd（x）=|X-μi|]

式中[X]是未知样本的特征参数[（F1，F2）]，[μi]是已知调制方式的训练样本的特征值。

4 识别流程

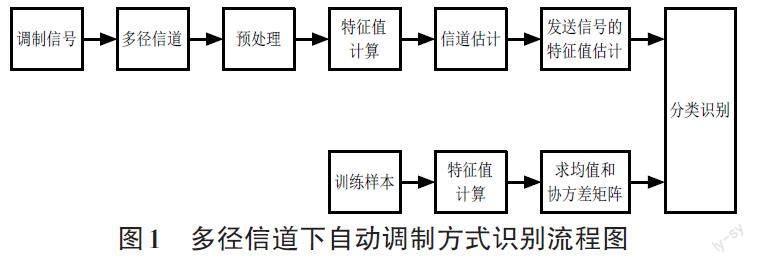
识别的具体流程如图1所示。首先，需要对接收到的信号进行特征提取；然后进行盲信道估计，去除多径信道传输对特征值的影响；估计出发送信号的特征值，送到分类判决器；同时训练样本为已知调制方式的信号，对其进行特征值提取，计算不同调制方式特征值的均值和它们之间的协方差矩阵，将均值和协方差矩阵送到分类器中；最后，根据决策规则、分类器确定接收信号的调制模式，以实现调制方式识别的目的。

5 仿真结果与对比

本文的调制识别系统主要识别BPSK，QPSK，16QAM和64QAM。仿真条件为：载波频率[fc=20.4MHz]，符号率[fd=6MHz]，采样率[fs=64MHz]，噪声为高斯噪声，信噪比为｛-10，-5，0，5，10，15｝dB。每种调制信号在不同信噪比下产生20个样本，则每种调制信号会产生120个样本，用作训练样本。在相同的仿真条件下，每种调制信号在不同信噪比下生成100个样本，则每种调制信号会生成600个样本。这些样本用作测试数据，以测试系统的识别率。

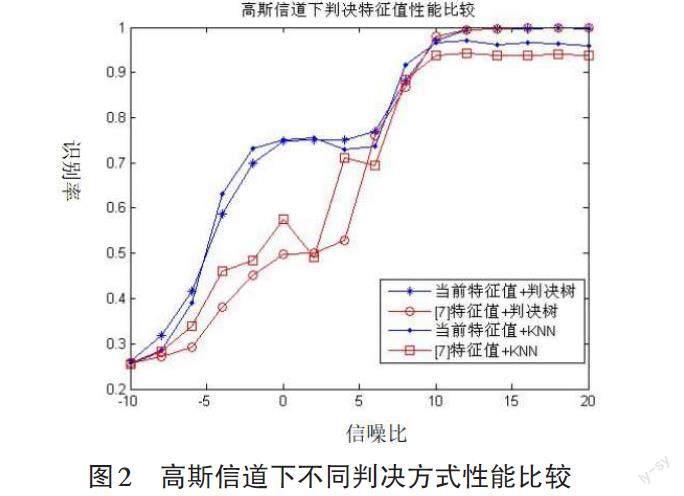
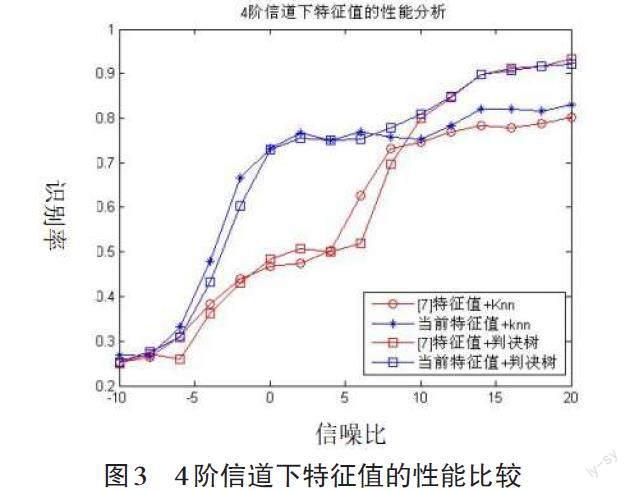
从图中可以看出，本文提出的方法在低信噪比下具有更好的性能。在多径衰减信道下，尤其是信道阶数比较大的条件下，利用本文提出的特征值结合K-NN近邻算法作为判决准则，能在低信噪比下达到較高的识别率。这是因为K-NN通过计算样本与训练样本组之间的距离来分类。判决树是通过特征值的大小直接划分，在低信噪比的情况下错误概率大。

6 结论

由于多径信道的干扰，传统的调制识别算法效果不理想，甚至无效。本文采用HOC来识别BPSK、QPSK、16QAM和64QAM这几种数字调制信号。在未知信号调制方式的情况下，采用四阶和六阶HOC的组合作为特征参数，实现信道估计和信号调制的准确识别。

本文提出的特征值，在高斯信道和多径衰减信道下都能够提高系统的识别性能，是一种有效的改进。K-NN近邻算法能在低信噪比条件下更好地判断样本的调制类型。

参考文献：

[1] 袁莉芬，宁暑光，何怡刚，等.基于高阶累积量特征学习的调制识别方法[J].系统工程与电子技术，2019，41（9）：2122-2131.

[2] 付俊强，李蓉，赵成林，等.基于贝叶斯序贯推理的自适应调制识别算法[J].系统工程与电子技术，2015，37（12）：2860-2864.

[3] Pei-hua LI.Modulation recognition of communication signals based on high order cumulants and support vector machine[J].The Journal of China Universities of Posts and Telecommunications，2012（19）：61-65.

[4] 田偉光，李华圣，沈振惠，等.基于高阶累积量的数字调制信号检测与识别方法[J].中国无线电，2022（2）：56-58.

[5] 许琦敏，万峻，何羚，等.基于高阶累积量和信号平方谱特征的复合调制信号盲识别[J].电子学报，2022，50（2）：426-431.

[6] Wu H C，Saquib M，Yun Z F.Novel automatic modulation classification using cumulant features for communications via multipath channels[J].IEEE Transactions on Wireless Communications，2008，7（8）：3098-3105.

[7] 李跃，郭兴吉，赵欣.基于高阶累积量的调制方式识别研究[J].西南科技大学学报，2018，33（3）：64-68.

[8] 杨欣，谢小娟，杨喜，等.基于多特征判定的定频通信信号快速检测研究[J].电脑知识与技术，2022，18（16）：36-39.

【通联编辑：唐一东】