滚动轴承寿命预测的相似性匹配优化方法研究

崔玲丽 金瓯 王鑫

摘要： 传统相似性寿命预测方法忽视退化过程的局部演变特性，导致预测精度较低；传统时、频域等特征指标难以实现早期故障监测，且退化后期局部波动较大。引入高斯函数趋势拟合策略，提出改进的相似性匹配优化方法。提出基于高斯混合模型的 Jensen‐Renyi 散度健康指标，准确跟踪滚动轴承退化演变趋势。由于实际全生命周期退化信号难以大量获取，因此构建双指数函数模型，模拟退化信号，并验证仿真数据扩充参考字典集的有效性。采用高斯函数拟合退化数据并提出参数相似性原则，实现剩余使用寿命预测。滚动轴承全生命周期退化实验数据分析结果验证了所提方法可以有效提高剩余寿命预测精度。

关键词： 故障诊断；滚动轴承；剩余寿命预测；双指数函数；参数相似性

中图分类号： TH165+.3；TH133.33+2 文献标志码： A 文章编号： 1004-4523（2023）03-0854-07

DOI：10.16385/j.cnki.issn.1004-4523.2023.03.028

引 言

滚动轴承是重大高端装备中应用最广泛和最关键的基础部件之一，其发生故障导致装备不能正常工作甚至停机会造成极大的经济损失和安全隐患。因此，实时监测轴承工作状态是故障与健康管理的关键环节。目前故障与健康管理包括两个方面：故障 诊 断 与 剩 余 使 用 寿 命（Remaining Useful Life，RUL）预测。大多数故障诊断方法仅在故障已经产生时做出诊断结论，如果能够尽早检测故障，甚至能够预测故障的发生及剩余使用寿命，在实际中具有更重要的意义。因此预测方法的相关研究得到了较多关注。

寿命预测往往需要大量全生命周期数据，全生命周期定义为轴承运行初始时间至退化特征大于安全阈值的首个时间点。但此类信号在实际中不容易获取，因此通过数字仿真技术进行扩充是一种解决手段。Idriss 等［1］基于轴承全生命周期的磨损变化与摩擦力变化趋势，提出动态磨损演变模型。该模型可以有效模拟旋转机械运转中的动态冲击，并利用多种力学模型综合估计磨损演化阶段之间的过渡点，对比演化模型与实验模型，验证了其有效性。Cui 等［2］将轴承退化过程分为稳定阶段、缺陷萌生阶段、缺陷传播和损伤扩展阶段，考虑到时变形貌和刚度的耦合激励，建立了综合的动态模型来模拟缺陷扩展。但是这些模型计算量较大，难以快速推广至不同型号轴承的预测中。Zhang 等［3］根据振动响应信号的频率分量取决于故障类型和运行条件，振幅与退化程度有关等机理建立了轴承退化仿真模型，除振动响应外的其他部分均被视为噪声。但是退化部分幅值依靠单指数函数，退化形式单一。Wang等［4］基于正态随机变量构建随机退化点集，确立健康阶段与退化阶段的转折点后，通过设定双正态分布的均值与方差构造函数，基于递推的思想求解函数期望最大化时的参数值。但是，此种方法需要依赖专家经验。本文旨在通过故障脉冲与幅值调制技术构建数字孪生仿真信号，这种方式运算量较小，且符合轴承运行过程中的实际情况，同时能保证故障信号退化趋势的多样性。

获取轴承振动信号后，从轴承中挖掘退化信息受到国内外学者的广泛关注，主要包含时域、频域、时频域等多域特征提取。均方根值（RootMeanSquare，RMS）是机械RUL预测中使用最广泛的健康指标（HealthIndicator，HI）。此外有学者从小波系数中提取RMS和峰值，以预测轴承的RUL。Ga？perin 等［5］从包络谱中提取齿轮啮合频率的功率密度，以预测齿轮的 RUL。Medjaher 等［6］計算在不同时间段捕获的两个系列振动信号之间的相关系数作为HI。Ocak等［7］使用隐马尔可夫模型（HiddenMarkovModel，HMM）融合多个特征，并计算HMM 在健康阶段的概率作为轴承的 HI。但是这些方法存在对早期缺陷不敏感及随着退化严重程度的增加而剧烈波动等不足。为克服这些局限性，本文提出一种基于高斯混合模型和 Jensen‐Renyi 散度的特征提取算法，该算法在轴承状态前期较为敏感，后期 不 会 产 生 较 大 的 随 机 扰 动 干 扰 对 剩 余 寿 命 的计算。机械的 RUL 定义为“从当前时刻到使用寿命结束的时间长度”，对于 RUL 的计算有多种方法，相似性方法为寿命预测领域中数据驱动类方法。You［8‐9］引入扩展的权函数，建立鲁棒性评价框架对权函数进行评估，改进了寿命的不确定性评估方法。Liu等［10］通过使用匹配矩阵的相似性度量来比较任意两个退化过程的特征，从而能够获得较高的长期预测精度，但是提取匹配矩阵的过程十分复杂，难以完成滚动窗口的多次重复计算。Liu 等［11］利用了历史样本和现场测试样本之间的内在关系并计算了内在差异，以进行更准确的性能退化预测。该方法可以充分利用有限的历史数据集，但是通过多次循环使用同 一 样 本 ，会 导 致 在 预 测 中 产 生 线 性 误 差 。 You等［12］针对相似性寿命预测权函数进行了研究，分析调整参数取值对预测精度的影响。但是使用的权函数仍然无法解决退化特征局部波动带来的预测误差。Gu 等［13］提出了新的权函数计算方法，增加状态值变量使得权函数对不同工况有更好的适应性。但是对单独工况下轴承振动数据的相似性度量效果较差。相似性度量往往采用欧式距离判定，欧式距离无法对向量中的每个具体元素单独考虑，导致随机波动对相似性带来很大误差。综上所述，本文提出一种相似性匹配优化方法用于滚动轴承剩余寿命预测。相似性匹配优化算法采用拟合函数消除数据随机波动，通过数学推导研究参数对函数趋势的影响，得出相似性度量的计算公式，最终实现滚动轴承的剩余使用寿命预测。

1 算法理论

在寿命预测中，因为轴承原始振动信号无法直观表征退化趋势，首先需要提取轴承信号退化特征。其次，由于相似性方法为数据驱动方法，预测精度依赖于样本数量。而轴承全生命周期实验信号难以获取，为解决小样本数据带来的问题，需要通过仿真信号构建字典集并验证其有效性。最终查询字典集得到测试轴承的剩余使用寿命。

1. 1 轴承退化特征提取

由于轴承振动信号中包含退化信息、啮合冲击、噪声等，因此许多传统健康指标存在随机波动较大的情况。

针对振动信号随机扰动会对趋势分析造成影响，本文拟采用高斯混合模型（GaussianMixtureModel，GMM）与简森‐雷尼散度（Jensen‐RenyiDi‐vergence， JRD）结合对轴承数据进行预处理。GMM 是一种参数模型，可以用来描述从轴承振动信号中提取的多维特征向量的概率分布。给定由N个观测值组成的d维特征集X =（ x1，x2，…，xN ），GMM 由以下方程定义：

因此，一个完整的 GMM 是由均值 μi，协方差 σi 和混合权重wi组成的，即λ=（wi，μi，σi）。上述公式中GMM的似然函数最大化得到的参数τ是使用期望最大化（ExpectationMaximization，EM）算法求解的。

需要注意的是，在计算公式（3）之前需要预先定义混合组分的数量，为此，规定贝叶斯信息准则的公式为：式中 m 为估计参数数。

GMM 模型混合组分的最佳数量将是提供最低BIC 值的重要因素。

基于概率分布可以进一步求解散度。Renyi 熵是 Shannon 熵的一个扩展，具体如下所示：式中 w1，w2，…，wn为对应概率分布（ProbabilityDistribution，PD）的权重。利用JRD的数学特性，可以提取轴承的健康指标。当估计了轴承全生命周期对应的PDs 后，再计算 JRD，就可以评估退化程度。当轴承保持健康状态时，JRD 测量值将近于零，一旦轴承发生早期退化 JRD 测量值就会增加。轴承健康指标提取步骤如下：

（1）提取轴承各类传统时域、频域健康指标；

（2）利用从轴承健康状态下的信号样本中提取的特征向量对 GMM 模型进行训练，根据式（4）计算出的最小 BIC 值，选择最优 GMM；

（3）将测试特征向量提供给最优 GMM 模型，利用公式（1）～（3）计算相应 GMM 分量的后验概率；

（4）利用公式（6）对测试特征向量相关的 GMM‐PDs 进行 JRD 的计算。

1. 2 相似性方法

相似性方法为数据驱动方法，具体步骤为建立字典集，基于测试数据查询字典集。

1. 2. 1 建立字典集

本文提出通过构建仿真信号建立字典集。轴承全生命轨迹信号分为两部分：健康部分、退化部分。其中健康状态下的轴承信号主要为环境噪声，没有冲击信号。轴承在故障阶段往往会伴随着故障冲击，随着使用寿命的增长，故障沖击随之变大。冲击的形式是以故障频率为基础的周期性脉冲，脉冲的幅值在一定区间内随机波动。

轴承脉冲响应信号可表示为：式中 I 为脉冲数；J 为系统模态数；Aij 为第 i 个脉冲时第 j 个系统频率的幅值，具体大小为［0，0.5］中的随机值；T 为脉冲的理论周期；τi 为理论周期与实际脉冲时间的差值；εj 为不同模态下对应的阻尼比；fdj为不同模态下对应的系统频率。

仿真过程中，一些关键参数设置如下：转速为2000 r/min，轴承故障频率为 236.4 Hz，模态频率分量为 2000，4000 Hz；不同模态下阻尼比为 0.1，0.05；采样率为 3 kHz；每次采样长度为 1 s。

脉冲仿真信号如图 1 所示。

退化仿真信号由三部分组成：振动响应信号、环境噪声、系统噪声。环境噪声是机械设备安装场所的固有噪声干扰，不会产生很大的变化。系统噪声是一种振动干扰，它可能来自于设备内部，并随着轴承损坏程度的加重而增加。因为轴承在退化过程中呈现非线性状态，所以在仿真信号构建中采用双指数函数模拟退化趋势。

轴承全寿命仿真信号可表示为：

f（t）=（a1eb1+a2eb2）x（t）+η1（t）+λη2（t）（8）式中 a1，a 2 为反映振动幅值变化的参数；b1，b 2 为反映轴承退化速率的参数；η 1 与 η 2 分别为环境噪声和系统噪声，以轴承健康状态为参照，环境噪声与系统噪声的信噪比设置-25 dB；λ 反映系统噪声随损坏程度增加而增加的速率。

健康状态仿真信号主要为信噪比较小的高斯白噪声。数学特征表现为噪声的均值与均方根值较小。将健康状态与退化状态的模拟信号组合起来，即构建了轴承全寿命信号。具体仿真结果如图 2所示。

将轴承全寿命周期信号进行特征提取并求解退化起始点，得到轴承退化曲线构建的字典集。退化起始点的求解可以有效降低字典集向量的长度与寿命预测的计算量，并且减少轴承健康状态对寿命预测的干扰。

1. 2. 2 查询字典集

传统相似性预测方法是截取当前时间点之前的测试数据，与字典集中退化样本数据进行比较，通过欧式距离的计算确定数据之间的相似性，欧式距离与相似性程度成反比。欧式距离计算公式如下：式中 a，b 分别为截取测试数据与样本数据的向量。向量作差并求向量二范数，在空间意义上为两个向量之间的距离，也称为距离范数。但是传统相似性方法存在局限性，在相似性度量的向量中元素权重相同，每个元素对相似性判定提供等价的影响。在实际寿命预测过程中，由于时间点越接近当前时刻的元素对趋势性分析的关键性越高，因此本文提出基于高斯拟合与参数匹配的改进相似性预测方法。

首先对测试数据与样本数据进行数据预处理：

式（10）为高斯函数，对数据有着高精度的拟合作用，通过高斯函数拟合的方式将向量变成函数表达式。高斯函数中有 3 个参数分别对函数起到不同的作用，b1 控制函数位置，a1和c 1 控制函数趋势，通过构建参数向量，引入参数相似性，求解出参数向量的欧式距离。拟合函数之间的相似性在坐标系上体现 为 积 分 运 算 。 假 设 实 验 信 号 拟 合 参 数 为（ a1，b1，c 1 ），样本信号拟合参数为 （ a 2，b 2，c2 ），在数学坐标系下衡量函数之间距离，可以采用积分求解。取任意长度区间对两个函数模型求解积分，即可获得对相似性的度量；由于传统相似性度量为向量二范数，这种度量方式基于数据遍历法计算，前期波动对退化趋势判定产生较大影响。优化方法则降低了计算过程中轴承数据局部波动带来的相似性度量误差。

S 为相似性度量结果，以下为推导结果：

上述结果直接反映出测试数据与样本数据退化趋势的相似性。最后给各个样本的相似性赋予权重，对寿命进行加权求和得出最终的预测寿命。

1. 3 方法流程

针对传统相似性方法中相似性度量忽略信号时效性及预测精度低的问题，本文提出了一种基于高斯拟合与参数相似性改进的相似性方法。首先，利用 GMM 与 JRD 提取退化特征；然后，通过双指数函数构建仿真信号；最后，利用高斯函数进行退化信号拟合提取形状参数，计算参数相似性预测寿命。

改进相似性寿命预测具体算法如下：

（1）构造仿真信号字典集。通过构建指数衰减型脉冲信号并通过双指数函数进行幅值调制，最后叠加上噪声。

（2）通过GMM计算轴承信号的概率密度分布，然后基于分布结果计算 JRD。

（3）计算轴承全生命周期信号的退化起始点，提取其退化部分，建立查询字典集。

（4）将测试信号与字典集内退化信号进行高斯拟合，查询字典，利用公式（12）求解相似性。

（5）基于相似性赋予对应权重，并与样本信号真实剩余寿命加权求和，计算测试轴承剩余使用寿命。

具体算法流程图如图 3 所示。

2 仿真分析

基于双指数函数对轴承全生命周期信号进行仿真，通过对形状参数设置区间内的随机波动，模拟轴承不同退化速率的趋势。图 4 为部分仿真信号的振动波形图。

获得轴承仿真振动信号后，进行特征提取，得到轴承仿真信号退化趋势，如图 5 所示。由图 5 可知，健康状态转变为退化状态时，健康指标 HI 会发生突变 ，呈剧烈上升趋势。采用阈值报警技术（AlarmBound Technique， ABT）区 分 两 种 状 态 ，即 确 定TSP（Time to Start Prediction）点。对选定窗口内的数据进行一次回归拟合，以拟合曲线所估计的窗口首尾两点健康指标的比值为预警值，判断其是否超过预设的警戒线。如果未超过则认为没有检测到轴承退化痕迹，若超过则认为轴承已经开始退化。

轴承退化起始点计算数据如表 1 所示。

截取信号退化起始点后的部分构建样本字典，结果如下：

构造未退化至失效阈值的测试数据，将测试数据与字典集数据进行高斯函数拟合获取参数向量，并基于当前监测时间点逐一查询字典，基于公式（12）计算相似性大小，賦予字典内样本不同的权重，并将权重归一化处理。最终，将字典数据剩余寿命加权求和得出预测寿命。并与构造函数计算所得理论寿命进行比较验证方法的有效性，预测结果如表2 所示。

由表 2中数据可以看出，该方法可以有效地预测未失效轴承的剩余使用寿命，误差基本在 5% 以内。

3 实验验证

为了验证本文提出方法的有效性，采用轴承加速退化振动实验信号进行验证分析。使用美国辛辛那提大学公开的轴承全寿命周期加速性能退化实验数据进行分析。实验台和传感器布置如图 6 所示。旋转轴由 4 个 Rexhord ZA‐2115 双列滚动轴承支撑，每个轴承的轴承座上均安置传感器并同时采集数据。径向施加 6000 LBS（26671 N）的载荷，以加快轴承退化过程。每隔 10 min 采集一次数据，采样率为 20 kHz，采样长度为 20480 个点，到实验结束时共采集了 6324 次数据，总时长约为 1055 h。

本文采用第 3 组的 4 个轴承信号进行实验验证，绘制轴承实验信号振动波形图与健康指标图分别如图 7 和 8 所示。

从图 7 中的时域振动信号可以看出，实验信号的信噪比较低，无法直观地得到信号开始退化的趋势，需要对实验数据进行特征提取。

实验信号的数据长度为 20480×6324，对每一次采样的数据进行特征提取，得到 1×6324长度的特征向量。图 8为 4组轴承实验信号退化部分的趋势图。

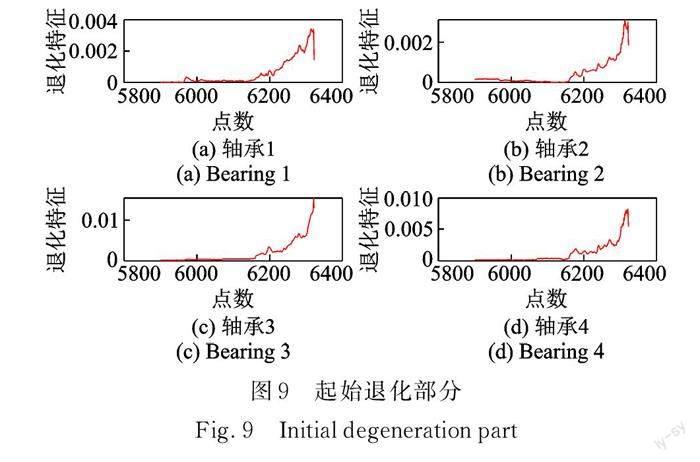
实验信号的信噪比低于仿真信号，但是使用本文方法仍然能有效从中提取出退化趋势，从图 8 中可以明显看出轴承退化状态与健康状态。为放大退化起始部分的数据变化趋势，截取全生命周期退化部分的数据，如图 9 所示。

应用一次函数拟合与阈值报警技术确定轴承退化起始点，并选取退化信息。表 3 为轴承振动实验信号退化信息。

将轴承退化部分随机截断，截断时刻之前的数据作为测试数据查询字典预测寿命，截断时刻之后的数据与预测结果对比，验证本文方法的有效性。

表 4 为测试轴承的寿命预测结果。

虽然轴承实验信号波动较大，对寿命预测存在干扰，但该方法仍能以较高的准确度预测剩余寿命。针对同一组数据本文进行了追踪预测，即对同一组数据的不同时刻进行寿命预测，并与真实寿命对比，验证该方法的预测精度。预测结果如图 10 所示。

从图 10 中可以看出，改进后的相似性预测方法在一定程度上提升了传统方法的预测精度。预测结果基本处于 30% 的误差以内，改进的方法可以有效解决轴承信号后期波动较大所带来的的预测困难。

4 结 论

通过轴承仿真及实验故障信号分析表明，使用改进相似性方法进行轴承剩余寿命预测是可行的，主要结论如下：

（1）提出了 GMM 与 JRD 结合的特征提取方法，可以有效地从轴承振动信号中提取退化分量。所提健康指标对轴承早期退化较为敏感，轴承故障后期的退化趋势随机波动较小。

（2）通过脉冲函数与双指数函数构建了轴承全生命周期仿真信号，消除了小样本数据导致预测精度较低的影响。

（3）采用一次函数拟合与滑移窗口算法结合求解出每组轴承退化数据的开始退化点，剔除了大量不包含退化信息的健康阶段数据，提高了相似性预测结果的可信度，并且减少了相似性预测的冗余计算量。

（4）根據仿真与实验结果分析，本文提出的高斯函数拟合与参数相似性结合方法可以有效地提高相似性度量的准确性，明显地提升寿命预测的精度。综上所述，改进的相似性方法可以解决参考样本不足、退化波动大、相似性度量不精确等问题。实验数据测试结果表明，该方法可以有效地预测滚动轴承剩余使用寿命。

参考文献：

［1］ Idriss El-Thalji， Erkki Jantunen. Dynamic modelling ofwear evolution in rolling bearings［J］. Tribology Interna‐tional，2015，84：90-99.

［2］ Cui L， Wang X， Wang H， et al. Remaining useful lifeprediction of rolling element bearings based on simulat‐ed performance degradation dictionary［J］. Mechanismand Machine Theory，2020，153：103967.

［3］ Zhang B， Zhang S， Li W. Bearing performance degra‐dation assessment using long short-term memory recur‐rent network［J］. Computers in Industry，2019，106：14-29.

［4］ Wang Dong， Tsui K L. Statistical modeling of bearingdegradation signals［J］. IEEE Transactions on Reliabili‐ty，2017，66（4）：1331-1344.

［5］ Ga？perin M， Juri？i？ ？， Bo？koski P， et al. Model-basedprognostics of gear health using stochastic dynamicalmodels［J］. Mechanical Systems and Signal Processing.2011，25（2）：537-548.

［6］ Medjaher K， Zerhouni N， Baklouti J. Data-driven prog‐nostics based on health indicator construction： applica‐tion to PRONOSTIAs data［C］. European ControlConference， Zürich， Switzerland. 2013：1-6.

［7］ Ocak H， Loparo K A， Discenzo F M. Online trackingof bearing wear using wavelet packet decomposition andprobabilistic modeling： a method for bearing prognostics［J］. Journal of Sound and Vibration，2007，302（4-5）：951-961.

［8］ You Mingyi. A predictive maintenance system for hy‐brid degradation processes［J］. International Journal ofQuality and Reliability Management，2017，34（7）：1123-1135.

［9］ You Mingyi. Predictive component availability optimiza‐tion with degradation correlated maintainability［J］. Pro‐ceedings of the Institution of Mechanical Engineers，Part E： Journal of Process Mechanical Engineering，2013，227（4）：243-253.

［10］ Liu J， Djurdjanovic D， Ni J， et al. Similarity basedmethod for manufacturing process performance predic‐tion and diagnosis［J］. Computers in Industry，2007，58（6）：558-566.

［11］ Liu Z， Wang Q， Song C， et al. Similarity-based differ‐ence analysis approach for remaining useful life predic‐tion of GaAs-based semiconductor lasers［J］. IEEE Ac‐cess，2017，5：21508-21523.

［12］ You M Y， Meng G. Toward effective utilization of simi‐larity based residual life prediction methods： weight allo‐cation， prediction robustness， and prediction uncertainty［J］. Proceedings of Institution of Mechanical Engi‐neers， Part E： Journal of Process Mechanical Engineer‐ing，2013，227（1）：74-84.

［13］ Gu M， Chen Y. Two improvements of similarity-basedresidual life prediction methods［J］. Journal of Intelli‐gent Manufacturing，2019，30：303-315.