高超声速飞行器自适应鲁棒跟踪滤波算法
梁新茹,高长生,荆武兴
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引 言
近些年来,高超声速飞行器因其自身具有机动能力强、机动范围广、能够长时飞行等特点,引起了越来越广泛的关注[1-3]。与传统飞行器相比,高超声速飞行器具有飞行空域复杂、飞行范围广等特性[4-5],导致在高超声速飞行器跟踪过程中探测噪声获取的统计信息不准确,同时探测噪声容易产生异常值,使得实际测量噪声呈现出非平稳非高斯特性。
针对实际噪声呈现非平稳非高斯这一问题,文献[6]指出闪烁噪声作为非高斯噪声中的一种特殊分布,通常是由异常值引起的,其分布具有重尾特性[7]。但是在传统的滤波框架内,通常假设噪声分布为高斯分布[8-9]。针对探测过程中出现的异常值问题,先验的高斯噪声建模将会损失建模的精度,使得建模成本和建模误差大大增加。针对重尾分布建模问题,目前主要采用学生t (Student’s t, ST)分布及其鲁棒算法进行描述。文献[10]指出多元ST分布能够为具有异常值的数据提供更为完善的描述,ST分布可以把高斯分布当作一种特殊情况包含在内。文献[11]提供一种基于ST分布近似噪声分布的后验概率密度函数(Probability density function, PDF)的滤波算法。文献[12]设计了一种ST分布与粒子滤波相结合的策略。但是对于非平稳重尾噪声分布来说,单一的ST分布难以准确地描述。文献[6,13]提出一种混合概率可自适应变化的高斯-学生t混合(Gaussian-student’s t mixture, GSTM)分布以适应噪声的非平稳变化。但是上述文献均没有考虑噪声先验信息未知的情况,且需要噪声的先验信息,才能保证算法的成立。
高超声速飞行器飞行空域广,空域环境复杂,导致噪声的先验统计信息复杂,噪声可能是时变、多峰的,无法给出准确的先验统计信息。针对这一问题,文献[14-16]提出利用逆Wishart分布对噪声的协方差进行建模,以解决噪声统计特性不精确的问题。文献[17]在协方差建模的基础上,进一步提出将噪声的均值和协方差联合分布近似为独立的高斯-逆Wishart分布。文献[18]将逆Wishart分布和ST建模结合,文献[19]将高斯-逆Wishart分布应用在ST建模中,完成对噪声的建模。同时,为了进一步提高滤波算法对于时变且先验信息未知噪声的鲁棒性,需要解决ST分布中自由度采用固定常值这一问题,文献[20]不再采用固定的自由度参数,而是用伽马函数来刻画自由度参数,提高了算法对于测量异常值的鲁棒性。
本文针对复杂空域飞行的高超声速飞行器探测过程出现的噪声异常值干扰,以及异常值的随机不确定性导致量测噪声的非平稳非高斯与统计信息未知一系列问题,在GSTM分布的基础上提出了一种改进鲁棒高斯-学生t混合分布滤波(Robust Gaussian-student’s t mixture distribution filtering, RGSTMF)算法。首先,引入了GSTM分布,使得算法能够自适应地调整模型概率来适应高超声速飞行器探测噪声的非平稳特性。其次,结合高斯-逆Wishart分布,利用伽马函数对GSTM分布进行改进,改进后的GSTM分布可以利用高斯-逆Wishart分布代替GSTM中的零均值假设来描述实际应用中的均值未知且时变的噪声。伽马函数代替了原有GSTM分布中固定的自由度以解决噪声非高斯程度不确定的问题。因此,改进后的GSTM分布可以实现在测量噪声先验统计信息未知的情况下,对噪声进行准确建模。最后,将改进后的GSTM分布与变分贝叶斯算法相结合,推导出RGSTMF滤波算法中参数后验更新的显式表达式,从而构成完整的滤波算法。
1 高超声速飞行器助推滑翔段建模
本文主要对高超声速飞行器助推滑翔段的跟踪问题进行研究,以HTV-2飞行器作为典型代表。参考文献[21-22],在弹道坐标系下对高超声速飞行器滑翔段建模,得到公式如下:
(1)
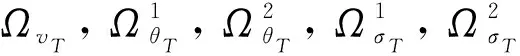
(2)
式中:关于升力系数CL和阻力系数CD的计算,本文引用文献[23]中的数据,将CL和CD拟合成马赫数Ma和攻角αT的函数,如下:
CL=-0.177 3+0.046 4αT+0.085 6e0.032 1Ma+
(3)
(4)
本文的大气密度采用指数模型
ρT(h)=ρ0e-h/H
(5)
式中:ρ0取值为ρ0=1.46×10-3kg/m3;H=6 970 m。
地球自转相关的高阶项如下:
(6)
式中:ωe表示地球自转角速率的大小。
2 RGSTMF算法
2.1 GSTM分布
在高超声速飞行器实际跟踪过程中,由于目标特性和飞行环境的复杂性,跟踪量测值极易出现异常值,这将导致噪声分布的非高斯闪烁特性。因此引入GSTM分布对噪声进行建模,GSTM分布公式如下:
pN(x)=N(x;μ,Σ)
(7)
pST(x)=ST(x;μ,Σ,v)
(8)
pGSTM(x)=δpN(x)+(1-δ)pST(x)
(9)
式中:N(·)表示高斯分布;μ表示分布的均值;Σ表示分布的协方差;ST(·)表示ST分布;v表示ST分布的自由度;δ表示混合概率。
参考文献[6],混合概率δ满足
p(δ)=B(δ;e,1-e)
(10)
式中:B(·)表示Beta分布;e表示Beta的先验形状参数。
从式(9)中可以看出当混合概率δ=1时,GSTM分布服从高斯分布,当混合概率δ=0时,GSTM分布表现为ST分布,因此高斯分布和ST分布是GSTM分布的一种特殊形式。GSTM分布在应对非平稳噪声方面具有一定的优势,具有更加广泛的应用。
引入隐变量ξ,式(9)可以被改写为
pGSTM(x|ξ)=δN(x;μ,Σ)+(1-δ)N(x;μ,Σ/ξ)
(11)
式中:隐变量ξ满足
(12)
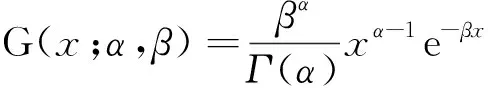
因为噪声统计特性未知且时变,固定自由度参数v的使用会导致噪声建模的不准确性,因此,将自由度参数v建模成为伽马函数[18]。
引用伯努利随机变量y,式(11)可以被改写为
pGSTM(x|ξ,y)=[N(x;μ,Σ)]y+
[N(x;μ,Σ/ξ)](1-y)
(13)
式中:伯努利随机变量y满足
p(y|δ)=δy(1-δ)y
(14)
因此,式(9)可以写作
p(ξ|v)p(δ)p(v)dξdys.t.y∈{0, 1}
(15)
式中:关于隐变量ξ的积分为定积分,关于伯努利随机变量y的积分为不定积分,使得最终的积分结果为y的函数,用于积分外侧的求和运算。
2.2 问题描述
构建高超声速飞行器非线性跟踪系统:
xk=f(xk-1)+ωk-1
(16)
zk=h(xk)+υk
(17)
式中:xk∈Rn表示k时刻的状态向量;f(·)表示状态函数;h(·)表示量测函数;zk∈Rm表示k时刻的量测向量;wk-1表示系统噪声,满足高斯分布;υk表示量测噪声。
对于高超声速飞行器来说,由于飞行器飞行空域复杂,目标特性复杂,在跟踪过程中,容易出现异常值,这会导致目标的量测噪声出现非高斯特性。同时由于异常值的非平稳特性,导致目标量测噪声存在统计特性未知的情况。因此,在实际应用过程中,量测噪声υk的表达形式和统计信息没有先验的假设,量测噪声υk可能是非高斯分布,甚至可能是多峰的、倾斜的分布。本文的目的是在没有先验统计特性信息的条件下,对量测噪声进行建模,在此基础上推导完成滤波算法。
2.3 先验分布的选择
根据贝叶斯公式,为了求解滤波的后验状态估计,需要对一步预测和似然函数进行建模。
由于过程噪声的高斯特性,将一步预测建模为高斯分布:
p(xk|z1:k-1)=N(xk;xk/k-1,Pk/k-1)
(18)
式中:xk/k-1表示k时刻状态估计的一步预测均值;Pk/k-1表示k时刻状态估计的一步预测协方差,同时,下文中出现的下角标(·)k/k-1均表示该参数(·)的一步预测值,下角标(·)1:k-1表示该参数(·)的1~k-1时刻的值。
由于测量过程中异常值的影响,量测噪声呈现出非高斯特性,因此利用GSTM分布来刻画似然函数。同时考虑到在目标测量时,飞行器的飞行空域和自身辐射特性的复杂性会导致量测信息统计特性未知,因此将量测噪声建模成均值未知且时变的GSTM分布,根据量测噪声得到似然函数建模公式如下:
[N(xk;h(xk)+Ak,Βk/ξk)](1-yk)·
p(δk)p(vk)dξkdyks.t.yk∈{0,1}
(19)
式中:与式(15)相同,隐变量ξk的积分为定积分,关于伯努利随机变量yk的积分为不定积分,使得最终的积分结果为yk的函数,用于积分外侧的求和运算。Ak和Βk分别表示量测噪声均值和协方差,参考文献[17],将均值和协方差的联合函数建模成为高斯-逆Wishart分布,公式如下:
p(Ak|Bk)=N(Ak;ak/k-1,bk/k-1Bk)
(20)
p(Bk|z1:k-1)=IW(Bk;uk/k-1,Uk/k-1)
(21)
式中:IW(·)表示逆Wishart分布,公式如下
IW(B;λ,Ψ)=
(22)
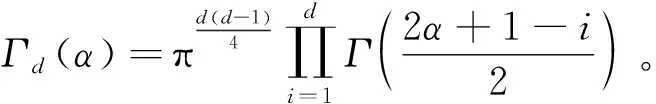
根据2.1小节中的建模思路,将ST分布中的自由度参数vk表示为伽马分布。
p(vk)=G(vk;ck/k-1,dk/k-1)
(23)
混合概率δk满足p(δk)=B(δk;e0,1-e0),其中,e0∈[0,1]表示PDFp(δk)的先验形状参数。
根据上文的建模,得到相对应的概率图模型,如图1所示。
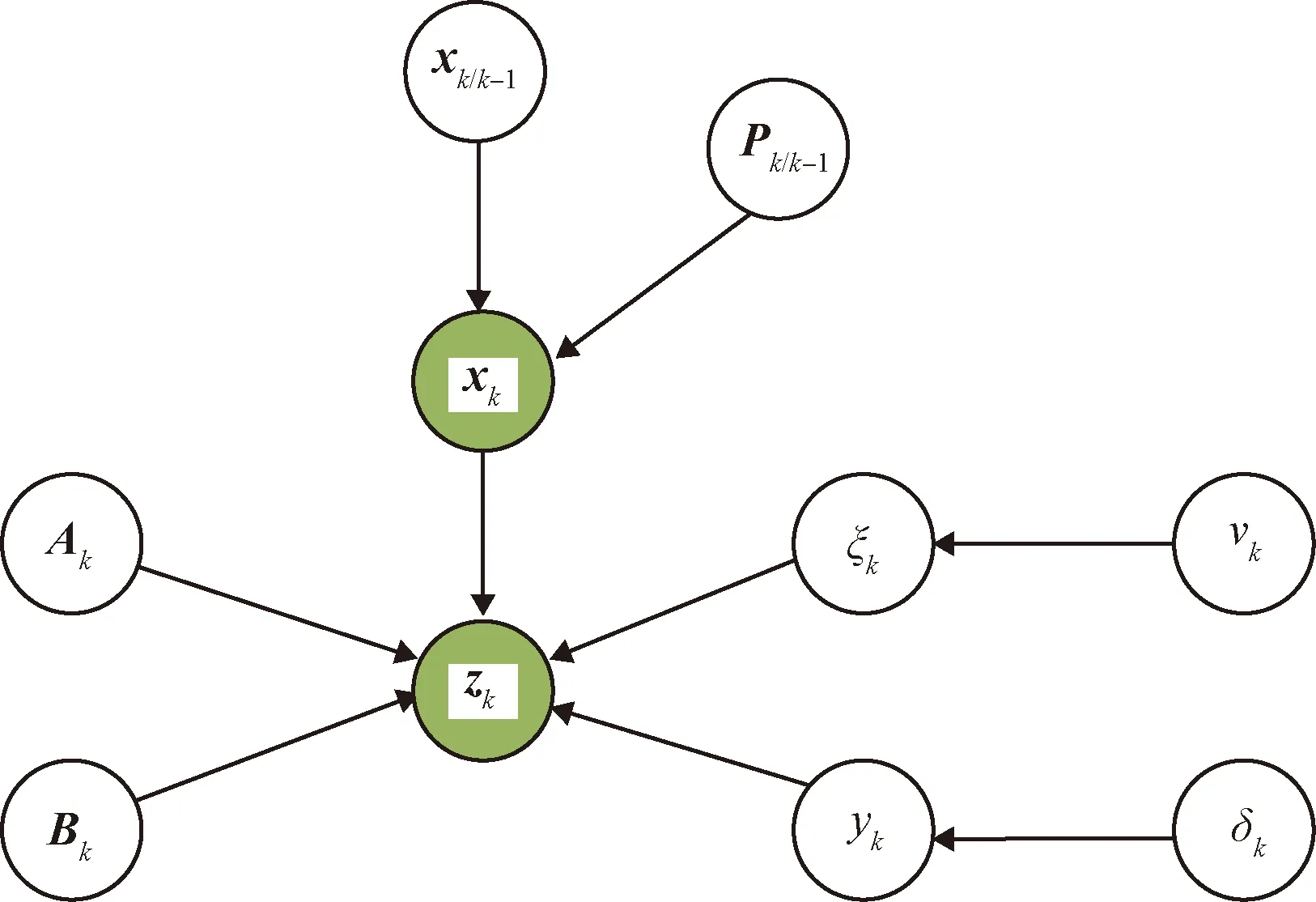
图1 概率图模型Fig.1 Graphical model
在Kalman滤波框架内,已知一步预测的建模,利用容积滤波器(Cubature Kalman filter, CKF)滤波方法得到时间更新方程:
(24)
(25)
式中:Qk-1表示过程噪声协方差;2m表示粒子数;ζi和wi的计算公式如下
Sk-1/k-1=chol(Pk-1/k-1)
(26)
(27)
(28)
式中:chol(·)表示Cholesky分解,[1]i表示点集[1]的第i组列向量,[1]=[Im,-Im],Im为m维的单位矩阵。
在飞行器滤波跟踪算法的实际应用过程中,p(Bk|Bk-1),p(Ak|Ak-1),p(vk|vk-1)无法获取,本文参考文献[24],引入遗忘因子ρ来描述系统的动态不确定性,ρ的取值范围为[0.9,1)。
uk/k-1=ρ(uk-1/k-1-md-1)+md+1
(29)
Uk/k-1=ρUk-1/k-1
(30)
ak/k-1=ak-1/k-1,bk/k-1=ρbk-1/k-1
(31)
ck/k-1=ρck-1/k-1,dk/k-1=ρdk-1/k-1
(32)
式中:md表示矩阵维度。
2.4 后验分布的变分逼近
根据2.3小节中对于一步预测和似然函数的建模,为了得到滤波算法的量测更新,需要对联合后验PDFp(Θk|z1:k)进行推导,其中Θk包含一步预测和似然函数中的未知参数,定义Θk为变分变量,Θk={xk,Ak,Βk,yk,δk,ξk,vk}。
2.4.1变分贝叶斯
由于联合后验PDF中各参数的耦合,对于后验参数的估计难以得到解析解,因此,引入变分贝叶斯(Variational Bayesian, VB)算法[25],利用自由因子分布近似联合分布,联合后验PDFp(xk,Ak,Βk,yk,δk,ξk,vk|z1:k)可以写作:
p(Θk|z1:k)≈q(xk)q(Ak)q(Βk)q(yk)q(δk)·
q(ξk)q(vk)
(33)
式中:q(·)表示p(·)的近似后验概率分布。
为了得到后验PDF,需要最小化q(xk),q(Ak),q(Βk),q(yk),q(δk),q(ξk),q(vk)和联合后验PDFp(Θk|z1:k)之间的Kullback-Leibler散度(Kullback-Leibler divergence, KLD)[26]。
{q(xk),q(Ak),q(Βk),q(yk),q(δk),q(ξk),q(vk)}=
argmin KLD(q(xk),q(Ak),q(Βk),q(yk),
q(δk),q(ξk),q(vk)||p(Θk|z1:k))
(34)
式中:KLD用来衡量两个概率分布之间的差异程度[27],计算公式为:
(35)
根据式(35)可以看出,当两个概率分布之间的差异性越小,KLD越小,因此,可以通过最小化KLD,求取概率分布p(x)的近似分布q(x)。
根据VB计算方法,式(34)的最优解满足下面的公式[24]:
lnq(θ)=EΘ(-θ)[lnp(Θk,z1:k)]+cθ
(36)
式中:θ∈Θ并且满足Θ(-θ)∪θ=Θ;cθ表示独立于θ的常值。
由于Θ中的各个参数之间相互耦合,无法直接得到其解析解,因此需要定点迭代求解式(36)。利用q(j)(Θ(-θ))的结果,近似求解后验PDFq(θ)在j+1次迭代时的PDFq(j+1)(θ),直到收敛到式(36)的局部最优值[24]。下面在2.4.2小节中推导各个参数的迭代更新过程。
2.4.2变分迭代过程
已知联合分布p(Θk,z1:k)可以被分解为
p(Θk,z1:k)=p(z1:k-1)N(xk;xk/k-1,Pk/k-1)·
[N(xk;h(xk)+Ak,Βk)]yk[N(xk;h(xk)+
Ak,Βk/ξk)](1-yk)N(Ak;ak/k-1,bk/k-1Bk)·
IW(Bk;uk/k-1,Uk/k-1)δkyk(1-δk)ykB(δk;e0,
(37)
1) 令θ={Ak,Bk}
在第j+1次循环时,{Ak,Bk}的联合后验PDF更新为高斯-逆Wishart分布:
(38)
式中:下角标(·)k/k均表示该参数(·)的估计值。
(39)
(40)
式中:E(j)[x]表示参数x在j次迭代后的数学期望。
(41)
(42)
(43)
(44)
式中:
(45)
Sk/k-1=chol(Pk/k-1)
(46)
(47)
(48)
2) 令θ={yk}
在第j+1次循环时,yk的后验PDF更新为Bernoulli分布:
(49)
(50)
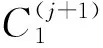
(51)
根据式(49)~(51)和Bernoulli分布的性质,可以求解得到:
(52)
3) 令θ={δk}
在第j+1次循环时,δk的后验PDF更新为Beta分布
(53)
式中:
(54)
(55)
根据式(53)~(55)和Beta分布的性质,可以求解得到:
(56)
(57)
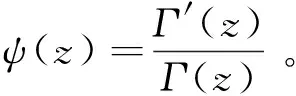
4) 令θ=(ξk)
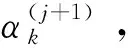
(58)
式中:
(59)
(60)
根据式(58)~(60)和伽马分布的性质,可以求解得到:
(61)
(62)
5) 令θ={vk}
在第j+1次循环时,vk后验PDF更新为
(63)
式中:
(64)
(65)
6) 令θ={xk}
在第j+1次循环时,xk的后验PDF更新为
(66)
式中:
(67)
(68)
(69)
(70)
式中:
(71)
(72)
3 仿真校验
3.1 高超声速飞行器HTV-2的建模仿真
根据小节1中对高超声速飞行器HTV-2助推滑翔段的动力学描述,以及考虑飞行器在实际飞行过程中的飞行走廊约束,完成对HTV-2的弹道规划[28-29]。
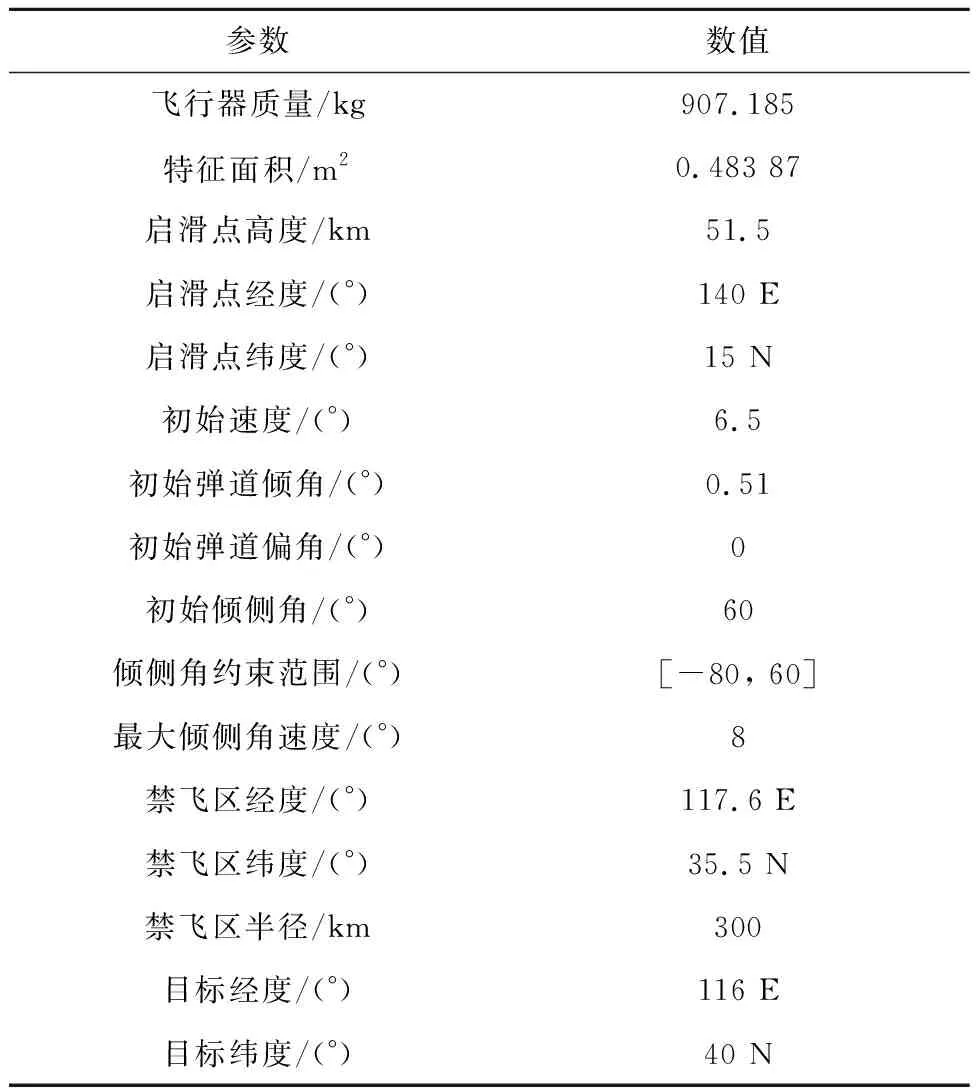
表1 HTV-2高超声速飞行器弹道仿真参数Table 1 Trajectory simulation parameters of hypersonic vehicle HTV-2
仿真结果图弹道如图2所示:
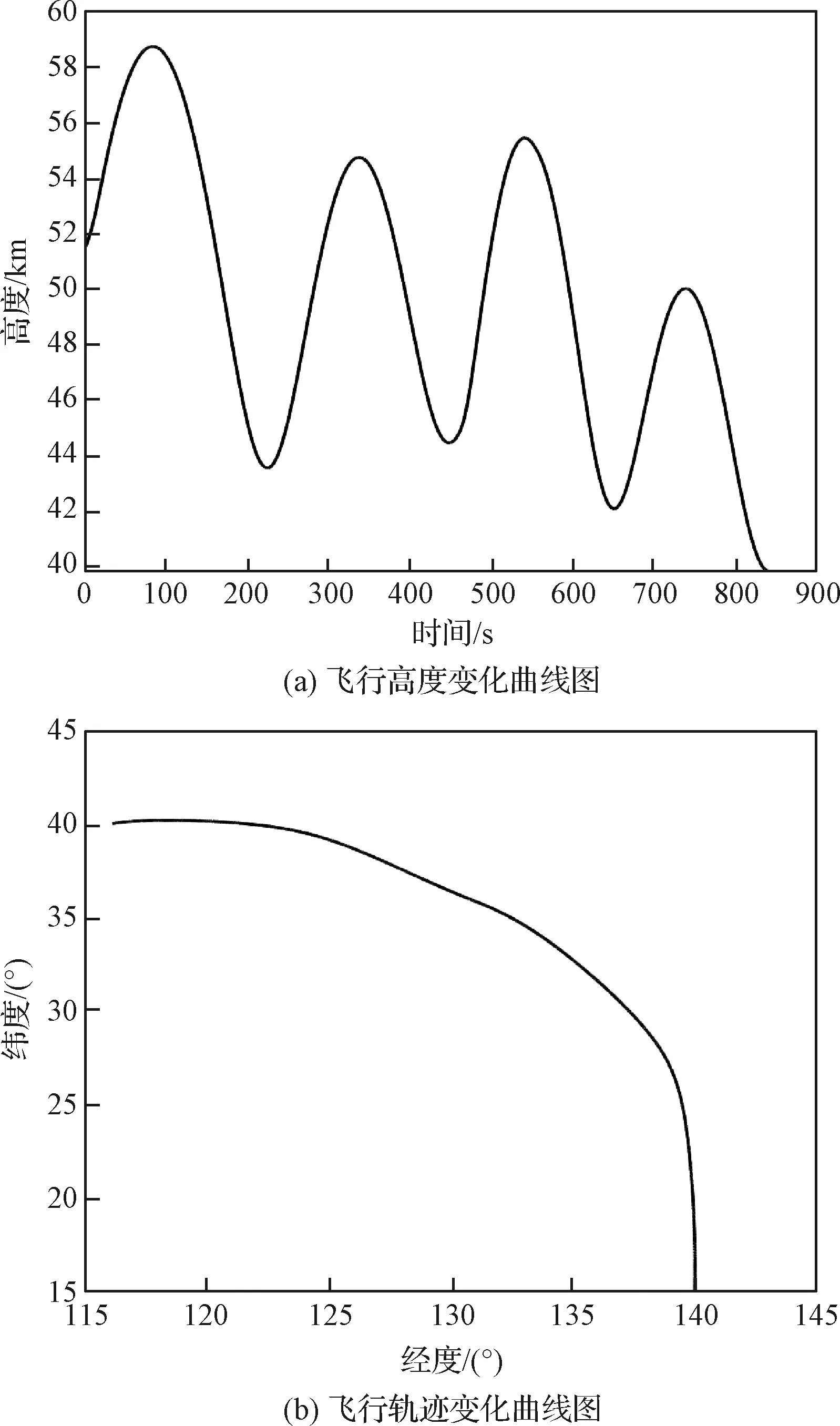
图2 弹道形态Fig.2 Ballistic configuration
3.2 仿真场景设置
采用地基雷达观测,观测方程如下:
(73)
式中:Aak,Eek,Rrk分别为雷达探测的高低角方位角和斜距;υk为量测噪声。
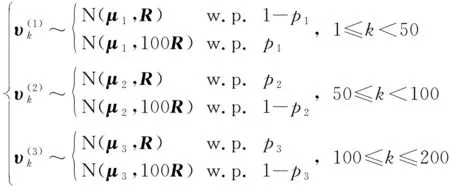
(74)
式中:w.p.表示“with probability”;p1,p2,p3表示异常值概率。R表达式如下:
(75)
式中:σA=σE=0.03°,σR=20 m。
(76)
根据第1小节对高超声速飞行器的动力学建模分析,在高超声速飞行器的滑翔段,飞行器主要受重力和气动力的控制,因此可以从动力学的角度出发,设计合理的模型参数对动力学进行建模,利用扩维后的动力学模型进行状态估计[8,28,30-31]。
本文参考文献[28],采用弹道系数模型作为跟踪模型。定义弹道系数为
(77)
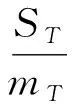
(78)
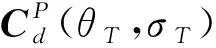
为了比较不同算法对目标的状态估计精度,给出状态的均方根误差(RMSE)和平均均方根误差(ARMSE)的定义如下:
RMSEk,X=
(79)
ARMSEX=
(80)
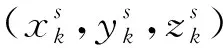
为了对比算法的估计性能,本文对比了5种滤波算法:传统的CKF算法,量测噪声采用高斯建模的自适应变分贝叶斯容积卡尔曼滤波(Adaptive variational Bayesian cubature Kalman filtering, AVBCKF-R)算法[32],采用ST建模的鲁棒变分贝叶斯学生t滤波(Robust variational Bayesian Student’s t filt-ering, RVBST)算法[33],未包含测量统计信息建模的GSTMF算法[6],以及本文中提出的改进RGSTMF算法。同时,为了更好地比较GSTM分布的建模优势,将AVBCKF-R算法和RVBST算法中的噪声均值按照本文提出的方法进行建模。
3.2.1仿真场景1
在仿真场景1中,设置噪声异常值变化幅度较小且变化平缓,设置异常值概率分别为:p1=0.01,p2=0.02,p3=0.04。在场景1中设置异常值所占的概率较小,噪声重尾分布较轻。仿真结果见图3~图4和表2。
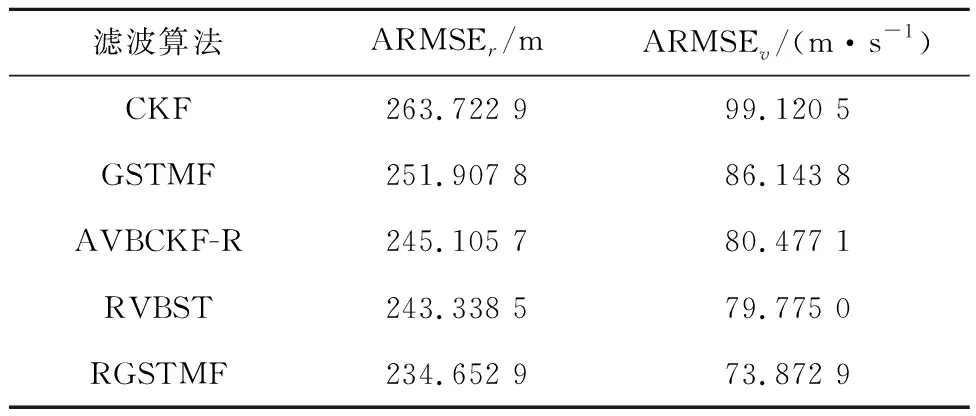
表2 不同滤波算法的ARMSEsTable 2 The ARMSEs of different filtering algorithms
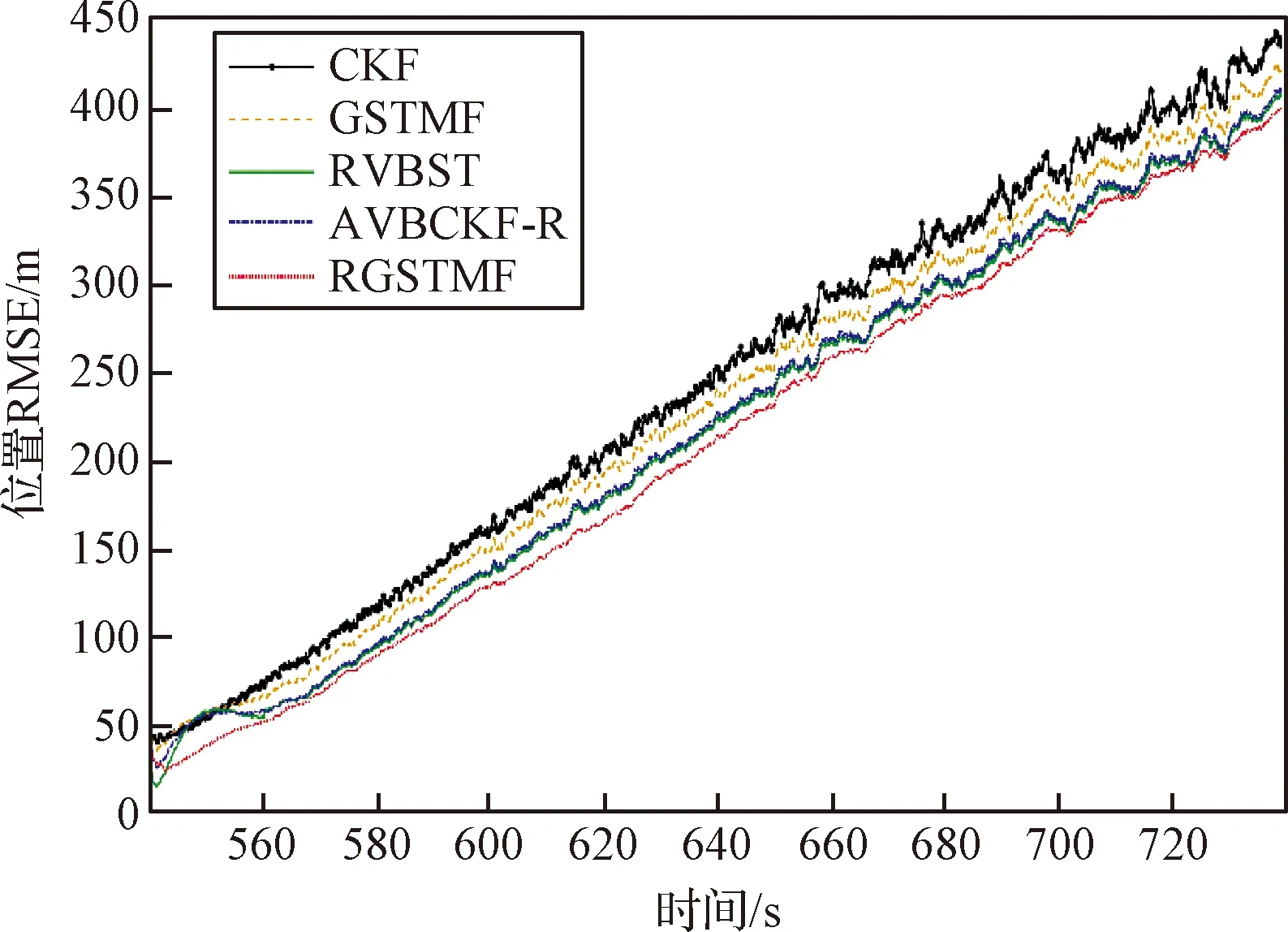
图3 位置变量的RMSEFig.3 The RMSEs of position
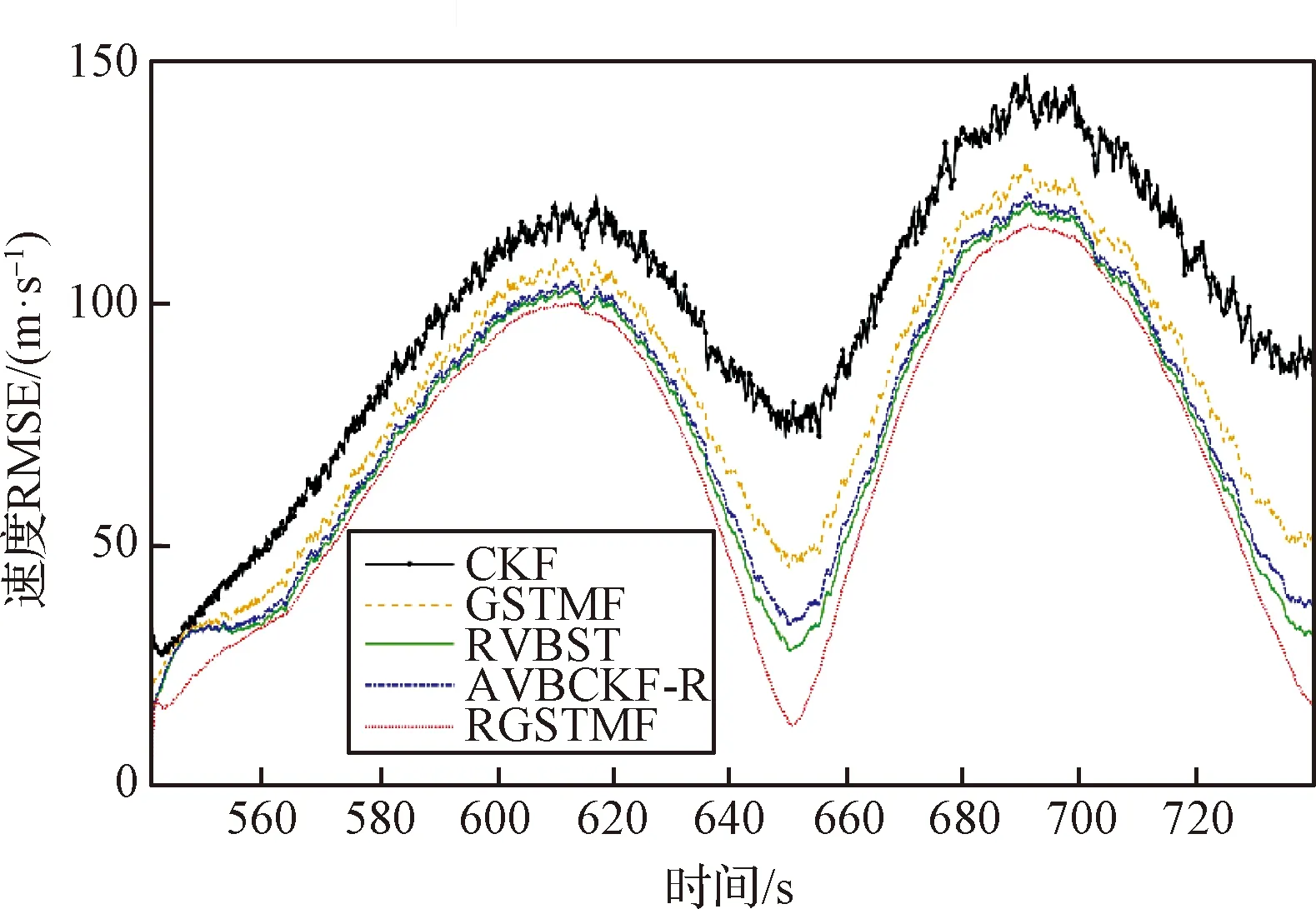
图4 速度变量的RMSEFig.4 The RMSEs of velocity
从仿真图和表格可以看出,由于缺少对噪声的建模,CKF算法精度表现最差,本文提出的RGSTMF算法精度最优。同时可以看出,与噪声高斯建模的AVBCKF-R算法和ST建模的RVBST算法相比,本文提出的RGSTMF算法精度更高,这说明GSTM分布与高斯分布和ST分布相比,能更好地拟合非平稳噪声,这与文献[5]中的结论一致。此外,与文献[5]中的GSTM算法相比,RGSTMF算法包含对噪声统计特性的描述,因此在面对统计信息未知的量测噪声时,具有更好的鲁棒性和更高的计算精度。
3.2.2仿真场景2
在仿真场景2中,设置噪声变化幅度较大,设置异常值概率分别为:p1=0.1,p2=0.2,p3=0.4。在场景2中设置异常值所占的概率较大,噪声重尾程度较重。仿真结果见图5~图6和表3。
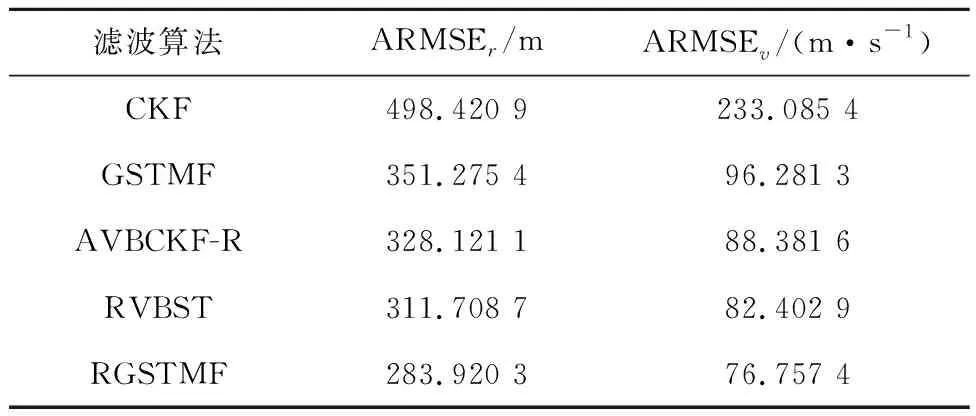
表3 不同滤波算法的ARMSETable 3 The ARMSEs of different filtering algorithms
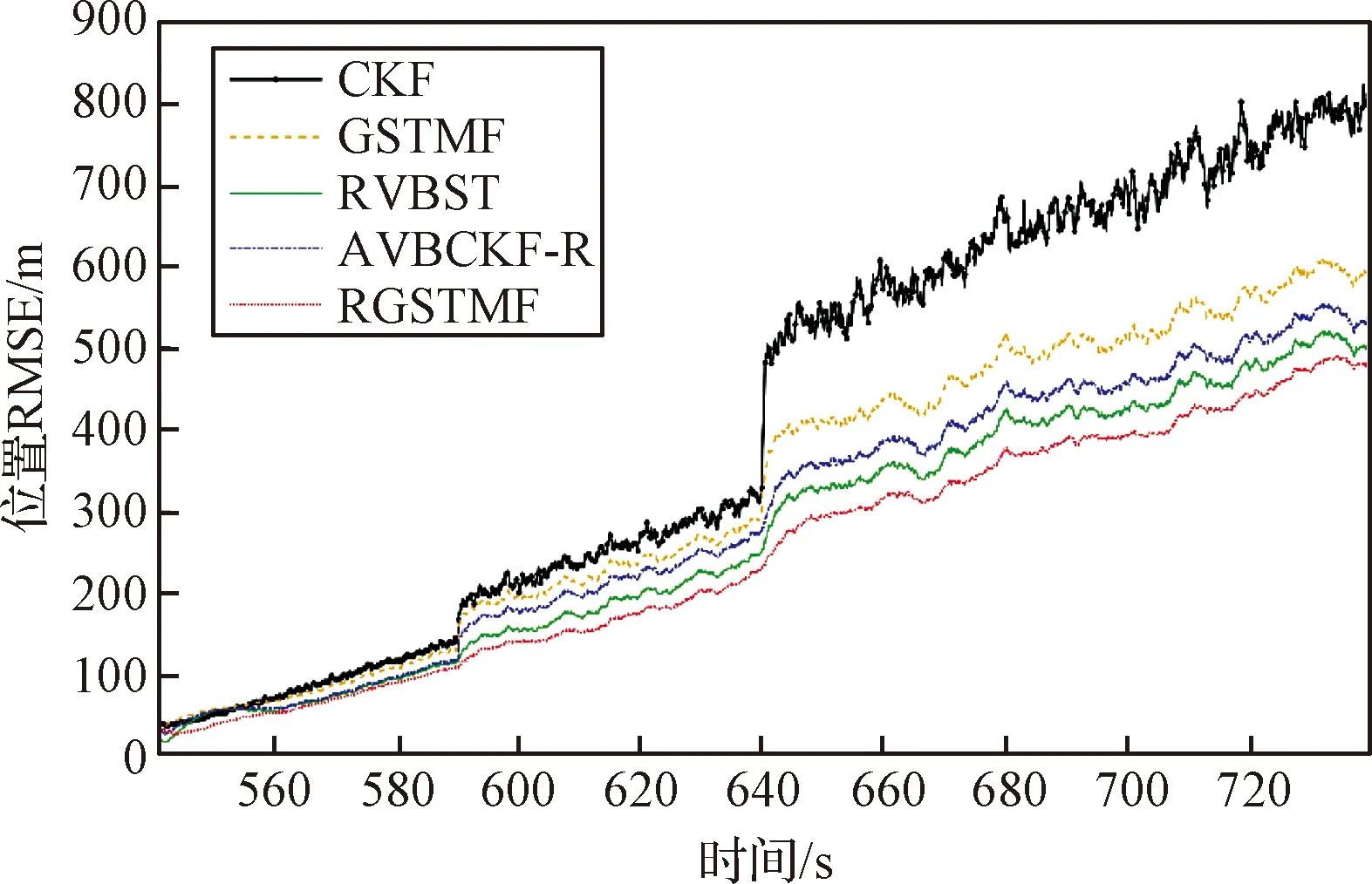
图5 位置变量的RMSEFig.5 The RMSEs of position
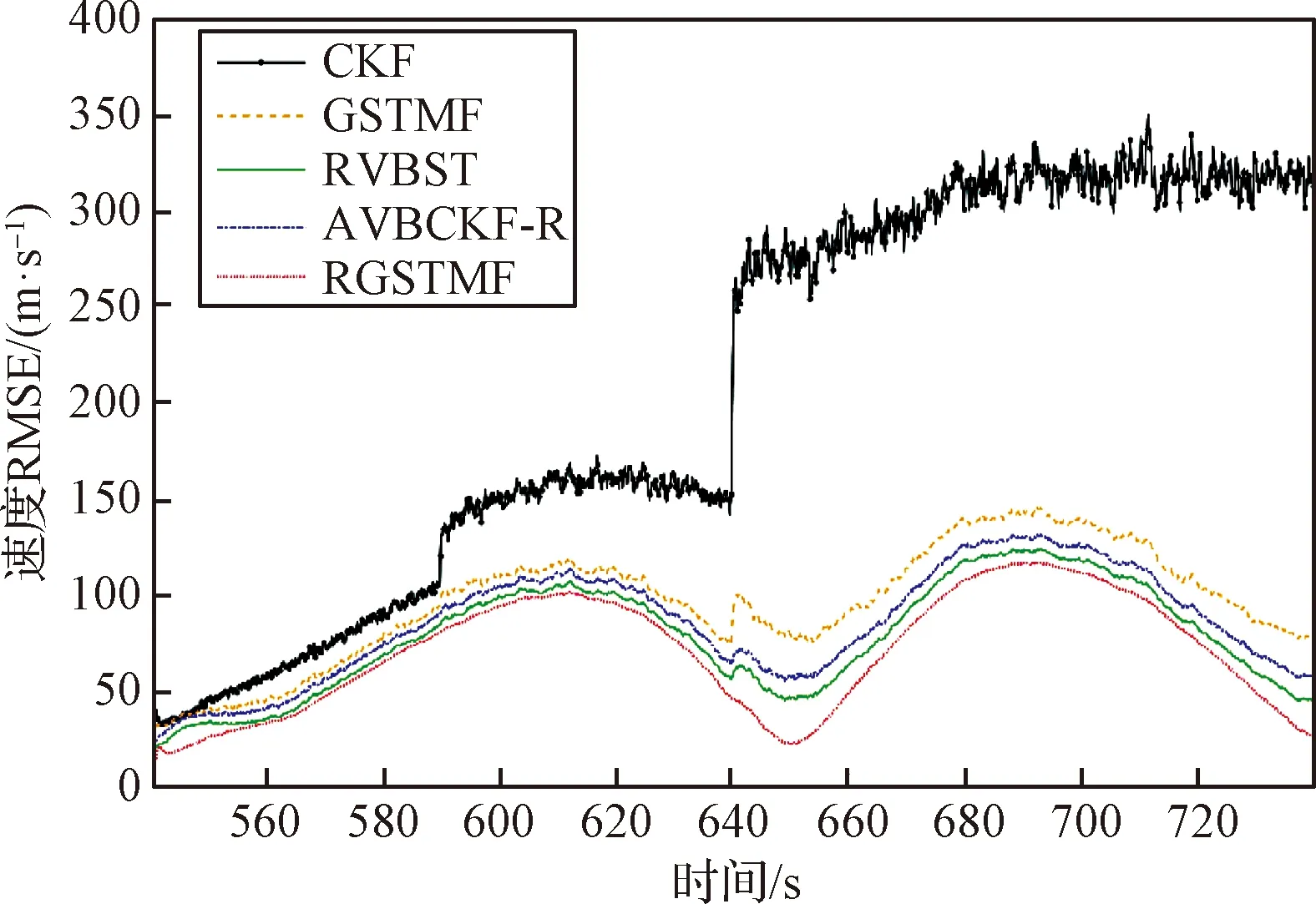
图6 速度变量的RMSEFig.6 The RMSEs of velocity
从仿真图可以看出,在噪声异常值进一步增加的情况下,CKF算法已经出现了较大的误差,GSTM分布的误差也进一步加大,而文中所提出的RGSTMF算法仍然能保持较高的精度。
综合仿真1和仿真2,可以看出对比现有的滤波算法,本文所提出的RGSTMF算法滤波精度最高。与噪声高斯建模的AVBCKF-R算法和ST建模的RVBST算法相比,所提出的RGSTMF算法无论是在面对异常值概率较低、变化较为缓慢的噪声分布,还是异常值占比较高、噪声突变的噪声分布,都能够表现出较为良好的跟踪精度,这说明GSTM分布对非平稳噪声具有更好的拟合精度。同时,可以看出,采用对噪声均值建模的方法可以进一步提升RGSTMF算法的鲁棒性,使得其与CKF和GSTMF相比,能在噪声统计信息未知的情况下保持较好的跟踪精度。
3.3 遗忘因子的影响
本小节探讨影响算法的可调节参数遗忘因子ρ对算法精度的影响,仿真结果见图7和图8。
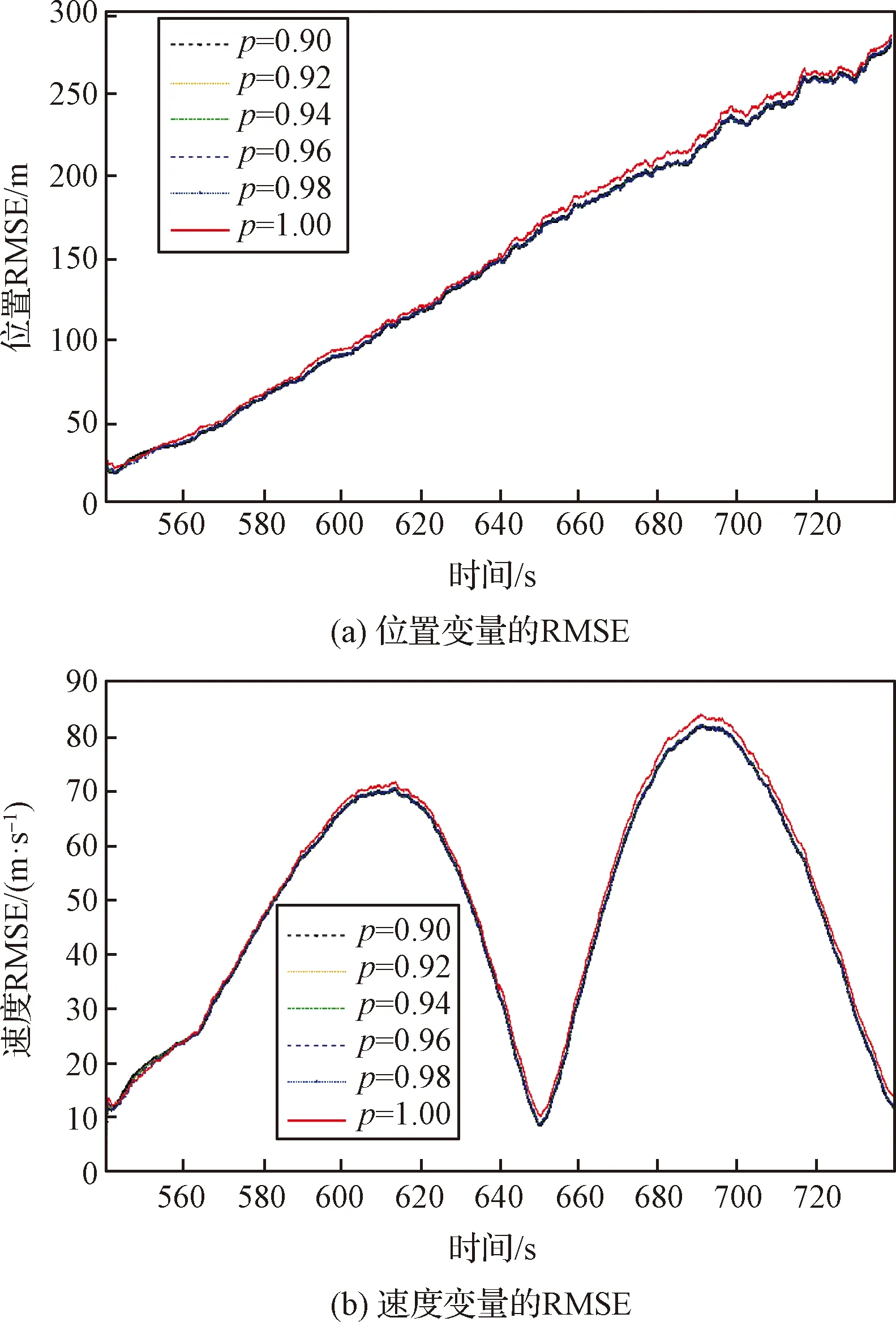
图7 场景1中不同的遗忘因子对RMSE的影响Fig.7 RMSE performances of different forgetting factors in Scenario 1
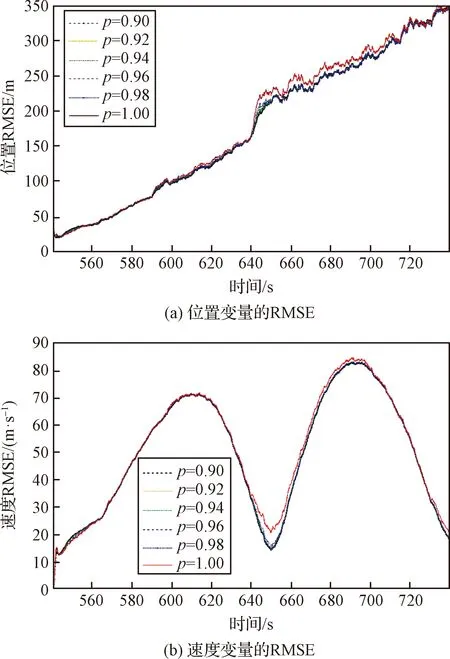
图8 场景2中不同的遗忘因子对RMSE的影响Fig.8 RMSE performances of different forgetting factors in Scenario 2
从仿真图可以看出,当遗忘因子选取为ρ=0.9,0.92,0.94,0.96,0.98时,算法的精度没有出现较大的差异,但是当算法采用ρ=1时,滤波误差开始增大,并且随着噪声异常值概率的增加,误差越明显。这是因为当ρ=1,算法p(Bk|Bk-1),p(Ak|Ak-1),p(vk|vk-1)中的参数采用固定的建模参数,难以应对时变的噪声。
4 结 论
针对高超声速飞行器飞行过程中出现的统计特性未知的非平稳非高斯探测噪声,本文提出一种改进RGSTMF算法。利用高斯-逆Wishart分布构建时变且未知的均值模型用于代替原始GSTM中的零均值假设,同时引入伽马函数分布来刻画不确定的非高斯程度,改进的RGSTM分布使得滤波算法对非平稳噪声的建模精度得到进一步的提高;将变分贝叶斯算法与RGSTM分布相结合,解析推导出了后验概率更新的显式表达式。仿真结果验证了本文提出方案的可行性,与其他先进算法相比,本文中所提出的RGSTMF算法能够在先验信息未知的情况下,更好地刻画噪声时变且未知的均值和非高斯程度,在面对统计信息未知的非平稳非高斯程度不确定的噪声时,表现出良好的鲁棒性和跟踪精度,并且随着非高斯程度的进一步增加,算法仍能保持良好的跟踪精度。

