高超声速滑翔飞行器解析协同再入制导
刘 旭,李 响,王晓鹏
(1. 北京理工大学宇航学院,北京 100081;2. 上海机电工程研究所,上海 200233)
0 引 言
高超声速滑翔飞行器因其具有飞行速度快、飞行范围广、突防能力强等特点,近年来受到研究人员的广泛关注和研究[1-2]。世界各国在加速研制高超声速滑翔飞行器的同时,也在积极推进针对该类飞行器的防御体系的建设[3]。在此背景下,单飞行器任务能力的提升逐渐进入瓶颈期,多飞行器协同制导技术得到了快速发展。与现有绝大多数文献相同,本文中的“协同”是指时间上的协同。根据飞行过程中是否存在通信,可将协同制导分为绝对时间协同制导和非绝对时间协同制导两类。前者在发射前设定好打击时间,各飞行器无通信地独立飞行,在指定时刻到达目标点即可实现时间协同的目的;后者无需预先设定,而是依靠个体间的信息交流使每个个体向协商好的目标状态靠拢,最终实现协同一致。对于再入滑翔而言,飞行过程中存在“黑障”区,飞行器之间的距离也相对较远,因此采用绝对时间协同制导更符合实际。
目前,对于末制导段协同制导的研究较为丰富。文献[4]首次将攻击时间误差反馈引入比例导引律,提出一种攻击时间控制制导(Impact time control guidance, ITCG),实现了反舰导弹对静止目标的齐射攻击;文献[5]提出一种基于滑模控制的攻击时间控制制导,利用剩余时间估计和碰撞航向的概念设计滑模面,即使在不利初始条件下也能有效实现对目标的协同打击;文献[6]在现有寻的制导律的基础上,结合剩余飞行时间预测,提出一种可以满足攻击时间约束的制导律,通过横向加速度制导指令使攻击时间误差在攻击时间范围内收敛到零;文献[7]面向具备推力控制能力的导弹提出一种约束速度上下界的协同制导律,以法向加速度为输入独立控制飞行方向,以发动机推力为输入控制协同飞行速度,实现了带攻击角度约束的齐射攻击;文献[8]分别设计了视线方向分布式协同制导律和视线法向制导律,能使所有导弹的打击时刻在有限时间内达到一致,并保证所有导弹的视线角在有限时间内收敛到期望值;文献[9]构造满足期望时间约束的虚拟命中点,将制导过程分为期望攻击角度制导和比例导引制导,基于交战几何关系计算等效最大视场角,实现了满足视场角约束和攻击角度约束的协同攻击。
对高超声速滑翔飞行器而言,再入段飞行时间要远大于末制导段[10],末制导段时间协同能力比较有限,而且依赖再入段提供良好的初始条件。因此,有必要研究多飞行器再入段协同制导,为末制导提供良好交班条件的同时,尽可能地提高整个飞行过程的时间调节范围。在大多数时间相关的制导律研究中,对剩余飞行时间的估计是制导律设计的关键。前述协同制导研究大多采用了恒定速度假设或者速度可控假设,将原动力学问题简化,从而降低剩余时间估计的计算难度。然而对高超声速滑翔飞行器而言,再入段飞行时间跨度大,速度变化明显,前面的假设显然不成立[11]。
近几年,关于高超声速滑翔飞行器协同再入制导的研究开始增多。文献[10]提出一种基于深度Q学习网络(Deep Q-learning network, DQN)的时间可控再入制导律,纵向根据当前飞行状态和攻角-速度剖面规划倾侧角幅值,横向基于深度神经网络的离线训练结果在线生成倾侧角符号;文献[11]推导出关于剩余时间和剩余距离的计算公式,并进一步分析了剩余时间、剩余距离和末速度这三个变量之间的关系,在此基础上构建了满足到达时间约束的再入制导律;文献[12]在横向剖面采用预测横向制导调整再入飞行时间,在纵向剖面设计二次倾侧角幅值剖面,并通过牛顿迭代法调节该剖面以满足剩余距离和剩余时间的约束;文献[13]基于考虑地球自转的再入动力学方程,推导出了再入飞行时间、纵程和横程的解析解,并以此为依据设计了一种多禁飞区约束下解析的多飞行器协同再入制导方法;文献[14]利用解析预测-校正思想,提出一种再入滑翔轨迹分段设计方法,在时间调整段和能量调整段调节倾侧角幅值和翻转时机,从而同时满足末端能量和时间约束;文献[15]提出一种基于参考轨迹的绝对时间协同再入制导,设计协调层将轨迹长度作为协调参数进行协调匹配,在执行层依据分配的协调参数完成再入飞行,并将终端时间的一致性问题转化为到达截止时间的状态收敛问题。
从现有研究成果可知,再入时间的可控范围越大越有利于协同再入的实现,提高时间调节能力也是再入制导的难点之一。例如,文献[11]成功实现了带时间约束的再入制导,但其时间可控范围仅有±20 s,且需要通过放宽终端速度约束来实现,这很大程度上降低了该方法的实际意义。此外,利用准平衡滑翔条件(Quasi-equilibrium glide condition, QEGC)能够很大程度上地降低再入飞行力学问题的维度和复杂性,使很多闭环形式的解决方案得以实现[16]。再入制导方法可以分为标称轨迹制导和预测校正制导两类,由于再入气动环境非常复杂,飞行时间容易受到不确定性因素的影响[17-18],因此采用预测校正制导在线预测剩余飞行时间并校正再入轨迹是更为稳妥的方案。
基于以上分析,本文针对文献[11]中可控时间范围小的不足,在准平衡滑翔条件下,将纵向升阻比视为变量,重新推导了剩余飞行时间和剩余飞行距离的解析解,并结合预测校正的思想,设计了一种满足时间约束的再入制导律,有效提高了再入时间的可控范围,最后实现了多约束条件下高超声速滑翔飞行器的协同再入制导。
1 协同再入制导问题描述
1.1 再入动力学方程
假设地球为均匀圆球,且不考虑地球自转,则多高超声速滑翔飞行器的三自由度再入动力学方程可以表示为
(1)
(2)
(3)
(4)
(5)
(6)
式中:i表示第i个飞行器;r为地心距;θ为经度;φ为纬度;v为速度;γ为航迹角;ψ为航向角;m为质量;g为重力加速度;σ为倾侧角;L为升力;D为阻力。
进一步地,升力和阻力可表示为
(7)
式中:ρ=ρ0e-h/h0为大气密度,ρ0=1.225 kg/m3为海平面大气密度,h=r-R0为飞行高度,R0为地球半径,h0为密度尺度高;S为参考面积;CL和CD分别为升力系数和阻力系数,是攻角α和马赫数Ma的函数。文献[19]综合考虑攻角和马赫数对升力系数、阻力系数的影响,给出一种改进的高超声速滑翔飞行器气动系数模型:
(8)
式中:li和di(i=0,1,…,5)为辨识出的气动系数,具体数值参见文献[19]。
1.2 约束条件
为保证再入段实现时间协同制导,并为末制导段提供良好的初始条件,终端约束包括飞行时间约束、高度约束、经度约束、纬度约束和速度约束:
(9)
式中:tf,i为第i个飞行器的终端飞行时间;tf,rf,θf,φf和vf为别为对应的终端约束值。
(10)

1.3 再入轨迹分段
为方便制导律设计,本文将再入飞行轨迹分为初始下降段、转换段和准平衡滑翔段。再入飞行器进入大气层边缘后,首先进入初始下降段。由于大气层边缘空气稀薄,处于该阶段的飞行器将快速下降。飞行器下降至拥有足够的动压以产生足够的气动力后进入转换段,并平稳过渡至滑翔段飞行。在滑翔段飞行器将维持准平衡滑翔,并飞行至目标点。滑翔段的飞行时间和飞行距离远大于下降段和转换段,同时本文的制导律基于由准平衡滑翔条件推导出的解析结果。因此,滑翔段是时间控制的关键阶段,应尽可能地缩短下降段和转换段的时间,为滑翔段留出足够的时间来进行时间控制。
2 剩余飞行时间和剩余飞行距离估计
接下来讨论基于准平衡滑翔条件的剩余飞行时间tgo和剩余飞行距离sgo估计方法[21],这是本文提出的考虑时间约束的制导方法的基础。
2.1 剩余飞行时间估计
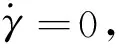
(11)
由于高度h远小于R0,假定R0/r=1,同时认为g=g0不变,整理式(4)和式(11)并积分可得:
(12)
令c=(L/D)cosσ,表示升阻比的纵向分量。与文献[11]中假设c为常数不同,本文假设c为速度v的一次函数,可表示为
c=k0+k1v
(13)
将式(13)代入式(12)可得剩余时间估计的解析表达式为
(14)
2.2 剩余飞行距离估计
将剩余飞行距离sgo定义为连接飞行器当前位置和终端目标位置的地球表面大圆弧弧长,忽略该大圆弧方向角与飞行器方向角之间的误差,sgo的变化率可表示为[20]
(15)
与前述假设相同,并将式(4)代入式(15)可得:
(16)
同样地,整理式(11)和式(16)并积分可得:
(17)
将式(13)代入式(17)可得剩余距离估计的解析表达式为
(18)
需要说明的是,假定式(13)的目的是能够解析地求解tgo和sgo,从而降低生成制导指令的计算量,而不是设计纵向升阻比c的剖面并跟踪该剖面,因此实际再入过程的c并不需要满足一次函数形式,这一点在许多预测校正制导方法中均有体现[11-13,17,20]。
2.3 飞行时间可控范围
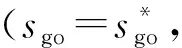

图1 飞行时间、飞行距离与纵向升阻比的关系Fig.1 Relationship between flight time, range and longitudinal lift drag ratio
对比文献[11]中的方法,假定c为常值,tgo和sgo的关系将退化为
(19)
以上分析表明,对于本文提出的制导方法,相较于将c视为常值,将c视为速度v的一次函数更为合理,后续仿真结果会对此作进一步说明。
3 时间协同再入制导
3.1 攻角指令
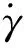
(20)
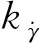
本文根据文献[22]中方法计算γQEGC,首先由式(11)对t求导,并假定dg/dt≈0,可得:
(21)
再将式(1)和式(4)代入式(21),同时假定sinγQEGC≈γQEGC, cosγQEGC≈1,整理可得:
(22)
式中:a1,a2和a3的具体表达式参见文献[22]。
参考攻角αplan直接影响飞行器在滑翔段的升阻比L/D,而剩余时间和剩余距离估计是基于纵向升阻比c进行的,因此αplan必须能够满足总飞行时间和飞行距离的要求,不能过小,同时也不宜过大,以免造成倾侧角过于频繁地反转。本文利用参考攻角αplan来满足对不同升阻比的需求,即在不同马赫数下维持某一升阻比(如果当前马赫数无法达到目标升阻比就用最大升阻比代替),如图2所示。
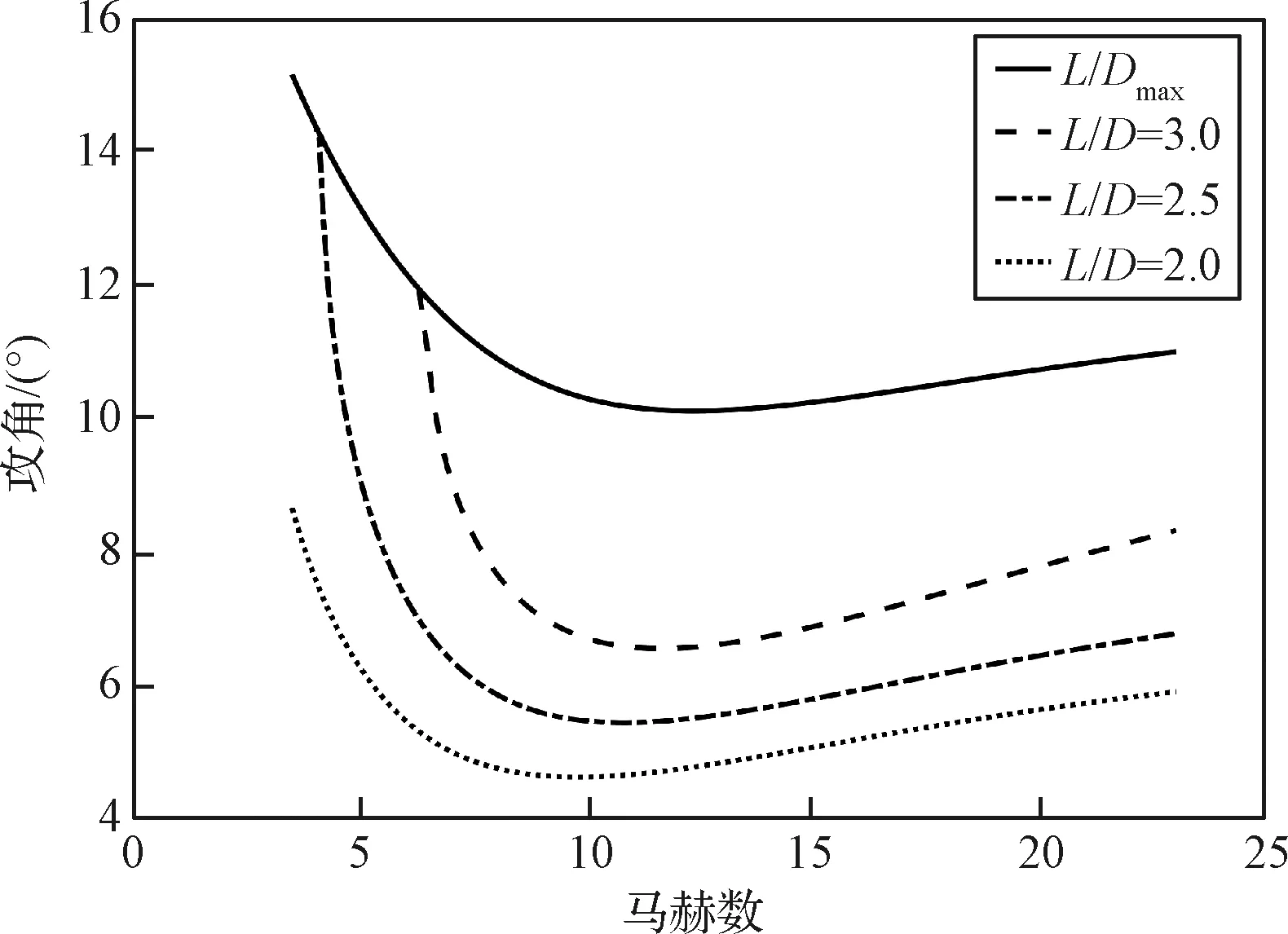
图2 不同升阻比下的攻角剖面Fig.2 Profiles of the angle of attack under different lift-drag ratios
3.2 倾侧角指令
下降段和转换段的主要目的是使飞行器尽快进入准平衡滑翔段,然后通过剩余时间和剩余距离进行预测校正制导并生成倾侧角指令,因此在下降段和转换段令倾侧角σ=0°。
3.2.1倾侧角幅值
(23)
在每个制导周期内,根据剩余时间和剩余距离估计式(14)和式(18)进行校正,则有:
(24)
式(24)是关于k0和k1的二元非线性方程组,可以利用牛顿迭代法快速求解。但由于式(15)的假设,或者再入过程中不确定性因素的影响,方程组式(24)可能得不到满足精度要求的解。此时,将求解k0和k1转化为参数优化问题,设目标函数为:
(25)
式中:tscale和sscale分别为时间误差和距离误差的归一化参数。利用参数优化的牛顿迭代法同样可以快速求解出使目标函数J最小的k0和k1。
得到k0和k1后,根据式(13)可求出当前制导周期内需要的纵向升阻比cplan。注意到式(14)和式(18)共同描述了剩余时间、剩余距离和末速度三者之间的关系,而终端约束式(9)中还包括对终端高度的约束。因此,纵向升阻比指令ccmd在cplan的基础上加入高度反馈项,以满足终端高度约束:
(26)
式中:uh为高度反馈项;kh为相应的系数。飞行器实际的升阻比L/D是可以测得的,那么倾侧角幅值大小|σ|为
(27)
如果ccmd>L/D,那么令|σ|=0。
3.2.2倾侧角幅值约束
为满足再入飞行的过程约束式(10),可以对倾侧角指令进行限幅,将式(10)中的过程约束转换为高度-速度约束,即再入飞行走廊的下限hmin(v)[23]:
(28)
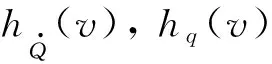
为满足过程约束限制倾侧角的大小,以避免飞行器因倾侧角过大而无法将高度维持在高度下限hmin(v)以上。最大倾侧角可以表示为[24]
(29)
式中:LQ为维持准平衡滑翔条件所需的纵向升力分量;Lmax为飞行器在式(28)约束下的最大升力;ε为反馈项;kσ为相应的系数;dh/dv为飞行器实际的高度变化率,dhmin/dv可通过式(28)得到。
综上,为满足过程约束,应当有:
(30)
3.2.3倾侧角符号
本文通过常见的倾侧角反转策略来控制飞行器的横向运动,以航向角误差走廊来确定倾侧角符号,即航向角误差超过设定值时改变倾侧角符号使其重新回到走廊内,反之则保持倾侧角符号不变。
设飞行器当前位置相对目标点的视线角为ψlos,定义视线角误差Δψ=ψ-ψlos,并将误差走廊Δψc设为关于速度v的分段函数:
(31)
式中:Δψ0, Δψ1和Δψf分别为v0,v1和vf时的误差走廊门限;v0和v1分别为初始速度和航向角误差走廊分段点的速度。
3.3 多飞行器协同策略
对于绝对时间协同再入,需要在发射前确定再入飞行时间tf,并使各飞行器在ti=tf时到达指定目标位置。根据滑翔段的初始条件,以剩余距离估计式(18)为约束,以剩余时间估计式(14)为目标函数,可求得各飞行器飞行时间可控范围Ti的估计。为保证协同再入时间tf存在,需要各飞行器的时间调节范围有交集。对于准平衡滑翔飞行,纵向再入轨迹比较平直,无法通过飞行高度的起落来改变飞行时间,时间调节能力比较有限。这也导致总飞行时间与总飞行距离存在较强的比例关系,为保证飞行时间有交集,应使各飞行器的飞行距离大致相当。对于高超声速滑翔飞行器,再入段的初始条件是由助推段的终端状态决定的。因此,可以通过助推段的方案设计来保证各飞行器再入段总飞行距离大致相当,从而确保协同再入制导的可行性。
4 仿真校验
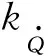
4.1 标称条件下的协同再入
针对高超声速滑翔飞行器协同再入,设计4个初始条件不同的再入任务进行仿真,具体参数如表1所示。根据协同再入策略,首先计算得到各飞行器的飞行时间可控范围估计分别为T1=1 396~1 632 s,T2=1 336~1 583 s,T3=1 345~1 592 s,T4=1 405~1 636 s。根据各飞行器的时间可控范围,将协同再入时间tf选为1 550 s,并以任务1为例,分别给出tf,1=tmin,tf,1=tf和tf,1=tmax时的仿真结果,如图3~4(a)所示。为对比本文方法与现有方法的不同,图4(b)给出了任务1利用文献[11]中方法时的仿真结果。对于任务1到任务4的协同再入,以协同飞行时间t=1 550 s为仿真截至条件并计算终端误差,结果如图5~10和表2所示。

表1 再入任务初始条件Table 1 Initial conditions in reentry missions
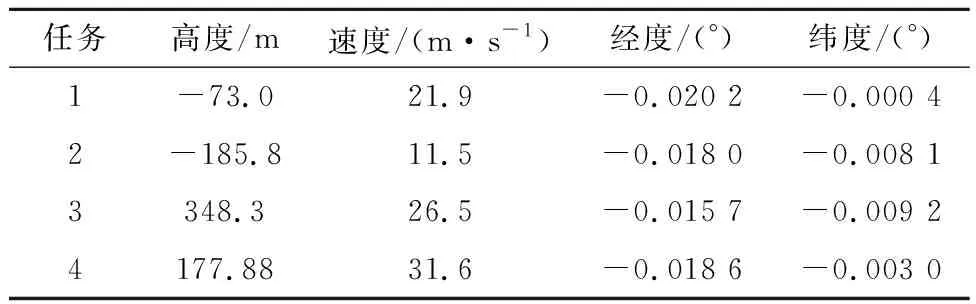
表2 标称条件下的终端误差Table 2 Terminal errors at nominal conditions
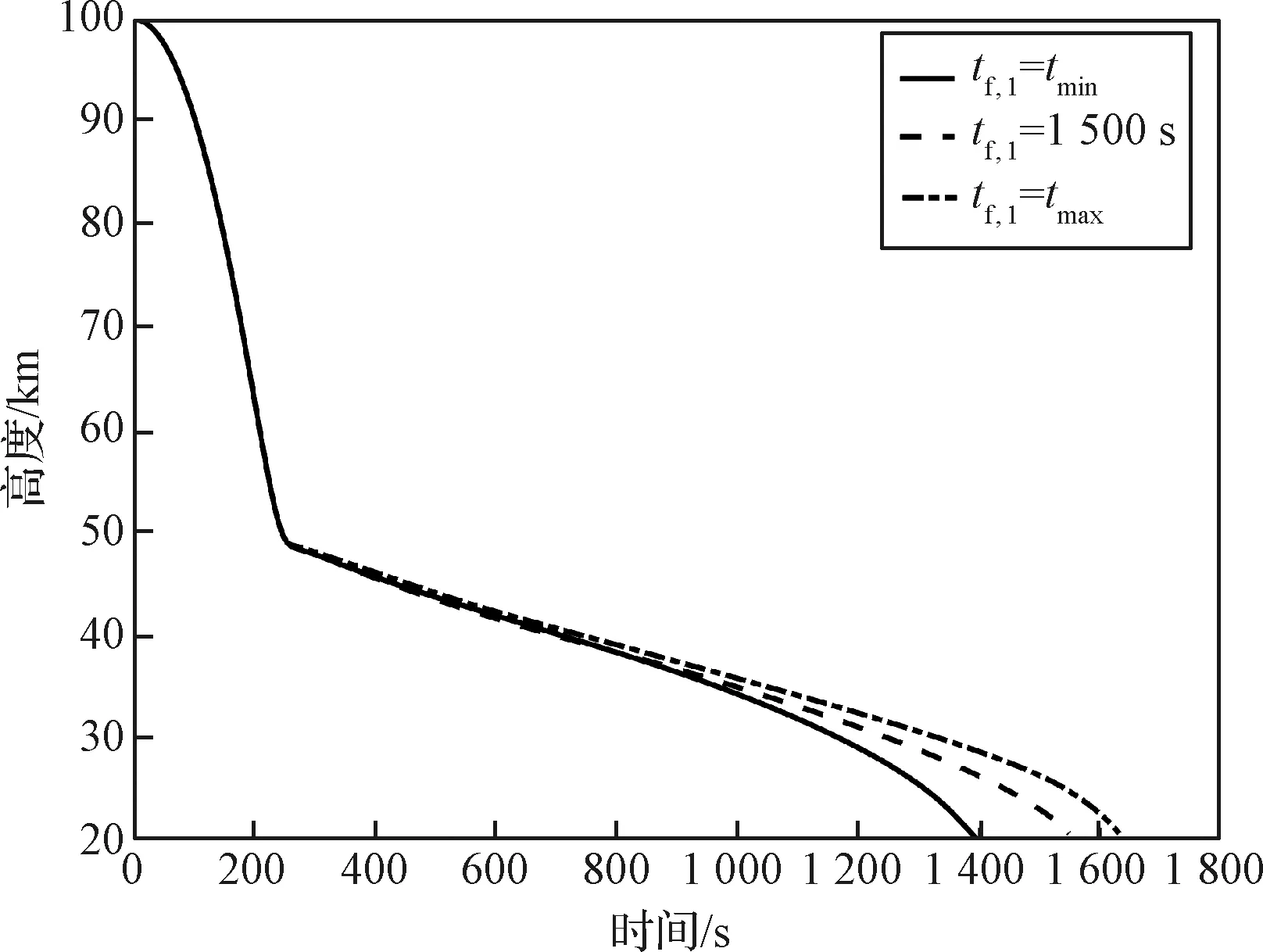
图3 不同时间约束下的高度-时间曲线Fig.3 Curves of altitude versus time under different time constraints

图4 不同时间约束下的速度-时间曲线Fig.4 Curves of speed versus time under different time constraints
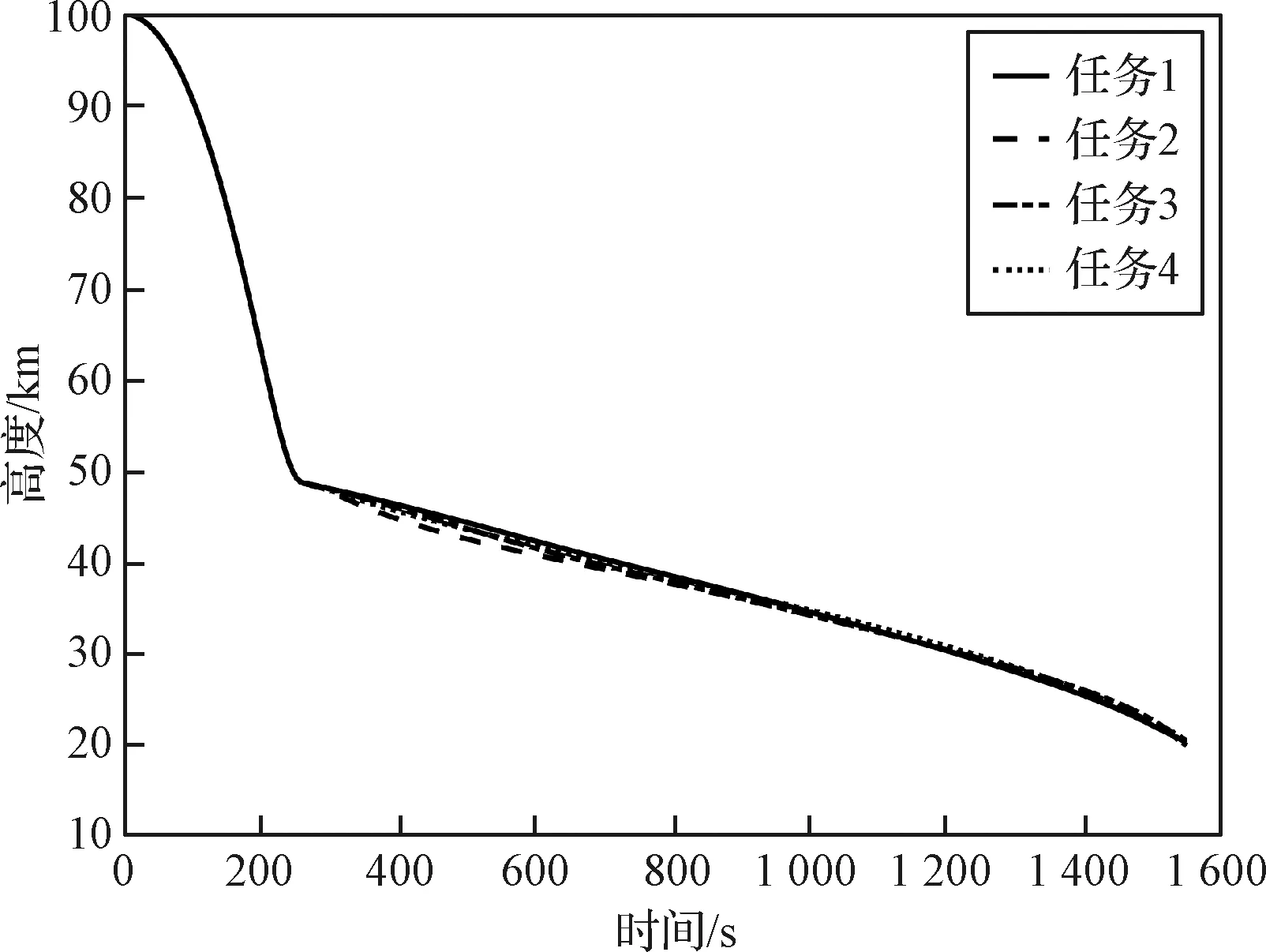
图5 标称条件下的高度-时间曲线Fig.5 Curves of altitude versus time under nominal conditions
对于本文方法,图3和图4(a)分别为不同时间约束下的高度-时间曲线和速度-时间曲线,可以看出终端高度约束和终端速度约束都较好地得到了满足。从图4(a)可以看出,随着总飞行时间的减少,速度-时间曲线的曲率随之增大。由于速度变化大小一致而变化时间不同,总飞行时间较短就需要速度先缓慢降低再快速降低,从而同时满足飞行距离和高度的约束,这与客观实际是相符的。对于文献[11]中方法,从图4(b)可以看出,在不同飞行时间约束下,速度随时间变化的趋势基本一致。飞行时间1 530 s和1 570 s对应的终端速度分别为2 253 m/s和1 664 m/s,与期望的终端速度分别相差253 m/s和336 m/s。对比以上结果可知,文献[11]中方法的时间可控范围为40 s,大约占总飞行时间的2%,并且需要放宽终端速度约束,而本文制导方法可将时间可控范围提高到236 s,大约占总飞行时间的14.5%~17%,并且能够更严格地满足终端速度约束。这说明将纵向升阻比c作为变量推导出的剩余时间、剩余距离和终端速度的关系更符合制导需求,以此设计的再入制导方法能更有效地发挥出飞行器的飞行能力。
表2为各再入任务的终端误差,可以看出本文提出的协同再入制导方法能够在满足时间约束的基础上,使终端高度、速度和经纬度的误差均保持在较小范围内,很好地实现了多飞行器协同再入,并能够为末制导提供良好的交班条件。图5和图6分别为协同再入的高度-时间曲线和速度-时间曲线,可以看出不同任务的高度和速度均较好地满足了其终端约束。图7为各再入任务的地面航迹,说明本文方法对不同初始条件均有较强的适应能力。相较于文献[14]中再入任务初始经纬度相差0.2°以内,本文方法能够实现总飞行距离相差700 km的不同再入任务的协同制导,再次体现将c作为设计变量的合理性。图8为标称条件下的控制量曲线,可以看出攻角和倾侧角指令无明显振荡。图9为标称条件下的航迹角曲线,可以看出飞行器能够快速进入并维持准平衡滑翔状态。图10为标称条件下的过程约束曲线,可以看出各再入轨迹均满足过程约束。

图6 标称条件下的速度-时间曲线Fig.6 Curves of speed versus time under nominal conditions

图7 标称条件下的地面航迹Fig.7 Ground tracks under nominal conditions

图8 标称条件下的控制量曲线Fig.8 Curves of controlled variables under nominal conditions
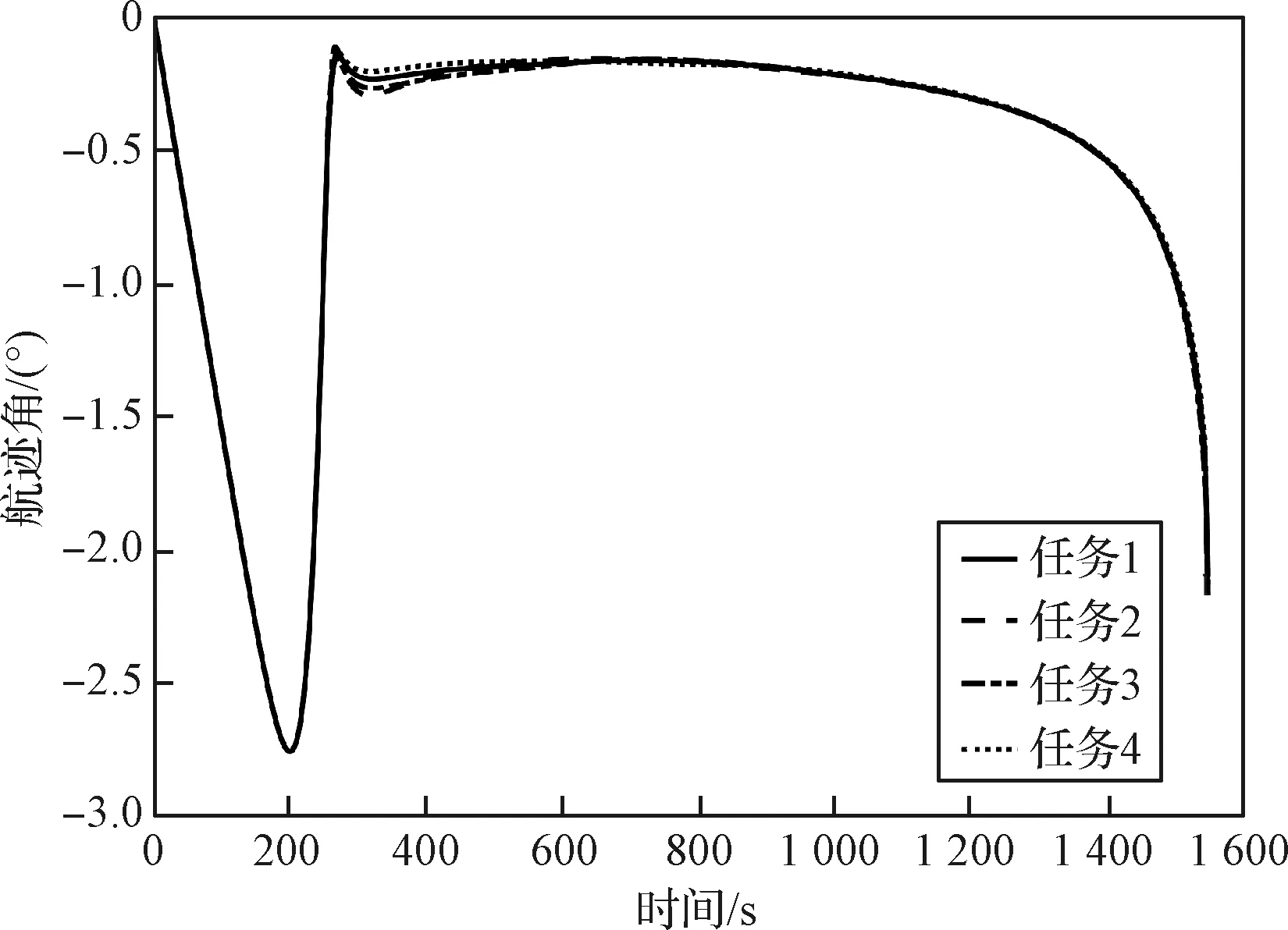
图9 标称条件下的航迹角-时间曲线Fig.9 Curves of flight path angle versus time under nominal conditions
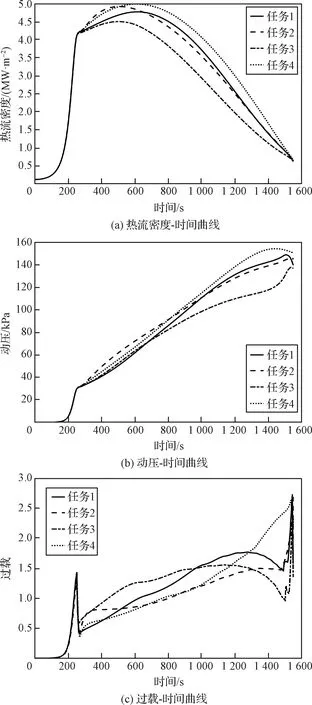
图10 标称条件下的过程约束Fig.10 Path constraints under nominal conditions
4.2 不确定条件下的协同再入
为验证本文制导方法在不确定条件下的可靠性,考虑大气密度ρ、升力系数CL、阻力系数CD和质量m存在偏差,进行500次的蒙特卡洛仿真。假设各参数偏差均符合正态分布,质量的偏差限为±5%,其余参数的偏差限为±10%。
图11为不确定条件下的终端高度-速度误差散布图,对于不同再入任务,可以看出终端高度误差大致在±4 km以内,终端速度误差大致在±100 m/s以内。图12为不确定条件下的终端经度-纬度误差散布图,对于不同再入任务,可以看出终端位置误差基本在10 km以内。以上结果表明本文制导方法在参数偏差条件下具有较好的精度和鲁棒性,能够满足协同再入制导的需求。
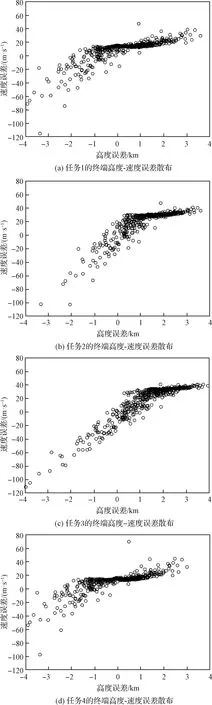
图11 不确定条件下的终端高度-速度误差散布Fig.11 Dispersions of terminal height error versus velocity error under uncertain conditions
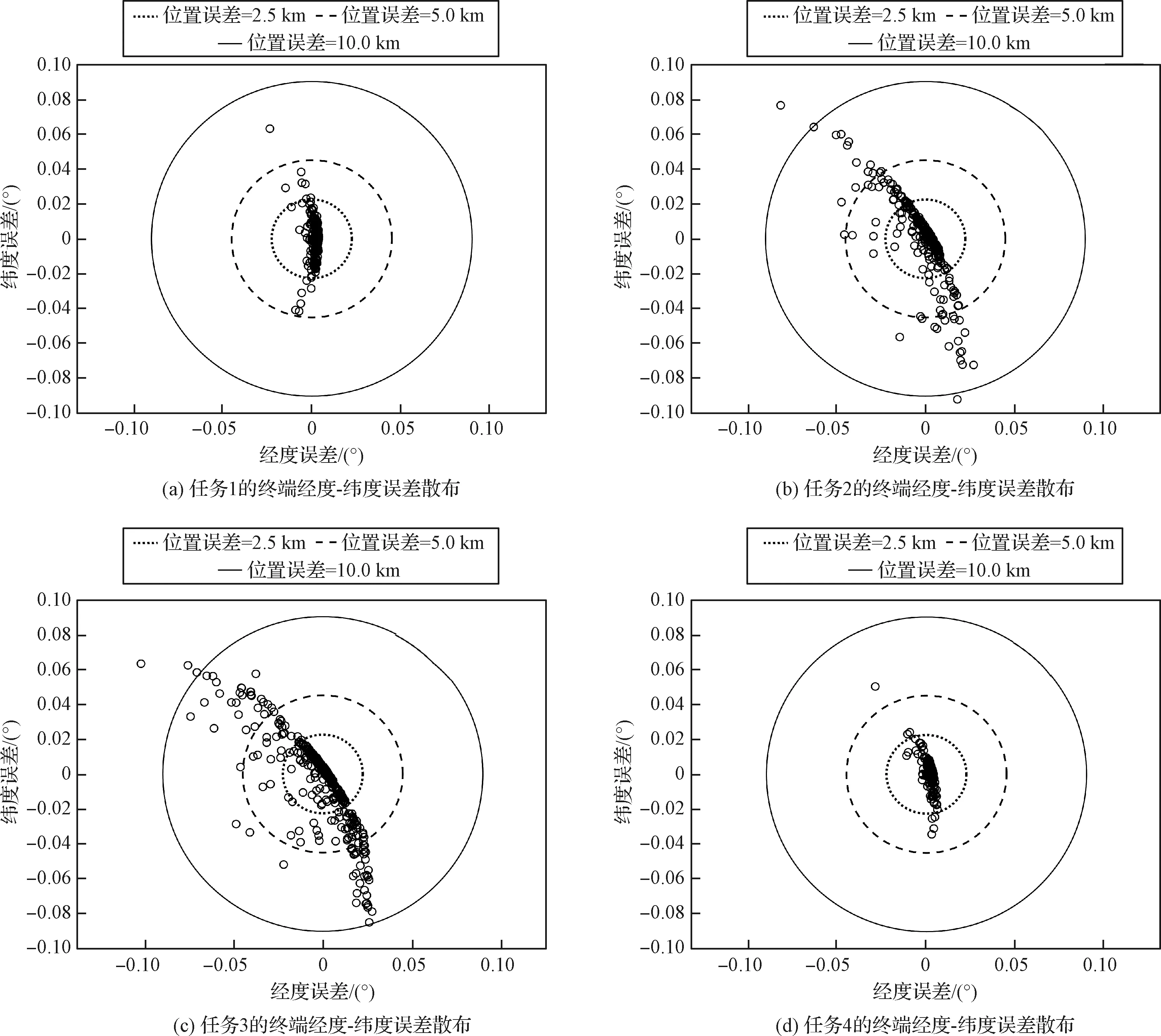
图12 不确定条件下的终端经度-纬度误差散布Fig.12 Dispersions of terminal longitude error versus latitude error under uncertain conditions
5 结 论
针对多高超声速滑翔飞行器协同再入制导问题,本文提出一种基于剩余时间估计和剩余距离估计解析解的协同再入制导方法。通过攻角指令设计使飞行器快速进入并保持准平衡滑翔,从而确保剩余时间和剩余距离估计的准确性。将纵向升阻比作为设计量预测校正剩余时间和剩余距离并生成相应的倾侧角指令,结合协同策略,实现了不同飞行时间和飞行距离的多飞行器协同再入。标称条件和不确定条件下的仿真结果表明,相比于将纵向升阻比视为常值的制导方法,本文方法能够大幅提高协同时间范围,并满足终端状态约束和过程约束,且在不确定条件下具有足够的精度和鲁棒性。

