海域和陆域地震动输入能量与强度指标相关性
胡进军,田 浩,谭景阳,刘巴黎,靳超越
(1.中国地震局工程力学研究所,哈尔滨 150080;2.中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080)

输入能量数值大小主要受强度指标、阻尼比等因素影响。Ganjavi等[11]发现EI/M、Ia、Vca、Id等强度指标对输入能量的影响存在显著差异,并提出了一种最优的无量纲强度指标(NE)作为归一化能量指标;Benevento等[12]分析了西班牙48次地震,发现VD/VE能够较好地评估地震动输入能量对结构破坏的影响;Fajfar等[13]提出了3个无量纲参数(R、γ、EH/EI)用于简化能量方法分析过程,并认为在实际设计过程中对能量谱进行适当简化不会影响设计准确性;王德才等[14]基于中国场地分类,分析了输入能量与12个强度指标在各周期段的相关性,发现与输入能量相关性最好的强度指标是Ie,并提出了新强度指标Te,该指标能够较好地体现震级、距离等因素对地面运动的影响。

随着海洋开发战略的发展,近海工程的兴建,这就对海域工程结构抗震设防提出了更高要求。而海域和陆域地震动特征存在差异,主要表现在幅值、频谱等特征。就幅值而言,海域和陆域地震动的Apg无较大差异,而海域地震动的Vpg值较陆域大[20];就反应谱而言,当周期小于0.5 s时,海域和陆域地震动的差异较小,但当周期大于0.5 s时,海域地震动的反应谱较大[21]。此外,同陆域地震动相比,海域地震动含有丰富的长周期成分[22]。随着基于性态的抗震设计的发展[23],研究海域地震动输入能量谱能够为近海域地区的海域结构的基于性态的抗震设防提供参考。概率地震危险性分析(PSHA)是基于性态的抗震设计中重要的一环,为给陆域PSHA提供参考,Cheng等[24-25]先后研究了基于地质统计工具的输入能量空间互相关模型和输入能量与强度指标的经验相关性。目前对输入能量谱的研究主要集中于陆域地震动,针对海域地震动输入能量以及海陆震动的输入能量谱差异的相关研究较少。为给海域PSHA研究提供参考,基于271次地震的6 264条海陆地震动记录,通过相关性分析的方法,从强度指标和阻尼比两个角度进行研究,并对比了海陆的相对与绝对输入能量和强度指标的相关性。
1 海域和陆域地震动数据
海域和陆域地震动数据选自日本K-NET台网,包括陆域台站和相模湾海域6个海底台站(ETMC)。共选取了271次地震事件,其中海底台站记录到的地震事件为264次,陆域台站记录到的地震事件为213次,海陆共同记录到的206次,共计3 132组双向水平地震动数据,其中海域地震动数据892组,陆域地震动数据2 240组。海陆台站的位置及地震震中位置见图1。

图1 海陆台站及地震震中
由于震中距会影响相关性,因此需对地震动记录按照距离分组,在每组数据尽可能平均的前提下将海陆的地震动记录按震中距分为3组:0~60 km、60~100 km、100~300 km,矩震级(Mw)与震中距关系见图2。在使用K-NET数据研究前,需处理数据,首先进行基线校正使地震动记录回归零基线位置;然后通过滤波去除地震动记录的高频和低频“噪声”。采用Boore等[26-27]提出的基线校正方法,将加速度、速度和位移分别处理。由于峰值位移(Dpg)等位移类强度指标对基线校正较敏感,为保证数据主要信息不丢失以及防止地震动位移时程失真,对加速度记录采用4阶Butterworth非因果滤波器进行滤波,选用带通滤波器,截止频率为0.05~25.00 Hz,并对加速度记录事件前后补零,用足够长的零扩展记录,在所有分析中保留这些零填充部分可避免兼容性问题,且后续不需要进一步校正[28-29]。

图2 海陆震动记录震级与震中距关系
2 单自由度体系弹性输入能量计算方法
由于坐标系选取不同,单自由度体系在水平地震动作用下存在两种形式的运动方程[6],在绝对坐标系下的运动形式见图3(a),其运动方程为
(1)

根据其运动方程,可推导出弹性输入能量表达式,在绝对坐标系下弹性输入能量(以下简称绝对输入能量)的计算公式为
(2)
在相对坐标系下,单自由度体系的运动形式见图3(b),其运动方程为
(3)
在相对坐标系下的弹性输入能量(以下简称相对输入能量)的计算公式为
(4)
为消除结构质量影响,在地震动输入能量研究中,通常用其等效速度代替输入能量[6],其公式为:
(5)
(6)

图3 水平地震动作用下单自由度体系运动模型
3 强度指标的选取
3.1 常用的强度指标
多种强度指标曾被定义来表征地震动强度,由于地震动和结构的复杂性,一些研究根据不同的研究对象选择强度指标,但没有明确的单一强度指标可以完整地表征地震动破坏势[30]。地震动对结构的破坏能力主要与地震动的持时、幅值以及频谱有关[31]。因此为选取代表性强度指标,筛选了20个常用的强度指标,涵盖了地震动三要素:幅值、持时以及频谱,见表1,表中T为单自由度体系的自振周期。括号持时是指地震动首末两次达到所规定的阈值所经历的总时间,考虑到海域地震动记录的峰值加速度较小,因此将括号持时的阈值设为5 cm·s-2。
3.2 强度指标的相关性分析
通过计算不同强度指标之间的Pearson相关系数,来确定代表性的强度指标。基于所选地震动记录计算了强度指标间的相关性,结果见表2,根据强度指标间的相关性,同时综合考虑幅值、持时、频谱,最终选取7个强度指标,分别是:Vpg、Db、Vmi、Vca、Sv0.2、Sd1.0、Ia。以Vca与Sd1.0、Vpg与Ia为例绘制散点图,从图4的拟合效果可看出两对强度指标有较好相关性,图中R为Pearson相关系数。

表1 常用的强度指标
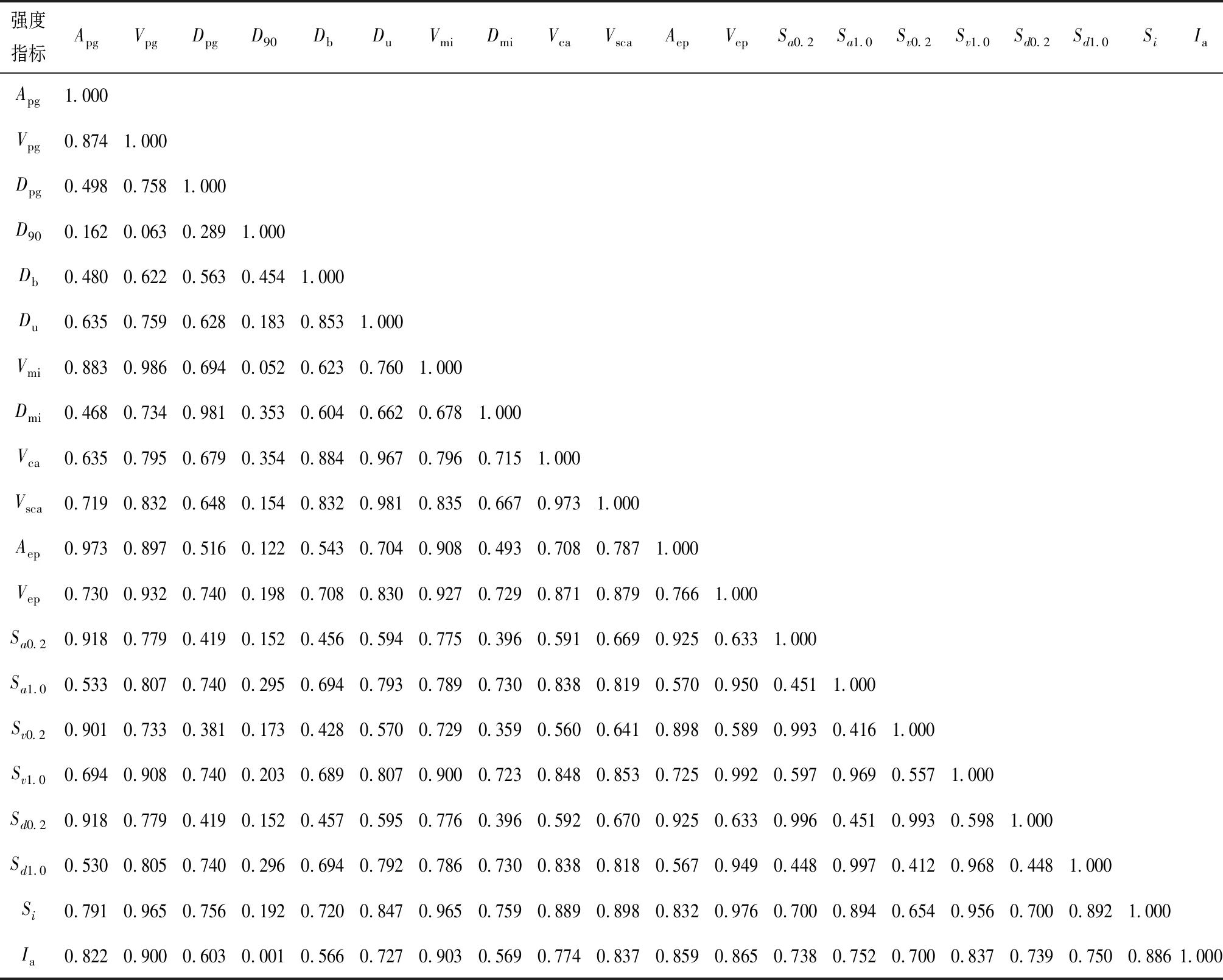
表2 初步筛选的20个强度指标间的相关系数(绝对值)

图4 两对强度指标的线性拟合关系
4 输入能量与地震动强度指标的相关性
基于上述7个强度指标,为全面解释其与地震动输入能量之间的关系,根据不同震中距和阻尼比分组计算了所选地震动在不同工况下的绝对和相对输入能量(Ea和Er),并分析了其与强度指标的相关性及其海陆差异。由于不同自振周期的结构对强度指标敏感程度不同,且所选7个强度指标并非在所有周期段与输入能量相关性规律都相同,因此需进行周期段划分。翟长海[32]将单自由度体系的自振周期(T)划分为3个周期段:当T≤ 0.5 s 时为短周期;当0.5 s
4.1 不同距离下输入能量与强度指标的相关性分析
由于近场和远场地震动特征存在很大差异,因此基于震中距分组,分别计算了所选海域与陆域地震动阻尼比为0.05时的Ea和Er,并将其结果与所选强度指标进行相关性分析。在不同震中距下,研究了海域与陆域地震动的不同强度指标与输入能量的相关性。由于Pearson相关系数易受到极端值的影响,基于震中距分组的数据量较少,因此本节选用Spearman相关系数,其计算公式为
(7)
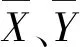
图5为不同震中距下的海域与陆域地震动Ea与不同强度指标的相关系数。在不同周期段,与海域和陆域地震动Ea相关性最好的强度指标存在微小差异,具体表现在相关系数的数值上。在短周期范围内,与海域和陆域地震动Ea相关程度最好的强度指标都是Ia,这与叶列平等[31]的研究成果一致,叶列平等[31]发现以Apg为代表的第一类强度指标在短周期范围内,与单自由度体系在地震作用下的响应相关程度较高,Ia为该类强度指标。而在中长周期范围内,与海域和陆域地震动Ea相关性最好的强度指标都是Sd1.0,随着自振周期的增大,Sd1.0与其相关性呈现先上升后下降趋势,在T=1.0 s时达到最大,由此可见在中长周期范围内Ea与Sd1.0有较好相关性,这一结论与谭景阳等[33]的研究结果相似,谭景阳等[33]发现Dpg与海域长周期结构在地震作用下的响应相关性最好,根据叶列平等[31]的定义,Sd1.0与Dpg同为第三类强度指标。
对比图5(a)、(c)、(e)和图5(b)、(d)、(f)可发现,海域和陆域地震动Ea与7个强度指标在不同震中距情况下的相关性呈现4种结果:1)Sd1.0与海域和陆域地震动Ea的相关性在3个震中距情况下所呈现的趋势一致,即相关性先上升后下降,当周期约为1.0 s时,达到最大;2)Vca与海域地震动Ea的相关性趋势在各震中距条件下一致,即在短周期范围内上升,在中长周期范围内保持相对稳定,而Vca与陆域地震动Ea在0~60 km、60~100 km震中距情况下的相关系数存在1个极大值和1个极小值,极大值出现在0.3 s附近,极小值出现在1.0 s附近,而其在100~300 km震中距情况下只有1个极小值;3)Db与海域地震动Ea的相关性在0~60 km情况下先升高后趋于稳定,在60~100 km、100~300 km的情况下,Db与海域地震动Ea的相关系数存在两个极值,1个极大值1个极小值,而陆域地震动Ea与Db的相关性在各震中距范围下,均存在两个极值,即1个极大值和1个极小值;4)Vpg、Vmi、Sv0.2、Ia与海域和陆域地震动相关程度均随着震中距的增加而降低且都只有1个极小值,所不同的是,海域地震动Ea与上述4个强度指标相关系数的极值出现在1.0 s后,海域地震动Ea与其相关系数的极值出现在1.0 s前。

图5 海陆强度指标与Ea的相关系数
图6为不同震中距下的海域和陆域地震动Er与不同强度指标的相关系数。Sv0.2在T=0.2 s时相关程度高于其他强度指标,但其相关系数值迅速下降。在短周期范围内,与海域和陆域Er相关性最好且较为稳定的强度指标仍是Ia;在中周期范围内,与海域和陆域Er相关性最好的是Sd1.0,相关解释已在4.1.1节中描述;在长周期范围内,Sd1.0与海域和陆域Er的相关性呈现下降趋势,但Vpg、Vmi与海域和陆域Er的相关性呈现上升趋势,最终相关系数值大于Sd1.0。不同周期段差异与Uang等[6]在关于Ea与Er在不同周期段的差异的研究结果一致。
对比图6(a)、(c)、(e)和图6(b)、(d)、(f)可发现,海域和陆域地震动Er与7个强度指标在不同震中距相关性结论与Ea基本一致。因此,震中距会影响地震动Er与强度指标的相关程度,具体体现在影响相关系数大小、极值个数以及造成海陆差异。海域和陆域的Ea、Er在不同震中距以及不同周期段与其他强度指标的相关性情况见表3。

表3 不同工况下与地震动输入能量相关性最好的强度指标
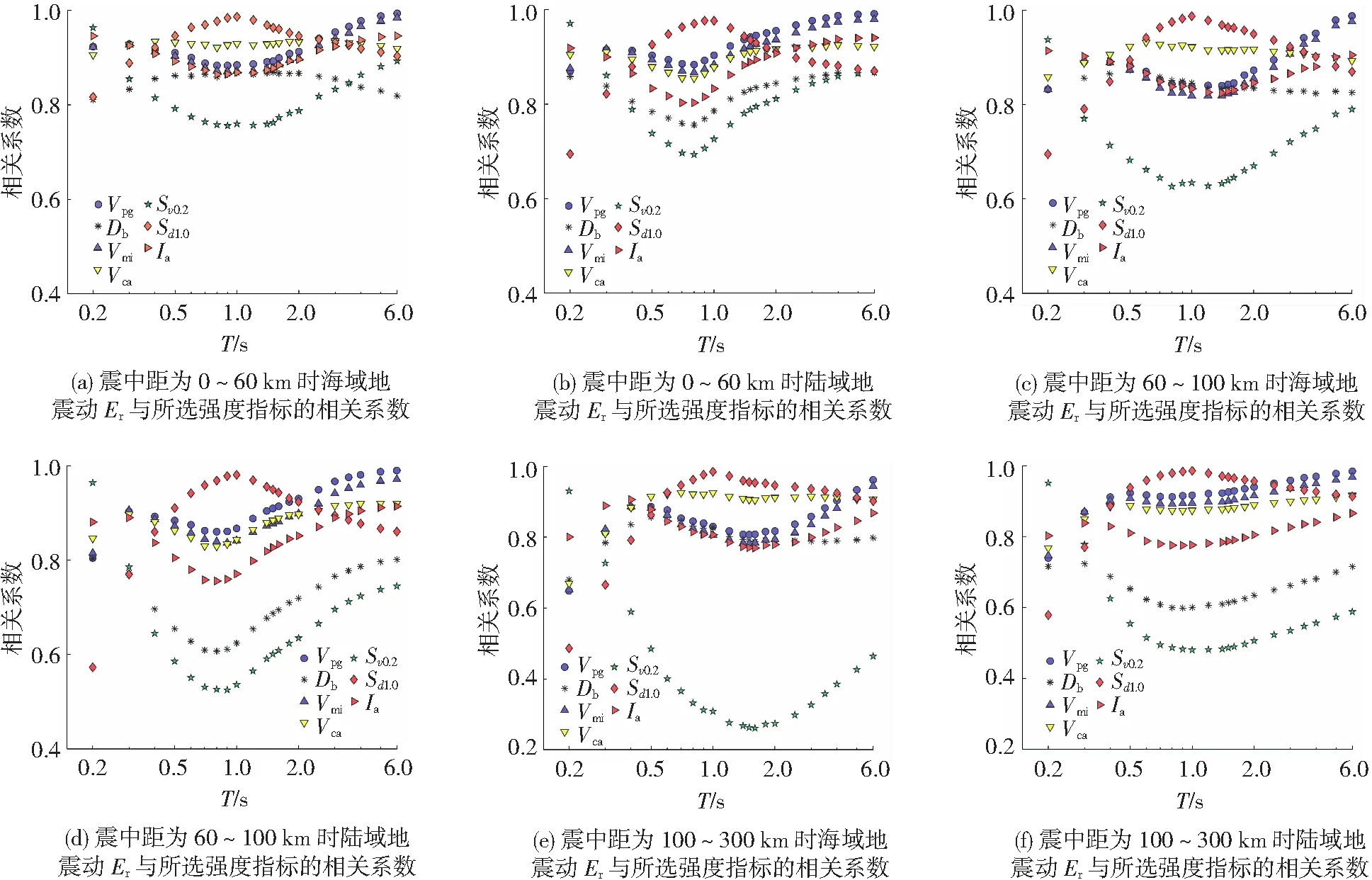
图6 海陆强度指标与Er的相关系数
4.2 不同阻尼比下输入能量与强度指标的相关性
在研究阻尼比对海域和陆域地震动Ea和Er与强度指标相关性的影响时,分别分析了第3节所筛选的7个强度指标在不同阻尼比下与Ea和Er的相关性。海陆震动Ea与在不同阻尼比下与所选7个强度指标的相关性见图7~9,由于结论类似,以图7所示海域和陆域地震动记录的Ea在不同阻尼比下与Ia的相关性为例对这一结论加以说明。图7(a)、(b)分别为海陆地震动记录的Ea与Ia的相关系数,对比两图结果可知,海陆地震动Ea与Ia在全周期的相关性程度均随着阻尼比的增大而增大,且随着自振周期T的增大而趋于稳定。
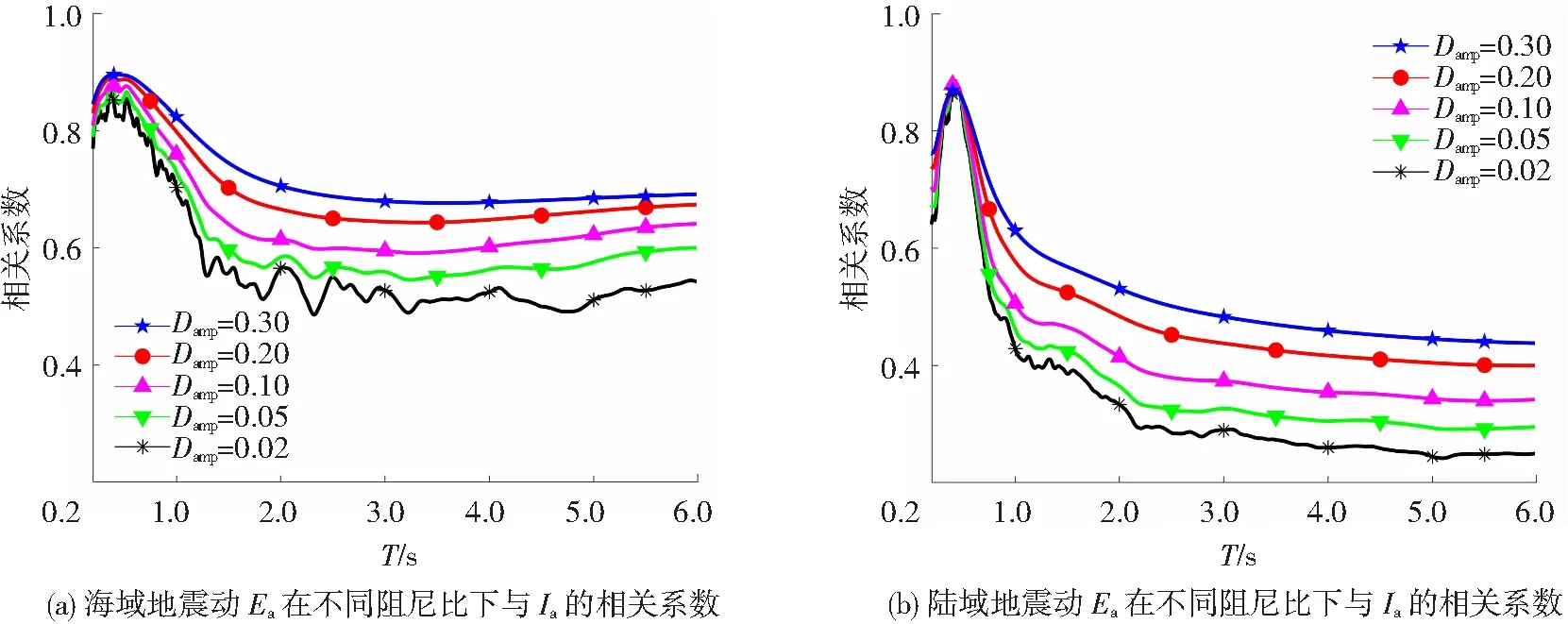
图7 海陆地震动Ea在不同阻尼比下与Ia的相关系数
在研究海域和陆域地震动Er在不同阻尼比下与所选强度指标的相关性时,有两种情况:1) 有3个强度指标的分析结果与Ea对应结论相同,即Vca、Db、Sd1.0,海域和陆域地震动Er与Vca、Db、Sd1.0在全周期段相关性均随着阻尼比的增大而增大且其值随着自振周期T的增大而趋于稳定,见图10~12;2)Ia、Vmi、Vpg、Sv0.2的结果却与上述情况不同,就陆域地震动Er而言,上述4个强度指标与Er在全周期的相关程度随着阻尼比的增大而增大,见图13(b)、图15;但海域地震动情况与陆域地震动不同,具体表现为:当自振周期T<4.0 s时,上述4个强度指标与海域地震动Er的相关程度随着阻尼比的增大而增大,当自振周期T>4.0 s时, 上述4个强度指标与海域地震动Er的相关程度随着阻尼比的增大而减小,见图13(a)、图14。
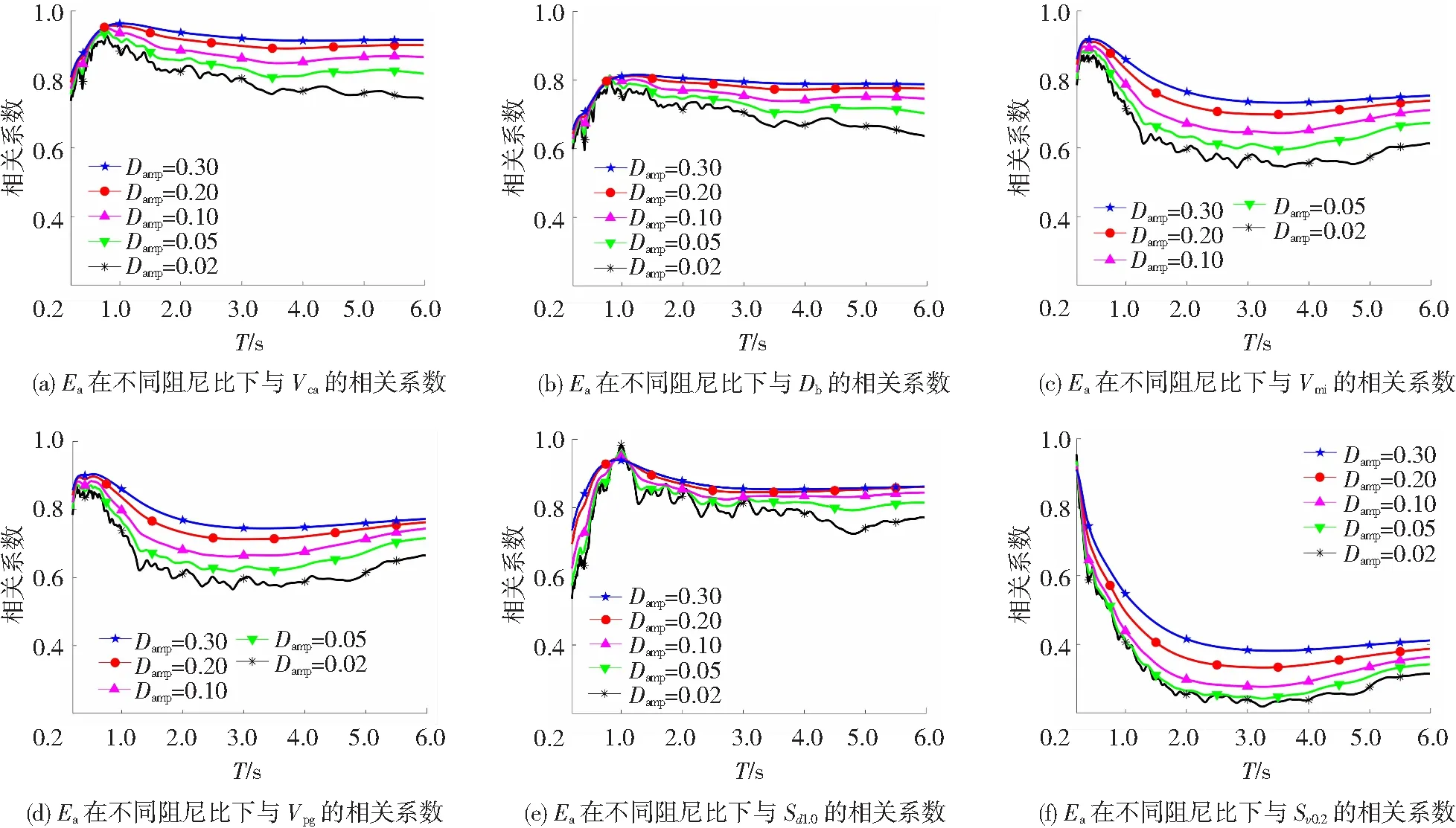
图8 海域地震动Ea在不同阻尼比下与其他强度指标的相关系数

图9 陆域地震动Ea在不同阻尼比下与其他强度指标的相关系数

图10 海陆地震动Er在不同阻尼比下与Vca的相关系数

图11 海域地震动Er在不同阻尼比下与其他强度指标的相关系数
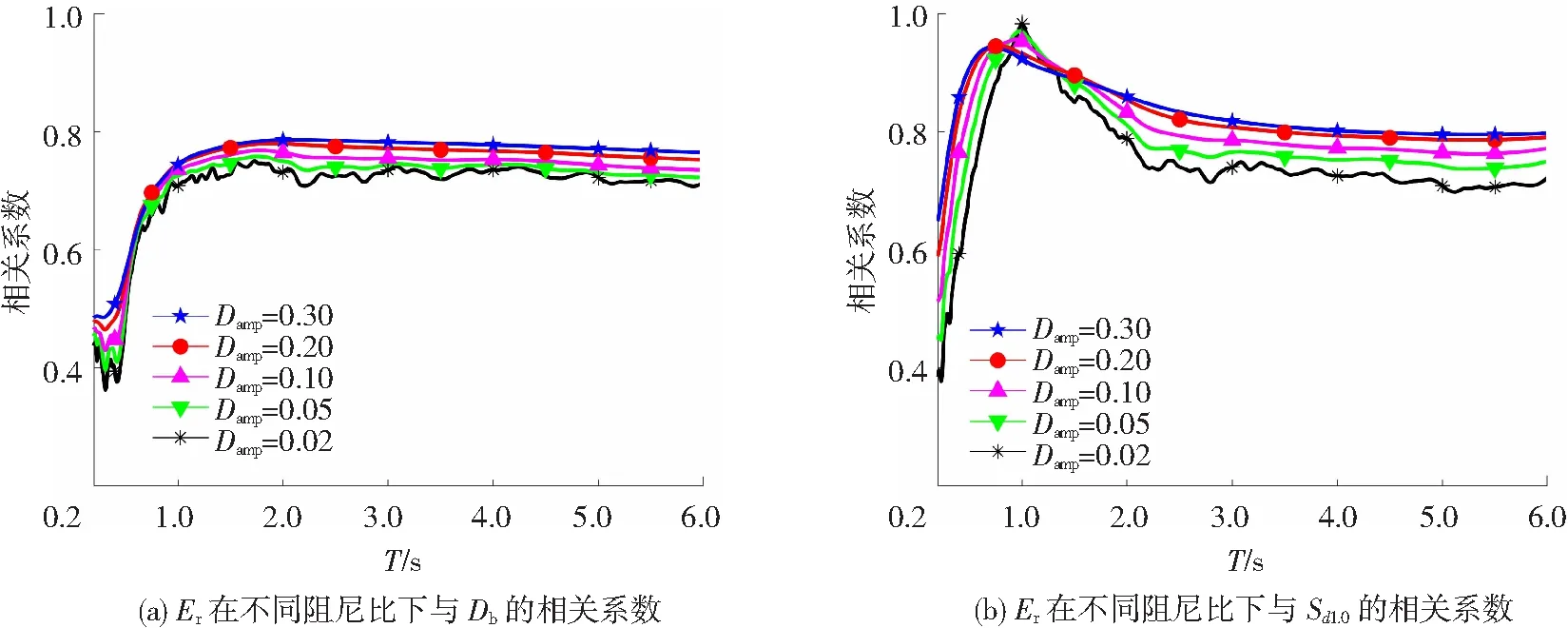
图12 陆域地震动Er在不同阻尼比下与其他强度指标的相关系数
海陆地震动的频率成分存在差异,可能是导致上述现象的原因。通过滤波去掉海域地震动记录的低频成分,将截止频率设置为1.0~25.0 Hz,再将海域地震动记录的Er与Ia、Vmi、Vpg、Sv0.2进行相关性分析,得到与陆域地震动相似的结果,即随着阻尼比的增加,上述4个强度指标与海域地震动记录Er的相关程度随着阻尼比增大而增大,结果见图16。说明:海域地震动记录低频成分的丰富可能影响了上述强度指标与Er的相关性规律。
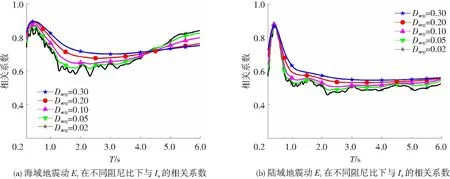
图13 海陆地震动Er在不同阻尼比下与Ia的相关系数

图14 海域地震动Er在不同阻尼比下与其他强度指标的相关系数
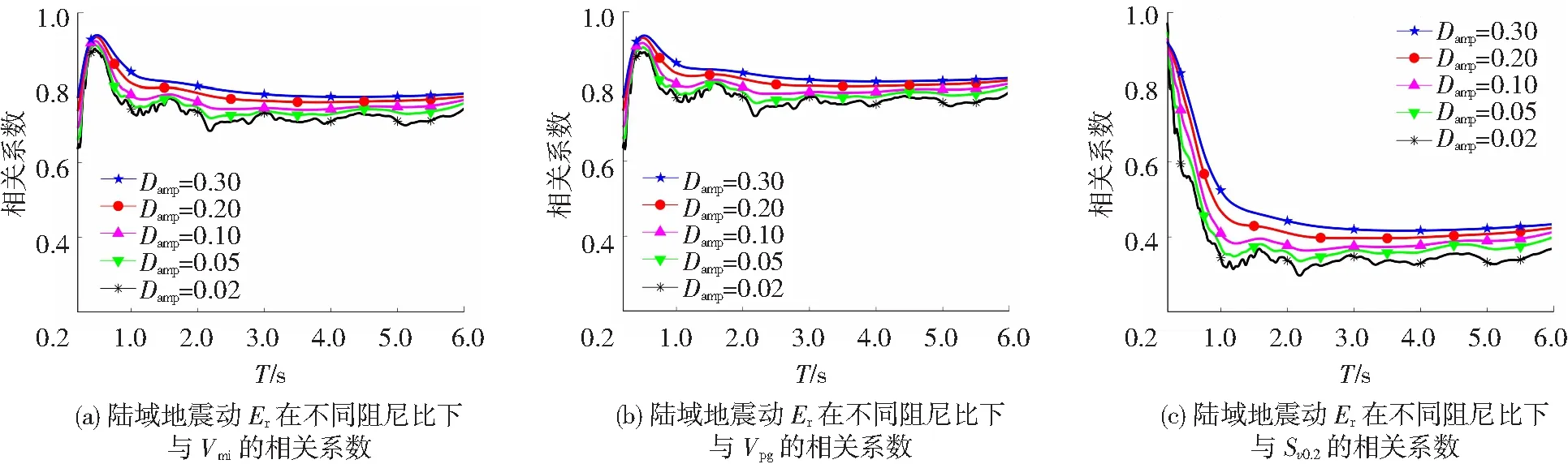
图15 陆域地震动Er在不同阻尼比下与其他强度指标的相关系数

图16 海域地震动Er在不同阻尼比下与强度指标的相关系数
5 结 论
考虑震中距和阻尼比,研究了海域与陆域地震动输入能量与其他强度指标的相关性,结果表明,海域和陆域地震动输入能量与强度指标的相关性存在异同,主要结论如下:
1)就不同周期段而言,与海域和陆域Ea相关性最好的强度指标基本一致,即在短周期范围内,与海域和陆域Ea相关性最好的强度指标是Ia,在中长周期范围内,与海域和陆域Ea相关性最好的强度指标Sd1.0;而海域和陆域的Er与所选强度指标的相关性与Ea在中长周期内存在差异,具体表现在Sv0.2、Vpg、Vmi上,在0.2 s时,Sv0.2与海域和陆域的Er相关性最好,Vpg、Vmi与海域和陆域的Er的相关程度在长周期范围内呈现上升趋势,相关系数最终大于Sd1.0。
2)从不同震中距范围来看,Ea与Er和所选强度指标的相关性趋势一致,但海域和陆域的输入能量与强度指标的相关性趋势存在差异,具体体现在海域和陆域与输入能量相关系数的数值大小、极值个数以及极值出现的周期点。
3)就不同阻尼比而言,所选强度指标与海域和陆域Ea的相关性趋势一致,即相关性程度均随阻尼比的增大而增大。但与Er相关性趋势存在较大差异,Ia、Vmi、Vpg、Sv0.2与陆域地震动Er相关程度在全周期的相关性程度均随阻尼比的增大而增大,但与海域地震动相关性出现不同情况:当T<4.0 s 时与海域地震动记录的Er相关程度随着阻尼比的增大而增大,但当T>4.0 s 时与海域地震动Er相关程度随着阻尼比的增大而减小。初步分析表明:造成此现象的原因可能是海域地震动低频成分较陆域地震动丰富。

