基于信号强度的地铁CBTC系统干扰源定位

魏诗燕，沙 泉，邹劲柏

（上海应用技术大学 轨道交通学院, 上海 201418）

随着国内列车运行控制技术的不断发展，基于通信的列车运行控制(communication based train control，CBTC)系统已经广泛应用于城市轨道交通中。国外的地铁CBTC系统运营体制不同于国内，列车内的信号多被屏蔽，地铁乘客量较小，因此列车出现受到信号干扰而逼停的情形很少。而且一些国家的CBTC系统为了预防乘客信息系统对其可能造成的影响，主要对列车内部的乘客信息系统引起的信号干扰进行屏蔽或优化，所以关于CBTC系统受到无线信号干扰方面的研究相对较少。而我国地铁允许列车内部乘客使用手机无线上网，中国移动、联通、电信等运营商为满足乘客不断增大的上网需求，均在城市轨道交通沿线部署了3G、4G等信号，使CBTC系统不可避免地受到了众多无线网络的干扰，降低了CBTC系统运行的安全性和稳定性[1-2]。为了提高地铁运行安全性和稳定性，对地铁CBTC系统抗干扰技术的研究已经成为迫切的需求。

国内外有一些学者研究了CBTC系统抗干扰的相关问题。文献[3]提到了CBTC系统内的无线干扰情况，该情况指1个地面无线接入点(access point,AP)对应了多辆列车同时与其通信。为解决地铁上多个用户尝试通过同频信道接入AP而产生的同频干扰问题，文献[4]通过引入载波侦听多址/冲突避免（the carrier sense multiple access/collision avoidance random access, CSMA/CA）的随机接入协议。目前国内外基于地铁干扰方面的研究大多在干扰类型的分类，以及对干扰环境进行测试，用不同的方法改进系统的信道选择和接入程序。然而，对于CBTC干扰源识别和定位方面的研究却很少。

为了准确地定位干扰源，首先要选择合适的定位算法。何平川等[5]提出了一种基于到达时间几何时差（time difference of arrival ，TDOA）的时差定位分析方法。王棋萍等[6]根据干扰信号的衰减效应，提出了一种分布式的基于干扰信号强度（received signal strength indicator, RSSI）估计的干扰源定位算法。与普通手机通信不同，列车是沿规定的轨道线路运行，其通信制式通信是线状网络。梯度下降和Taylor算法均可解决由于直线轨迹引起的非线性问题，文献[7]将这2种算法联合，梯度下降-Taylor展开多点联合定位优化算法的优点是可用更少的时间通过少数几步迭代就能收敛到目标。

本文首先提出了一种基于RSSI算法的地铁CBTC干扰源定位方案。该方案在优化算法方面，选用了拥有简单、易理解、参数较少等特点的粒子群算法[8-10]，使得定位的干扰源位置信息更精准。

1 研究模型

1.1 干扰源定位模型

本文的地铁研究环境设计为无其他障碍物，且假定干扰源在铁路沿线两侧的地铁线路。城市地铁呈线状分布，分为直线、圆曲线以及连接它们的三次抛物线缓和曲线。为了方便研究，本文主要选定直线轨道线路进行干扰源的定位研究[11]。如图1所示，（X1,Y1）是需要确定的目标干扰源位置。列车在运行过程中，因为在不同位置(xi,yi)距离干扰源距离不同，列车可以接收到来自同一干扰源不同强度的信号。

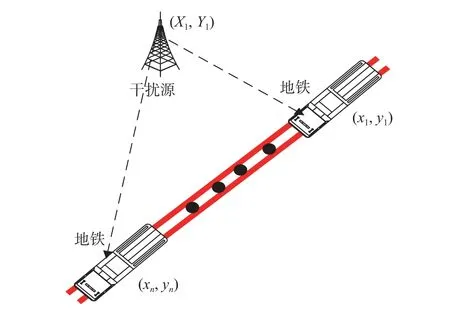
图1 干扰源定位模型Fig. 1 Interference source location model

所以通过收集列车在不同位置接收到来自干扰源不同的信号强度Si，可以计算出列车在某位置和干扰源的距离di，但是di并不能确定目标干扰源的位置坐标。为得到目标干扰源的位置，先假定一个干扰源位置(X0,Y0)。通过两点间的距离公式，可以得出列车在不同位置与假设干扰源(X0,Y0)的距离为：

式中，i=1,2,···,n表示列车运行过程中在不同位置接收到的第i个信号。再通过优化算法可对假定干扰源位置进行不断的修改，直至逼近目标干扰源（X1,Y1）。

1.2 RSSI测距模型

在很多的理论与实践中可以发现，信道的大尺度衰落特性是服从正态分布的[12-13]。即列车接收到的RSSI和列车与干扰源间的距离之间呈对数变化，当收发天线之间的距离为d时，信号的路径损耗表达式为：

式中：N表示路径损耗系数，由周围环境决定；P(d0)为参考距离d0的路径损耗值；Xσ是高斯随机变量，其平均值是0，其标准差是σ。

由此可以得到列车接收到干扰源的信号强度Si的表达式：

式中，参数A和N按照文献[7]给出的数值，其中A=-21.0742；N=2.451 8。此RSSI数据来源于不同速度的列车沿200 m直线轨迹运行时采集模拟干扰源的WIFI信号。

2 粒子群优化算法

2.1 初始位置和目标函数

通过设定干扰源初始位置(X0,Y0)，再根据列车在不同测试点的位置(xi,yi)，利用式（1）可得到测试点与设定的初始位置的距离为。

2.2 算法介绍

使用粒子群优化算法对初始位置(X0,Y0)进行修正，使得f取得极小值，得到目标干扰源位置。粒子群优化（particle swam optimization, PSO）是一种迭代随机搜索算法，算法是通过粒子间的相互作用而发现复杂搜索空间中的最优区域。在搜索空间中，每一个解都是1个单独的没有体积和质量的粒子，所有的粒子还具有1个速度参数来决定他们飞翔的方向和距离。然后粒子群会追随当前的最优粒子在解空间中搜索。在每次迭代中，粒子会根据2个极值信息来自我更新：①单个粒子自身经历过的最优解（position best，pb）；②所有粒子经历过的最优解（global best，gb）。用这种方法，粒子群可以逐渐逼近那个最合适的解，从而找到最终的最优解[14]。但是，粒子群算法容易陷入局部最优，从而导致最终结果不是最适合的解。为此，本文基于基础的粒子群算法进行了一些改进，使得最终结果跳出局部最优，得到全局最优解。

2.2.1 速度变异粒子群算法

为了避免搜索过程中陷入局部最优，可采用速度变异的改进粒子群算法[15-16]。基础的PSO算法描述如下：假设在1个D维目标搜索空间中，N个粒子组成1个粒子群，第j个粒子的位置和速度可分别表示为xj=(xj1,xj2,···,xjD)和vj=(vj1,vj2,···,vjD)。并且vj是根据自己以往最优的解pb和整个种群中最优的解gb进行动态调整。速度更新是通过粒子的当前速度和位置的线性组合来计算的。单独粒子的局部最优解的位置是pj=(pj1,pj2,···,pjD)；整个粒子群的全局最优解的位置是pg=(pg1,pg2,···,pgD)。每个粒子根据以下公式迭代更新速度和位置：

式中：j=1,2,···,n；d=1,2,···,D；c1和c2是学习因子，是为了增加粒子的多样性而加的扰动，c1为粒子个体的加速权重系数，c2为粒子群体的加速权重系数，粒子的最大速度限定为Vmax；r1和r2是随机数，服从（0，1）之间的均匀分布；是粒子j的当前速度；是粒子j的更新速度；是粒子j的当前位置；是粒子j的更新位置。式（5）决定了粒子的运动速度，由式（5）可见，第j个粒子的第（t+1）次迭代的运动速度由3个部分组成：第1部分代表了粒子自身的运动惯性，它的值是由前一次迭代的粒子运动速度所决定的；第2部分代表了粒子群个体对自身经历的认知，其作用在于吸引粒子向着自身经历过的最优方向运动；第3部分代表了粒子群对群体经历的认知，其作用在于使粒子群向全局最优方向运动。在更新过程中，粒子每一维的速度限制在[-Vmax，Vmax]内，粒子每一维的位置也被限制在允许范围之内。同时，个体极值和全局极值在迭代过程中不断更新，最后输出的全局极值就是算法寻优到的最优解。

为了避免粒子j在 搜索的后期因为运动速度为0而陷入局部最优，选取粒子j在每一维运动速度中的最小值，按照一定的概率进行变异，使原本聚集的粒子群分散开，脱离局部最优位置。令

为每一维的速度最小值，并把对应的粒子速度按照一定的概率重新设置初值。

则各粒子以速度vj根据式（6）运动到新的位置点。

2.2.2 结合自适应惯性权重的混合粒子群算法

ω是惯性加权系数，用来控制历史速度对当前速度的影响程度，一般在[0.1, 0.9]之间取值。为了避免粒子群算法陷入局部最优值情况的发生，对ω采取了一些改进方法，即使用自适应惯性权重并引入模拟退火算法的粒子群算法。改进后的粒子群算法将采用常见型ω转化为非线性惯性权重函数[17]：

式中：ωstart为初始惯性权重；ωend为终止惯性权重；t为当前迭代次数；tmax为算法总迭代次数；k为控制因子（一般取0.6）。一般情况下取ωstart为0.9，ωend为0.4。整个搜索过程是一个循环迭代过程，终止条件设为最大循环代数[18]。

由式（5）～（9）可见，粒子群优化（PSO）具有参数少的优点，粒子群算法只有c1、c2、ω等一些参数，使得操作简单，进而上手容易，易于实现优化的目的。最终达到函数优化的目的，而改进后的粒子群算法可使得式（4）中的f在短时间内取得全局最优解，即f的极小值。粒子群算法因为效率高、具备寻优原理简单、可调整参数少、并行搜索和全局收敛等诸多优点，已被应用到许多领域。

2.3 干扰源定位整体算法流程

（1）在使用粒子群算法前，先设置列车8种速度下所测点的个数。

（2） 初始化粒子群，随机生成一组粒子的位置和速度，初始化个体最优值（pb）和全局最优值（gb）。

（3） 计算每个粒子的目标函数值，作为粒子的适应度值。

（4） 将每个粒子的适应度值与其个体最优值（pb）进行比较，比较方法使用上述模拟退火法中Metropolis准则，如果当前粒子适应度值更好，则将其作为新的pb。

（5） 将更新粒子的pb与种群当前最优值（gb）进行比较，比较方法使用上述模拟退火法中Metropolis准则。如果优于当前gb值，则将其值作为当前组新的gb。

（6） 根据式（5）和式（6）更新粒子的速度和位置。

（7） 判断是否满足终止条件。如果满足，则停止算法并输出gb；如果不满足，请返回步骤3。

（8） 最后输出迭代次数与适应度的关系图以及利用粒子群算法得到的干扰源位置坐标和与实际干扰源位置的误差。

图2所示为PSO算法的流程图。

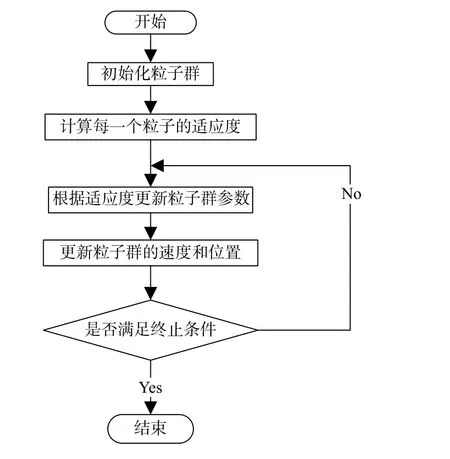
图2 PSO算法流程图Fig. 2 PSO algorithm flow chart

3 场景仿真

在实验环境下，列车在1条200 m长的直线线路上匀速行驶，根据设置好的8种速度进行仿真实验，假设干扰源位置（X0，Y0），通过式（3）并加入一些随机噪声的方法可得到各点的Si。利用MATLAB软件进行干扰源定位的仿真。已知RSSI公式中的A=-21.074 2。以下是场景仿真的优化流程：

（1） 初始化线路参数和列车运行参数；设置粒子群算法参数，设置群体个数N=80，群体维数D=2，最大迭代次数=100，惯性权重ω=0.8；设置实际干扰源位置为（103，15）。

（2） 设置2、4、5、8、10、20、25、40 m/s共8种速度，按照0.1 s采样周期计算位置(xi,yi)处的Si，加入随机噪声作为定位算法的仿真数据。

（3） 分别采用基本的粒子群优化算法和改进后的粒子群算法，根据仿真数据进行干扰源定位搜索，其全局最优解即为求得的干扰源定位。

（4） 图3是8种不同速度下，使用基本粒子群算法的迭代次数与适应度的关系图。

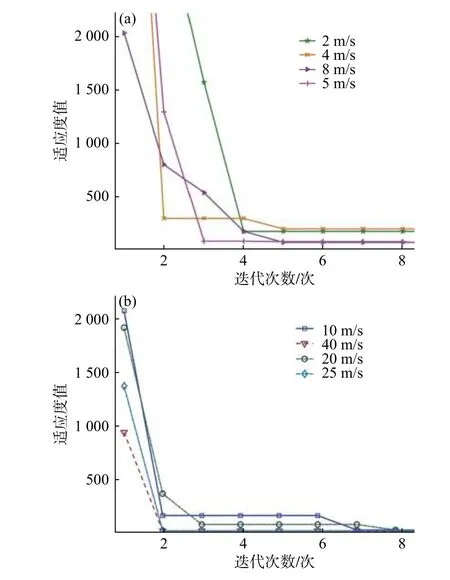
图3 使用基本粒子群算法的迭代次数与适应度的关系Fig. 3 The relationship between the number of iterations and fitness using the basic particle swarm algorithm

（5） 将不同列车运行速度下的定位结果进行比较，各取50组数据并求平均值，得到仿真结果如表1所示。

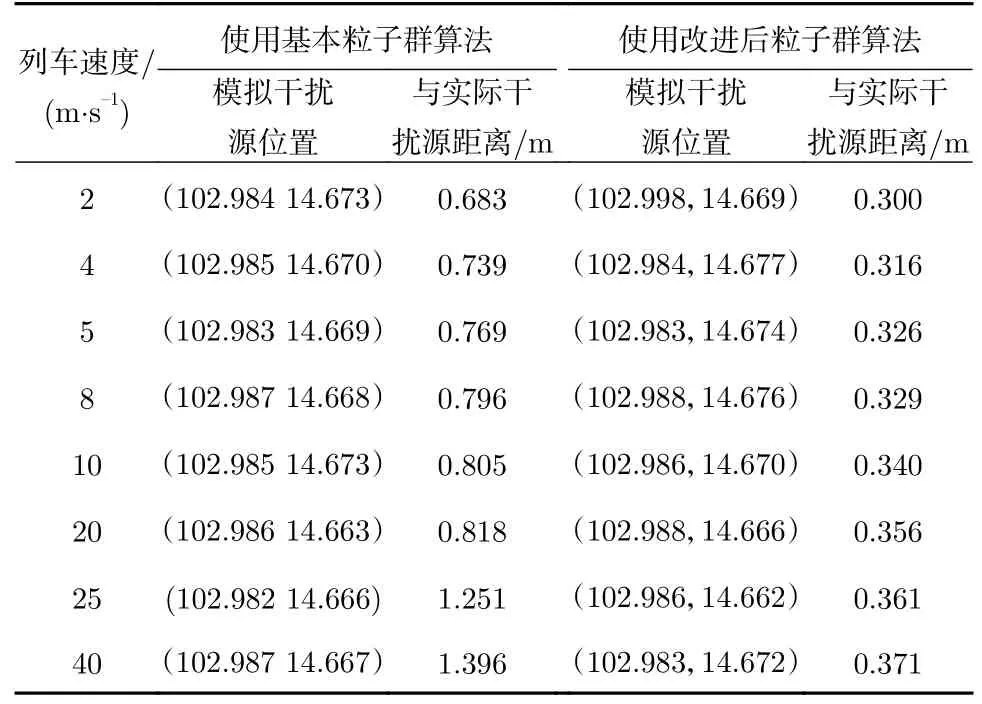
表1 仿真干扰源位置表Tab. 1 Simulated interference source location table

（6） 图4是列车在速度为4 m/s的情况下，使用不同粒子群算法的迭代次数与适应度的关系图。

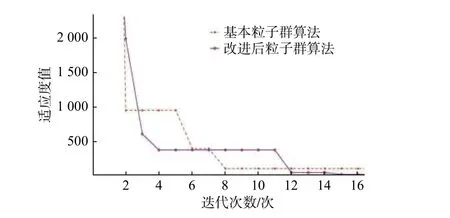
图4 速度为4 m/s 的情况下，使用不同粒子群算法的迭代次数与适应度的关系图Fig. 4 At a speed of 4 m/s , the relationship between the number of iterations and fitness of different particle swarm algorithms

如图3所示，当速度越小时，迭代次数为0时，粒子的适应度越大，换句话，粒子群迭代次数也会更小；由图3可知，在相同迭代2次后，列车速度越小，适应度函数的值下降的幅度越大；同样，列车速度越大，适应度值变成0所需要的迭代次数越多。

由表1不同速度下得到的模拟干扰源位置可见，当列车速度越快，得到的模拟干扰源位置与真实干扰源位置相差越大；由表1可知，使用基本粒子群算法和使用改进后粒子群算法得到的结果有较大的差异，使用改进后的粒子群算法，使得模拟干扰源的位置更靠近真实干扰位置，与实际干扰源距离更近。

从有关文献中可知，基本的PSO算法在搜索的初期收敛速度很快。从图4的对比可知，改进后的算法初期收敛速度较基本算法慢，且最后收敛的适应度值更小。

综上所述，实验结果与模拟列车运行的速度有关，由此可知，列车速度越低，收到的RSSI信息越有效，定位精度也越高；改进后的粒子群算法优于基本粒子群算法，在一定程度上，可使粒子避免进入局部最优，最终得到较好的结果。

4 结语

利用MATLAB仿真工具模拟了列车运行的实际场景，通过信号强度RSSI的数据进行对干扰源的测距，再利用改进后的粒子群算法不停迭代找出最优解，即模拟干扰源位置，使得模拟干扰源不断逼近真实干扰源，最终得到最优解。实验结果表明干扰源定位的精度与模拟列车运行的速度有关，通过分析得出列车速度越低，收到的RSSI信息越有效，定位精度也越高的结论。将基本粒子群算法和使用改进后粒子群算法的结果进行对比，发现改进后的粒子群算法对干扰源的定位效果更好，更适用于本实验。对于轨道交通干扰源识别与定位的研究，仅仅从信号强度角度出发来确定干扰源位置，研究方法有一定的局限性。未来，对于地铁内无线干扰源的定位研究，可以通过建立丰富的环境指纹库来开展研究，同时针对不同的列车运行速度采用不同的采样率，在定位方法上再辅以无线电传播时间差等多种技术手段，以增强精准度。