基于MDLatLRR和KPCA的光场图像全聚焦融合

黄泽丰，杨莘，邓慧萍，李青松

（武汉科技大学 信息科学与工程学院， 武汉 430081）

0 引言

传统相机在拍照时会丢失光线分布的信息，而光场相机可以同时捕获光线的角度和空间信息，能在不减少光圈的情况下扩展相机的景深，从而缩短曝光时间并降低图像噪声［1］。光场相机可以在一次拍摄中直接捕获光线场，但会牺牲成像的空间分辨率和角度分辨率，因此所成像的空间分辨率低于原生图像传感器生成的图像［2］。为了弥补上述缺点，对光场进行重聚焦从而有效提升光场图像的空间分辨率。光场数字重聚焦通过将光线从主透镜平面重新投影到新的平面上来生成重聚焦图像，经过重聚焦后的图像其聚焦区域的清晰度得到提高。多聚焦图像融合通过从同一场景多幅部分聚焦的图像中创建一个全局聚焦的图像来扩展光学透镜视场深度［3］。光场图像全聚焦融合通过结合多聚焦图像融合与光场数字重聚焦，从而获得全局聚焦的光场图像。传统的多聚焦图像融合算法主要分为空间域和变换域两类。空间域方法基于像素强度来处理并融合图像；变换域方法通过某种变换将源图像分解成不同的子带图像，然后用不同的融合规则对各子带进行融合。此外，随着神经网络技术的发展，基于深度学习的图像融合方法也开始崭露头角。

近两年，基于光场数字重聚焦的全聚焦图像融合方法逐渐流行。武迎春等［4］使用边缘增强型引导滤波对经三尺度分解后的重聚焦图像进行优化并生成全聚焦图像，该方法能补偿因光场标定误差而丢失的边缘信息并提高了全聚焦图像的清晰度。谢颖贤等［5］使用离散小波变换对重聚图像进行分解，随后对各分量采用不同融合规则来生成全聚焦图像，该方法避免了因融合产生的块效应并优化了图像的视觉效果。苏博妮［6］将重聚焦图像按亮度和色度通道分别进行处理来生成全聚焦图像，该方法能有效提高光场全聚焦图像的空间分辨率。使用光场数字重聚焦生成的重聚焦图像不受由相机调焦引起的成像范围及成像角度的限制，为全聚焦图像的生成提供了便利。

本文提出了一种基于多尺度潜在低秩分解（Multi-level image Decomposition base on Latent Low-Rank Representation， MDLatLRR）的光场全聚焦融合算法。算法将多尺度潜在低秩分解引入光场全聚焦图像融合，经分解得到的基础层保留了图像的结构信息，显著层保留了图像的边缘信息和纹理细节。对各层的特征提取算法进行改进，基础层用局部双区域窗代替八邻域窗，使计算得到的图像锐度能更加精确；显著层使用基于引导滤波的多尺度视觉显著性提取算法，增强了视觉显著性提取能力。引入核主成分分析（Kernal Principal Component Analysis， KPCA）对各层特征系数进行融合，生成由基础层图像锐度和显著层视觉显著性共同决定的聚焦决策图。

1 光场图像数字重聚焦

与传统图像不同，光场图像通常使用四维双平面参数化模型L(u，v，s，t)来进行表示，其中，L表示光线的强度；(u，v)为主透镜平面，用于控制角度分辨率；(s，t)为传感器平面，用于控制空间分辨率。通过对双平面参数进行积分，可获得聚焦平面的积分图像，表示为

通过对光场重新投影，使光线由传感器平面投影到重聚焦平面上，然后对其进行积分便可得到重聚焦图像，即

式中，ω代表聚焦系数。通过调节聚焦系数，能将光场聚焦在不同平面上。光场重聚焦参数化模型如图1所示。

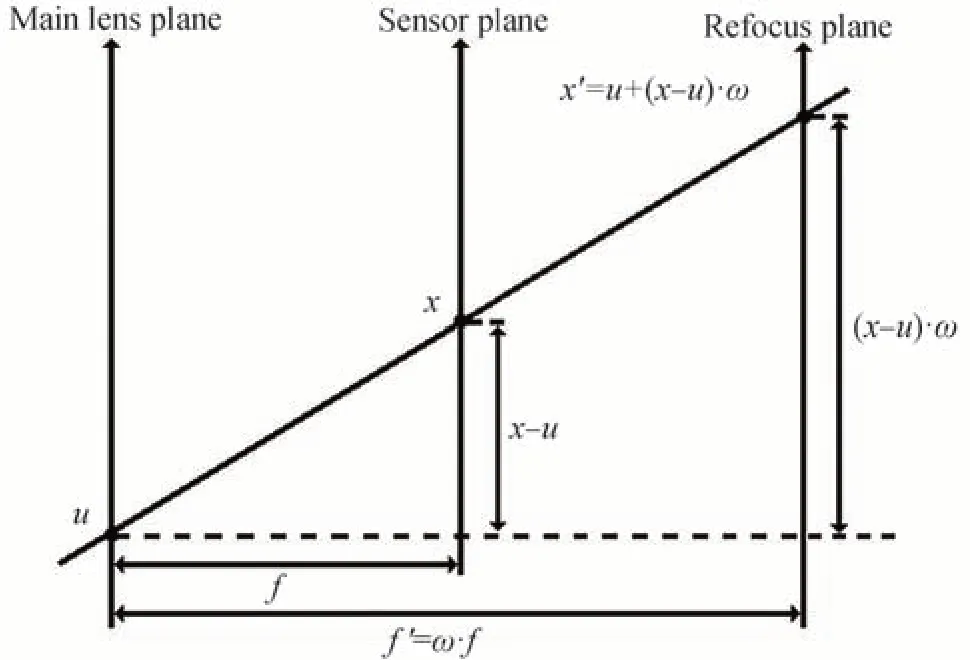
图1 光场图像数字重聚焦参数化模型Fig.1 Digital refocusing parameterization model of light field image

2 基于多尺度潜在低秩分解的光场图像全聚焦融合原理

基于多尺度潜在低秩分解和核主成分分析的光场图像全聚焦融合算法流程如图2 所示。首先通过对4D 光场图像进行光场数字重聚焦得到聚焦于不同深度的重聚焦图像。为了更为细致地提取各重聚焦图像的聚焦特征，采用多尺度潜在低秩分解将重聚焦图像分解为基础层和显著层，随后针对基础层和显著层各自的特性分别采用不同的算法进行特征提取：基础层包含重聚焦图像的结构信息，通过分析局部梯度变化情况能得到聚焦区域的大致轮廓；显著层包含重聚焦图像的纹理细节和显著目标，计算视觉显著性能反映聚焦区域的边缘信息，使得聚焦区域的判决更为准确可靠。聚焦决策图的生成由各层特征系数决定，用核主成分分析对特征系数进行降维融合，融合后的特征系数综合了基础层和显著层各自的特征。最后由融合特征系数生成聚焦决策图，引导重聚焦图像的融合并得到光场全聚焦图像。

图2 基于多尺度潜在低秩分解的光场全聚焦图像融合算法流程Fig.2 Full-focus image fusion algorithm flow of light field based on multi-scale latent low-rank decomposition

2.1 多尺度潜在低秩分解

对于一个数据矩阵，可以将其看作在完备字典下的线性组合，具体表示为

式中，X为数据矩阵，Z为系数矩阵，D为完备字典。低秩表示法在式（3）的基础上通过使用数据矩阵本身作为字典来实现数据矩阵的子空间分割。该过程可表示为

式中，||⋅ ||*代表矩阵的核范数，表示矩阵的奇异值之和。低秩表示法希望系数矩阵Z的核范数尽可能地小。当数据采样不足时，系数矩阵Z只能取单位矩阵作为唯一解从而造成低秩表示失败，这种现象被称作隐藏效应。

潜在低秩表示法在低秩表示法的基础上将解决隐藏效应转换为对凸优化问题的求解，具体可以表示为

式中，λ表示大于零的平衡系数，||⋅||*和||⋅||1分别代表核范数和L1 范数，H是显著系数的投影矩阵，E是系数噪声矩阵。一旦得到投影矩阵，就可将其用于提取图像的显著信息。

潜在低秩分解首先对投影矩阵与输入图像的乘积进行重构来得到图像的显著层，然后使用输入图像减去显著图像得到基础层。多尺度潜在低秩分解则是对基础层继续进行潜在低秩分解，从而得到更加丰富的显著信息。经过多尺度潜在低秩分解后，输入图像被分解为一个基础层和若干个显著层，基础层保留输入图像的低频信息；显著层实现对输入图像细节纹理和显著目标等高频信息的提取；随着迭代次数的增加，显著层对输入图像的特征提取能力得到增强，对细节纹理以及显著目标的提取更为精确。

本文算法使用三尺度潜在低秩分解对各重聚焦图像进行分解：首先对输入图像进行潜在低秩分解得到初始基础层和显著层一层，随后将初始基础层作为输入图像再次进行潜在低秩分解，如此往复直至分解至第三层，最后将第三次分解得到的基础层作为三尺度潜在低秩分解的基础层，分解结果如图3 所示。其中，基础层包含源图像的主要结构，如图3（b）所示；显著层随着分解尺度的迭代显著细节逐渐得到突出，如图3（c）～（e）所示。

图3 三尺度潜在低秩分解结果Fig.3 Results of three-scale latent low-rank decomposition

2.2 基础层特征系数矩阵求解

基础层保留了重聚焦图像中的结构信息以及因分解产生的伪影。在重聚焦图像中，聚焦区域像素灰度值的变化通常大于散焦区域像素灰度值的变化，而梯度反映了灰度值的变化程度。此外，像素与其相邻像素之间的梯度差代表了图像的锐度，计算图像的锐度可以扩大一个像素与其相邻像素之间的差异，将有益于聚焦和散焦区域的判定。文献［7］提出了一种基于八邻域图像梯度差值的聚焦点检测算法，该算法中单像素点图像锐度值S(i，j)计算公式为

式中，G(i，j)表示位于坐标(i，j)处像素的梯度值。该方法通过计算源图像在梯度域中每个像素与其八邻域像素的梯度差值的平方和从而得到源图像的锐度。该方法具有速度快且高效的优点，但是在计算局部图像锐度时因易受水平和垂直方向的能量抵消而导致抗噪性能下降。

在式（6）基础上对原有方法加以改进，将基于像素点的八邻域拓展到以像素点为中心向外辐射的5×5局部窗，并根据与中心的距离将窗内像素点划分为内、外两个区域Ω1和Ω2，如图4（b）所示。对内部区域Ω1使用梯度差平方和来扩大目标像素与其四邻域像素之间的差异；对外部区域Ω2使用受L2 范数约束的梯度差来统计周边区域对目标像素的影响。改进后的算法对噪声具有更高的鲁棒性并能保留更为丰富的梯度信息。局部锐度值Slocal的具体定义为

图4 局部梯度差值加权法Fig.4 Local step difference weighting method

式中，SΩp(i，j)代表位于坐标(i，j)处的像素值在区域Ωp中(p∈{1，2})的锐度值；|Ω1|和|Ω2|作为权重系数分别取4 和20，代表对应区域包含的像素数目；||⋅||2表示L2 范数。

基于本文方法和文献［7］方法的图像锐度提取结果分别如图4（c）和（d）所示。通过对比两算法生成的锐度矩阵可知：基于局部窗的图像锐度算法具有更强的鲁棒性，生成的图像锐度矩阵受散焦区域噪声的影响更小，且能更精确地反映聚焦区域边界的梯度变化情况。

2.3 显著层特征系数矩阵求解

显著层保留了源图像中的细节信息和显著特征。显著特征在重聚焦图像中表现为对聚焦区域的突出，而细节信息的保留很大程度上决定了全聚焦图像质量。通过对重聚焦图像的显著层进行视觉显著性检测可以得到较为准确的聚焦区域。MA J 等［8］提出了一种简单有效的图像视觉显著性计算方法，该算法通过衡量每个像素与图像中其他所有像素的对比度来表示该像素的显著性。对于灰度级p，图像中对应像素的显著性R(p)可以表示为

式中，η(p)代表图像中灰度值p对应的像素数目，τ为灰度值，P为灰度级数。该方法虽然可以快速计算出图像的视觉显著性，但所获结果易受源图像影响进而在聚焦区域之外产生较大权值，如图5（b）中间位置处的盆景轮廓和位于右下方的果盘虚影。

图5 多尺度迭代显著性检测算法Fig.5 Multi-scale iterative significance detection algorithm

针对此问题提出了一种新的多尺度图像显著性提取方法，具体步骤包括：1）将直接对源图像进行显著性矩阵计算改变为在梯度域进行；2）通过引导滤波对显著性矩阵进行优化；3）将单尺度显著性检测改进为基于引导滤波的多尺度迭代显著性检测。

首先，计算源图像中每个像素的梯度值，计算公式为

用Sobel 算子来计算图像梯度，∇x f与∇y f分别表示源图像在水平和竖直方向上的梯度值。

其次，计算源图像在梯度域中的显著性矩阵，公式为

式中，Gkn表示第n张重聚焦图中第k层显著层的梯度图像，N为重聚焦图像总数；R(⋅)表示图像显著性矩阵；Vkn，1代表源图像在单尺度下的梯度域显著性矩阵。所获结果与原方法相比，位于聚焦区域之外的误判区域权值得到抑制，如图5（c）所示。

最后，将对应显著层源图像作为引导图像对单尺度梯度域显著性矩阵进行引导，随后重复该过程并使之与前次结果进行叠加，具体过程为

式中，Fguidedfilter(⋅)表示引导滤波函数，fkn表示第n张重聚焦图中第k层显著层源图像，s表示当前尺度系数，M为总迭代次数，ε为引导滤波正则化系数，本文设为0.001。在不同尺度下使用显著层源图像作为引导图像对显著性矩阵进行引导滤波，可以使显著性矩阵保留引导图像的结构且不丢失边缘信息。在不同迭代次数下生成的显著性矩阵结果如图5（d）～（h）所示。从图中可以看出，随着迭代次数的增加，聚焦区域的突出程度也越来越高，当迭代次数达到4 次时，对聚焦区域的提取已相当精准，之后的迭代对于显著性提取影响甚微。

为了进一步对比不同尺度下显著层的特征提取能力，选用方差、信息熵和均方根误差等指标对1 至6 次迭代下梯度域显著性提取结果进行对比，其中：方差和信息熵分别描述显著性矩阵的细节保留以及显著信息提取的能力，方差越高反映了保留的细节和纹理越丰富，信息熵越高则反映显著性矩阵对输入图像的显著信息提取能力更强；此外，通过计算显著性矩阵和输入图像梯度图之间的均方根误差，能反映不同迭代次数下的显著目标提取准确度，越小的均方根误差表示检测效果越精确。为统筹考虑各项指标，对各结果经过归一化后的三个指标进行叠加得到综合评定分数，定义为

式中，Vs，s∈{1，...，6}表示在1 至6 次迭代次数下生成的显著性矩阵；Qvariance、Qentropy和Qrmse分别计算显著性矩阵的方差、信息熵以及与梯度图像G的均方根误差，并在计算完后对结果进行归一化。图6 反映了不同迭代次数下各显著性矩阵的得分情况，可以看出随着迭代次数增加，显著性矩阵的性能得到提升，并在第三次达到拐点随后增长缓慢。为了减少计算量并降低时间成本，将迭代次数选定为4 次。

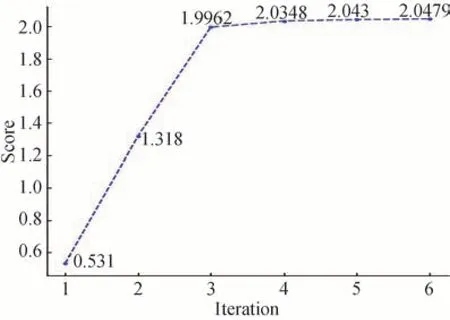
图6 不同迭代次数下显著性矩阵得分情况Fig.6 Score of salient matrix under different iterations

2.4 基于核主成分分析的聚焦决策图生成及融合

核主成分分析［9］是主成分分析的一种非线性推广，将输入数据映射到高维特征空间中，然后对主成分进行分析。该方法可将高维数据降至低维并保留主要成分以及提取特征信息，且其效果优于同类其他方法［10］。在本文中，光场重聚焦图像经三尺度潜在低秩分解得到了一个基础层和三个显著层，算法框架如图7所示。聚焦决策图生成详细步骤为：

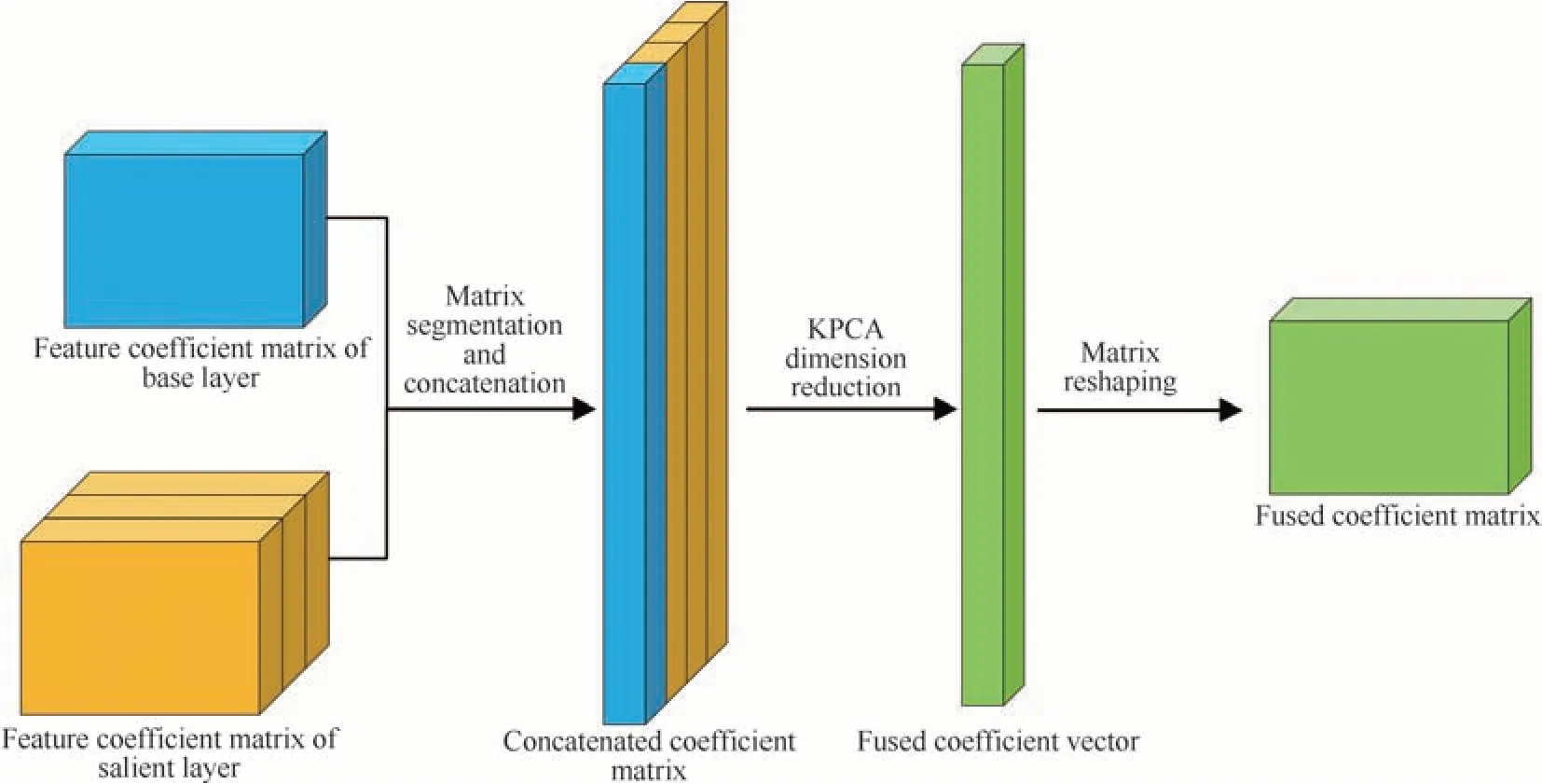
图7 基于核主成分分析的特征系数矩阵融合算法框架Fig.7 Framework of eigencoefficient matrix fusion algorithm based on kernel principal component analysis

1）为提高算法运行效率，对基础层和显著层的特征系数矩阵进行分割，将特征系数矩阵分解为M2个子矩阵，该过程可表示为

式中，fnij表示子矩阵，i和j为子矩阵在原矩阵中的对应位置。子矩阵的尺寸会影响降维的时间成本和降维融合效果，所用源图像大小为1 024×1 024，在实验过程中分别使用32×32、16×16 和8×8 的子矩阵，经过对比发现：32×32 子矩阵所需要的时间成本是其余尺寸的2 倍及以上；8×8 子矩阵时间成本最低，但由于尺寸过小导致最终降维融合的效果不如16×16 子矩阵。综合考虑，将子矩阵大小定为16×16，则M=分割完成后，对所有子矩阵进行向量化重组，在对其他特征系数矩阵进行同样操作后将所有向量进行组合，即

式中，vnij是对式（14）中的子矩阵fnij进行向量化后的结果；Y为4，表示特征系数向量总数。各分割特征系数向量经过组合后得到分割特征系数矩阵Fcombine，将原本三维的数据降至二维。

2）使用核主成分分析对分割特征系数矩阵进行降维处理：先用非线性映射Φ(xi)将输入的分割特征系数矩阵Fcombine中的元素xi(i=1，…，Y)映射到高维特征空间中使其线性可分，然后在这个高维空间中进行主成分分析降维。高维特征空间中的协方差矩阵定义为

由于非线性映射Φ(xi)是未知的，需要通过选取合适的核函数k，将对协方差矩阵C的操作转化为对核矩阵K特征值求解的问题。核矩阵K表现形式为

采用高斯核函数，其定义为

σ为标准差。可知，Kij=k(xi，xj)=Φ(xi)Φ(xj)。随后，求解核矩阵K的特征值λ以及经过标准化的特征向量。特征向量υ的标准化定义为

为了实现非线性映射的中心化，还需要对核矩阵K进行中心化处理。定义OY为Y×Y的全1 矩阵，则经过中心化后的核矩阵表示为

3）分割特征系数Fcombine经过降维得到了融合特征系数向量，对每个重聚焦图像的融合特征系数向量进行重塑得到对应的重塑系数矩阵Fnfused，n∈{1，…，N}，N为重聚焦图像总数。采用取最大值规则对所有融合特征矩阵中的每个像素点进行判决，得到初始决策图Iinitial中每个像素值的表示

由于初始决策图的构建可能受聚焦区域中存在的一些散焦块影响从而产生小的误判区域，所以要对初始决策图执行小结构去除来优化决策图。具体过程可以表示为

式中，Fssr(⋅)为小结构去除函数，ψ为判决阈值，当图像中存在像素数目小于ψ的区域时会被去除，ψ设置为各张重聚焦图像初始决策图中聚焦区域像素总数的5%。

得到最终决策图后，使用重聚焦图像作为引导图像来对聚焦决策图进行引导滤波从而削减模糊边界的影响，全聚焦图像Iaif可以表示为

式中，N代表光场重聚焦图像的数量，rf和εf分别为引导滤波函数尺度系数和正则化系数，I代表光场重聚焦图像；Iinitial代表最终决策图。

3 实验结果与分析

实验使用的硬件配置为：CPU：Intel Core i7-11800H；RAM：32.0 GB；GPU：GeForce RTX 3060，实验环境为Matlab R2019a。实验分为两部分：1）选用多个4D 光场子孔径图像组进行全聚焦融合实验以验证本文算法的有效性；2）与其他先进的多聚焦图像融合方法从主观和客观两方面进行比较以评估本文算法性能。

3.1 光场全聚焦融合实验

实验数据选用HCI 数据集［11］提供的4D 光场数据，每组数据均包含10 张重聚焦图像，实验所用部分数字重聚焦图像及对应聚焦决策图如图8 所示。图8 展示了从4 组光场数据集中选出的3 张光场数字重聚焦图像以及由本文方法生成的聚焦决策图。图9 展示了4 组全聚焦融合实验的总聚焦决策图以及对应的光场全聚焦图像，其中，第一、第三列为总聚焦决策图；第二、第四列为全聚焦图像。通过对比图8 和图9 可以发现，总聚焦决策图中不同颜色对应各单一聚焦决策图，此外，本文方法在处理聚焦区域模糊边界问题上用重聚焦图像作为引导图像对聚焦决策图进行引导滤波，使各聚焦决策图的衔接更为平滑，表现在总聚焦图上为不同颜色区域衔接处具有模糊效果。

图8 4 组光场重聚焦图像以及对应聚焦决策图展示Fig.8 Four groups of light field refocusing images and corresponding focusing decision map

图9 各重聚焦图像总聚焦决策图以及对应全聚焦图像展示Fig.9 The total focusing decision map of each refocusing image and the corresponding all-in-focus image are displayed

图9（a）和（b）为Herbs 图像组的总聚焦决策图和全聚焦图像，总聚焦决策图中10 个灰度级对应10 张重聚焦图像的聚焦区域，各聚焦区域囊括了Herbs 图像的所有要素：背景（墙壁）、物品（桌子上的盆景、花瓶以及果盘）、各物品间的区域（果盘、空碟和盆景三者之间的区域）以及前景（桌角和桌子外侧）。通过总聚焦决策图引导重聚焦图像进行融合便能生成全聚焦图像，观察图9（b）、（d）、（f）及（h）等全聚焦融合结果可以发现：各聚焦区域边界衔接自然、边缘信息得到良好保留，果盘中各水果轮廓以及白色立式花瓶和其左侧的植物相交处；同时，经过重聚焦后的光场图像实现了对纹理细节的增强（植物叶子、花瓶上的花纹以及背景墙上的细节），使全聚焦融合结果具有更好的视觉效果。此外，本文算法不对分解后的各层直接进行融合，而是通过生成聚焦决策图来引导重聚焦图像进行融合，所获得的全聚焦图像不会因为各层融合产生的噪声而导致图像质量下降。

3.2 多聚焦图像融合对比实验

为了进一步评估本文算法的性能，选取了6 种多聚焦图像融合算法：RW［12］、f-PCNN［13］、IFCNN［14］、MGFF［15］、MST［16］、CSR［17］来进行比较。对比实验采用LFSD［18］数据集提供的光场重聚焦图像，由于大多数方法仅针对两幅重聚焦图像的融合，所以从每组重聚焦图像中选出两张作为输入图像，共计10 组。为了保证实验结果客观公正，所选方法均使用原文提供的源代码以及最优参数。选取四大类共10 种客观评价指标［19］：1）基于人类视觉系统的指标，包括Qcv[20]、Qcb[21]、Qabf[22]，Qcv考虑局部测量来估计源图像中重要信息被融合图像的表示程度，Qcb基于人眼视觉系统模型对融合图像进行质量评价，Qabf利用人眼对比度灵敏度函数比较融合图像与源图像的视觉差异；2）基于图像梯度的指标，包括空间频率（Spatial Frequency，SF）、平均梯度（Average Gradient，AG）以及边缘强度（Edge Intensity，EI）；3）基于统计学的指标，包括方差（Variance，Var）；4）基于信息论的指标，包括信息熵（Entropy，EN）、交叉熵（Cross Entropy，CE）以及互信息量（Mutual Information，MI）。这四类指标涵盖了对人眼视觉感知、图像显著性、边缘信息量以及图像失真程度等因素的考虑，能够较为全面且客观地评价融合图像的质量。

图10 反映了实验中7 种算法在融合LoveLocks 图像组时的表现。其中，图10（a）和（b）均为重聚焦图像，（c）～（i）为所选算法各自的融合结果。为进行更细致的对比，对融合结果的细节放大处理，红框和绿框即为局部放大区域。通过对比放大区域可以发现，本文算法在对源图像的细节保留上有较为优秀的表现：右下角红框放大区域展示了各方法对锁面数字细节的保留情况，可以看出本文方法保留的数字更为清晰，每个数字都具有最好的边缘视觉效果，更符合人眼的视觉特性；右上角绿框放大区域展示了各方法对右聚焦图像与左聚焦图像模糊边界接壤处复杂纹理的融合情况，可以发现CSR 方法在该区域产生了明显的伪影，IFCNN 和MGFF 等方法的融合结果丢失了“L”型锁的表面细节，使得锁面看起来非常平滑，本文方法较f-PCNN、MST 和RW 等方法具有最高的对比度，更能凸显“L”型表面凹凸不平的细节。7 种方法在LoveLocks 图像组上的融合结果客观指标如表1 所示，其中，最优值以红色表示，次优值以蓝色表示。10 种评价指标中，除Qcv和交叉熵（CE）为越小越好外，其余均为数值越大越好。可以看出，本文方法的融合结果在10 个指标中具有3 个第一和4 个第二，在Qcv、互信息量以及交叉熵均取得了第一名，说明经本文算法生成的融合图像较好地保留了源图像的细节纹理并具有更优的视觉表现。

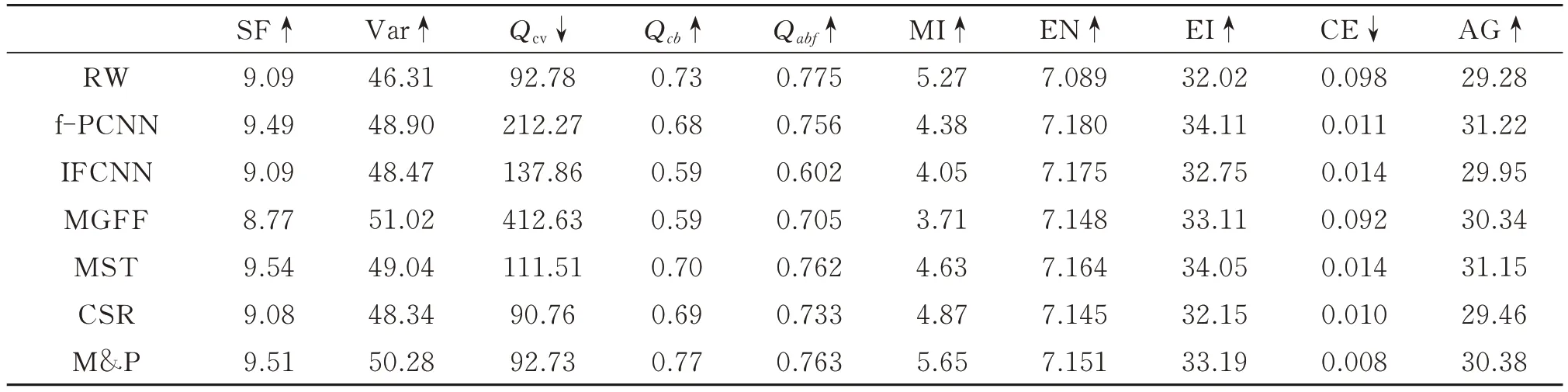
表1 LoveLocks 图像在7 种融合算法上的客观指标对比Table 1 Objective index comparison of LoveLocks image on seven fusion algorithms

图10 LoveLocks 图像融合结果对比Fig.10 LoveLocks image fusion results comparison

图11 与图10 具有相同的内容分布，反映了7 种算法在融合Edelweiss 图像组时的表现。红框放大部分反映了各方法对啤酒商标的细节保留情况，可以发现CSR、IFCNN 和RW 等方法产生了明显的伪影，MGFF方法未产生伪影但其商标清晰度有所下降，f-PCNN、MST 和本文方法在主观上均有较好表现，但从表2 中的数据可以看出本文方法具有最好的互信息量以及信息熵，说明本文方法对源图像的信息保留程度更高。绿框放大区域反映了在面对左右聚焦图像模糊边界区域时，各方法对背景（天空等均匀区域）和显著目标（教堂塔尖）的融合情况，可以看出，除RW 和本文方法外，其余5 种方法在塔尖区域均有非常明显的伪影，进一步仔细对比可以发现，经本文方法融合后的结果没有伪影，塔尖与天空融合后的视觉效果要好于RW方法。

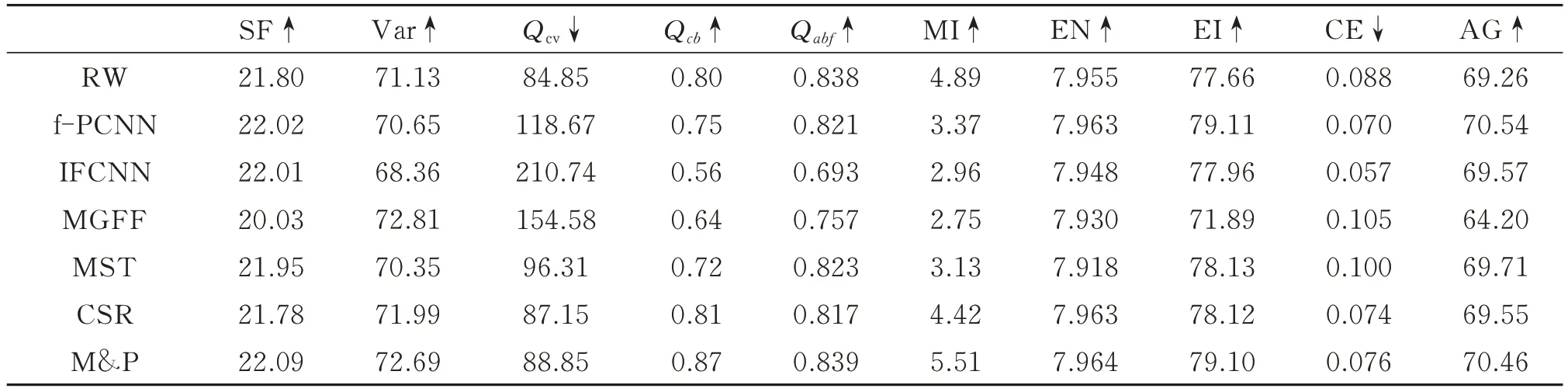
表2 Edelweiss 图像在7 种融合算法上的客观指标对比Table 2 Objective index comparison of Edelweiss images on seven fusion algorithms

图11 Edelweiss 图像融合结果对比Fig.11 Edelweiss image fusion results comparison

表2 反映了7 种方法在Edelweiss 图像组上的融合结果客观指标对比，本文方法在除Qcv和交叉熵以外的8 种指标上均取得较为优秀的表现。Qcv反映了源图像中的重要信息在融合图像中的表示程度，由表2 可知，RW 方法和CSR 方法的Edelweiss 融合结果在Qcv指标上取得了良好的成绩，但在图11 中的红框放大区域，可以看出RW 方法和CSR 方法的融合结果具有明显的伪影，推测正是因为这些伪影导致Qcv值的异常。

为了使7 种方法融合结果指标对比更为公正客观，对10 组融合结果的评价指标求平均值，如表3 所示。由表3 可知，本文算法在4 类客观指标中均有较好表现，在空间频率、Qcb、互信息量、信息熵、边缘强度和交叉熵这6 个指标中取得了最优值，其中空间频率和互信息量表现尤为突出，说明经本算法生成的全聚焦图像具有更清晰的细节和纹理且对重聚焦图像具有更强的信息保留能力。本文算法在剩下4 个指标中均为次优值，其中，MGFF 方法虽然具有最高的方差，但在3 个视觉指标中的表现较差，这可能是由于MGFF 方法所产生的融合图像会在边界处会产生伪影，从而导致其方差虚高；两个视觉指标Qcv和Qabf与最优指标非常贴近且远高于排名第三的指标。综上所述，经本文算法生成的多聚焦图像与其他6 种方法相比具有清晰度高、视觉效果优秀、图像对比度高等特点。

表4 给出了7 种方法在10 组多聚焦融合实验中所需要的平均时间成本。可以看出，MST、MGFF 以及IFCNN 三种方法均具有较低的时间成本，但在客观指标上的表现却不佳：MST 方法具有最低的时间成本，但仅取得了空间频率次优的成绩，MGFF 方法仅在方差上获得了最优值，IFCNN 方法在10 项客观指标中均表现平庸。本文方法的时间成本低于CSR 方法和f-PCNN 方法，综合看来，本文方法取得了良好的融合效果，但是由于引入核主成分分析对各层特征系数进行融合从而导致了时间成本较高。

表4 7 种融合算法的平均时间成本Table 4 Average time cost of seven fusion algorithms

4 结论

本文提出了一种基于多尺度潜在低秩分解的光场全聚焦图像融合方法。通过对4D 光场图像进行数字重聚焦，将焦点聚集到图像中的各个目标上从而得到重聚焦图像，然后将重聚焦图像作为输入图像来实行全聚焦融合。本文引入多尺度潜在低秩分解对重聚焦图像进行分解，使用局部双区域梯度差值加权平均算法和可迭代引导滤波视觉显著性提取算法来计算各层特征信息，最后使用基于核主成分分析的特征系数融合算法生成聚焦决策图并引导全聚焦图像的生成。实验结果表明，经本文方法生成的光场全聚焦图像具有良好的视觉效果以及更高的空间分辨率；与近年提出的基于传统或深度学习的多聚焦图像融合算法相比，本文算法在所选4 类客观评价指标中均有良好表现，验证了其有效性。实验过程中选用灰度图像作为输入图像，目的是为了减少计算量和时间成本，本文算法也同样适用于彩色光场图像的全聚焦融合。此外，该算法也存在不足之处，在各重聚焦图像聚焦边界区域的处理上，仅采用引导滤波对其进行平滑融合，并未做出进一步的优化，今后将对模糊边界区域的融合规则进行研究，使生成的全聚焦图像具有更好的视觉表现。