基于稀疏先验的合成孔径光学系统的图像复原方法

钟烁，范斌，刘盾，苏海冰，张豪，杨虎，NIKONOROV Artem

（1 中国科学院光电技术研究所 薄膜相机总体室， 成都 610209）

（2 中国科学院大学， 北京 100049）

（3 萨马拉国立研究大学，俄罗斯 萨马拉 443086）

0 引言

随着世界各国科技的不断进步，高分辨率光学成像技术不论是在资源探测还是在对地观测等领域都得到了越来越广泛的应用［1］。在光学系统中，如果只考虑光瞳产生的衍射限制，固定入射波长，则分辨率大小与孔径大小成正比。但是由于孔径大小受到光学元件的材料、加工以及载荷重量等诸多因素的影响，无法一味的增大单个孔径大小来提升成像分辨率。合成孔径技术使用多个子孔径在空间中按照一定的排列方式来获得与单一大孔径等效的分辨率，是一种成本更低、易于实现的方式［2-3］。

合成孔径技术随之带来的问题是成像的降质模糊，原因主要有以下两个方面：（1）子孔径拼接带来通光面积的减少，引起系统的点扩散函数（Point Spread Function， PSF）发生变化，进而导致光学传递函数在中低频部分的衰减［4］；（2）合成孔径系统在光路搭建和仪器组装过程中造成了共相误差，共相误差使各个子孔径的光束不再具有相同的相位，经过每个子孔径的光束在到达像面后无法形成干涉，从而导致最终成像图像的模糊，严重时甚至无法成像［5］。以上共同导致合成孔径系统成像的质量退化，对于一些较大的误差可以通过改进或者调试光学系统解决，而不可避免的误差只能通过图像的角度进行复原。

FIETE R D 等最早展开对合成孔径系统成像质量的研究，分析了不同因素对图像质量的影响，总结出合成孔径系统的填充因子大小与最终成像图像的信噪比成正比［6］。随后FIENUP J R 根据FIETE R D 得出的信噪比理论，利用维纳滤波算法对合成孔径图像进行复原［6］。之后维纳滤波成为国内外进行合成孔径图像复原的主流方法，研究也主要围绕在其的改进上［7］。维纳滤波算法基于最小二乘原理，将数字图像看做二维平稳的连续信号，中心思想是使复原图像与退化前图像的均方误差最小、相似度最高［8］。虽然在已知光学系统的PSF 和噪声功率谱的情况下，维纳滤波的复原效果好，但是当无法对噪声功率谱有较好的估计时，复原效果较差，同时无法解决共相误差，复原的图像会产生振铃现象。2014年，WEI Xiaofeng 等提出结合视觉感知对图像进行分区，再使用双边滤波消除维纳滤波算法产生的振铃现象。该方法能够有效的抑制振铃现象，但是对图像的分区要求较为严苛，且仍然没有解决噪声问题［9］。2021年，TANG Ju 等首次提出训练卷积神经网络的方式对合成孔径系统图像进行复原，结果表明该方法在多场景下具有较好的复原结果［10-11］，但存在的问题是前期训练模型的过程需要大量的图像数据，复原效果也依赖于数据集，难以用在不同的应用需求中。

综上所述，目前针对合成孔径系统的图像复原方法需要较强的先验参数或是缺乏针对性，无法得到广泛的应用。而在整个图像复原领域，使用统计下的固有先验方法已经得到了广泛的应用，具有代表性的是暗通道先验理论。暗通道先验理论由HE K M 等在2011年首次提出［12］，发现对于自然清晰的图像，其暗通道值大多趋于零值，而有雾或模糊的图像其像素点暗通道值大多变为非零值。该理论简单且在多种场景得到应用［13-14］。因此本文提出一种加入暗通道的稀疏先验方法，用来还原合成孔径系统的图像。本文首先分析合成孔径系统的图像退化过程，结合图像的视觉感知，在统计和数学的角度验证暗通道先验理论对合成孔径系统进行图像复原的可行性，以此建立图像复原模型，针对L0范数最小化问题，提出使用半二次分裂法迭代求解，最终恢复清晰的图像。

1 合成孔径系统图像退化模型

合成孔径光学系统由多个子孔径在像面按一定方式排列，满足相位同步条件下在焦平面实现干涉成像，通常工作在可见光，采用线性系统理论，可以建立简单的成像过程模型

式中，*表示卷积的过程；I(x，y)和G(x，y)分别表示原始图像和退化图像；n(x，y)为成像过程中产生的噪声；h(x，y)表示光学系统的PSF，计算方式如下［15］为

式中，(x，y)为像平面坐标，λ为中心波长，f为焦距，am与bm分别为坐标轴上子孔径圆心的位置；PSFsub为系统各个子孔径的点扩散函数，表示为

式中，J1为一阶Bessel 函数；D为光瞳的直径；

合成孔径系统由于孔径拼接从而导致通光面积的减少，可以通过计算子孔径总面积与外接圆面积之比（填充因子）来表示阵列的稀疏程度［16］。以八孔径环形阵列结构为例（如图1（a）所示），与单一大孔径阵列结构对比可以发现：合成孔径系统的PSF 发生明显的弥散（如图1（b）所示），调制传递函数（Modulation Transfer Function， MTF）的主峰被压缩，周围出现多个次峰（如图1（c）（d）所示），在频谱响应能力上，合成孔径系统在中低频处响应迅速下降，尽管随着填充因子的增加，下降有所缓解，但仍然远达不到单一大孔径的水平（如图1（e）所示）。

上述现象可以归结为合成孔径系统自身阵列结构特性导致的成像退化，除此之外还需要考虑共相误差对成像的影响。共相误差主要包括活塞误差与倾斜误差，在合成孔径系统拼接过程中，共相误差需要控制在系统可以容许的范围内，此时合成干涉阵列才能近似实现共相位光束合成［17］。由于活塞误差会对图像产生更加严重的振铃现象，影响成像的质量，因此本文主要考虑活塞误差。活塞误差指不同孔径之间不在一个水平面，导致光路的光程出现偏差，此时点扩散函数可以重新表示为［18］

式中，Δφn表示第n个子孔径的活塞误差，通常取波长的倍数。

2 图像复原方法

合成孔径系统成像的退化受到诸多因素的影响，采用类似维纳滤波的方法时，需要对光学系统成像的干扰信息进行分析，包括阵列结构、共相误差、大气湍流等，获得准确的退化函数，即PSF，同时还需明确噪声功率谱比值，否则无法得到较好的复原效果。而在实际应用场景中，从图像的角度进行的成像复原希望能够采用更加明确的先验并且取得良好的泛化能力。本文提出一种基于稀疏先验的复原方法，方法引入暗通道先验，以L0范数的形式进行约束。流程如图2 所示，步骤如下：

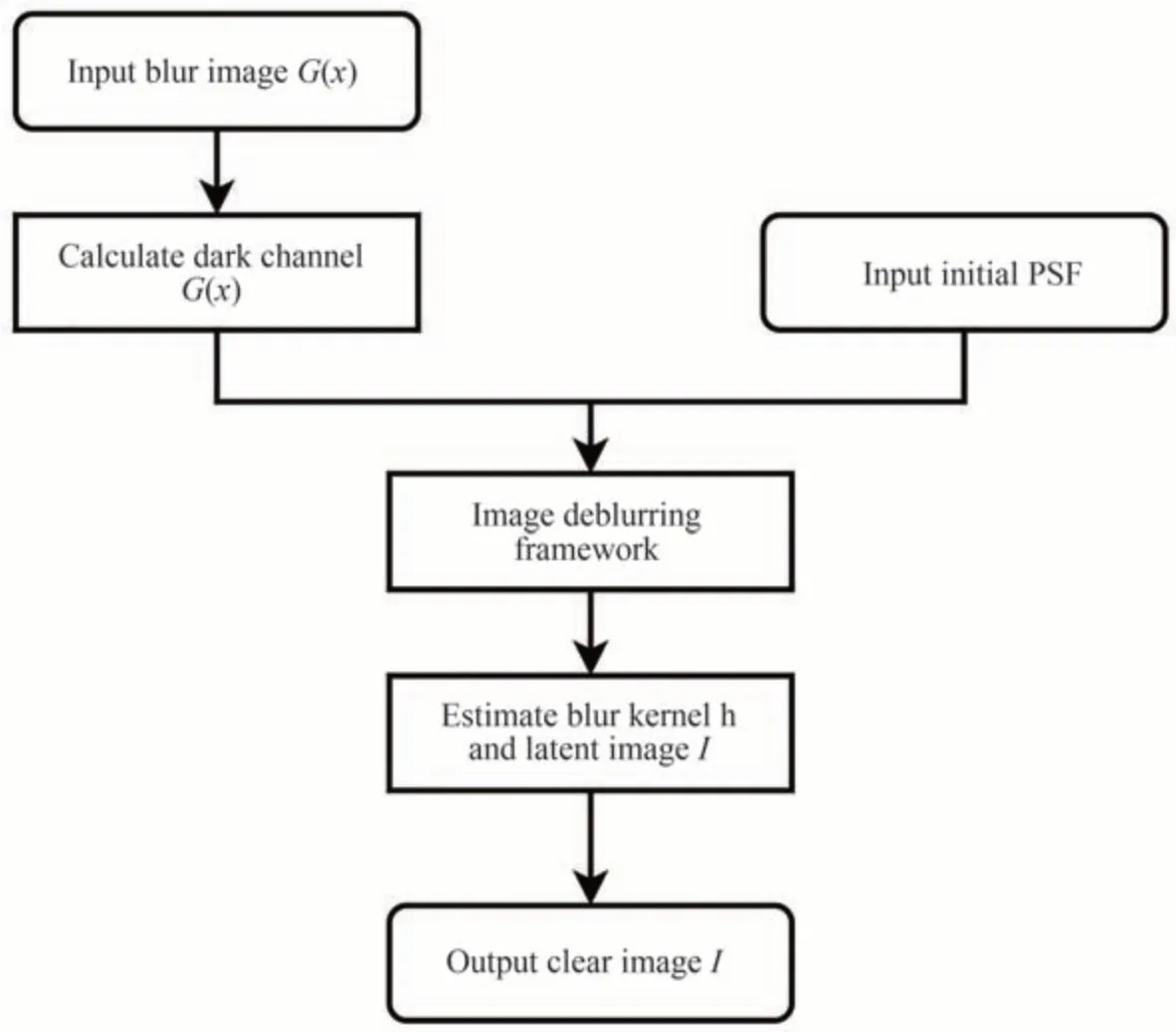
图2 图像复原方法流程Fig.2 Flow chart of image restoration method

1）计算光学系统固定阵列结构下的系统PSF。

2）设计图像去模糊的优化框架，PSF 作为初始模糊核。

3）将合成孔径系统图像的暗通道和梯度以L0范数的形式作为正则化项加入到框架中。

4）采用半二次分裂法求解目标函数。

5）输出最终的清晰图像。

2.1 暗通道先验理论

对于任意图像I，暗通道的定义为

式中，x和y分别表示图像像素点的位置；P(x)是以x为中心的邻域；c为集合{r，g，b}的颜色通道（若为灰度图，则只需进行前一项操作）。暗通道用于描述图像每个像素点位置邻域中的最小值，HE K M 等观察到，对于自然（清晰）的图像，图像暗通道值大多数为趋近于零的小值，而模糊后的图像大多数变为非极小值。

图3 原始图像与退化图像的暗通道对比Fig.3 Dark channel comparison between original image and degraded image

图4 原始图像与模糊图像的暗通道值统计图Fig.4 Dark channel statistics of clear and blurred images

此外，从数学的角度，根据式（1），在不考虑噪声的影响时，卷积的过程可以表示为

式中，Ωk表示模糊核的域；p表示模糊核的大小；易知h(z)≥0 且∑z∈Ωkh(z)=1。此时可以假设在卷积的过程中，任意邻域内的像素值的加权和不小于邻域中的最小像素值，即整个卷积的过程增加了暗通道的值，有以下命题

证明过程为

式中，Nx表示以像素点x为中心，与模糊核一样大的邻域。

若分别用D(G)和D(I)表示退化图像和原始图像的暗通道值，则有D(G)(x)≥D(I)(x)。因此本文方法引入暗通道作为稀疏先验项，用于合成孔径系统图像的复原。

2.2 模型

将图像的梯度和暗通道以L0范数的形式表示其矩阵的稀疏程度，设计如下的图像去模糊框架

论舞蹈作品表演者的作者地位 .............................杨华权 03.37

式中，第一项为保真项，用来约束估计的清晰图像和模糊核卷积后的值与模糊图像损失最小；第二项用来正则化模糊核的解，此项采用可通过快速傅里叶变换求解的L2范数；第三项用来剔除较小的梯度，而保留梯度较大的图像细节；第四项为暗通道约束项，使得估计的清晰图像暗通道稀疏程度尽可能的高。α、β和λ为权重参数。

为了求解式（9），在计算迭代过程的清晰图像I和模糊核h时，对其中一个进行替代性估计，此时便将原来的优化问题变成了两个子问题。其中估计清晰图像I的方式

估计模糊核h的方式

对于式（10），直接求解L0范数和非线性问题D(∙)较为困难，需要采用半二次分裂交替最小化算法［19-20］，首先分别引入与暗通道和梯度关联的辅助变量p和g=(gh，gv)，gh和gv分别为图像水平和垂直方向的梯度。则原公式改写为

式中，μ和ω为正惩罚参数。固定其它参数再交替最小化求解I、p和g。首先求解I，目标函数表示为

由于运算D(∙)是一个非线性的过程，因此需要用一个等价的线性运算来代替它。引入映射矩阵M，将图像I的像素映射到其暗通道，如图5 所示为映射过程，图片左侧的彩色方框表示其是所在的邻域内的最小值，数学定义为

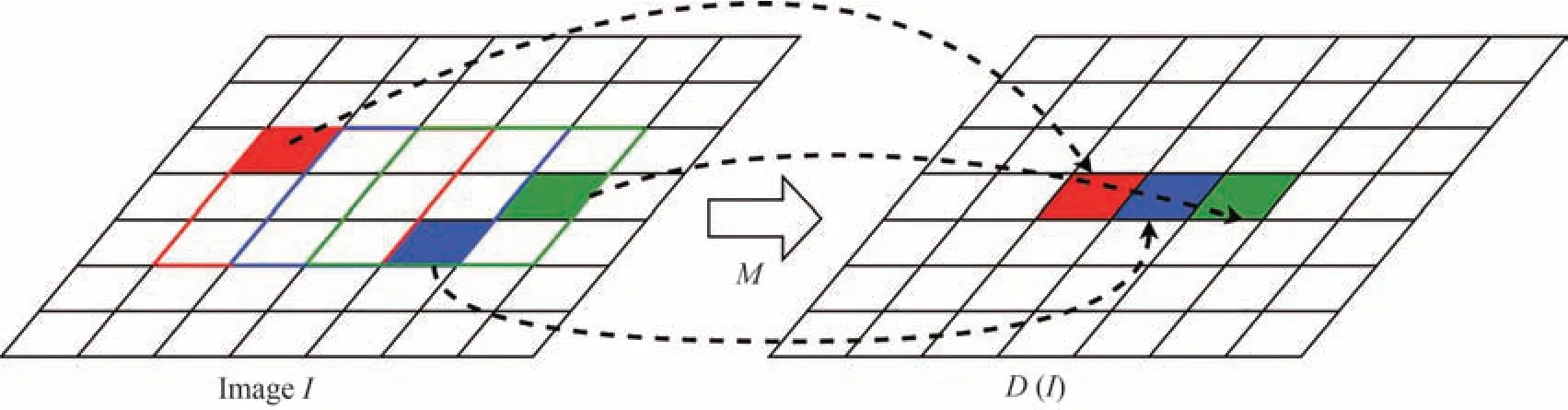
图5 暗通道矩阵映射Fig.5 Dark channel matrix mapping

得到映射矩阵M后，此时有MI=D(I)，则式（13）目标函数可以重新表示为

此时即可通过快速傅立叶变换求解I

得到I后，求解辅助变量p、g的子问题就不再涉及非线性函数运算，因此可直接表示为

式（17）、（18）均为求解像素最小化问题，以式（18）求解p为例，通过式（19）求解

最后，对式（11）使用快速傅立叶变换求解并更新模糊核h

在计算得到h后，首先将h中所有存在的负值设置为0，再进行归一化处理，此时h满足了模糊核的定义。算法1 显示了整个迭代的过程。

Algorithm 1 Deblurring Algorithm Input： Blurred image G，Initialize h with PSF for i=1： iteration do I=G， ω=2λ repeat solve for p using Eq.（18）μ=2 β repeat solve for g using Eq.（17）solve for latent image I using Eq.（15）μ=2 μ until μ>μmax ω=2ω until ω>ωmax solve for blur kernel h using Eq.（11）β=0.9 β，λ=0.9 λ end for Output： blur kernel h， result image I

3 实验与分析

本文设计了一种针对合成孔径成像系统的图像去模糊算法，方法加入暗通道作为固有的先验进行约束，根据合成孔径系统阵列结构计算的PSF 作为初始模糊核，经过迭代估计最终的复原图像。通过足够的测试，综合考虑复原质量和时间，本文方法实验时正则化项的参数分别设置为：α=2，β=λ=0.004，如无说明则迭代次数设置为5 次。为了验证算法的有效性，首先进行仿真实验，分别验证多组不同活塞误差和多场景下算法的复原能力，最后再对实验室获取的图像进行直接复原。

3.1 仿真结果与分析

首先根据2.1 节的阵列结构参数，以图1（a）中1 号孔径作为参考孔径，对其它孔径随机加入区间为0～0.3λ大小的活塞误差，共设置5 组参数（如表1 所示），然后对遥感图像进行仿真退化，如图6（a）和（b）所示，分别为原始图像和退化后图像。以式（2）计算得到阵列结构下的PSF 作为模糊核，分别进行维纳滤波（Wiener Filter， WF）方法、Richardson-Lucy（RL）方法，以及本文方法在迭代次数为1、3、5 和8 的图像复原实验。以第一组实验参数的复原结果为例，如图6 所示，从结果观察可以看出本文方法复原图像的对比度随着迭代次数的增加有所加强，在对有活塞误差和噪声的情况下的成像图像起到了较好复原效果，相较于WF 方法减少了噪声，相较于RL 方法减少了复原后的振铃现象。

表1 不同组的子孔径活塞误差对应表Table 1 Table of piston error corresponding to sub hole diameters of different groups

图6 第一组实验结果（括号内为迭代次数）Fig.6 The first group of experimental results （iterations in parentheses）

为了得到客观的定性分析，对上述图像复原的结果使用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）、结构相似度（Structural Similarity， SSIM）［21］以及灰度平均梯度值（Grayscale Mean Gradient， GMG）进行评价。GMG 适用于无参考图的评价场景，能够较好的反映图像的边缘清晰程度和对比度的提升情况，计算首先通过Canny 算子提取边缘，在此处设置上下限阈值分别为150 和100，用来剔除与图像边缘无关的像素点，减少噪声对指标的影响，GMG 的表达式为

式中，I(x，y)表示图像的像素点灰度值。对所有组复原结果的评价指标取平均值，结果如表2 所示。从结果中可以看出，本文方法在迭代次数为8 时PSNR 和GMG 达到最优，分别为23.20 dB 和20.43，迭代次数为5 时SSIM 达到最优，为0.77，在迭代次数为3 之后三项指标的平均值均优于其余两种方法。此外，本文方法在迭代次数达到5 时，五组不同活塞误差下复原结果的评价指标方差分别为0.02、0.000 3 和0.106，均低于其余两种方法。以上说明了本文方法在有噪声以及活塞误差的情况下，能够有效的复原合成孔径系统的图像，同时具有较好的稳定性。但在耗时方面，本文方法需要更多的时间，WF 方法消耗的时间最短，仅为0.006 s。

表2 不同活塞误差图像复原评价指标平均结果（括号内为方差）Table 2 Average results of image restoration evaluation indicators for different piston errors（variance in parentheses）

进一步验证算法在多场景下图像的复原能力，共选用7 种不同场景下的遥感图像，采用此前表1 第一组的实验参数对图像进行仿真退化，复原结果如图7 所示。通过结果观察可以发现：c 组中WF 方法可以恢复图像的部分细节，但是复原过程中放大了噪声，说明了WF 方法对退化函数的设置要求较高，同时还需要较准确的噪声功率谱比值的估计。d 组中RL 算法对细节部分还原较差，存在较为明显的振铃现象，也同样产生了较为严重的噪声。e 组中本文的方法对细节部分复原较好，对噪声有较好的抑制，方法仍然存在振铃现象，但在大部分场景中相较于WF 方法有提升。客观的指标结果如表3 所示，从结果可以看出本文方法在三种指标下的结果分别为23.79 dB、0.80 和30.28，方差分别为1.91、0.001 8 和17.1，多场景下的复原结果以及稳定性上均优于其余两种方法。

表3 不同场景图像复原评价指标平均结果（括号内为方差）Table 3 Average results of image restoration evaluation indicators in different scenes (variance in parentheses)

图7 不同场景下的复原结果Fig.7 Results in different scenes

3.2 实验结果与分析

为了在实际场景中验证算法的有效性，使用合成孔径相机分别对遥感图像和真实图像进行拍摄采集，相机的合成孔径阵列结构与上述仿真一致，其余光学参数如表4 所示。遥感图像采集的方式如图8（a）所示，将高清打印的遥感图像放置在相机直线距离约110 m 处，多次更换图像一共拍摄九组，每一组包含参考相机成像和合成孔径相机成像的结果，最后对图像进行灰度化和裁切，完成图像的采集；类似的，真实图像采集的方式如图8（b）所示，拍摄真实的目标图像。

表4 相机的光学参数Table 4 Optical parameters of camera

图8 图像采集Fig.8 Image acquisition

对采集的遥感图像进行复原，实验结果如图9 所示，评价指标的平均结果如表5 所示。可以看出，在实际场景复原中，本文方法仍然能够有效地对模糊图像进行复原，提高了成像的清晰度，但对有部分细节信息无法完整地进行还原。WF 方法在图像的边缘部分会产生明显的伪影，RL 方法加强了图像的噪声。在评价指标中验证，本文方法的PSNR 和SSIM 分别达到了23.04 和0.65，相较于仿真结果没有出现明显的下降，WF 和RL 则均出现了一定程度的下降，但本文方法的GMG 结果为24.58，低于RL 方法。

表5 拍摄的遥感图像复原后评价指标的平均结果（括号内为方差）Table 5 Average results of image restoration evaluation indicators of remote sensing （variance in parentheses）

图9 拍摄的遥感图像的复原结果Fig.9 Restoration results of captured remote sensing image

最后对采集的真实场景图像进行复原，实验结果如图10 所示，评价指标结果如表6 所示。在图像中可以看出，本文方法能够对雨伞上细节有较好的还原，同时没有增加明显的噪声和伪影，评价指标结果中PSNR 和SSIM 均优于其余两种方法。

表6 拍摄的真实图像复原后评价指标结果Table 6 Results of restoration evaluation indicators of real image

图10 拍摄的真实图像的复原结果Fig.10 Restoration results of captured real image

4 结论

本文提出一种针对合成孔径光学系统退化图像的复原方法，通过将暗通道和梯度先验作为L0范数进行约束，建立复原算法模型，再使用半二次分裂法迭代求解复原的图像。在仿真实验中首先设置了多组不同活塞误差参数，评价和比较表明了本文方法在带有活塞误差的退化图像的适用性；之后设置了多组不同场景图像，本文方法在评价中具有较小的方差，验证了方法在多场景下复原的稳定性；最后进行合成孔径相机所拍摄图像的复原，本文方法的PSNR 为23.04 dB、SSIM 为0.65、GMG 为24.58，说明了方法在实际场景中的有效性。