一种基于降维密度聚类的船舶异常轨迹识别方法
李可欣,郭健,王宇君,李宗明,缪坤,陈辉
(1.信息工程大学,郑州 450001;2.32022 部队,广州 510000;3.31682 部队,兰州 730000;4.陆军特种作战学院,广西 桂林 541000;5.31438 部队,沈阳 110031)
随着经济全球化程度的不断加深,各类船舶逐渐实现高速化和大型化,持续增长的海洋运输需求与日趋饱和的航道容量之间的矛盾日益加剧,影响着海洋航运的安全与效率。为了更好地加强对海洋船舶的监控与管理,为海事监管人员提供更具针对性的解决方案,对大规模轨迹数据中的孤立、偏离、新颖数据点等进行检测。实现对海上船舶异常轨迹的识别与研究,从而实现对海域的智能高效全监控。在智慧海洋态势感知与管理方面具有重要的应用价值。
船舶自动识别系统(Automatic Identification System, AIS)包含船舶静态以及航行运动动态信息,已经成为了海上监控管理的主要数据来源。由于AIS信息最初是为避免碰撞而设计的,缺乏关于数据质量的元数据,如可靠性、确定性等,这使得利用AIS检测船舶异常成为一项非常困难的任务。AIS 数据包含地理空间特征、时序特征等一般数据所没有的特定特征,并且缺乏具有代表性的真实数据集,因此如网络流量[1]、网络安全[2]等领域的异常检测方法以及神经网络[3]、支持向量[4]等有监督模式的识别方法不适用该类数据。上述方法不仅要花费大量的时间对数据进行标记,类别不均衡也易导致检测结果的准确率降低。
针对AIS 数据特性,近年来关于海上异常检测的研究方法可以分为基于规则的异常检测[5]以及基于学习的异常检测[6]。前者通过明确定义异常行为实现对异常的检测,具有可解释性,但需要基于大量历史数据对规则进行总结,但对一些隐式规则难以发现和描述,实际可用性较低。后者基于历史数据学习一般模式中隐藏的规则,成为海上异常检测的主导方法。基于学习的异常检测方法一般可分为2个阶段:学习船舶轨迹的一般模式;检测偏离模式的偏差。在第1 阶段,以聚类分析为代表的无监督模式识别得到了广泛的应用,如K–Means 算法[7]、DBSCAN 算法[8]、OPTICS 算法[9]、CURD 算法[10],ST–DBSCAN 算法[11]、ST–OPTICS 算法[12]等。对于密度聚类通常只考虑空间信息这一问题,张春玮等[13]构建了船舶行为相似度模型,基于DBSCAN 对船舶轨迹行为模式进行识别。王永明[14]综合 K–means 和DBSCAN 算法对船舶轨迹进行聚类,以发现船舶航行轨迹异常。利用专家调查法和层次分析法对敏感水域的异常行为进行检测和排序。李楠等[15]通过聚类算法找到类簇中心点,利用轨迹信息和飞行距离构建异常因子,实现航空器异常检测。杜志强等[16]基于卡尔曼滤波,通过距离计算实现异常判别。孟祥泽等[17]采用ST–DBSCAN 算法从老年人轨迹中提取行为模式链,结合空间环境信息构建异常分析模型。冯宏祥等[18]通过船舶轨迹更新距离的均值和标准差,实现对AIS 误用等多种海上船舶异常的发现与数据处理。上述方法中聚类参数的选择往往基于经验,由于缺乏异常数据的标签,无法对所选参数的优劣进行评估,故难以获取最优参数。李文杰等[19]根据数据及自身分布特性生成候选集,基于参数寻优策略实现聚类过程的全自动化,但是在密度分布差异大的数据集上聚类效果差。万佳等[20]基于KANN–DBSCAN 方法,结合去噪衰减和多密度聚类,在实现参数自适应的前提下,提升了方法在密度分布差异大数据集上的聚类效果,但是该方法仍需设置密度阈值,且计算复杂度较高。
针对上述问题,本文提出一种基于降维密度聚类的船舶异常轨迹识别方法,将T–SNE 和自适应密度聚类结合,实现高效可靠的聚类,并根据聚类结果提取中心类簇构建类簇特征向量;最后根据不同距离阈值判别轨迹相似度,实现对异常轨迹的识别。构建海洋船舶轨迹异常模式识别模型,可以为智能海洋交通管理与优化提供科学化的数据支撑。
1 基于降维密度聚类的船舶异常轨迹识别方法
异常是指数据中不符合一般行为规范的模式。具体到海洋交通领域,异常轨迹一般包括:剧烈变速、剧烈转向、位置漂移等运动学异常以及船舶轨迹偏离一般航线、行驶在禁渔区或禁航区等规则异常。结合轨迹数据特点,设计基于自适应降维密度聚类的船舶异常轨迹识别方法如图1 所示。首先对AIS 数据进行预处理,通过随机森林分类器构建最优多维特征组合;然后通过降维密度聚类生成轨迹聚类结果;根据聚类结果计算类簇特征向量,通过计算数据集中点与特征向量的位置距离和速度角度距离,生成判断相似度检测轨迹异常的距离阈值;最后结合轨迹段航行距离评估置信度,实现对轨迹异常的检测。

图1 基于DR–DBSCAN 的轨迹异常识别分析Fig.1 Analysis of trajectory anomaly identification based on DR-DBSCAN
1.1 AIS 数据预处理
1.1.1 数据清洗
由于轨迹数据本身具有的多源异构性以及数据质量差等特点,需要对原始数据进行处理,轨迹数据处理通常需要解决以下3 个问题:过滤清洗,去除由于采样频率、采样精度、人为失误等产生的噪声数据;降低计算量;提高轨迹数据的精度。
对轨迹数据进行缺失值删除、插值等预处理操作后,对轨迹基础信息进行分析计算构建多维特征,根据MMSI 号将轨迹点分为完整轨迹段。船舶轨迹的集合M_traj、具体某一艘船舶的完整轨迹M_traji以及船舶轨迹点信息P可表示为:
式中:x、y为轨迹点经纬度信息;d为根据经纬度计算的地理空间距离;t为此段轨迹航行的总时间;v为AIS 报告的船舶速度;C为AIS 报告的船舶航向;H为AIS 报告的船舶艏向;Acal为根据H计算的角度变化;Arep为根据C计算的角度变化量;vrep为根据时间距离计算的航迹平均速度。
1.1.2 多维特征构建
数据集所选取的特征属性离散性或相异性越高,数据的聚类效果则越好。原始轨迹数据包含经纬度、航行速度、航行方向等信息。为了更充分地挖掘轨迹特征,计算轨迹的航行距离、平均航行速度、加速度、转向角等特征,避免偏离数据干扰,每个特征指标分别取平均值、最大值、最小值、中值构建轨迹特征数据集。由于特征之间也存在干扰,利用随机森林分类器对轨迹数据进行分析,对多维特征轨迹进行评估,构建最佳特征组合,避免特征间的相互干扰,提高计算精度和计算效率。
1.1.3 轨迹分段和静止点提取
停止点一般是船舶的运动状态或行为模式发生变化的点,可以反映出停泊区、捕鱼区、低速作业区等停止区域,具有重要的分析意义。从清洗后的AIS数据中提取同时满足计算速度和报告速度均为静止状态的轨迹点,构建静止轨迹点,并依据静止点对完整轨迹段进行划分。
根据保留的特征属性信息,轨迹划分的流程分为2 步:首先计算相邻轨迹点的距离、转向角以及速度;然后根据设定的速度阈值和最小轨迹长度,以静止点以及发生较大转向的点作为断点对轨迹段进行划分,筛除长度不符合要求的轨迹段,根据原始数据计算构造多维特征的时序子轨迹段特征。保留时序位置的子轨迹段集合S_traj_sequence可表示为:
对子轨迹段的多维特征进行处理,将多点二维信息转化为单点二维信息,子轨迹段特征集合S_traj_features可表示为:
1.2 降维密度聚类
1.2.1 算法原理
由于海上航行相较于陆上交通具有更高的自由度,不同海洋区域船舶航行规律具有较大差别,因此很难提前确定聚类数目。由于AIS 数据本身具有不确定性,报告数据中包含许多错误轨迹构成的噪声点,因此本文基于DBSCAN 算法,同时针对DBSCAN 算法超参数难以确定的问题,提出一种充分利用数据分布特性的基于多维特征降维的聚类方法(Dimensionality Reduction-Density-Based Spatial Clustering of Applications with Noise, DR-DBSCAN)。引入T–SNE 作为数据特征提取模块,借助多流形聚类[21]的思想,从高维数据中提取和构建更高质量和更具鲁棒性的数据特征低维有效表示。该方法的处理流程如图2 所示。
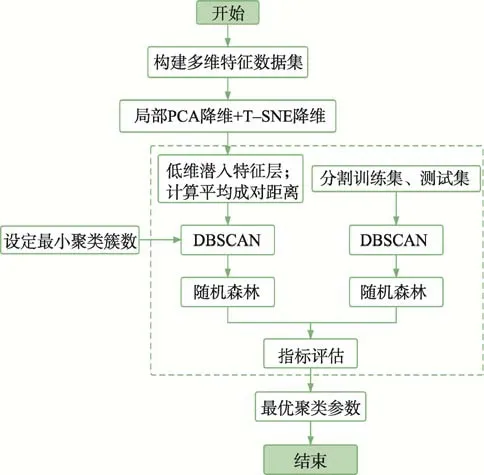
图2 DR–DBSCAN 算法流程Fig.2 DR-DBSCAN algorithm flow chart
对于多维特征数据集,常采用维数约减的方法降低特征间的复杂关系,减少噪声。常用的手段有特征删除、特征选择以及特征抽取。前2 种手段往往容易导致信息丢失,PCA 和T–SNE 都属于特征抽取的方法,在原始特征的基础上通过空间映射创建新的特征,能更好地挖掘特征间的深层联系。PCA 是一种线性降维方法,计算复杂度低但是特征表征效果较差;T–SNE 属于非线性方法,计算复杂度高但对特征映射效果较好。随机森林是一种由多个决策树组成的机器学习模型,具有很好的数据集适应能力,对高维数据、离散或连续型数据都能很好的处理,鲁棒性强。因此,本文将2 种方法结合,在提高计算效率的同时充分挖掘特征间的相关关系,使得在聚类时能充分利用数据特征间的关系;然后利用随机森林模型学习聚类标签,并判断样本类型。
在DR–DBSCAN 算法中,具体步骤如下:
1)将输入的多维特征数据通过局部PCA 方法进行投影,再利用快速T–SNE 模型将PCA 处理后的数据转化为低维嵌入。
2)计算低维嵌入层数据的平均成对距离作为eps候选集设置的基数构建候选集,并将数据划分为训练集和测试集。
3)分别将低维嵌入层数据和训练集数据代入DBSCAN 模型中进行聚类,提取集群的聚类标签,去除聚类簇数不符合设置最小聚类簇数的数据。
4)分别用嵌入层及其训练集的聚类标签训练随机森林分类器。
5)将测试集代入步骤4 中训练的2 个分类器,经过K 折交叉验证得到聚类参数最优值,输出聚类结果。
1.2.2 算法分析及评价
为了更好地验证所提出算法的性能,综合考虑内部和外部聚类评估标准构建算法评价体系。外部评价指标是指基于已知标签或模型,将聚类结果与其进行比较。选取的数据集均为有标签数据,为了对聚类结果进行准确评价,引入外部聚类指标F1分数、调整兰德系数(Adjusted Rand index,ARI)、归一化互信息(Normalized Mutual Information,NMI)作为评价指标,计算公式如下。
F1分数是精确率和召回率的调和平均数,F1越高则模型越稳健,公式见式(7)。
式中:P为精确率;R为召回率。
ARI的取值范围为[−1,1],相比兰德系数具有更高的区分度,值越大则表示聚类结果越吻合,计算式见式(8)。
式中:RI为兰德系数,取值范围为[0,1],表示聚类标签和真实标签的比值情况。
NMI值用来衡量2 个数据间的相关性,在聚类中用于度量2 个聚类结果的相近程度,NMI值越大则表示划分越准确,公式见式(9)。
式中:H(X)、H(Y)分别为聚类标签和真实标签的信息熵,即出现的概率;MI(X,Y)为互信息,是联合分布与乘积分布的相对熵。
内部评价指标是根据数据集的固有特征来对算法结果进行评估。引入聚类性能内部评价指标包含轮廓系数(Silhouette Coefficient,SC)和Davies–Boulding指数(DBI)。轮廓系数结合了凝聚度和分离度,取值为[−1, 1],其值越大越好,轮廓系数的计算式见式(10)。
式中:为a(i)簇内不相似度;b(i)为簇间不相似度。
DBI指数又称分类适确性指标,DBI越小说明聚类效果越好,计算式见式(11)。
式中:m(CI)和m(Cj)为样本间平均距离;d(μi,μj)为簇中心点距离。
1.3 船舶轨迹异常识别
1.3.1 类簇特征向量提取
在利用DR–DBSCAN 算法对轨迹进行聚类后,类簇可以代表船舶的一般运动模式。通过构建类簇特征向量来提取类簇特征,避免使用每个类簇的所有轨迹点进行计算所产生的巨大运算量,导致轨迹数据异常检测的效率降低。类簇特征向量表达式可表示为式(12)。
提取类簇特征向量表示船舶行为的一般模式,通过计算训练数据集中轨迹点与类簇特征向量的聚类距离,生成距离阈值,根据特征向量和距离阈值对测试集轨迹点进行异常检测。最后根据船舶轨迹中异常点的占比来判断轨迹段是否异常。类簇特征向量提取示意图如图3 所示。首先计算类簇平均航向角;然后根据平均航向角以及类簇点的经纬度范围构建基础网格;根据不同基础网格的经纬度跨度,将基础网格划分为小网格;计算每个网格中的类簇点的平均速度、平均经纬度、平均距离以及最大转向角;保存各个网格的特征向量,构建类簇特征向量集合。

图3 类簇特征向量提取示意图Fig.3 Feature vector extraction of class cluster
1.3.2 距离判定阈值计算
对于一个待检测的轨迹数据P,首先根据P点的经纬度坐标,利用半正矢公式计算P与类簇特征向量的地理距离Dp。
式中:R为地球半径,此处取地球平均半径R=6 371.393 km。
保留使得所求地理距离最小的类簇特征向量lGVi,根据该特征向量对应的其他特征分量计算该轨迹的相对距离d_l、速度转角距离d_sa,见式(14)—(15)。
去除噪声数据和聚类异常数据后,通过计算训练数据集中轨迹数据与类簇特征向量的距离,生成各个距离阈值,实现对异常轨迹的识别与评估。
2 船舶异常检测实验分析
2.1 实验数据
本实验选取2019 年1 月1 日的AIS 数据作为训练集,设置美国西海岸、美国东海岸和墨西哥湾3 个实验区域进行分析。
由图4 可以看出,美西和美东均分布有较多较为重要的港口,这2 个区域的客船和货船占比相对较多,分别为35.45%和28.24%。墨西哥湾北部为佛罗里达半岛,人口密度较大,该区域的船舶分布较为密集,且游艇占比较大。特殊船舶包含各种水上或水下作业船舶,如引航、搜救、挖掘、潜水等,墨西哥湾的浅大陆棚区蕴藏大量的石油和天然气,该区域特殊船舶占比较高。船舶分布与地区地理环境具有很高的相关性,根据某地区的船舶类型分布可以推论该地区的地理环境特征。
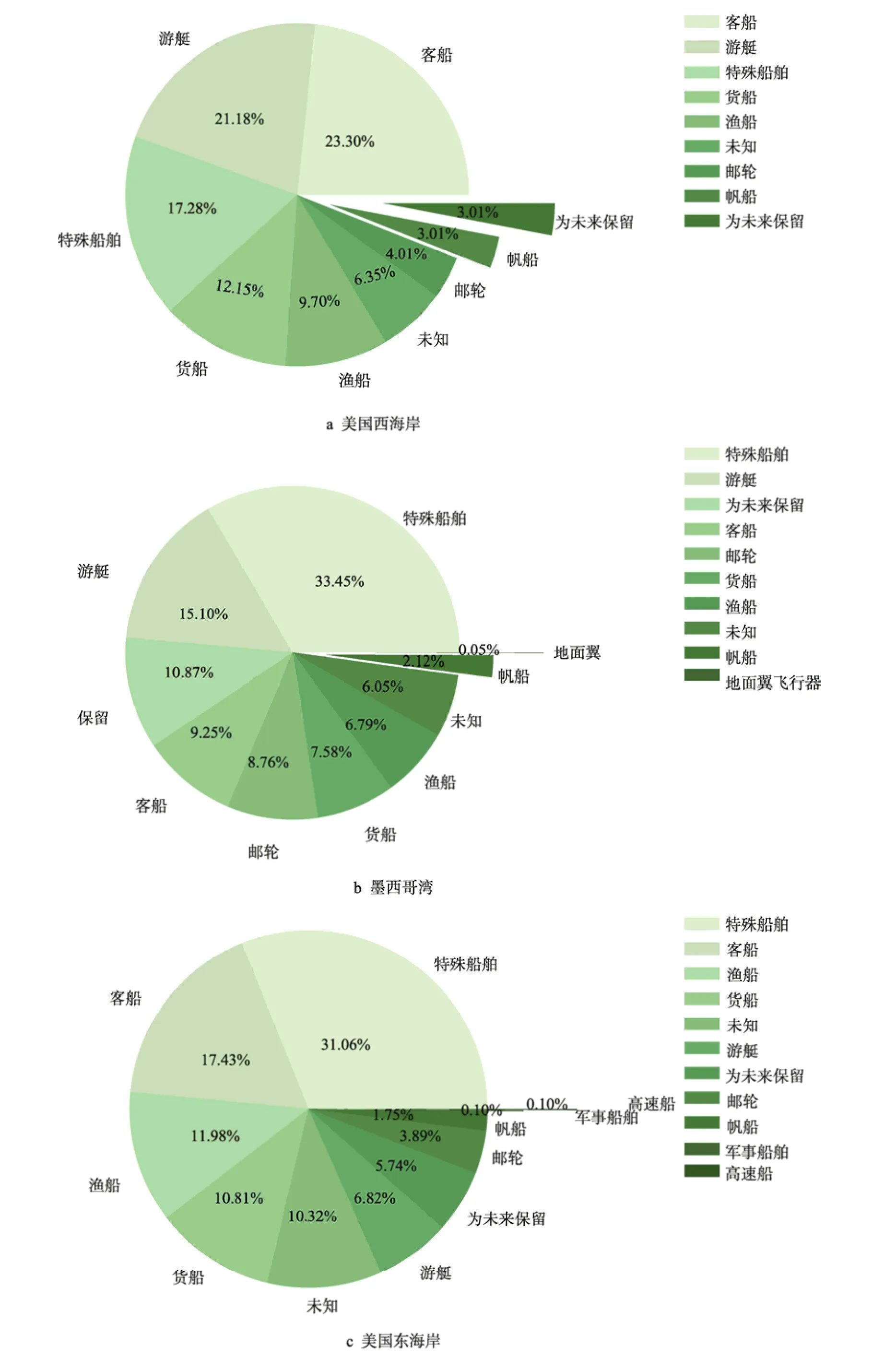
图4 实验区域船舶类型分布Fig.4 Vessel type distribution in the experimental area
2.2 数据预处理
原始AIS 轨迹数据共7 516 408 条,包含船舶13 115 艘。经过数据清洗和预处理后的AIS 轨迹数据共7 515 892 条,提取静止点615 977 个。根据设定的速度阈值筛选静止点以及航向发生重大变化的点作为断点对轨迹段进行划分,保留所有轨迹长度在10 以上的轨迹段,得到轨迹段为5 812 条,包含船舶4 740 艘。
为了确保结果的准确性与有效性,使用过滤法结合随机森林模型对特征进行组合选择,以得到最佳特征组合。进行了多组对比实验,每组实验迭代运行5次以消除随机性,实验结果如表1 所示。根据实验结果最终保留经纬度、报告转角以及报告速度的最大值、最小值、中位数和均值信息作为最终特征组合。

表1 轨迹特征组合评估Tab.1 Trajectory feature combination evaluation
2.3 聚类分析
由于轨迹数据无标签,为了验证聚类方法的精确性和普适性,选取4 个经典的具有不同维度特征的UCI 数据集进行聚类分析,评估DR–DBSCAN 算法解决实际问题的能力。综合考虑内部和外部聚类评估标准构建算法评价体系,通过属性数以及类别数的变化,观察相对变化下算法的聚类性能。数据集在不同算法下的聚类指标对比信息见表2。
从 3 个外部聚类指标F1、ARI和NMI来看,DR–DBSCAN 在4 个数据集上均有较好得分,明显优于其他几种算法,但内部聚类指标DBI评估结果相对较差。说明本文算法DR–DBSCAN 能深入挖掘数据内部特征,而不是单纯从点迹的空间分布上挖掘信息,因此能在数据分布较为离散的情况下,实现较高的分类准确度。综合实验结果分析,本文算法DR–DBSCAN 通过数据集低维嵌入特征层的构建,深入挖掘数据集特征分布特性,能够得到更符合数据特性的密度阈值。本文算法相较于一般的密度聚类方法,在实现参数自适应的同时能较好地处理多维数据集,在几个密度分布不均匀的多维数据集上均有较好的表现。
异常检测的实质就是学习一般行为模式,发现与一般模式相异的数据。DR–DBSCAN 算法能根据数据特征,拟合数据分布特性,构建数据分布一般模式的类簇,从而可以实现异常数据的识别。
在3 个试验区中,美国西海岸区域包含轨迹数据897 条;墨西哥湾区域包含轨迹2 033 条;美国东海岸区域包含轨迹数据1 027 条。根据随机森林分类器所构建的轨迹数据特征组合,对3 个实验区域的轨迹段进行聚类,去除掉无法聚类的噪声点或异常轨迹,聚类结果与船舶类型分布较为类似。根据每个区域的聚类结果,划分网格并提取类簇特征向量,计算距离阈值。3 个区域的位置距离阈值分别为美国西海岸2.249 27、墨西哥湾1.805 97、东海岸1.740 78;速度方向距离阈值分别为美国西海岸1.777 7、墨西哥湾1.952 8、东海岸1.705 02。
2.4 异常检测
根据聚类结果获取相应区域的距离阈值,将轨迹点超出阈值范围的视为异常点。对于一条轨迹,当异常点占比超过70%,则该轨迹视为异常轨迹。选取2019 年1 月1 日的AIS 数据进行异常检测,经过数据划分后,根据距离阈值判断异常轨迹点。经过距离计算和异常判定,美国西海岸轨迹数据898 条,检测出异常轨迹57 条,其中速度或方向异常速度的轨迹19 条,位置异常轨迹38 条;墨西哥湾轨迹数据2 160条,检测出异常轨迹60 条,其中速度或方向异常速度的轨迹17 条,位置异常轨迹43 条;美国东海岸轨迹数据1 054 条,检测出异常轨迹45 条,其中速度或方向异常速度的轨迹23 条,位置异常轨迹312 条。
美国西海岸和美国东海岸区域沿岸为主要航道,美西向东为内河流域,向西为大西洋;美东向西为内河流域,向东为太平洋,二者内河与沿岸区域航道明显,大洋区域轨迹较为离散。墨西哥湾区域内河流域和离港航线分布较为清晰,但在中部区域轨迹分布较为杂乱。异常检测通过计算距离阈值,将超出阈值范围的判定为异常。位置异常可以解释为分布明显偏离航道的轨迹,或同一艘船舶短时间内位置出现显著飘移等情况。将行驶方向与一般轨迹不一致或突然发生较大转向或速度变动的轨迹标记为速度方向异常;将轨迹方向与周围轨迹相异的视为方向异常;将轨迹发生较大转向的可视为转向异常。2 种方向异常都可以由轨迹分布和轨迹形状进行判断。
3 结语
本文提出了一种基于降维密度聚类的船舶异常轨迹识别方法。利用随机森林分类器对轨迹多维特征的重要性进行评估,构建轨迹特征的最优特征组合。基于DR–DBSCAN 聚类算法对历史AIS 数据进行聚类分析,学习船舶的一般行为模式构建船舶类簇特征向量并计算距离阈值。在保证聚类精度的前提下,有效提高了聚类效率,减少了调参过程中对人工的依赖。采用4 种经典UCI 数据集验证DR–DBSCAN 算法的精确度和有效性,并使用2019 年1 月1 日的真实航迹数据在3 个不同的实验区域进行分析,以减少水文地理环境对方法有效性与准确性的干扰。结果表明,该方法能够有效检测出船舶的位置异常、速度方向异常,对加强船舶交通行为分析和船舶交通监管具有重要意义。由于硬件设施限制,本文选取数据集时空范围较小,对多种类型的异常划分和定义不够详细。未来可以进一步修改模型架构在更大区域进行验证,更为明确地划分各种类型的异常,并将模型拓展至陆空交通运输领域,更好地分析判断不同的轨迹异常行为,为海陆空运输及交通管理提供数据支撑。

