基于PSO-SVM算法的空气质量分类研究

庞 曦，胡荣华，赵春生，白宁波

（1.永城煤电控股集团有限公司，城郊煤矿，河南 永城 476600；2. 中国地质大学，湖北 武汉 430074）

0 引言

目前，人们在生产生活中对空气污染的预防以及城市管理层出台治理空气污染的有关政策均是依据气象部门给予的空气污染等级，因此对空气质量等级进行精准划分对当今社会的安全发展有着重要的现实性意义[1-2]。

为了精确地对空气质量进行分类预测，很多学者对此做了深入研究。例如：邱晨提出了基于BP神经网络的空气质量模型分类研究方法[3]；常丽娜提出了基于K-均值聚类和贝叶斯判别的城市空气质量等级分类及预测方法[4]；王琛提出了哈夫曼树SVM在空气质量等级分类中的应用方法[5]等。上述方法均能对空气质量进行有效分类，但受限于算法本身的局限性，其分类效果还有待提升。例如：BP神经网络收敛速度慢，其算法精度依赖于大量的训练样本并在训练过程中极易陷入局部最优解[6]；K-均值聚类预测法需要事先给定聚类的种类数即K的取值，K值在实际应用中是难以估计的，K值偏大或者偏小都严重影响分类的精确度。本文通过分析空气质量分类的特点和现有分类方法的不足，提出了粒子群优化支持向量机算法的空气质量分类方法[7]。

选用某矿区全年在空气中测量得到的PM2.5、PM10、SO2、NO2、CO、O3数值指标组成六维输入向量，以空气质量的指标优良、轻度污染、中度污染和重度污染作为输出向量，结合PSO优化算法在分类模型训练中全局搜寻SVM的最佳参数c和gamma，然后将最佳参数应用到空气质量的分类预测中，能够大大增加分类预测的准确性。

1 SVM算法原理

SVM分为线性可分和非线性可分，其基本原理是将低维空间的样本训练数据映射到高维空间中，使得样本训练数据线性可分，进而对边界进行线性划分[8-9]。如果有样本数据：其中xi是输入指标，yi是输出指标，其分类示意图如图1所示。

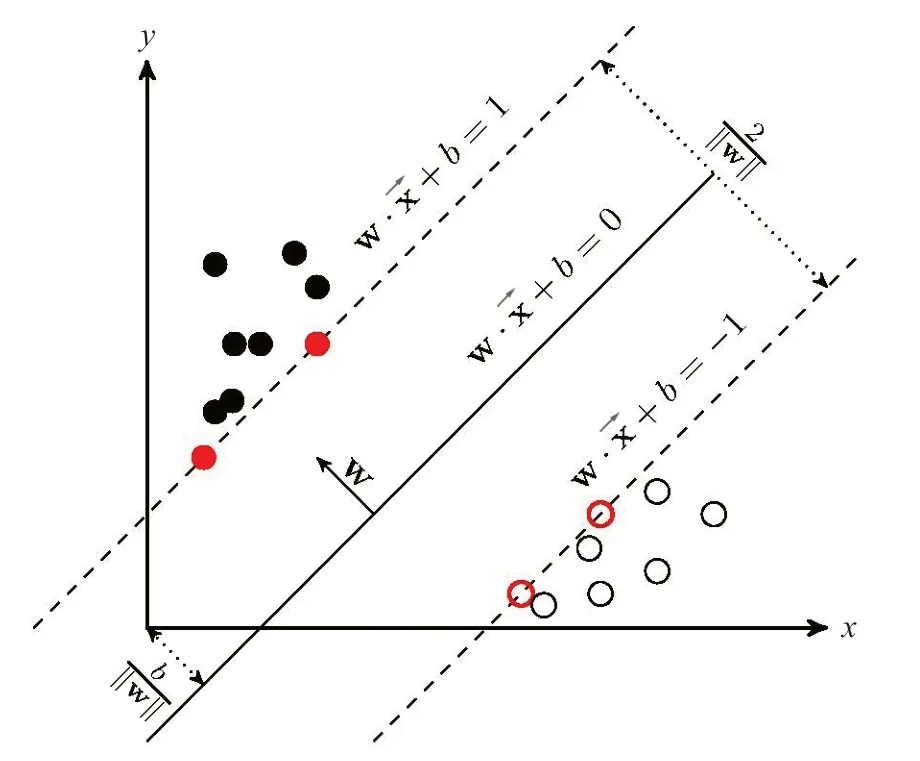
图1 SVM二分类示意图

对于二分类问题实际就是寻找区分两类数据的最优分割超平面，超平面方程如式（1）：

选择合适的w、b使距离超平面最近的样本满足得到规范化超平面，当分类间隔达到最大时确定最优超平面[10]，如式（2）：

若要使得所有样本都分类无误，根据约束条件应满足式（3）：

在式（3）中引入拉格朗日算子ai构建函数，其中ai＞0，将有约束的原始目标函数转换为无约束的拉格朗日目标函数，如式（4）：

求L对w、b的偏导，令其等于0，得到一个包含ai的函数，如式（5）：

求得w、a、b对应的最优解w*、a*、b*，获得最优分割超平面，如式（6）：

确定SVM的分类决策函数如式（7）：

2 PSO-SVM算法原理

2.1 粒子群优化算法

粒子群优化算法的本质就是迭代寻优，通过撒下的粒子种群更新其位置和运动速度在全局寻找适应度函数的最优解[11]。假设在一维目标搜索空间中，由N个粒子组成群体X的初始位置为得到初始局部最优为P1，然后更新粒子的搜寻速度和位置，在时刻t，该种群粒子更新位置至该粒子种群中局部最优位置表示为P(t)，t时刻的粒子群的局部最优位置为与初始局部最优位置相比较得到全局最优位置g(t)，然后继续迭代更新粒子的搜寻速度与位置，每更新一步都要对比得到最新的局部最优和全局最优，直至达到最大迭代次数为止。当粒子种群在M维目标搜索空间内，粒子群的速度与位置更新公式如（10-11）：

2.2 PSO-SVM算法流程

SVM在运行前需要手动设置两个参数：其中c是惩罚系数，即对误差的容忍度，c值高说明误差容忍度小，容易过拟合，c值越小容易欠拟合；gamma是核函数自带的一个参数，决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多，支持向量的个数影响训练与预测的速度[12-13]。

为了消除人为设置参数c和gamma对SVM运行的影响，使用PSO算法在全局搜寻c和gamma的最佳参数组合，具体的PSO-SVM算法流程见图2。

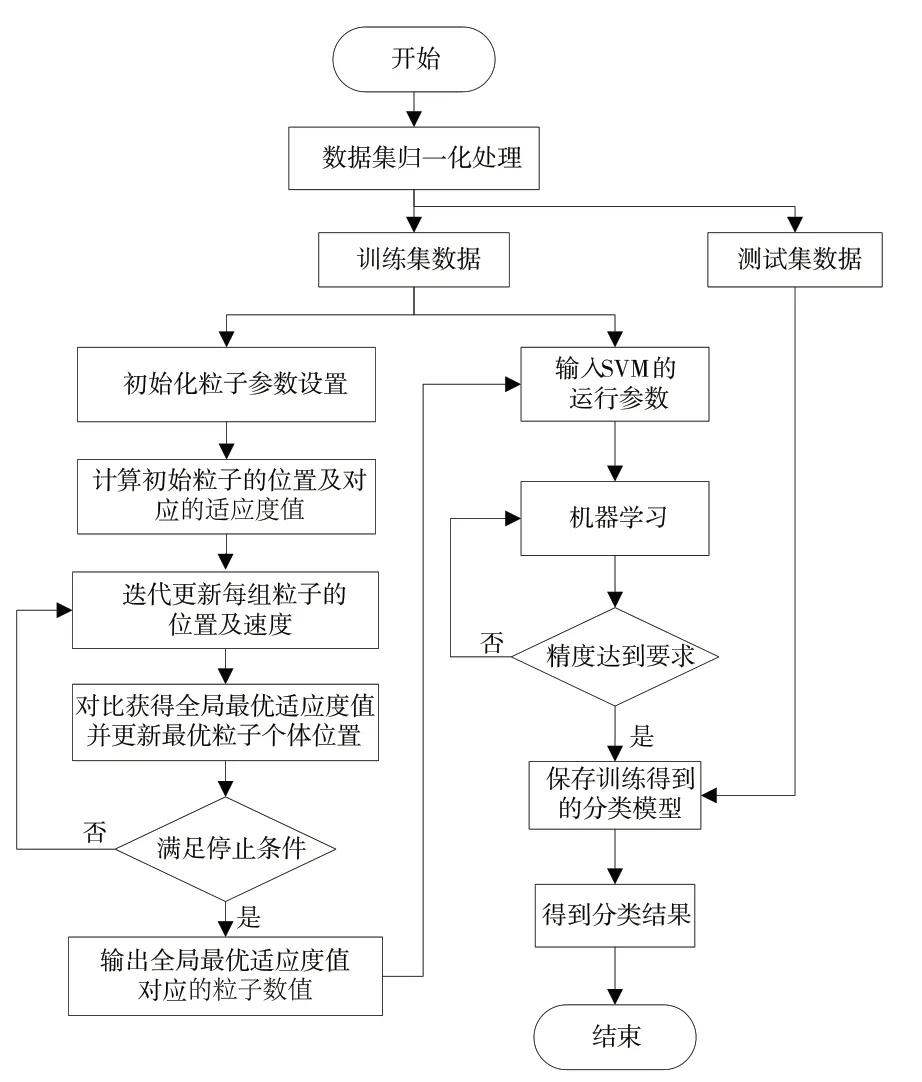
图2 PSO-SVM算法流程图

3 算例分析

选择某矿区一年度在空气中测得的PM2.5、PM10、SO2、NO2、CO、O3的数字指标组成六维输入向量，以空气质量的指标优良、轻度污染、中度污染和重度污染作为输出向量。其中优良的标签为1，轻度污染的标签为2，中度污染的标签为3，重度污染的标签为4。选择其中150组为训练数据，分别训练得到SVM分类模型、PSO-SVM分类模型，其余215组为测试数据，使用测试数据的分类准确率来评价分类模型的性能。

3.1 数据预处理

在选择输入向量的同时，为消除数据物理量纲的不同和尽量压缩数据大小的范围，以增加运行的速度，需要对数据进行归一化处理，数据归一化公式如（12）：

压缩后典型的输入、输出向量如表1所示：

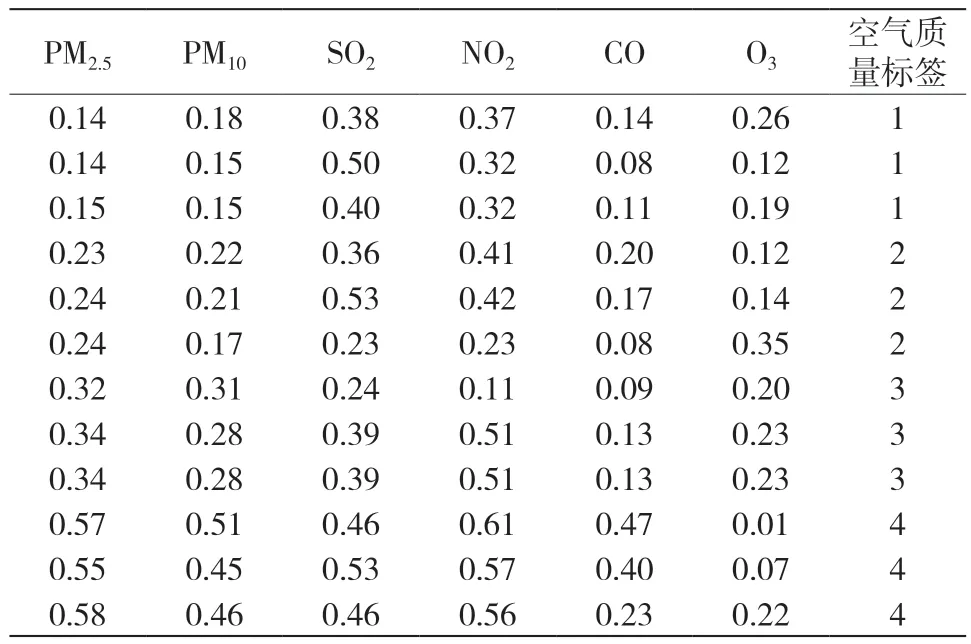
表1 几种典型的输入输出向量

从表1看出，不同空气质量之间的特征向量区别度非常大，尤其是PM2.5和PM10，随着空气质量的逐渐劣化其数值也不断增加。相比较而言，其余的特征量区分度虽然没有这么明显，但不同的空气质量所对应的数值也有着明显区别。

3.2 SVM分类模型建立

针对SVM多分类问题需要设置核函数，常用的核函数有四种，分别是线性核函数、多项式核函数、RBF核函数、sigmoid核函数。使用每个核函数训练数据都会得到不同的分类模型，然后将分类模型的输出结果与训练集数据原始标签相比较，表征四种核函数对输入数据的拟合率，拟合率越高说明此核函数越适合于此类数据的分类预测。训练数据共有150组，其中优良、轻度污染、中度污染和重度污染分别为60、60、10、20组，设置SVM的运行参数c和gamma为100和10，设置目标精度为0.001。使用4种核函数分别对训练数据集进行分类模型训练，并对分类模型的输出结果与训练集数据原始标签进行对比，得到4种核函数对应的拟合率如表2。

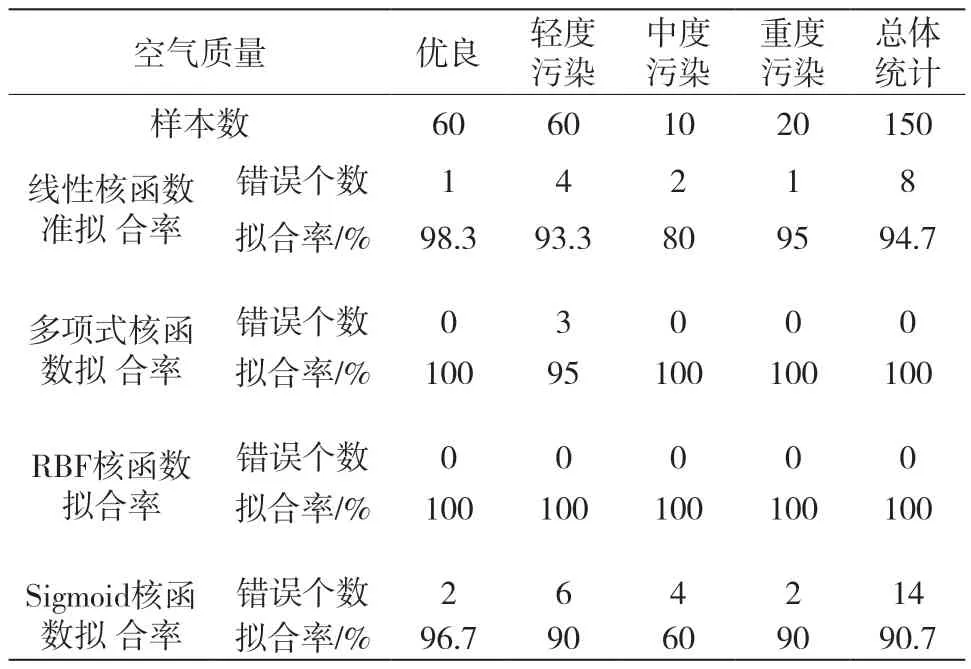
表2 4种核函数训练模型对应的准确率

从表2中的准确率可以看出，对于本次数据处理的适用性： RBF核函数＞多项式核函数＞线性核函数＞sigmoid核函数，使用RBF核函数训练得到的分类模型有着更高的拟合率，接下来的SVM分类模型均采用RBF核函数，RBF核函数公式如式（13）：

3.3 PSO-SVM分类模型建立

PSO-SVM算法的目的就是使用PSO算法在全局进行寻优，找到最佳的参数组合c和gamma，然后将最佳参数组合使用在SVM分类模型训练中，增加SVM分类模型在分类预测中的准确率，使用PSO算法需要设置一个适应度函数，作为粒子群迭代寻优的目标函数。本文采用分类预测结果与测试集数据原始标签的均方误差作为适应度函数[14-15]，均方误差如式（14）：

式中：P—分类预测结果，Y—测试集数据原始标签，length（Y）—测试集数据原始标签的长度。均方根误差值越小说明分类模型的分类预测准确率越高，PSO算法运行前需要设置算法的初始参数，设置粒子种群加速因子C1=C2=1.5、惯性权重w=0.7、粒子种群规模为20、最大迭代步数T=300、粒子搜寻空间范围为[1, 1000]，初始速度v=10，粒子群的迭代寻优过程示意如图3所示。

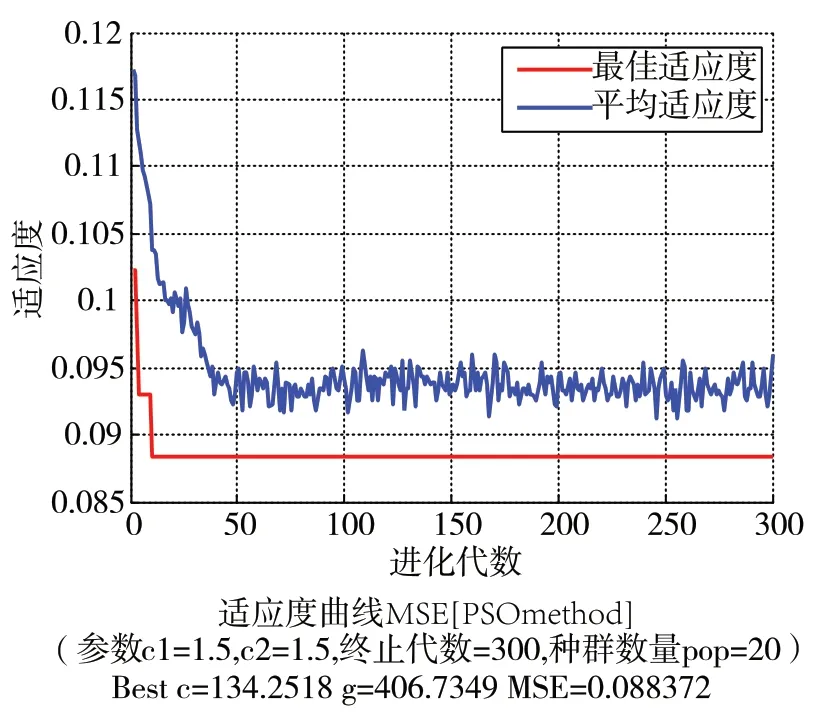
图3 粒子群迭代寻优示意图

从图3中可以看出，粒子群迭代10步之后搜寻到了适应度的全局最优值，此时MSE=0.088，c=134.25，g=406.73，每步迭代后的平均适应度值也一直逼近全局最优适应度值，说明每次迭代粒子种群都在朝着最优的位置运动。

3.4 预测结果及分析

使用SVM分类模型和PSO-SVM分类模型分别对215组测试集数据进行分类预测，其中优良、轻度污染、中度污染和重度污染分别为120、56、15、24组，分类预测结果分别如图4、图5所示。

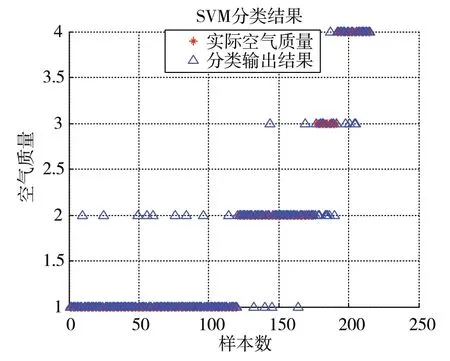
图4 SVM分类模型输出结果

图5 PSO-SVM分类模型输出结果

图4、图5显示，SVM分类模型分类正确188个样本、错误27个样本，整体分类正确率为87.44%。其中：优良样本分类正确111个，错误9个，分类正确率为91.75%；轻度污染分类正确50个，错误6个，分类正确率为89.29%；中度污染分类正确8个，错误7个，分类正确率为53.33%；重度污染分类正确20个，错误4个，分类正确率为83.33%。PSO-SVM分类模型分类正确196个样本，错误19个样本，整体分类正确率为91.16%。其中：优良样本分类正确111个，错误9个，分类正确率为91.75%；轻度污染分类正确53个，错误3个，分类正确率为94.64%；中度污染分类正确10个，错误5个，分类正确率为67.67%；重度污染分类正确22个，错误2个，分类正确率为91.67%。

从分类预测结果可以看出，PSO-SVM分类模型与SVM分类模型相比较总体分类正确率提高了3.72%，不同的空气质量样本正确率也有着较大的提高。其中：轻度污染的分类正确率提高了5.35%，中度污染的分类正确率提高了14.34%，重度污染的分类正确率提高了8.34%。

4 结论

（1）采用PM2.5、PM10、SO2、NO2、CO、O3的数值指标组成的六维特征向量，能够有效的表征空气质量的等级。

（2）通过对SVM分类算法的训练，得到的分类模型能够对空气质量等级进行分类，但是分类准确率还有待提高。

（3）PSO优化算法能够以迭代寻优的方式在全局搜寻SVM的最佳参数c和gamma，使得此时的适应度函数达到最优。

（4）PSO-SVM算法能够对空气质量等级进行分类，且相比较SVM分类算法，其分类正确率有着大幅度的提高。