基于爬虫策略的二次栅格扫描定位算法

赵正健 程良

关键词：爬虫策略；二次栅格扫描；RSSI

0 引言

伴随着互联网的快速发展，信息呈现爆炸性增长，人们在享受信息带来便利的同时也会面临如何快速定位我们需要的信息问题。当下的爬虫技术可以很好地解决此问题，给人们带来极大的便利。能否借用爬虫策略运用到现有的无线传感器网络定位中，是研究者重点关注的地方。爬虫技术的核心策略主要是在整个网络中根据自己指定的规则进行快速路由，达到提高效率的作用。无线传感器网络在定位的过程中，因为要借助传感器节点进行相互辅助定位，当这些传感器节点相互通信的时候，就牵扯到路径问题[1]。最优路径的选择将直接决定后面定位精度的大小。现有的无线网络定位算法分为两类，基于测距以及非测距[2]。对于以测距为基础的定位算法，研究者基本只在如何提高RSSI精度上纵向研究。以非测距为基础的定位算法，基本聚焦在数学公式的运用上，比如最小二乘法，加权平均等。总体来看，这两类定位技术目前比较成熟，但在精度上来说力量有限。二次栅格扫描与三角形质心定位算法目前属于较为先进的定位算法，但对于精度要求高的地方还是显得捉襟见肘。如何能够再次提高它的定位精度也是广大研究者一直在讨论的话题。所以本文提出借助爬虫策略思想，在传感器网络相互辅助通信的时候，针对各传感器节点的路由方式进行优化，得到相应的RSSI 值后再进行常规方式的优化[3]。最终来提高整体无线传感器网络的定位精度。

1 网格扫描算法

网格扫描算法整体来看可分为三步：

首先利用传感器节点随机布置网络，待定位点处于该区域中。该网络中有部分节点带有GPS功能，称为锚节点。待定位位置周围的锚节点称为邻居锚节点，最近的邻居锚节点称为最近锚节点。各个节点之间可以进行RSSI的相互通信[4]。

其次，以邻居锚节点为圆心，通信距离为半径画圆。重合区域为该未知节点所在区域。做出该重合区域的外接矩形，记为ER[5]。如图1所示。

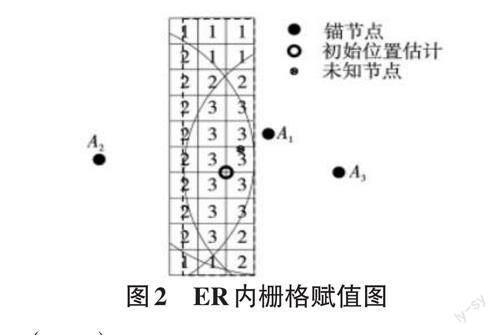
最后将该外接矩形划分成边长为l 的小矩形。若有一个邻居锚节点的通信范围覆盖到这些小格子上，则给小格子赋1，两个就赋2以此类推。最后将赋值最大的区域记为待定位区域，用Ej 表示。计算出该区域的质心可作为待定位位置坐标[6]。如图2所示。

外接矩形ER用（lx，ly）表示，（i）为锚节点的数目。（x ） i，yi 是锚节点坐标，r是通信半径。用集合G表示栅格的数目。所以外接矩形面积可用式（1）表示。集合G可用式（2）表示。

2 算法改進

2.1 爬虫策略

2.1.1 误差分析

二次栅格扫描算法的实现离不开节点之间RSSI 值的交互。通过将节点多次接收的RSSI值求平均来得到相应的距离，如式（3）。研究发现，如果一组数据中有一两个粗差存在，那么对整个实验误差是非常大的。同理，在统计RSSI值时，若将边缘节点参与计算，带来的误差也是非常大的。这里，我们采用爬虫策略，先将每个节点进行遍历一遍，设定阈值，将不符合条件的节点当作边缘节点进行舍弃。这样在原始数据上进行了一次筛选，避免了粗差带来的影响。

由于RSSI对环境较为敏感，所以当选择未知节点周围的邻居锚节点时，由于干扰的影响，距离最近的邻居锚节点所组成的区域并不一定是该未知节点真实存在的区域。针对此问题，利用爬虫策略对数据进行分析，因为三个锚节点就可以进行定位。假设在无线传感器网络中，未知节点周围有n 个锚节点，从而组成C3n种定位区域，每个定位区域的质心都可以当作未知节点的坐标。又因为该定位区中也存在锚节点，所以为了解决环境干扰，我们以定位区域的这些锚节点作为参考节点，来对比哪一组定位区域所受环境干扰最小，就选择那一组作为待定位区域，进而来进行下一步的定位工作。

上式中d为接收端与发射端的距离，d0为发射端的参考距离PL （d0 ）为距离d0时的路径损耗功率PL （d） 表示距离为d时的平均接收功率。n是当下环境的路径损耗指数。

2.1.2 CSTG-TCLLA 算法

文中提出的算法称为CSTG-TCLLA算法，具体分为三个步骤。

1） 一次位置预估

设未知节点周围存在N个锚节点，通过这几个锚节点做的通信圆形成的区域叫作首次定位区域记为Ej，通过求得该区域的质心，可当作一次定位的位置，记为S1（xt0，yt0）。

2） 优化可再定位性

对于二次栅格扫描定位主要是基于RSSI值进行的定位算法，所以对该算法精度的提高取决于RSSI值的精确性。由于RSSI值受环境因素较大，进而提高了定位过程体中精度的不稳定性，为了解决此问题，本文引入爬虫策略解决RSSI值精确性问题。使锚节点在接收未知节点发送的RSSI值的时候，避免了极端数值对实验造成的巨大误差，为后续二次栅格扫描的稳定性打下基础。

3） 栅格二次赋值

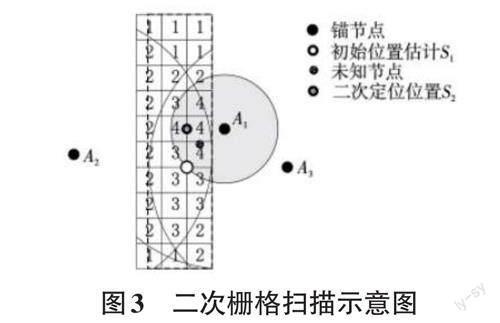
通过爬虫策略去除边缘节点之后，参与计算的RSSI值更加平滑，根据最近锚节点对未知节点进行二次扫描，扫描区域记为Ej。计算该区域中所有栅格中心到最近锚节点的距离记为D，如式（4）。

为了缩小定位区域，将集合D 中所有距离和未知节点到最近锚节点之间的距离，记为dist，进行对比。如果dm < dist，则称为可再定位区域，并且给栅格内赋值为N + 1，新的区域称为ENj，将ENj 的质心当作未知节点的坐标。如图3，若未知节点周围有三个锚节点，分别记为A1，A2，A3，以最近锚节点A1为圆心，再次扫描可得ENj区域。

3 仿真实验

3.1 实验设计

本文以Matlab为仿真环境，通过随机拓扑节点的方式来模拟现实环境中的定位场景。给定部分节点固定的位置坐标以及未知节点的坐标。通过定位算法定位出未知节点坐标，进而与给定的未知节点坐标做对比，以此来衡量不同算法的误差程度。文中所提出的新算法记为CSTG-TCLLA算法，传统的二次栅格扫描算法，二次栅格扫描算法以及文献[4]中的算法分别记为TGTCL-LA算法，Grid-scan算法和VGrid-scan 算法。利用式（4）计算每种算法的定位误差，并且将从通信半径，节点个数，锚节点个数以及栅格边长这4种情况下充分来比较几种算法的定位精度。

E为平均误差，（xr，yr），（xt，yt）分别为未知节点的估计坐标和未知节点的真实坐标，k为拓扑次数，nr 参与定位的未知节点个数。

3.2 通信半径对定位误差的影响

为了验证通信半径的不同对定位误差的影响，实验中选取固定的节点个数200个，以及锚节点个数30 个，规定小格子的长度为2米，以此来进行仿真实验，结果如图4所示。

由实验结果得，对比较为流行的这几种算法。CSTG-TCLLA算法与TG-TCLLA算法，VGrid-scan算法以及Grid-scan算法相比，平均定位误差分别减少了7.2%，10.68%以及12.83%。

3.3 节点个数对定位误差的影响

同理为了测验节点个数对算法精度的影响，控制其他量都不变的情况下，改变节点个数的数量，对比这几种算法的定位误差，仿真图如图5所示。

由图5可得，给定节点个数为N、锚节点个数为0.3N、通信半径为20米、栅格边长为2米。文中提出的算法相比于Grid-scan算法、VGrid-Scan算法以及TG-TCLLA 算法，在平均定位誤差上分别减少了13.62%、11.58%以及9.26%。

3.4 锚节点个数对定位误差的影响

给定节点总数为200个，通信半径为20米，栅格长2米，分析几种算法的定位误差，如图6所示。

仿真可得，文中提出的算法相比于传统的Gridscan算法、VGrid-Scan 算法以及TG-TCLLA 算法，在平均定位误差上分别减少了11.2%，5.8%以及3.6%。

3.5 栅格边长对定位误差的影响

规定节点个数为200，通信半径为20米，锚节点为30个，仿真结果如图7所示。

由仿真图可得，栅格边长的大小也是影响定位算法误差的主要因素。文中提到的算法相比较于传统的Grid-scan算法、VGrid-Scan算法和TG-TCLLA算法在定位误差上分别减少了8.26%，6.24%以及2.68%。

4 结束语

二次栅格扫描算法主要依靠节点间RSSI值的大小关系进行相关定位计算。由于RSSI值受环境因素影响明显，常规处理方式通过求平均或采用卡尔曼滤波算法来平滑RSSI值。但并不能避免RSSI粗差带来的影响。同时在具体定位过程中，多径效应的影响使得距离最近的锚节点所组成的定位区域并不一定是未知节点所在区域，从而造成定位误差。本文采用爬虫策略解不仅舍弃边缘节点，而且在最终的定位区域选择上，借助已知锚节点的位置，进行了客观上的对比，选择出最优的定位区域。从而系统性地提高定位精度，改进了二次栅格扫描算法。