一种具有边缘保持的去除图像椒盐噪声算法
许超 李月月 陈初侠

关键词:边缘保持;椒盐噪声;标准差;峰值信噪比
0 引言
椒盐噪声是图像滤波中常遇到的一种噪声,会严重影响图像的质量,也会对图像的后续处理如图像分割、特征提取等产生不良影响。所以,去除图像中的椒盐噪声具有很大研究价值[1]。
常见的邊缘保持类滤波算法有四种,分别是灰度最小方差均值滤波器(Gray Minimum Variance MeanFilter,MVM)、K 近邻平滑滤波器(K-Nearest NeighborSmoothing Filter,KNN)、对称近邻均值滤波器(Symmet?ric Nearest Neighbor Mean Filtering,SNN) 和西戈玛平滑滤波器(Sigma Smoothing Filter,SSF) [2]。在去除椒盐噪声方面,最有效的算法是中值滤波(Median Filter?ing,MED) 。以上五种算法中,MVM去噪能力强,但保留图像边缘细节能力弱;KNN保持边缘能力较强,但算法复杂,计算量大;SNN虽然能保持边缘,但随着噪声密度的增大,效果越来越差[3];SSF去噪能力强,但会使图像变模糊;MED算法虽然在一定程度上能改善图像的模糊,但滤波后图像模糊的事实依然存在[4]。
为了在噪声密度较大的情况下,能有效地去除图像中的椒盐噪声,并保持图像的边缘细节[4],本文借鉴KNN、SSF和MED算法,提出一种新的具有边缘保持的去除图像椒盐噪声算法(Keep the Boundary Filter,KBF) 。该算法的基本思想是:1) 首先判断像素点是否为噪声点;2) 对于非噪声点,先与模板中像素的中值进行比较,若两者之差的绝对值大于25,则输出为中值,否则输出像素本身;3) 对于噪声点,先与模板中像素的中值进行比较,若两者之差的绝对值大于25,则输出为中值,否则输出为与中心像素灰度值最接近的9个数的均值。
1 本文算法原理
为了更好地保留图像的边缘细节信息,本算法的核心分两步走,一是判断噪声点;二是对噪声点和非噪声进行处理。下面分别对它们进行详细的阐述。
1.1 噪声判断
噪声判断是本算法很关键的一步,因为是否能准确判断出噪声点关系到所有噪声能否被完美滤除。
若不能判断出噪声点,必然导致滤波后的图像仍然含有噪声点,滤波效果不完美。本文借鉴SSF 算法思想,来判断图像中像素是否为噪声点,判断方法如下。
1) 以待处理像素f(x,y)为中心[5],构造5×5的模板。
2) 计算模板中的像素标准差s。
3) 如果f(i,j)-2s≤f(x,y)≤f(i,j)+2s,则δ(i,j)=1,否则δ(i,j)=0。其中,f(i,j)为像素点(i,j)的灰度值,f(x,y)为模板的中心像素值。
4) 若模板中δ(i,j)=1的像素个数大于P(P一般取3) ,则中心像素f(x,y)为非噪声点,反之为噪声点。
1.2 图像滤波
滤波过程中,需要对噪声点和非噪声点作不同的处理。本文在借鉴KNN和MED算法的基础上,确定图像滤波方法,步骤如下。
1) 以待处理像素f(x,y)为中心,构造5×5的模板。
2) 计算5×5模板中像素灰度值的中值,设为median。
3) 对于非噪声点,若| f(x,y)-median |>25,则输出为median,否则输出为像素灰度值本身f(x,y)。
4) 对于噪声点,若| f(x,y)-median |>25,则输出为median,否则输出为与中心像素灰度值f(x,y)最接近的9个数的均值。
1.3 算法具体步骤
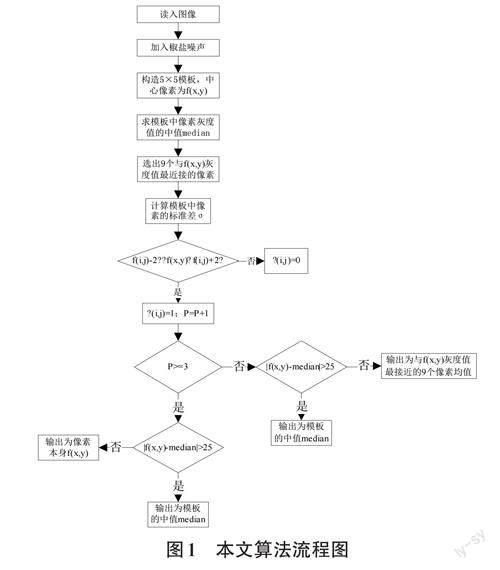
通过以上噪声滤波算法可知,图像在含有椒盐噪声的情况下,先判断噪声点,再进行滤波处理,能有效去除图像中的噪声点。结合噪声判断和图像滤波,本文算法的具体步骤如下。
1) 读入图像并对图像添加椒盐噪声。
2) 以待处理像素f(x,y)为中心,构造5×5的模板。
3) 计算5×5模板中像素灰度值的中值,设为median。
4) 选出9个与f(x,y)灰度值最接近的像素。
5) 计算模板中的像素标准差s。
6) 判断待处理像素是否为噪声点。
①如果f(i,j)-2s≤f(x,y)≤f(i,j)+2s,则δ(i,j)=1,否则δ(i,j)=0。其中,f(i,j)为像素点(i,j)的灰度值,f(x,y)为模板的中心像素值。
②若模板中δ(i,j)=1的像素个数大于P(P一般取3) ,则中心像素f(x,y)为非噪声点,反之为噪声点。
7) 若f(x,y)为非噪声点,先把它与median进行比较,若两者之差的绝对值大于25,则输出为median,否则输出为f(x,y)。
8) 若f(x,y)为噪声点,先把它与median进行比较,若两者之差的绝对值大于25,则输出为median,否则输出为与中心像素灰度值最接近的9个数的均值。
本文算法流程图如图1所示。
2 实验结果与分析
为了验证本文算法的有效性[6],将其与MVM、KNN、SNN、SSF、MED五种算法进行对比。首先对图像添加不同密度的椒盐噪声,然后用六种算法对不同噪声密度的图像进行滤波处理,最后从主观视觉和客观评估指标对不同算法的性能进行评价。
2.1 主观评价
为了对六种算法的性能进行全面的比较,笔者对原始图像添加了13种密度的椒盐噪声,噪声密度从1%增加到30%。为展示方便,这里只展示出四种噪声密度的滤波情况。图2为原始图像及添加椒盐噪声后的图像(噪声密度为0.05、0.1、0.2、0.3) ,图3、图4、图5、图6 为六种算法对不同噪声密度图像的滤波结果。
从图3至图6可以看出,传统的四种边缘保持类滤波算法虽然对图像的细节进行了有效保护,但随着噪声密度的增大,滤波后的像素灰度值与原始像素灰度值的差值也变大,图像变得不清晰,而且出现不能有效滤波噪声的现象。传统中值滤波能有效去除噪声噪,但在平滑噪声的同时,模糊了图像的边缘和细节信息[7],不能很好地保持边缘,这是因为它对每个像素进行处理时,没有受椒盐噪声污染的像素也被中值代替。相较于前面五种算法,本文算法无论在什么噪声密度情况下,其滤波后的图像明显更清晰,更接近原图像,即使噪声密度增大,它也能有效滤除噪声,并很好地保留图像边缘信息。
2.2 客观评价
除上述主观评价外,本文还采用峰值信噪比(Peak Signal to Noise Ratio,PSNR) [8]对图像滤波的效果进行客观评价。通过对参数的对比,能更客观地比较出差异。PSNR(单位:dB) 可反映图像的噪声水平,其数值越大,表示滤波后的图像越接近原图像,去噪能力越强,其定义表达式如下:
式(1) 中,xi,j为原始图像,yi,j为滤波后图像,M×N 为图像的大小。
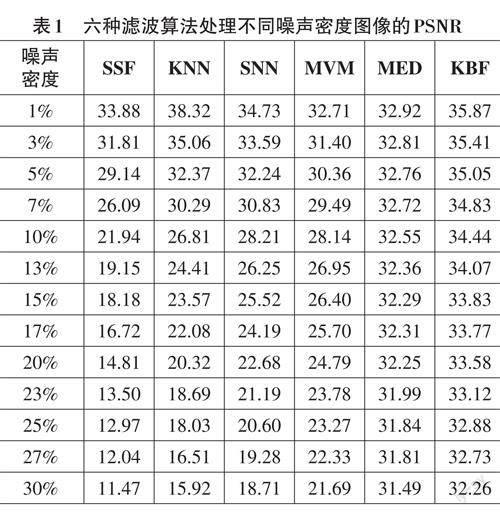
表1为MVM、KNN、SNN、SSF、MED、KBF六种滤波算法处理不同噪声密度图像的PSNR数值。从表1 中可以看出,只有在1% 密度的噪声下,KNN 算法PSNR的数值大于KBF算法的数值,在其他密度的噪声下,随着噪声密度的增大,KBF算法PSNR的数值远大于传统的四种边缘保持类滤波算法和传统的中值滤波算法。这说明KBF算法滤波后的图像更加接近原始图像[9],对椒盐噪声图像具有更好的去噪能力和细节保护能力[10]。
3 结束语
本文在MVM、KNN、SNN、SSF、MED算法的基础上,提出了一种具有边缘保持的去除椒盐噪声算法,该算法首先对噪声图像进行噪声点的判断,然后对非噪声点和噪声点做不同处理。实验结果表明,该算法比以上五种算法对椒盐噪声图像的处理有更好的去噪能力和边缘保持效果。

