三个方面指向核心素养下的小学数学创生课堂

李娟

当今教育培养的人才究竟应具备什么样的核心素质，才能适应21世纪社会发展的需要？各经济体一致认为21世纪每个学生必须掌握的核心能力和技能包括：批判性思维、创新能力、分析和解决问题能力、终身学习、团队合作、自我管理和自学能力等。研究表明，创新能力并非少数人才具备的特殊才能，而是绝大多数人都拥有的潜能，通过教育为人才的创造力培养奠定基础，不仅是重要的，而且是可能的。正因为如此，从小学阶段就开始注重培养人的创新能力，既是国家意志，也是行业规则。

“双减政策”的显然要求，课程标准的已然规定，教学变革的应然需要，核心素养教育的实然走向，课堂变革是必然趋势。我们致力于核心素养下的小学数学创生课堂实践研究，旨在以学生为本，培养学生的创新思维，让每个学生的生长在课堂中真实发生。

一、聚焦核心素养，定位学习目标

实施2022年版义务教育数学课程标准，让数学核心素养落地，先从定位每一堂课的学习目标开始。学习目标是整节课的“大脑”，正确定位学习目标，有助于明晰课堂方向和学生学习导向。按照2022年版义务教育课程方案的提法，就要引导学生在增长知识、见识上下功夫，就是知识、见识并重，以学习目标引导课堂教学，从单纯关注知识技能向知识见识并重发展，向关注智慧的增长幅度和智慧的教育效果发展。

首先，目标体现学生的主体地位。目标的表述不再是“教学目标”，而是“学习目标”。教学目标的表述方式，仍然以教师的教为主，侧重于教师怎么教，学生千丝万缕的思绪，仍然被教师的教所牵引。而学习目标的表述方式，明确以学生的学为中心，侧重于学生怎么学，教师为学生的学习铺路、搭桥、引导、辅助。如，“鸡兔同笼复习课”学习目标：让学生总结归纳鸡兔同笼问题的解题步骤。这个目标中“让”这个动词，清楚明白地把教师摆在了主体地位，谁让学生总结，当然是教师让学生总结，学生被动参与，没有体现学生的主体地位，绝不能保留“让”这个动词。调整后的学习目标：1.通过复习，能熟练应用假设法解决生活中有关鸡兔同笼问题。2.归纳总结用假设法列式计算的解题步骤，进一步巩固“鸡兔同笼”问题的数学模型。

其次，学习目标育人化。2022年版数学课程标准要求充分体现学科育人的功能，学习目标必须指向三会、培养四基、发展四能，明确学习结果所要达到的程度。学习的育人功能，在学习目标中，在师生的对话中，在生生互动、合作交流中，在学习的全过程中。所以，在上面调整后的学习目标基础上，增加学习目标：3.增强学生的理解应用能力，培养学生独立思考、自主探究的意识。4.经历解决问题的过程，体验解决问题方法优化的数学思想，体会数学知识在生活中的广泛应用。

二、对标核心素养，创生课堂教学

1.情境激趣，留白引思

无论是在课堂导入，或是在探究学习，还是在巩固练习环节，都要为学生的学习设置一个接近学生生活的真实情境，既能激发学生的学习兴趣，又能最大限度调动学生的学习积极性。世界上有很多现实情境，可并不是所有的情境都接近学生们的生活，无论是数学的眼光、数学的思维，还是数学的语言，它们都是我们在同现实世界打交道的过程中形成的，因此要以同理心明晰设计真实的情镜。

如，在六年级下学期“人民币单位的总复习”时，在课堂导入这一环节，设置张同学和爸爸妈妈一起为新居选购新床的情境，可以播放一段超市购买新床的小视频，视频中要有張同学一家的所说、所做、所想、所感。所说，包括张同学一家围绕床价格的争论、不同款式床价格的比较等；所做，包括张同学一家做了哪些事，有哪些行为？学生必须要认真仔细地观察视频中张同学一家的所说和所做，才能深刻感受到张同学一家所担忧的价格困扰已成为他们家购买新床的痛点。进而学生才能把自己置身真实情境中，推测张同学一家的所想、所感，最终目的是要推测出张同学一家的价值取向和真正关心的价格问题，张同学一家的期待就是物美价廉，从而聚焦到价格上，也就在学生兴致勃勃的观察、讨论、推测中，激活学生的生活经验，自然而然地引入人民币单位的总复习课。

2.任务驱动，思辨培能

培养创新型人才，要从基础教育抓起。数学是一门训练思维的学科，好的数学课堂就是能够发展学生思维的课堂，数学教学的本质就是发展数学思维，将思维训练和创新精神贯穿在小学数学教学中，让学生获得聪明才智与创新思维能力。传统的数学课堂是一种生搬硬套的模式，学生是被动的倾听者、接受者。学习注意力集中在知识要点，相对缺少开发人的独立和批判性思维的能力，思辨能力相对狭窄。小学数学课堂教学，一定要重视培养学生的思辨能力。在任务驱动下，培养学生主动树立自己的观点与其他同学进行辩论，或者对于自己的观点进行修正。因此教师要鼓励学生进行主动地思维，让学生主动挑战高阶思维问题，主动质疑小组成员，甚至质疑教师，采取互动的方法，在思辨中，进行启发式、探究式、参与式学习。

弗莱登塔尔说：“学数学，就是要在做中学”。“明辨笃行”，故我们提倡“玩中学”。如，教学“一年级加法的复习”一课时，传统的复习课就是把这些算式展示出来，让学生们观察，你能发现什么规律？而且一年级加法算式那么多，都呈现出来，想要发现规律，对于一年级的学生来说，难度太大。教师给他们一个问题，学生们10分钟之后，仍然各自做各自的，各自说各自的，他们也不会去观察。因此，教师要改变教学方式，以游戏活动为载体，激发学习动力。让学生通过摆一摆、放一放，发现这些规律，从而提升学生们的思维水平。教学中，教师必须要给学生提供分析支架，助力学生进行分析，寻找规律。对于一年级的学生，教师一定要把书中静态的算式变成一个动态的加法表，把每一张算是卡片交到孩子手里，设计一个邮递员送信的游戏，把课堂还给学生，让学生扮演小小邮递员，信件就是每一张算式卡片，每一个邮箱上的号码就是加法算式的和，任务就是让小小邮递员把算式卡片送到对应的邮箱里，每一张算式卡片由学生们一张一张地往邮箱后面贴上去。小邮差们送信粘贴的过程，一定要经历一个从无序到有序的过程，允许学生送错信，在试错中、经历中，他就能形成经验，不再出错。教师不能急于求成，让学生们在互相的交流过程中，互相引导、帮助，悟出规律，让学生自主调整贴错的卡片。而且在同一个邮递员送信游戏中，每个环节又应该有不同的目标，比如说1号和2号信箱要让学生们巩固加法的意义；3号和4号信箱，关键要抓住学生生成的资源，促使学生从跟着做转变为探究学；5号和6号信箱要让学生学会多种的观察角度；7号、8号、9号信箱就要故意把个别算式卡片藏起来，让学生思考、补充、口述丢失的算式卡片中的算式是什么？补充这张算式卡片的理由是什么？以此强化规律，用一种逆向思维来培养学生们的思辨能力。

游戏促学、活动培能，在出错、纠错、认知冲突中引发思辨，培养创新思维能力。邮递员送信的活动，就是在任务驱动下，学生主动参与学习，在思考、讨论、借鉴、修正过程中，培养问题的发现者、提出者、思考者和解决者，不是加法表规律的被动接受者，也不是机械记忆的追随者。借助经验自主建构，实现真正意义上的深度学习，使记忆轻松，了解深刻。

3.尊重差异，求联迁移

无论是在信息技术助力的数学课堂，还是在常规的课堂学习中，教师都要尊重学生数学表达的差异，这样才能促进学生个性化学习，有助于培养学生的创新思维能力。留给学生充足的时间，让学生在不同数学表达的比较中求联，在求联中迁移，把数学知识迁移到生活应用中去。构建生生皆学、处处能学、时时可学的高质量个性化学习体系。在数学表达差异中培育“跨差异、求融通”的学习共同体，实现合作式、探究式学习与个性化培养的有机结合。学生在不同的数学表达方式中，展现不同的思维路径。在交流思考过程中，跟进练习，夯实数学知识点、算理算法，理清内在逻辑，深挖通性通法。在不同的思维碰撞中，拓展解题的思路，尊重不同的数学表达，把不同的方法勾联、融通、迁移，提高学生解决问题的能力。

如，教學“除数是一位数除法的复习课”时，设计这样的练习：张老师在体育商品店买了4个小球和1个大球，共花了26元。大球小球的单价都是整元数。而且，大球的单价比小球的单价稍贵一点点。小朋友，你知道大球和小球的单价各多少元吗？学习过程中，教师一定要鼓励学生用自己最喜欢的方法解决问题，最后展示出学生不同的计算方法。

方法一：假设法，先假设全是小球，再列式26÷（4+1）=5（元）……1（元），计算出小球的单价，接着列式5+1=6（元）计算出大球的单价，最后检验。可以设计问题串如下：

1.小球的数量有几个？

2.大球的数量有几个？

3.小球和大球一共有几个？

4.为什么可以假设全是小球呢？（即：假设大球和小球的单价一样）

5.为什么可以把大球、小球的数量合并起来？

......

在问题串的驱动下，学生小组合作、讨论、交流、梳理出：

1.“小球的价格+大球的价格=总共的价格、小球的数量+大球的数量=球的总数量”这2个基本的等量关系。

2.既然是假设法，既可以把大球假设为小球，也可以把小球假设为大球，因为我们的小球更多一些，如果把所有的球都假设为大球，那么，总价钱就会大于26元，基于本题的已知条件，不便于推理和用算术法计算，就给自己的计算设置了障碍，故假设为小球更合理一些。

3.剩余的“1元”，一定是大球和小球的单价差，因为题目中说得很清楚，大球的单价比小球的单价稍贵一点点。

方法二：列表枚举，紧扣已知信息“4个小球和1个大球，一共花了26元”“大球的单价比小球的单价贵一点点”，进行列表枚举，小球的单价最低是“1元”，小球的单价最高是“5元”，可以推理得到小球的单价是5元，大球的单价是6元，即1个大球比1个小球多“1元”。

鼓励学生尝试多种方法，尊重数学表达方式的差异，真正实现深度学习。学生在分析、理解、思辨过程中，质疑问难，提升思考。在思辨深化后，还要鼓励学生调整自己的方法，研究他人的方法。并且在比较中求联，寻求解决问题的最优方法。

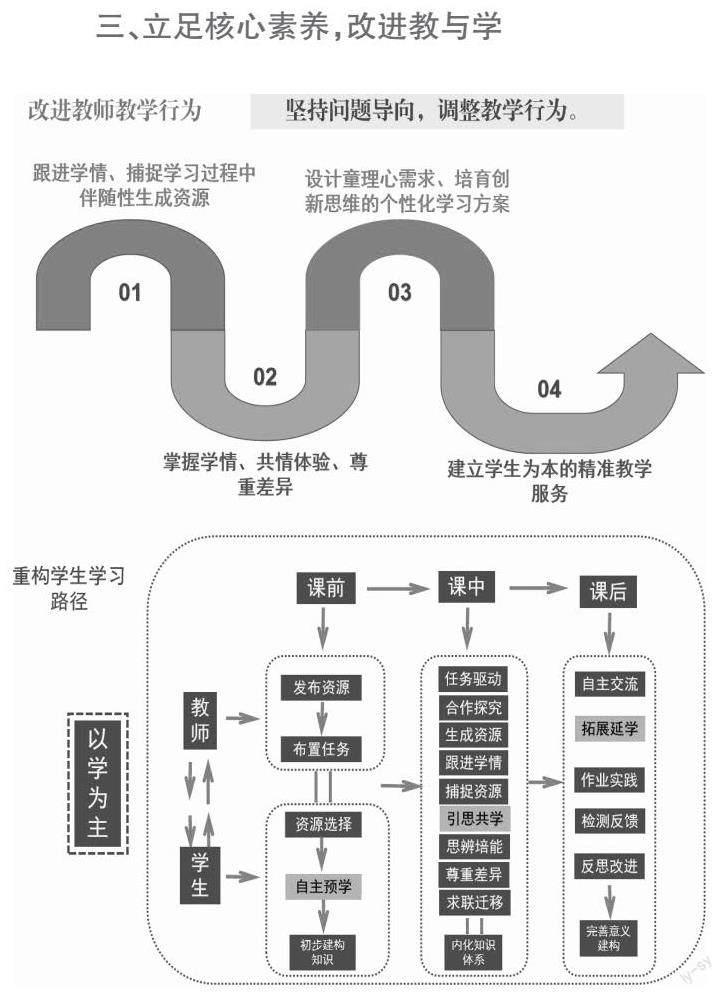
三、立足核心素养，改进教与学