气隙磁密3次谐波对电机振动噪声的影响

乔鸣忠,卢希浩,张 弛

(海军工程大学 电气工程学院, 湖北 武汉 430033)

电机是舰艇上的重要设备,不仅数量多,而且应用频繁。电机的振动和噪声对于舰艇的隐身性能及其船员生命力的保障极其重要,因此降低电机的振动和噪声是一项十分重要的课题。

电机的噪声包括电磁噪声、空气动力噪声和机械噪声,其中电磁噪声是最主要的噪声源[1]。国内外对电机电磁振动的研究方法主要有解析法、有限元法和实验法[2]。解析法建立了电机气隙磁密以及径向力波的数学模型,能够方便地计算电机所受到的电磁力,并且通过弹性力学方程求解定子的振动变形情况。但采用解析法会简化很多实际条件,使得计算结果不够准确。在解析法的基础上,有限元法为求解电机的振动噪声提供了新的工具。采用有限元法能够准确得到电机的气隙磁密及电磁力波分布,并且可以查看各个频率下的振动和噪声响应,但有限元法并不能代替解析法对电机的振动噪声进行理论性分析。在进行电机的振动噪声计算时,一般采用两者结合的方式[3-5]。

在进行普通的电机设计时,通常希望电机的气隙磁密有较高的正弦性,以降低电机的转矩脉动和电机损耗。在设计低噪声电机或者进行电机的优化设计时,很多研究学者采取了同样的思路。文献[6]进行了转子结构和绕组排布两个方面的设计,提高了电机气隙磁场的正弦性,降低了电机的电磁振动噪声。文献[7]优化了转子隔磁桥结构,使得各阶气隙磁密的幅值下降,提高了气隙磁密的正弦性,同时也改善了电机的振动噪声。文献[8]以气隙磁密谐波畸变率指标为设计依据来设计低噪声电机,实验结果表明,其设计方案能够有效降低电机振动噪声。虽然文献[6-8]均降低了电机的振动噪声,但是没有相关的理论证明提高气隙磁密的正弦性一定能降低电机的振动和噪声。

基于以上分析,本文以一台11 kW的Halbach转子结构电机为研究对象,在解析法的基础上通过排出力波表的形式,确定了引起电机振动和噪声的主要力波频率和阶次。为了说明电机振动噪声与其气隙磁密正弦性无负相关关系,本文将该Halbach结构永磁电机与一台参数基本相同的径向充磁结构的永磁同步电机作对比,发现了气隙正弦性好而振动噪声大的现象。为了探究气隙磁密3次谐波对电机振动噪声的函数关系,本文建立了Halbach结构电机的气隙磁密及径向力波的数学模型,并通过遗传算法求解了电机气隙磁密3次谐波的最佳幅值。

1 电磁力计算及分析

1.1 气隙磁密表达式及其拟合函数

电机的气隙磁密主要是径向磁密,切向气隙磁密幅值很小[9],忽略切向磁密,转子磁势的表达式为:

(1)

式中:μ为μ/p次磁势谐波的极对数,ω1为基波电角频率,θ为空间角度。

考虑转子凸极和定子开槽,气隙长度为δ时的磁导为:

(2)

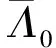
则同步电机空载时的气隙磁密表达式为:

bμ(θ,t)=f(θ,t)λ(θ,t)

(3)

将式(1)和式(2)代入式(3)中,即可得到空载时具体的气隙磁密表达式。

电机负载时,定子绕组通入对称的三相正弦电流,所产生的电枢反应磁场为:

(4)

将式(3)和式(4)相加,即可得到电机负载时的气隙磁密表达式:

b(θ,t)=bμ(θ,t)+bv(θ,t)

vθ-(φ+90°)]

(5)

以一台舰艇用机泵一体化电机为计算目标,该电机是一台Halbach转子结构20极24槽的永磁同步电机,额定运行功率为11 kW,额定转速为1 000 r/min,电机的截面图如图1所示。

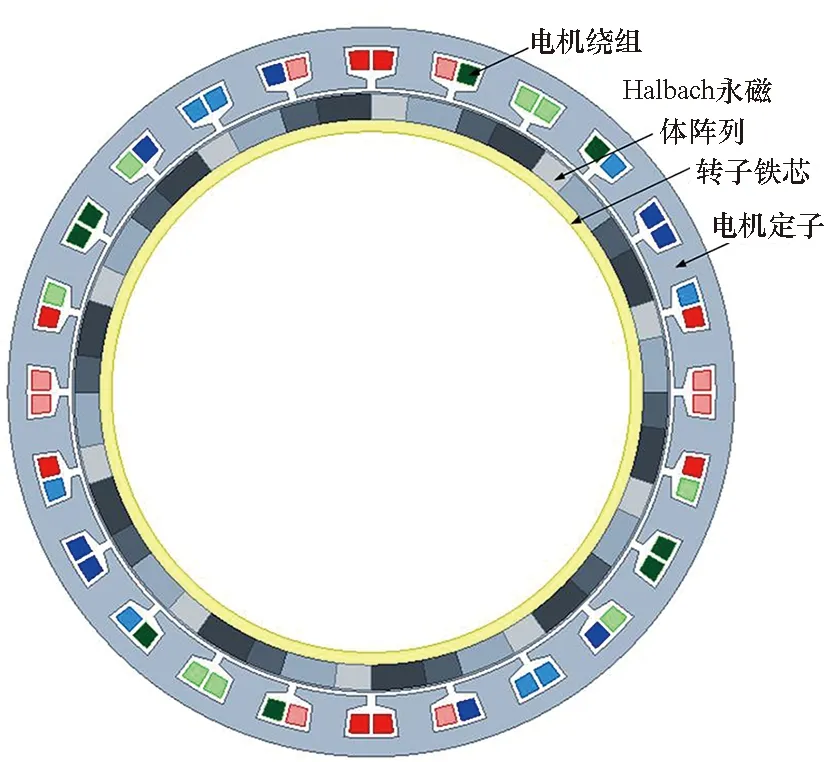
图1 Halbach永磁同步电机截面图Fig.1 Section of Halbach permanent magnet synchronous motor

经过有限元仿真,得到电机在额定状况运行时的空间气隙磁密如图2所示。

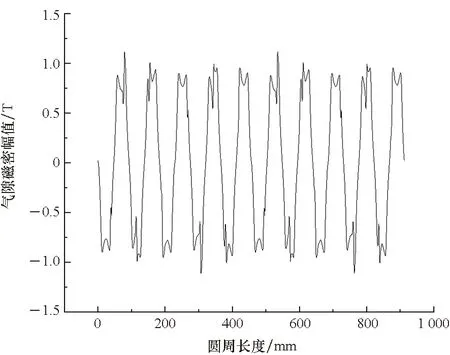
图2 电机的气隙磁密波形图Fig.2 Air gap magnetic density waveform of motor

在图2中,仅仅得到了电机的气隙磁密波形图,对于电机气隙磁密的函数表达式,可以通过正弦函数拟合算法来解决[10]。

周期信号在满足狄利克雷条件时,其电机空间气隙磁密波形可以认为是由各种谐波叠加而成,可表示成如下形式:

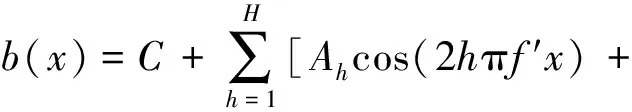
(6)

式中,x为圆周上的距离,H为最高谐波次数,C为直流分量,Ah和Bh分别为h次谐波的同相正交幅值,f′为信号的基波频率,n(t)是零均方差为e2的宽带噪声。 则h次谐波的相位和幅值分别为:

(7)

(8)

Ah和Bh可以通过遗传算法来估计其参数的初值,组成初始解向量。通过高斯-牛顿迭代法逼近加权最小二乘拟合方差,通过多次迭代,最终求得各次谐波的同相正交幅值[11]。

取最高谐波次数H为8,通过正弦函数拟合算法,可以得到空间气隙磁密函数表达式为:

b(x)=0.955 7sin(0.068 86x+3.07)+0.140 4sin(0.206 6x+3.046)+0.096 68sin(0.344 3x-0.183 9)+0.058 96sin(0.481 9x-0.156 4)+0.036 12sin(0.757 1x-2.925)+0.034 36sin(0.096 41x-1.657)+0.032 5sin(0.234 6x+0.75)+0.030 81sin(0.399 7x+0.597 8)

(9)

计算结果显示,输入与输出误差的平方和为2.87,多重测定系数为0.994,证明了正弦函数拟合效果良好[12]。

1.2 电磁力波分析

忽略切向磁密,电机的径向力密度表达式可由麦克斯韦定律求得,即:

(10)

其中:pn(θ,t)为径向电磁力密度;μ0为真空磁导率,大小为4π×10-7H/m。

不考虑时间变量,将式(5)代入式(10)中,就可以得到电机空间径向力密度的展开式。负载时,电磁力波的频率为2倍定子电流频率的整数倍[13-16]。其中,有两类径向力波引起的振动和噪声需要注意:

一类是2倍定子电流频率(333.3 Hz)下的力波。该频率下的振动噪声是由于气隙磁密中的基波磁场所产生的,该电机的基波空间极对数为10,所以力波的空间阶数为20阶,属于高阶力波,虽然该力波幅值较大,但是对电机振动和噪声的影响比较小。

另一类是主极磁场μ对极谐波和一阶齿谐波磁场(υ=p±Z1)所产生的低阶次力波,该低阶次力波是引起电机振动噪声的主要原因。该力波可以通过排出表1的形式来确定。

表1 力波表

由力波表分析可知,引起振动和噪声的力波主要有两个:其中一个由10对极的主极磁场和-14对极的齿谐波磁场相互作用所形成,另一个由30对极的主极磁场和34对极的齿谐波磁场相互作用所形成。两种力波的阶数均为-4阶,频率均为2倍的定子电流频率,即333.3 Hz。

2 3次谐波对电磁力的影响

在第1节中,已经得到了空间气隙磁密的函数表达式(9)和电磁力密度的表达式(10)。首先对圆周长度的自变量进行归一化处理,然后对空间电磁力密度函数进行快速傅里叶变换,得到电磁力密度幅值关于空间阶数的关系,如图3所示。

图3 电磁力密度的快速傅里叶变换Fig.3 Fast Fourier transform of electromagnetic force density

根据第1节的分析可知,引起电机振动噪声的主要力波阶次为-4阶力波,由图3可知该力波幅值为10 173.5 N/m2。影响该力波幅值的谐波磁场有4类:10对极的主极磁场、-14对极的齿谐波磁场、30对极的主极磁场、34对极的齿谐波磁场。其中,10对极的主极磁场在电机设计和优化过程中需保持不变,-14对极的齿谐波磁场和34对极的齿谐波磁场幅值较小且不易改变其幅值,对该力波幅值影响较小。

在电机设计和优化过程中,3次谐波磁场即30对极的磁场在气隙磁密中幅值较大,而且不同的电机设计使得该谐波的幅值差别也很大。基于此,有必要探究3次谐波对于-4阶电磁力密度幅值的具体影响。

将空间气隙磁密函数式(9)中的3次谐波的幅值设为自变量A3,并将其代入电磁力密度表达式(10),得到空间电磁力密度幅值关于A3与x的函数关系,其表达式如下:

(11)

对自变量x进行归一化处理,然后对式(11)进行快速傅里叶分解,得到电磁力密度幅值关于空间阶数的函数。取空间阶数为4阶,即可得到-4阶力密度幅值关于3次谐波幅值A3的函数关系如下:

F(A3)=fFFT[pn(A3,x)]|(k=4)

(12)

-4阶力波幅值关于3次谐波幅值A3的函数图像,即式(12)所对应的函数图像如图4所示。

图4 力密度幅值关于3次谐波幅值的曲线Fig.4 The curve of force density amplitude with respect to the third harmonic amplitude

从图4中可以看出,随着3次谐波幅值的增加,电磁力密度幅值先减小后增大,并且存在最佳3次谐波幅值使得电磁力密度幅值最小。

另外,该函数曲线还证明了气隙磁密的正弦性与电机振动噪声的大小没有负相关的关系,有可能出现气隙正弦性很好而振动噪声性能很差的情况。

3 遗传算法求解最佳幅值

3.1 遗传算法原理

第2节中得到了-4阶力波幅值关于3次谐波幅值A3的函数关系,并且该函数存在一个A3,使得F(A3)为最小值。F(A3)函数十分复杂,使用一般的数学方法难以进行求解,但使用遗传算法可以很容易得到目标结果。

遗传算法是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法[17-18]。简单而言,遗传算法,即一个种群代表一组问题的解,使用群体搜索技术,不断对种群进行选择、交叉和变异等一系列遗传操作来使种群进化,最终新种群中将包含问题的最优解。

3.2 算法具体实现步骤

3.2.1 适应度函数

适应度即个体适应环境的能力,在遗传算法中用来评价个体的优劣,通常适应度高的个体更接近于问题的最优解。

适应度的目标函数不受连续可微分的条件约束,任意集合都可以作为其定义域。它作为遗传选择操作中的选择标准,直接影响了算法性能。

在本问题中,需要求解的是力密度幅值的最小值,因此在式(12)的基础上可构造适应度函数为:

ffit(A3)=-fFFT[pn(A3,x)]|(f=4)

(13)

3.2.2 选择算子

根据个体的适应度选择适应度高的个体,使其保留到下一代的操作称为选择操作。

基于各个个体被选择的概率与其适应度大小成正比的思想,Holland提出“轮盘赌法”[19]。该方法是一种基于比例的选择,若某个个体的自适应度为ffit(i),种群大小为Np,则该个体被选中的概率为:

(14)

3.2.3 交叉和变异算子

交叉操作首先要从交配池中随机确定一组需要交配的个体,然后根据其位串长度L,以特定的交叉概率Pc,随机选取一个或多个片段交换其染色体,使其组成一对新的个体。

变异操作是对种群中的每一个个体,以特定的变异概率Pm将一个或多个基因座上的基因值改变为其他等位基因值。本问题选取的基因为二进制基因,发生变异时,相应的基因值取反[20-21]。

3.2.4 参数确定

本问题所采取的适应度函数为式(13),遗传选择方法为“轮盘赌法”,初始化种群的数目Np=50,染色体的二进制编码长度即位串的长度L=20,交叉概率Pc=0.8,变异概率Pm=0.1,终止进化代数G=100。

4 计算结果及振动实测

4.1 遗传算法计算结果

图5为适应度进化曲线,从图中可以看出,随着迭代次数的增加,目标函数值逐渐收敛,最终计算结果为:当A3=0.776 1 T时F(A3)取得最小值。

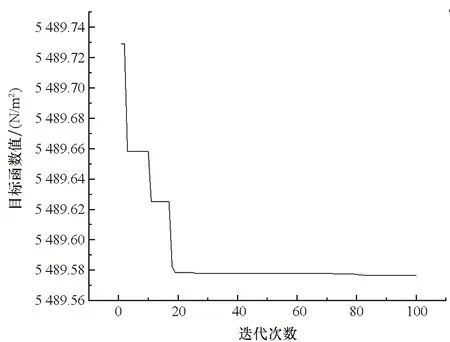
图5 适应度进化曲线Fig.5 Evolution curve of fitness

虽然A3=0.776 1 T时能够使得电机的振动噪声降低,但在进行电机设计时不仅要考虑振动噪声,还要注意其转矩脉动、电机铁耗以及永磁体的高效利用。一般电机的3次谐波不宜取得过大,在电机设计和优化中需要综合考虑。

4.2 电机振动仿真与实测

根据第2节和第3节的计算和分析,得到了Halbach结构电机气隙磁密3次谐波与-4阶力密度幅值的具体关系。现引入另一台电机,该电机除转子结构外,其余参数与本文分析的Halbach结构电机完全相同,其截面图如图6所示。

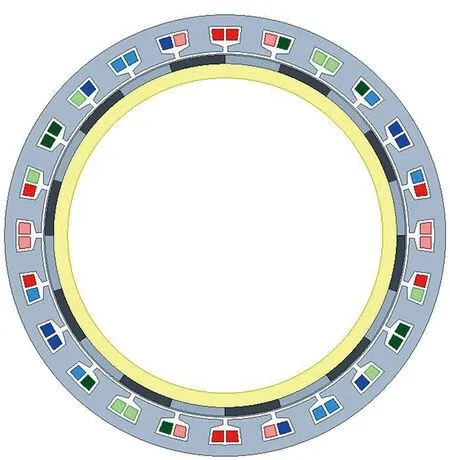
图6 径向充磁结构永磁同步电机截面图Fig.6 Cross section of permanent magnet synchronous motor for radial magnetizing structure

两台电机在额定功率时气隙磁密的傅里叶分解如图7所示。从图7中可以看出,两台电机气隙磁密的主要差别在3次谐波幅值上,Halbach结构电机的3次谐波幅值较小,气隙正弦度较高。

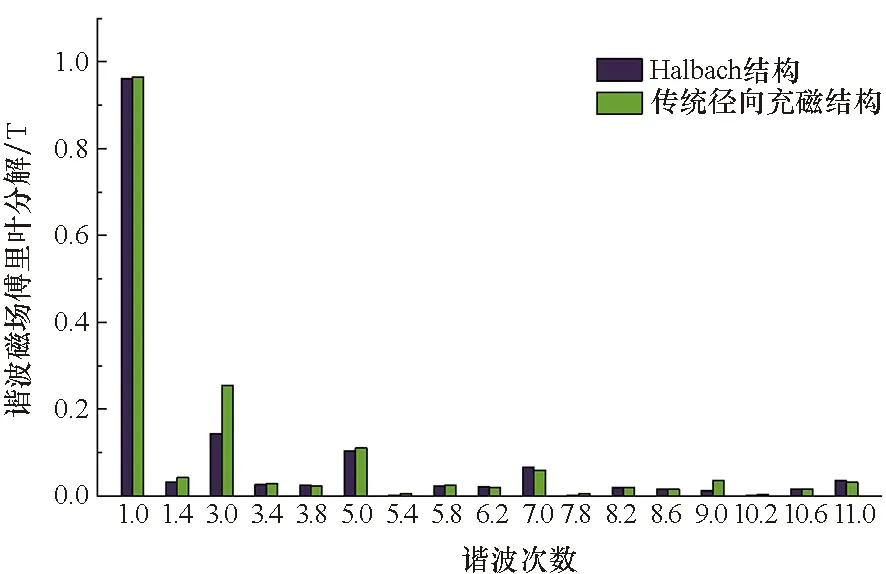
图7 两台电机在额定功率时的气隙磁密Fig.7 Air gap magnetic density of two motors at rated power

对两台电机进行电机振动的仿真,-4阶力波作用下的定子的总变形情况仿真结果如图8所示。从图8中可以看出,Halbach结构电机相比于径向充磁结构电机,其定子总变形量高出9.21%。从图9中可以看出,Halbach结构电机在333.3 Hz时的振动加速度响应也要高于径向充磁结构电机。Halbach结构电机的3次谐波含量小,气隙正弦度高,但振动噪声高于径向充磁结构电机。该实验结论与第2节所得出的结论一致,一定程度上验证了理论的正确性。

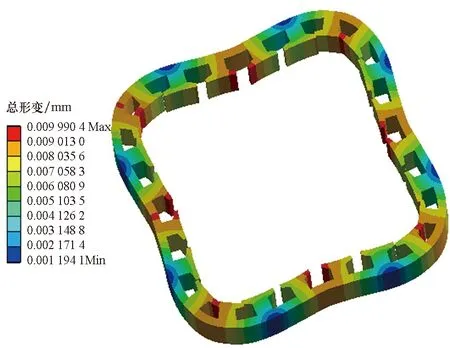
(a) Halbach结构(a) Halbach structure

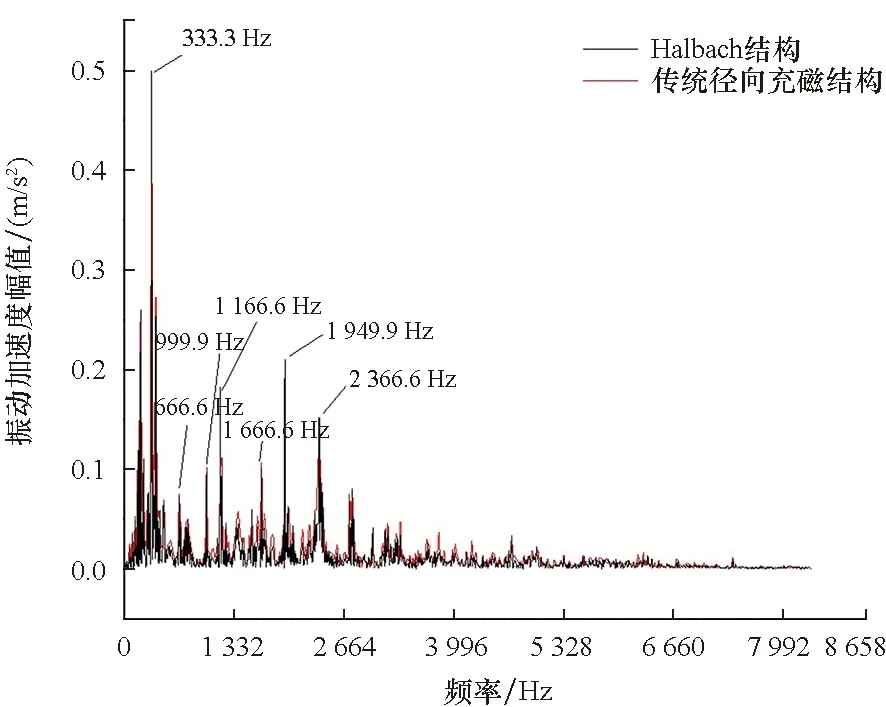
图9 两台电机振动实测Fig.9 Vibration measurement of two motors

对两台电机进行电机振动的实测,图9为两台电机振动实测对比的频谱图。

5 结论

本文以一台11 kW的Halbach结构的永磁电机为研究对象,建立了永磁同步电机气隙磁密和电磁力波的解析模型,在此基础上确定了引起电机振动噪声的主要力波分量。为了探究3次谐波与振动噪声的关系,建立了-4阶电磁力密度幅值关于3次谐波幅值的数学模型,得到了具体的函数图像,并通过遗传算法求解了最佳3次谐波幅值使得电机的振动噪声最小,实验与理论分析一致。基于此,得到如下结论:

1)电机的振动噪声并不取决于其气隙磁密的正弦性,进行低噪声电机的设计和优化时,应该从降低电磁力密度出发。

2)对于本文所研究的Halbach结构电机,随着3次气隙磁密谐波的增加,-4阶力波先减小后增大,3次气隙磁密为0.776 1 T时使得力密度幅值最小。

3)本文仅对电机的振动噪声求出了最佳3次谐波幅值,在进行电机设计时不仅要考虑振动噪声,还要注意其转矩脉动、电机铁耗以及永磁体的高效利用,图4所示的函数关系可为电机设计提供参考。

致谢

电机的振动信号测量工作是在海军工程大学蒋超和彭威博士的帮助下完成的,特此致谢!