潜艇上浮运动数值计算方法的研究与验证

魏可可,高霄鹏,马 骋,董祖舜

(1. 湖北工程学院 机械工程学院, 湖北 孝感 432000; 2. 海军工程大学 舰船与海洋学院, 湖北 武汉 430033; 3. 海军研究院, 北京 100161)

作为现代国防力量的重要组成部分,潜艇在出海远航及战略威慑中均发挥着重要的作用,然而潜艇应急上浮是一个极其危险的运动,潜艇从上浮到出水对潜艇稳性和艇中人员安全有着很大的影响[1],准确预报潜艇上浮运动是探索研究潜艇上浮运动控制规律以及潜艇安全上浮的前提。好多学者以SUBOFF标准模型为研究对象[2],对其上浮、操纵、直航等运动开展过研究[3];Carrica等[4-5]采用CFD Ship-Iowa V4对潜艇六自由度运动进行了的数值模拟,预报了不同工况下潜艇的操纵运动;基于真实桨和耦合虚拟桨的计算方法,Martin等[6]对潜艇的操纵运动进行了模拟,并对比分析了两种方法的计算结果;Chase等[7]基于雷诺平均纳维-斯托克斯(Reynolds average Navier-Stokes,RANS)方法,以SUBOFF为研究对象,网格划分采用重叠网格,对潜艇的直航和自航运动开展了仿真模拟;周广礼等[8-10]基于RANS方法,采用动网格,模拟了SUBOFF潜艇的上浮-出水运动,并监测了潜艇姿态变化;孙斌等[11]和孙济政等[12]对潜艇大型集体逃生舱做了上浮优化方案,基于CFD对逃生舱的上浮开展了仿真模拟,对逃生舱的上浮速度进行了分析;钱恒等[13]依据客观事实和相关实例,构建潜艇极地破冰上浮自然环境风险综合评估指标体系,并提出基于云变换-三角模糊数随机模拟的模糊层次分析法风险评估模型;吕帮俊等[14]基于潜艇操纵运动仿真数学模型,对高压气吹除主压载水舱后潜艇应急上浮过程的运动状态进行了预报;闫朋[15]基于CFD软件STARCCM+提出了一套有效的数值计算方法,通过对模型试验结果与数值计算结果的分析,总结了初始航速、稳心高、浮力载荷作用位置和艉舵角对潜艇应急上浮运动的影响规律。

以上对潜艇上浮运动的研究主要局限于数值计算,对其相关试验研究和数值方法的验证较少。本文以全附体的SUBOFF(指挥台含有舵)为研究对象,对其上浮运动的数值计算方法开展了研究,并与模型上浮试验进行了对比验证,证明了数值计算方法的可行性。

1 研究对象

SUBOFF是由美国泰勒研究所提供的潜艇试验模型,因为该模型是标准模型,所以进行过许多试验,在原SUBOFF模型基础上,在其指挥台围壳上增加了舵,修改的SUBOFF模型如图1所示,表1则给出了模型相关参数。

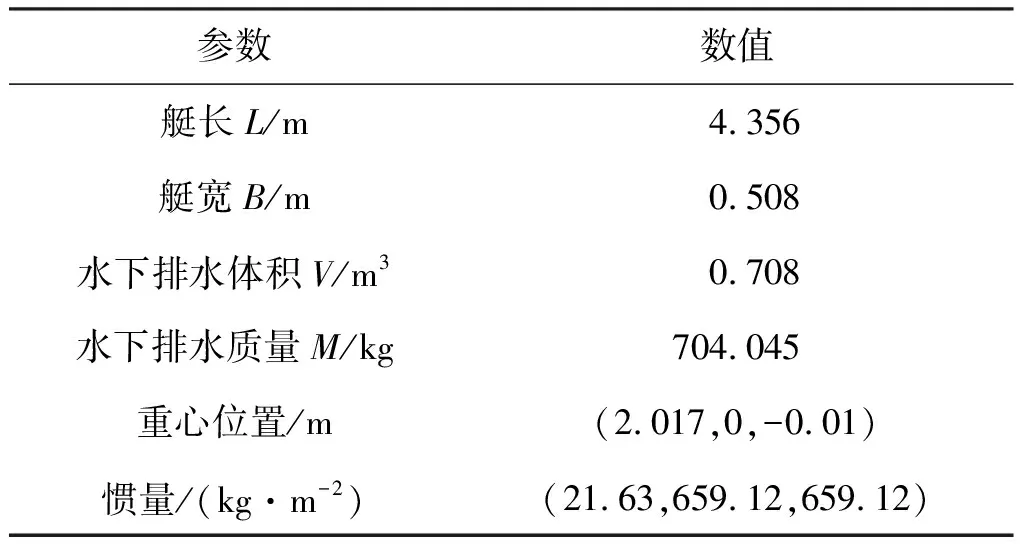
表1 模型主参数

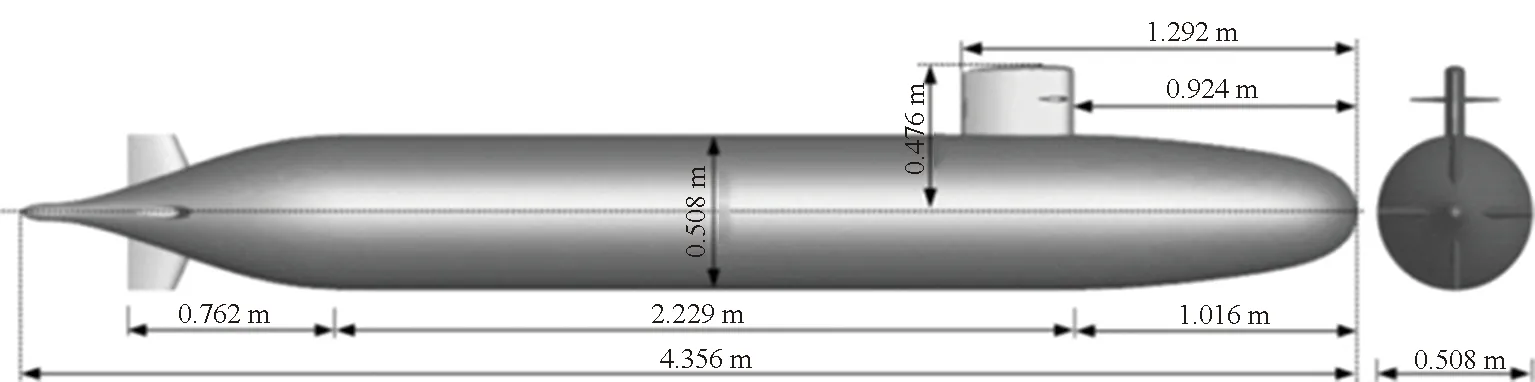
图1 艇体三维模型Fig.1 Three dimensional model of hull

2 数值计算方法

2.1 坐标系

为了便于对潜艇上浮运动的分析和对相关结果参数的监测,根据国际水池会议(ITTC)发布的权威标准,采用E-ξηζ为大地坐标系,原点E可选地球上某一定点,如海中的任一点;G-xyz为随艇坐标系,随艇坐标系的原点位于艇的重心G处。潜艇的上浮的运动可分解为水平面运动和垂直面运动,因此其坐标系也可分为两种,如图2所示。

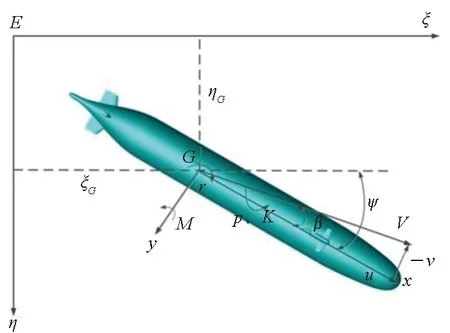
(a) 水平面运动坐标系(a) Coordinate system of horizontal motion

漂角β为航速V与x轴之间的夹角;α为来流的攻角;V在随艇坐标系上的投影为(u,v,w);潜艇的角速度Ω在随艇坐标系上的投影为(p,q,r);潜艇所受的外力F在随艇坐标系上的投影为(Fx,Fy,Fz);潜艇所受的力矩Q可用随艇坐标系上(K,M,N)来表示;潜艇的位置坐标可用随艇坐标系原点的地面坐标值(ξG,ηG,ζG)来表示;潜艇的姿态角可用相对于大地坐标系的三个姿态角(φ,θ,ψ)来表示,其中φ为横倾角、θ为纵倾角、ψ为航向角。

2.2 控制方程

潜艇的上浮到出水运动是复杂气液耦合黏性流体运动,对其开展数值模拟时,主要以连续性方程和动量方程为基础,方程的形式为:

(1)

其中,ρ为流体密度,xi、xj为i、j方向的坐标,ui、uj为流体速度沿i、j方向的分量,p为静压,fi为单位质量力。

2.3 重叠网格及其划分

对于潜艇上浮运动的模拟,基于重叠网格技术,计算域主要由背景域和重叠网格域组成,重叠网格域位于背景域里面,重叠网格域是跟随潜艇一起运动的,为避免重叠网格域随艇体运动移出背景域所设定的加密区,需将艇体在平面内的运动投影至背景域,即通过自编程序将潜艇在大地坐标系下的水平移动速度和垂直移动速度赋予背景域,背景域随艇体移动。不同时刻潜艇上浮运动重叠网格应用情况如图3所示,潜艇运动过程中,在水平面内重叠网格域与背景域不发生相对移动,仅存在相对转动;而在垂直面内,重叠网格域相对整体域可垂向移动、首摇、纵摇及横摇。

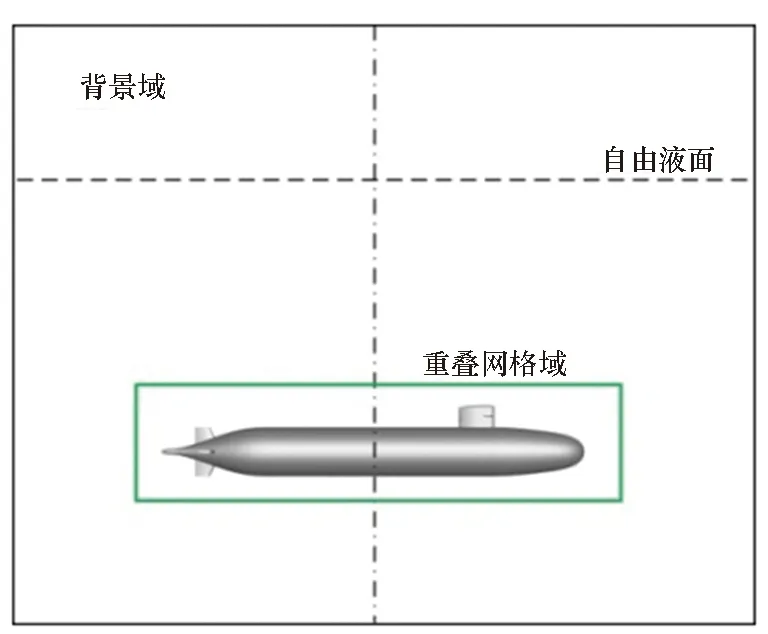
(a) 初始时刻(a) Initial moment

(b) 水面时刻(b) Moment of water surface

计算域采用方形域,尺寸大小为9L×4L×4.8L,潜艇上浮运动的计算域和艇体的网格划分如图4所示。

图4 SUBOFF模型上浮运动的计算域及艇体的网格Fig.4 Grid of computational domain and hull of SUBOFF model buoyancy motion

2.4 湍流模型的选取

为了更好地模拟潜艇上浮运动,需要湍流边界层,而湍流模型以k-ω模型为基准,采用黏流方法开展潜艇上浮运动数值模拟时,不同的湍流模型对计算的精度是不同的,众多学者已针对该问题开展了大量研究,但所得的结论存在较大差异。本文主要研究Standardk-ω和 剪切应力输运(shear stress transport,SST)(Menter)k-ω湍流模型对潜艇上浮运动参数结果的影响,对其开展优化分析。

Standardk-ω湍流模型方程为:

(2)

SST(Menter)k-ω湍流模型方程为:

(3)

其中,V为体积,μ为动力黏度,σk和σω为模型系数,fβ*为自由剪切修正因子,fβ为涡流延伸修正因子,Sk和Sω为源项,k表示湍动能,ω为特殊湍动能耗散,其余参数具体形式及参数值参见文献[16]。

潜艇的上浮运动和水面直航运动都涉及湍流边界层的运动,由于水面直航更加易于对潜艇拖曳阻力的测量,且湍流模式对潜艇水动力性能及运动形式并无影响,因此基于拖曳阻力试验,对Standardk-ω湍流模型和SST(Menter)k-ω湍流模型进行优选,为后续潜艇上浮运动的数值研究奠定基础。为此,分别以SUBOFF全附体模型和裸艇体模型为研究对象,对其展开静水中阻力的数值计算,并与试验值进行对比,模型的三维图如图5所示,对比结果如图6所示。

(a) 全附体模型(a) Model of full appendage

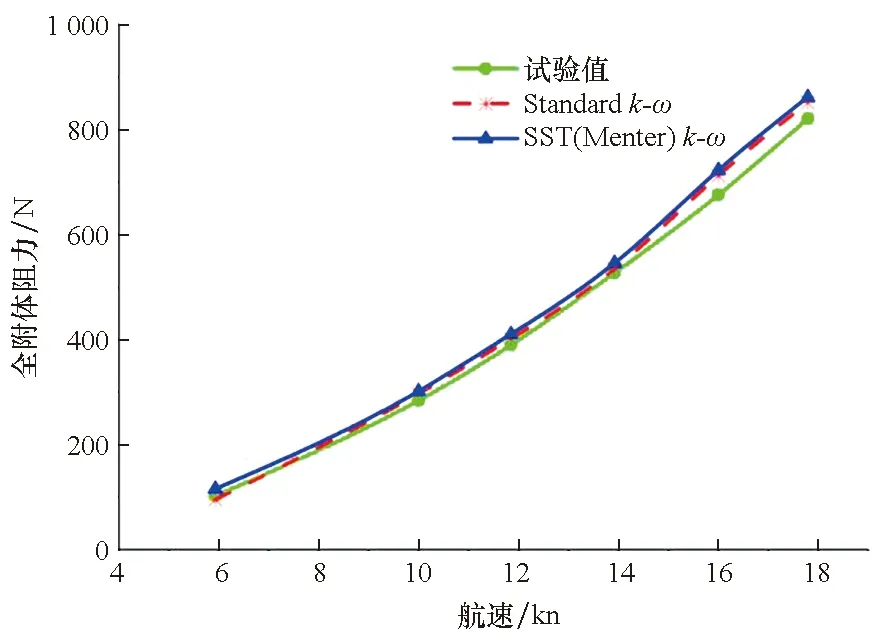
(a) 全附体模型结果(a) Results of the full appendage model

图6给出了SUBOFF全附体模型和裸艇体模型在航速分别为5.93 kn、10.00 kn、11.85 kn、13.92 kn、16.00 kn、17.79 kn时Standardk-ω湍流模型和SST(Menter)k-ω湍流模型下的拖曳阻力数值计算结果,同时与试验值进行了对比。从图6中可知,无论是全附体模型还是裸艇体模型,在低航速阶段,两种湍流模型的数值计算结果与试验结果基本一致,但在中高速阶段,Standardk-ω湍流模型的数值计算结果精度更高。由此可知,Standardk-ω模型可作为优选的湍流模型。

2.5 离散格式的选取

在网格上对离散的值建立差分方程的方法称为差分格式,差分方程的本质就是连续空间上的微分方程。当界面的物理量需要考虑方向时,对网格的离散可采用迎风格式,潜艇的上浮运动是一个多维多方向的运动,因此在数值模拟中采用迎风格式对网格进行离散。

以全附体的SUBOFF为研究对象,对其开展了一阶和二阶迎风格式的上浮运动数值计算,分别计算了全附体的SUBOFF模型上浮运动到出水过程中的纵向力、横向力、垂向力、纵向力矩、横向力矩以及垂向力矩,如图7所示。从图中可知,两种迎风格式下潜艇上浮运动的力和力矩的计算结果差别较小,即两者的计算精度相当,但考虑实际的计算时间,二阶迎风格式要优于一阶迎风格式,同时,基于一阶迎风格式,二阶迎风格式包含了物理量在节点间的分布曲线,因此也考虑了曲线曲率变化的影响。综上,潜艇上浮运动的数值计算优选二阶迎风格式。

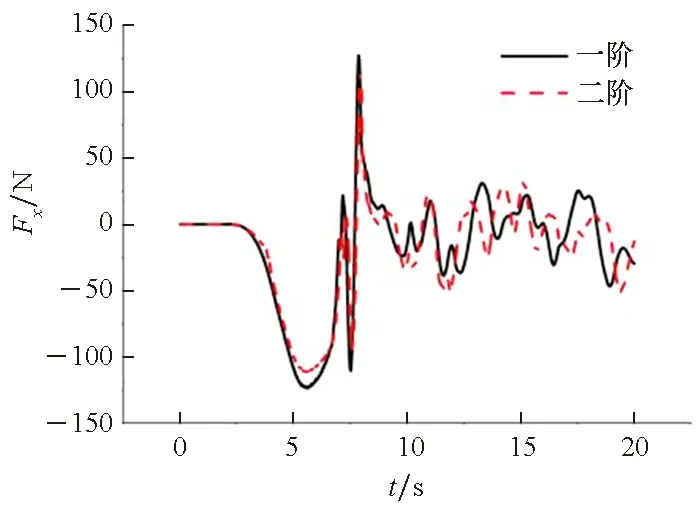
(a) 纵向力(a) Longitudinal force

3 模型上浮试验

3.1 上浮试验平台

为了验证数值计算方法,须开展潜艇的模型上浮试验。模型上浮试验主要依靠上浮试验平台来进行,潜艇的上浮是从水下到水面的六自由度运动,因此该试验平台必须含有能固定模型及释放模型的装置。同时为了保证在试验前,潜艇能下潜到指定的水深,因此该试验装置应含有可以承载潜艇模型的平台并能调节不同的潜深。该试验平台包含的基本装置有:平台底盘(内置水密发动机)、支撑架、拖车平台及模型、升降支座、释放器、轨道、升降装置、水下高清摄像机等设备,试验平台主要构件的尺寸如表2所示。

表2 平台主要结构装置的尺度及质量

3.2 试验系统及试验仪器的简介

整个潜艇模型上浮系统主要由岸机系统和上浮试验平台组成,其中,岸机系统主要由监测系统和控制系统组成,监测系统通过零浮力光纤和数据线分别和艇体以及高清水下摄像机相连,负责实时监测艇的倾角、加速度、水深等参数的时历变化以及实时记录艇体水下运动姿态;潜艇模型上浮试验系统如图8所示。

图 8 潜艇模型上浮系统示意图Fig.8 Schematic diagram of submarine model uplift system

为了精确完成潜艇应急上浮模型试验,试验时采用机载式数据采集记录系统进行数据的采集与记录,采用姿态仪对潜艇的横倾、纵倾及艏摇等姿态角进行测量,采用深度传感器对潜艇模型的水深进行实时测量,并在艇体的艏、舯、艉三个位置安装了三轴加速度传感器。

机载式数据采集记录系统、姿态仪及加速度传感器置于模型内部密封舱体内部,深度传感器固定在模型密封舱盖外端面,艇体上浮试验仪器设备的具体布置位置及功能如下:

1)姿态仪固定于重心处,可以实时测量艇体上浮过程中的姿态角;加速度传感器3个,均为3轴加速度传感器,分别固定于艇体轴线上艏、舯、艉三个不同纵向位置处,以测量艇体上浮到出水全过程中的运动状态。

2)水深传感器固定在模型密封舱盖外端面与水接触,可以实时测量模型上浮过程中的潜深位置;机载式数据采集记录系统置于艇体内部,可以直接采集姿态仪、加速度、深度传感器的测量数据。

3)岸上布置的上位机主要采集数据和实时监测艇体的姿态角、加速度、水深等参数的时历结果。

4)水下摄像机主要拍摄艇在不同工况下艇体上浮到出水的运动轨迹和运动姿态,并实时传回岸机。

3.3 试验步骤

在开展模型上浮试验前,根据需开展的试验工况对模型状态进行调试,模型调试好在水下拖车平台上进行安装和固定,在岸机上对整个测试系统的可靠性进行检查,确保系统在运行时无误;对模型的舱盖进行密封,对模型进行气密性的检查;对上浮试验平台通电,将模型下潜至所需的水深位置,启动水下拖车平台,释放模型上浮;在上浮试验过程中,实时对模型数据进行采集并对模型的轨迹及姿态录像;完成上浮试验后,对模型进行打捞回收,更换模型状态,进行下一个工况的模型试验准备。

4 不确定性分析

根据不确定度的相关计算方法[17],对潜艇上浮运动的计算结果开展不确定性分析,研究所构建的数值计算方法是否可行。验证和确认是开展不确定性分析的重要的两个流程:验证就是对数值误差的不确定度USN开展研究,迭代次数、网格划分、时间步长等因素都会导致数值误差的发生;确认就是对数值的不确定度USN开展研究,主要对误差E和确认不确定度UV来开展对比分析[18-20]。

4.1 验证

对于潜艇上浮数值模拟进行验证,主要是针对网格收敛性和时间步长收敛性开展的。本文主要对不同正上浮力下潜艇零速自由上浮的数值计算结果进行网格收敛性和时间步长收敛性开展研究。

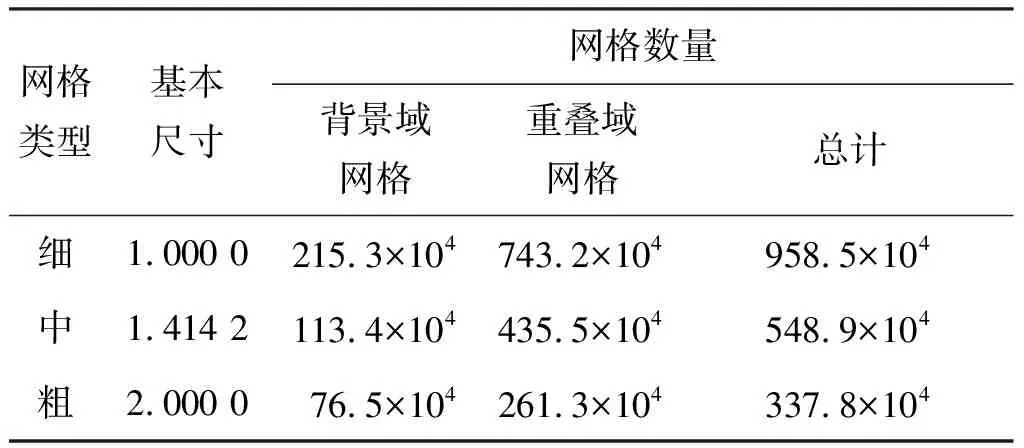
表3 不同网格类型

以不同正上浮力占比下的垂向速度为考量对象,表4和表5分别给出了网格收敛性结果和时间步长收敛性结果。

表4 网格收敛性验证结果

表5 时间步长收敛性验证结果

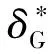
(4)

其中:ε32为粗、中网格数值结果之差,ε32=S3G-S2G;ε21为中、细网格数值结果之差,ε21=S2G-S1G;Pkest为数值计算中首项准确度极限阶数的估算值,参考文献[19]取2。

4.2 确认

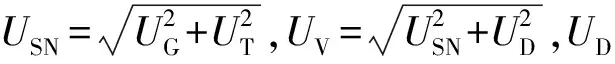
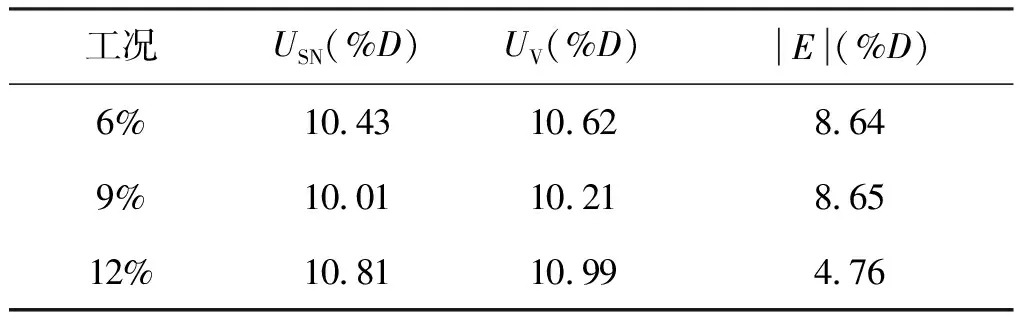
表6 数值计算的确认结果

由表6可知,数值计算结果与试验值的对比误差|E|均小于确认不确定度UV,这说明三种工况下数值计算的结果都得到了确认,由此说明该数值计算方法可行和可靠。

5 数值计算的验证

5.1 上浮运动数值计算流程

对于潜艇的上浮运动问题,采用重叠网格,在一个时间步长内,依据所需的工况,输入初始条件和边界条件,初始化流场后可运行计算,基于控制方程求解艇体表面的速度场和压力场,进而可求出艇体表面所受的力和力矩,将所求得的力和力矩带入潜艇6DOF运动方程中就可求取所需艇体上浮运动参数。潜艇在静水中上浮运动的数值计算方法如图9所示。

图9 数值计算的流程图Fig.9 Flowchart of numerical calculation

5.2 数值计算结果与试验结果的对比

试验工况为:潜艇质量为640.48 kg,正上浮力为621.56 N,潜深3.5 m,静水,航速为零。在此工况下开展潜艇上浮运动的数值计算。在进行数值模拟时,选取分离式(segregated flow)求解控制方程,对于压力和速度的修正选取压力耦合方程的半隐式算法(semi-implicit-method for pressure linked equations,SIMPLE),网格离散格式选用二阶迎风格式。涉及非稳态计算时,设置数值计算过程中的时间步长Δt=5×10-3s。对于湍流模型,选取Standardk-ω。试验场地选择室外波浪水池。全附体SUBOFF模型上浮试验如图10所示,数值计算结果与试验结果的对比如图11所示。

图10 SUBOFF模型上浮试验Fig.10 Floating test of SUBOFF model

(a) 纵向速度(a) Longitudinal speed

从图11中可知,数值计算结果与上浮试验结果的变化规律大致相同,数值计算结果与试验结果具有较好的吻合度;数值计算的纵向速度和垂向速度与试验结果相比很接近,纵倾角和横倾角的数值计算结果与试验结果存在有一定的误差,但误差较小。由此可知,该数值计算具有较好的可信度,从而验证了该数值计算方法可以适用于潜艇上浮运动的研究。

6 结论

本文介绍潜艇上浮运动的数值计算方法,并对数值计算中湍流模型、离散格式等进行了优选,介绍了潜艇的模型上浮试验,对数值计算的不确定度进行了分析,且与上浮模型试验的结果进行了对比,主要得到以下结论:

1)通过分别对不同湍流模型以及不同离散格式的对比分析,优选了Standardk-ω的湍流模型,选取了二阶迎风格式,由此确定了数值计算的基础;

2)基于网格收敛性和时间步长收敛性的分析,对数值计算的不确定度开展了研究,最终证明了数值模拟的可靠性;

3)针对潜艇六自由度上浮运动问题,采用重叠网格技术,并结合6-DOF刚体运动模型和DFBI模型,对潜艇上浮运动数值计算流程进行了阐述,同时对潜艇的模型上浮试验进行了介绍,该数值模拟方法和上浮试验可支撑潜艇上浮运动的相关研究;

4)基于模型上浮试验,数值计算结果与试验结果具有较好的吻合度,且误差较小,从而证明了该数值模拟方法的可行性和准确性。