非合作目标弹道系数解算研究及应用
刘舒莳,李勰,*,满海钧,陈光明,曹建峰,鞠冰
(1.北京航天飞行控制中心,北京 100094;2.航天飞行动力学技术重点实验室,北京 100094)
非合作目标泛指不能获得有效信息的空间目标,如来袭导弹、敌机、失效或故障航天器、空间碎片等。自1957 年第一颗人造卫星上天以来,已有近24 000 个目标陨落坠入地球大气层,其中大部分是非合作目标。再入过程中,虽然大多数航天器在与大气相互作用过程中烧蚀、熔融和解体,但仍有10%~40%的器件落到地面,对人类安全和财产带来潜在威胁[1-3]。随着中国航天事业的不断发展,服役期满航天器再入大气的频率越来越高,对这些目标开展陨落预报,体现了中国作为航天大国负责任的态度。另外,掌握他国在轨空间目标的运动特性,尤其是非合作目标,对于国土防空早期预警及增强空间态势感知能力,也具有十分重要的意义。
影响航天器再入陨落预报精度的主要因素包括轨道初始状态、弹道系数及大气密度。其中,弹道系数是计算大气阻力的重要参数,包含了航天器质量、外形和气动特性的组合参数,对于非合作目标,需要利用其轨道信息来解算弹道系数。
有学者利用卡尔曼滤波算法将航天器运动状态和弹道系数进行联合滤波估计,并对传统卡尔曼滤波进行了改进。例如,采用不敏卡尔曼滤波算法对非线性函数的概率分布进行近似[4-5],基于期望最大化迭代优化框架;文献[6]利用精密定轨过程中的残差信息,并结合空间环境变化对大气阻力系数修正。这些方法需要丰富的轨道观测数据,不适用于观测条件不理想的非合作目标。
美国空间监视网对大部分在轨目标进行监视、编目和维护,北美防空司令部将目标的轨道信息以双行根数(two line element,TLE)形式发布在Space-Track 网站。TLE 由于其完备性、实时性、精确性及开放性而备受关注,为非合作目标提供了有效的轨道信息[7-8],是解算非合作目标弹道系数的重要数据源。Gupta[9]和Shoemaker[10]等根据ti时刻TLE根数推算t时刻近地点hpi和 远地点高度hai,再根据t时刻TLE 根数计算t时刻近地点高度hpt和远地点高度hat,令 |hpi−hpt|和 |hai−hat|最小来获得最优弹道系数。据报道,该方法在航天器陨落的末期较准确,但是过于依赖TLE 中的偏心率,而偏心率的精度往往较低。为了弥补TLE 中偏心率精度较低的缺陷,Sharma 等[11]提出了一种同时估算弹道系数和初始偏心率的方法,使用响应曲面法拟合远地点高度来估计偏心率和弹道系数。由于TLE 中的半长轴精度优于偏心率,Sang 等[12]利用不同TLE 中半长轴的衰减估算弹道系数,Saunders 等[13-14]对其进行了改进,通过使用多天TLE,多次迭代提高弹道系数估算精度。但对于非合作目标,由于不知道其轨道机动情况,在使用多天数据解算时,如果发生轨道机动,则会降低弹道系数估算精度。
针对上述问题,本文在Saunders 方法的基础上进行了改进。首先,阐述了利用TLE 进行弹道系数估计的理论方法,分析了构造轨道半长轴衰减观测量的依据;然后,针对非合作目标特点,对TLE 中的半长轴做了平滑检测和二次判别,识别出野值、轨道机动和地磁暴3 种情况,比较了不同观测弧长对弹道系数解算的影响;最后,利用本文算法对天宫一号正常在轨和陨落期间解算的弹道系数进行了精度评估,并在天宫一号陨落预报中进行了验证。
1 数据与方法
1.1 基于TLE 的弹道系数估计
弹道系数B表达式[15-16]为
式中:m为航天器质量;CD为大气阻力系数;s为航天器迎风面积。
大气阻力对半长轴的影响主要体现为半长轴的长期衰减效应,即
式中:da/dt为半长轴的衰减率;v为航天器瞬时速度;µ为引力常数;r¨drag为阻力摄动加速度。
由TLE根数计算的半长轴记为atle,由式(3)计算:
式中:nk为TLE 根数中对卫星平均运动的描述量。
对于任意2 个连续时间间隔范围的半长轴衰减,可记为
将∆atle作为半长轴衰减观测量,构建条件方程。半长轴的衰减主要受大气阻力的影响,因此在给定时间间隔内,对式(2)进行积分,即可获取半长轴衰减的理论解算结果∆acomp,即
式中:ρ为大气密度。
积分区间即为2 个TLE 的时间间隔。对于式(6),可利用常规求积算法给出。需要说明的是,在积分求和过程中,给定了积分步长,则积分区间内每个步点上的 ρ、a和v,可利用数值积分计算。数值积分的初值包含初始历元时刻、初始位置速度和弹道系数,可通过SGP4 模型对TLE 进行单点转换得到。将半长轴的衰减展开,并略去高阶项,得到
式中:∆B为弹道系数改进量。
由于式(7)为超定方程,采用最小二乘迭代求解,设定相邻2 次迭代弹道系数改进量小于给定门限,方程收敛,从而得到最终的弹道系数。
计算流程如图1 所示。
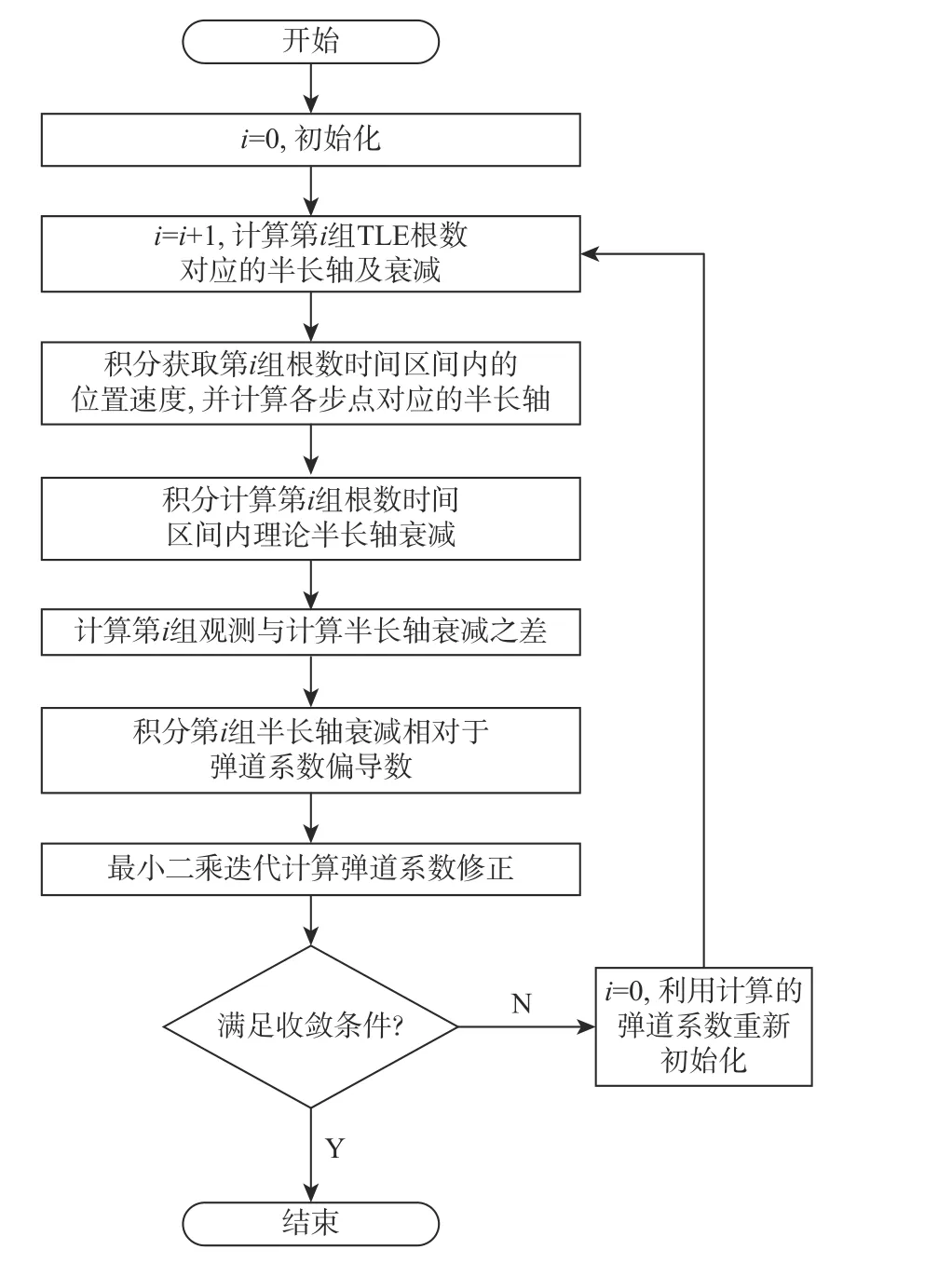
图1 弹道系数解算流程Fig.1 Flowchart of ballistic coefficient solution
1.2 轨道半长轴衰减分析
TLE 是用特定方法平滑掉了周期扰动项的平均轨道根数,对应的轨道模型是SGP4/SDP4 解析模型[17]。TLE 数据没有包含轨道精度信息,因此,利用天宫一号正常工作时段的精密星历对TLE 的预报星历进行了精度评估,从而确定构造半长轴衰减观测量的依据。
选取天宫一号2012 年1 月1 日至1 月10 日期间的TLE 预报星历和精密星历进行比对,由于大气阻力主要体现在高度变化率上,对TLE 轨道和精密轨道的高度变化率进行了比较分析。首先,去除瞬时精密轨道根数中的周期性变化(如地球重力场非球形的影响),得到每日的平根数;其次,根据TLE中的轨道倾角、偏心率和平运动周期计算半长轴;然后,利用样条插值将TLE 的半长轴插值到与精密轨道根数相同的历元;最后,依次计算精密轨道平根数半长轴和TLE 半长轴的每日衰减,并标示出两者高度变化率的偏差,图2 和图3 分别展示了两者每日和每2 日高度衰减情况。结果表明,TLE 高度变化率偏差的标准差为24.95 m/d 和30.6 m/(2d),轨道高度衰减平均为211 m/d 和422 m/(2d),TLE 反演出的每日轨道高度衰减误差为11.85%,每2 日轨道高度衰减误差为7.25%。由于常用大气模式精度约10%,利用TLE 的半长轴每2 日衰减量构造观测量,其精度能够较好地反映大气阻力的变化。
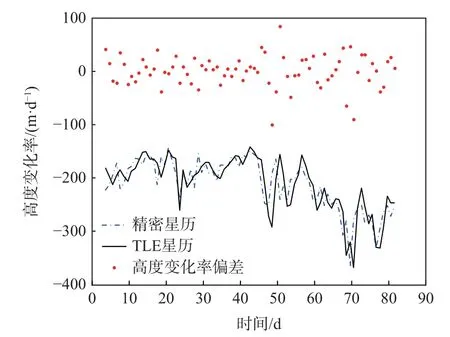
图2 TLE 星历与精密星历每日高度衰减对比Fig.2 Comparison of daily height attenuation between TLE and precision ephemeris
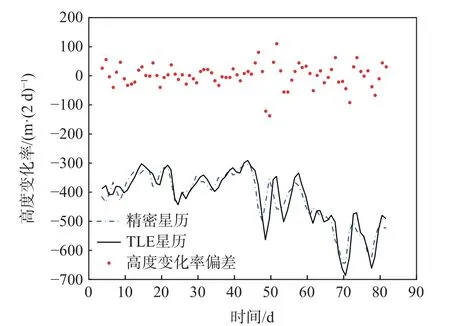
图3 TLE 星历与精密星历每2 日高度衰减对比Fig.3 Comparison of every two days height attenuation between TLE and precision ephemeris
1.3 TLE 数据预处理
由于飞行器在轨飞行过程中可能会发生轨道机动,造成半长轴变化,需要在预处理中检测轨道机动,对轨道机动前后的TLE 分别处理,即式(5)积分区间不能包含轨道机动。此外,为提高弹道系数计算精度,应剔除精度较低的TLE,在这个过程中需结合地磁指数变化进行识别,避免地磁暴引起的半长轴快速衰减被误判为低精度TLE。采用二次多项式拟合的方法对TLE 的半长轴进行初步检测和二次判别,具体方法如下:首先,利用SGP4 模型计算出所有TLE 的半长轴;其次,对连续的第1,2,3,5,6,7 个历元的半长轴进行二次多项式拟合,根据拟合的多项式计算第4 个历元的半长轴的拟合值a4p;然后,计算第4 个历元的拟合值与观测值的差异ε=a4p−a4t,并根据3 倍方差准则进行判别;最后,对于超过门限的 ε进行二次判别,结合地磁指数,识别出3 类情况,即野值、轨道机动和地磁暴。
对2012 年1 月至3 月的天宫一号TLE 半长轴进行初步平滑检测,门限值3 倍方差取20 m,如图4所示,发现有5 个时段(红框标识)的半长轴超过门限,图5 给出了同时期地磁指数ap(每3 h 均值),并用红框标出了超出门限的时段。可以看出,P1、P2、P3 和P4 时段都发生了地磁暴,导致P1、P2 和P4 时段航天器半长轴比平静期衰减得多,即a4t比拟合值a4p小,使得 ε超出门限,因此P1、P2 和P4 时段的TLE 不是野值,不应剔除;P3 时段虽然有微小地磁扰动,但a4t反 而大于拟合值a4p,可以认定P3 是野值;P5 时段平滑值与实测值差异达到100 m 以上,即使这个时段发生了地磁扰动,也应认定为发生了轨道机动。
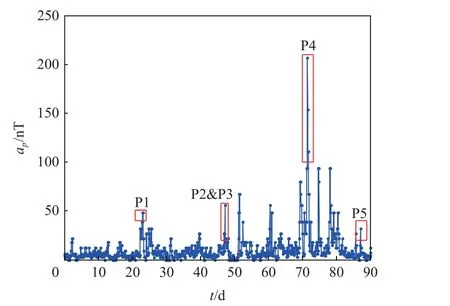
图5 地磁指数变化Fig.5 Variations of geomagnetic index
2 结果与分析
2.1 弹道系数精度比较与评估
为了评估TLE 解算弹道系数的精度,本节比较了不同方法解算弹道系数的差异。在精密定轨中,往往把大气阻力系数CD作为未知量与卫星的运动状态矢量一起解算,再利用式(1)求解弹道系数。定轨中尽可能采用高精度的动力学模型,包括JGM64×64 地球重力场模型、MSISE2000 大气密度模型,全面考虑了日月引力、太阳光压和地球固体潮汐等多种摄动力。选择天宫一号2011 年11 月19 日至2012 年12 月31 日期间的轨道资料进行比对,这段时期轨道资料丰富,飞行器性能稳定,地磁活动和太阳辐射处于中等活跃水平。利用每天的轨道观测数据进行轨道确定,并解算当日CD,结果如图6 所示,CD平均值为2.221 9,弹道系数平均值为0.009 4。同时,图6(b)给出了期间的太阳辐射指数F10.7 和地磁指数AP(日均值),可以看出,弹道系数与F10.7 有较强的相关性,尤其在27 d 周期变化方面有很强的一致性。飞行器质量是精确已知的,且随着发动机每次开机略有降低,飞行器姿态稳定的工况下每圈次的平均迎风面积也是稳定的,因此弹道系数的周期性变化是由CD变化引起的。大气阻力系数CD是描述大气粒子与卫星表面相互作用的无量纲系数,反映了粒子与卫星表面碰撞过程中的动量传递和能量耗散效率,其大小取决于卫星表面的材质、大气的成分和温度,以及入射大气粒子与卫星表面的夹角等因素[18-21]。在这些影响因素中,卫星表面材质在正常飞行过程中是稳定的,大气粒子与卫星表面的入射夹角平均值在每个圈次也是稳定的,因此可以推断,CD的周期性变化是由大气成分、温度的变化引起的,而大气成分、温度受太阳活动影响与F10.7 有很强的相关性。
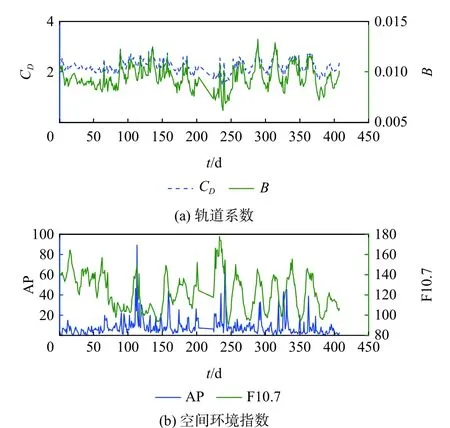
图6 精密定轨解算弹道系数和空间环境指数Fig.6 Ballistic coefficients solved by orbit determination and space environment index
图6 精密定轨解算的弹道系数展示了与F10.7的相关性,说明解算结果是准确可信的,但是在定轨过程中,弹道系数不可避免地吸收了大气模型、轨道测量数据和飞行器迎风面积等因素引入的误差,为此,需要对每日解算的弹道系数进行平滑处理。由于天宫一号弹道系数中的质量和迎风面积是精确已知的,从弹道系数中提取了物理意义更加明确的大气阻力系数。如图7 所示,分别采用3 d、5 d 和7 d 均值法对阻力系数平滑。可以看出,平滑处理后,不仅去除了随机误差,还保留了原来的周期性变化。因此,选取7 d 平滑处理后的阻力系数与TLE 解算的阻力系数比对。
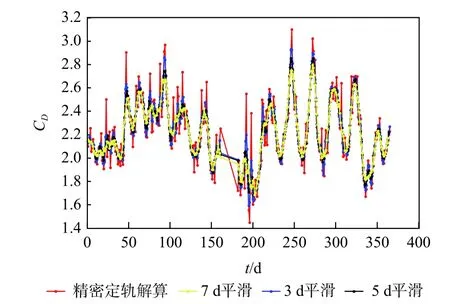
图7 精密定轨解算的大气阻力系数及其平滑值(起始日期2012-01-01)Fig.7 Drag coefficients solved by orbit determination and their smoothed values (start date Jan.1, 2012)
利用TLE 解算天宫一号2012 年全年的大气阻力系数CD和弹道系数,解算过程中采用了不同时间间隔的TLE 构建观测量 ∆atle,即式(6)中的积分区间,分别设置为2 d 和3 d;观测弧段分别选取7 d和10 d,即分别采用7 d 和10 d 的TLE 解算一个弹道系数。4 组解算结果如图8 所示,同时给出了精密定轨的解算结果。可以看出,TLE 解算的4 组结果与精密定轨解算结果的变化趋势十分吻合,都能反映出太阳活动的周期性变化;不同时间间隔的观测量对解算结果影响不大;观测弧段为10 d 的解算结果更稳定,曲线更加平滑。
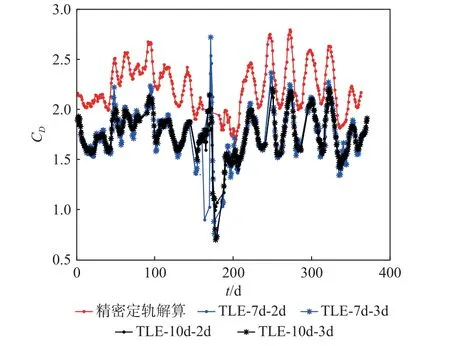
图8 TLE 解算的大气阻力系数(起始日期2012-01-01)Fig.8 Drag coefficients solved by TLE (start date Jan.1, 2012)
2.2 天宫一号陨落分析
2.2.1 陨落阶段弹道系数解算分析
天宫一号是中国第一个非受控再入大气层的超大型航天器,于2016 年3 月16 日正式终止数据服务。在大气阻力下影响下,天宫一号轨道不断衰减,最终于2018 年4 月2 日8 时15 分落入南太平洋。天宫一号最后30 d 平均轨道高度如图9 所示。陨落之前数月难以得到精确的姿态信息,从而难以估算式(1)中的迎风面积,因此适宜采用1.1 节的方法,对包含了CD和迎风面积的弹道系数联合估算。
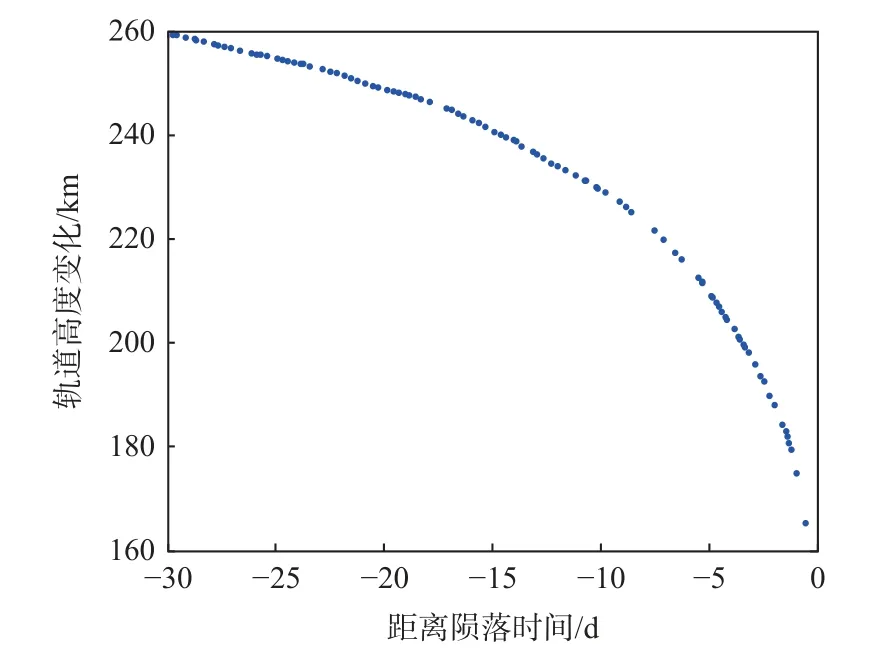
图9 天宫一号陨落前轨道高度变化Fig.9 Height variation of Tiangong-1 before reentry
使用1.2 节的方法对陨落前40 d 的TLE 的半长轴进行平滑检测,结果如图10 所示。陨落前40 d至陨落前23 d,平滑值与TLE 半长轴差异20 m 之内,说明这期间飞行器高度衰减变化稳定,TLE 精度较高。陨落前22 d 至陨落,平滑值与TLE 半长轴差异逐渐增大,陨落前2 d 的差值甚至超过200 m,初步判断可能是以下原因造成的:①陨落前15 d 至陨落前14 d 有地磁扰动;②飞行器姿态不稳定导致迎风面积变化;③200 km 以下大气密度更加复杂多变;④TLE 本身的精度较差。前3 个原因造成的差异不影响弹道系数解算,不需要剔除,只需剔除精度较差的TLE。经过二次判别,陨落前3 d 至陨落的数据大部分不可用,因此后续轨道预报中陨落前2 d 和陨落前1 d 的弹道系数使用陨落前3 d 的结果。
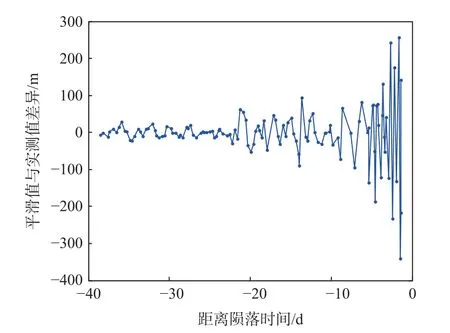
图10 天宫一号TLE 半长轴平滑检测结果Fig.10 Semi-major axis smoothing test results for Tiangong-1 TLE
基于2 d 间隔的TLE 构建观测量 ∆atle,分别采用每5 d、7 d 和10 d 的观测弧段解算一个弹道系数,结果如图11 所示。弹道系数随着观测弧段的增长,弹道系数的变化趋势趋于平缓。文献[22]利用Sentman 模型计算了150~300 km 高度范围不同构型卫星的大气阻力系数,认为圆柱体卫星(与天宫一号构型较接近)的阻力系数在2.3~2.7 之间变化,最大值是最小值的1.17 倍。图11 给出的类似高 度 范 围 的 弹 道 系 数(TLE-10d-2d)在4.7×10−3~5.4×10−3之间变化,最大值是最小值的1.15 倍,变化幅度与Sentman 模型计算结果接近。
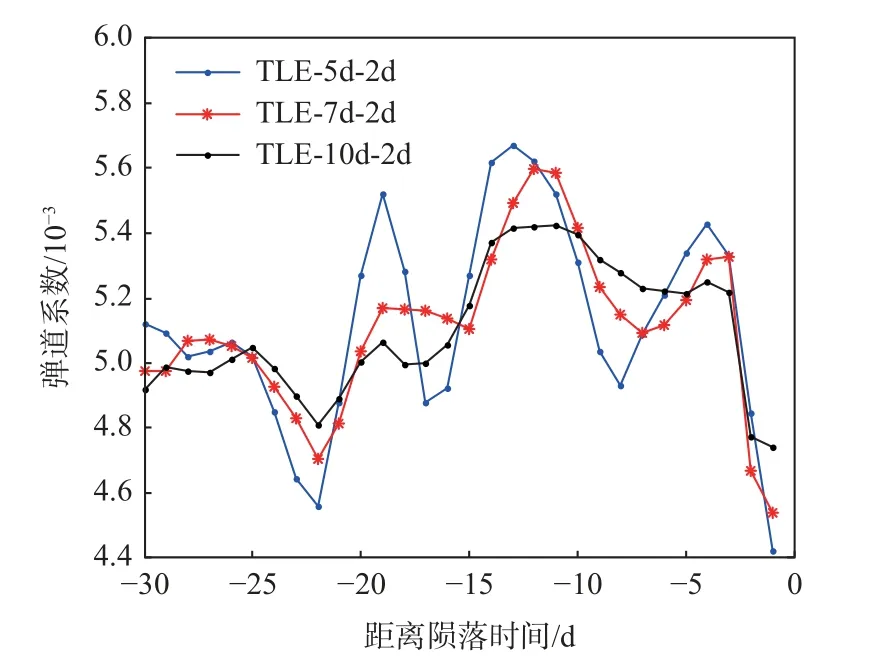
图11 陨落前30 d 不同观测弧段解算的弹道系数Fig.11 Ballistic coefficients solved with different observation arcs before 30 days of reentry
2.2.2 天宫一号陨落时间预报
从2018 年3 月3 日起,使用2 种方法基于美国空间监视网每日发布的天宫一号TLE 对陨落时间进行预报。第1 种方法:利用SGP4 模型计算TLE历元时刻的卫星位置速度 (r,r˙),以此作为初始轨道,利用自主定轨软件做轨道预报,计算卫星高度降至125 km 的时刻Tr,预报过程中使用64×64 阶重力场模型和MSISE00 大气密度模型,空间环境参数太阳流量F10.7 和地磁指数AP 使用陨落前30 d 的均值,弹道系数使用图11 中TLE-5d-2d 解算值;第2 种方法:利用SGP4 模型和TLE 进行轨道预报,计算卫星高度降至125 km 的时刻Tr′。用上述2 种方法逐日预报天宫一号陨落时间,如图12 所示。可以看出,利用第1 种方法解算的弹道系数预报天宫一号陨落,最大误差15 d,平均误差7.03 d,精度显著优于第2 种方法(最大误差25 d,平均误差15.6 d)。
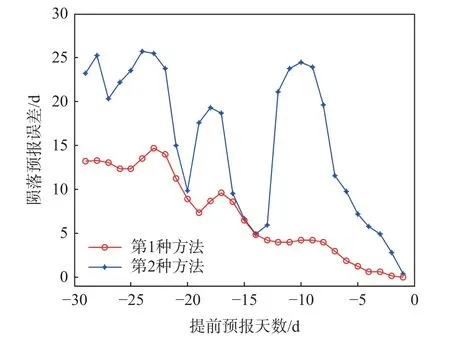
图12 使用不同弹道系数的预报误差Fig.12 Prediction errors using different ballistic coefficients
天宫一号陨落事件在国际上备受关注,世界主要航天大国都发布了各自预报的再入窗口,如图13所示。统计了俄罗斯国家航天集团、美国国家航空航天局、欧洲航天局、日本宇宙航空研究开发机构和印度空间研究组织−4 d~−1 d 发布的再入窗口,其中缺少美国国家航空航天局(−3 d)、欧洲航天局(−2 d)、俄罗斯国家航天集团(−1 d)和日本宇宙航空研究开发机构(−1 d)的数据。需要说明的是,在轨道预报中使用的太阳辐射指数F10.7 和地磁指数AP 是陨落前30 d 的实测平均值,因此可直接计算出航天器再入大气层(125 km)的时刻,而各国是基于F10.7 和AP 的一个变化范围做出的轨道预报,因此发布的再入窗口也是一个时间范围,为方便比较,取各国发布的时间窗口的中间值。从图13 的统计结果可看出,本文第−4 d、−1 d 的预报精度最高,第−3 d、−2 d 的预报精度处于中间水平,总的来看,本文的陨落预报精度在各航天大国中处于领先水平,说明弹道系数解算方法是正确可行的。
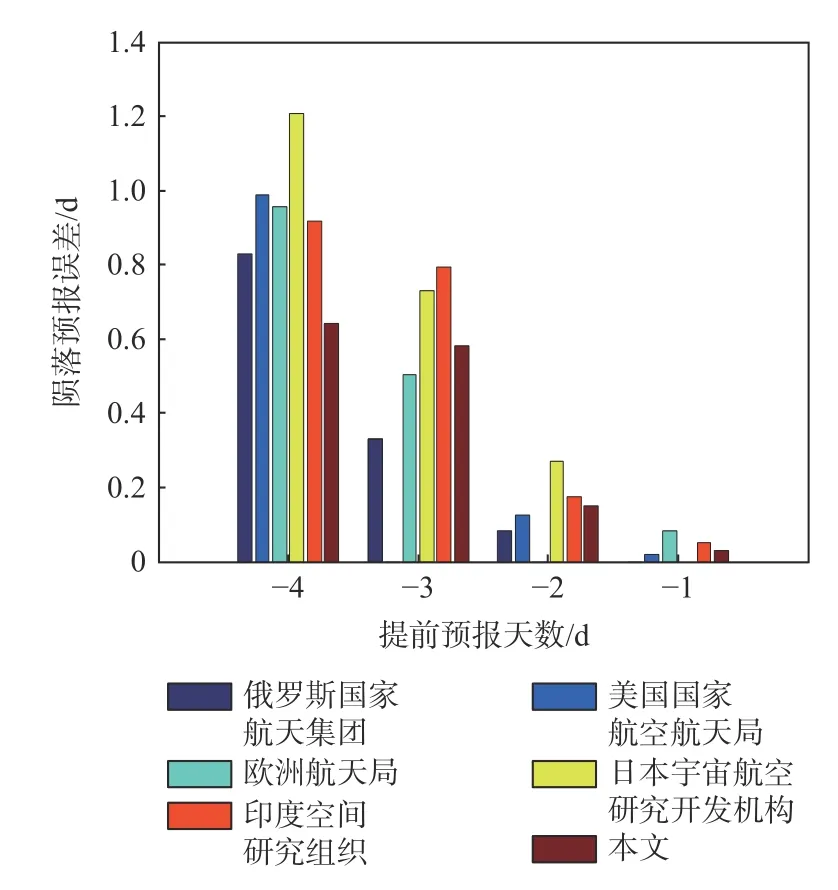
图13 各国与本文发布的天宫一号陨落预报误差比较Fig.13 Comparison of Tiangong-1 reentry forecast errors issued by various countries and this paper
3 结 论
本文研究了利用TLE 的半长轴衰减反演非合作目标弹道系数的方法,总结如下:
1)对TLE 的半长轴精度进行了评估,验证了半长轴衰减信息用于反演弹道系数的可行性,确定了使用2 d 间隔的TLE 半长轴构造轨道衰减观测量。
2)研究了TLE 预处理方法,通过多项式平滑检测和二次判别识别出野值、轨道机动和地磁暴3 种情况。
3)利用天宫一号2012 年TLE 解算了全年的弹道系数,并与精密定轨解算的弹道系数进行了比对,两者变化趋势十分吻合,且都能反映出太阳活动的周期性变化。
4)解算了天宫一号陨落前30 d 的每日弹道系数,并利用解算结果进行了陨落预报,与世界其他国家发布的预报比较,解算的弹道系数能够获得优于其他国家的预报精度。
5)利用TLE 的半长轴衰减信息解算非合作目标弹道系数在航天工程中是切实可行的方法,对于非合作目标的监视,碰撞预警和规避提供了更精准的目标特性信息,对提升中国空间安全和态势感知能力具有重要意义。
本文提出的弹道系数解算算法仅适用轨道高度600 km 以下的目标,对于轨道高度400~600 km的航天器,其半长轴衰减较慢,在半长轴衰减观测量时应扩大时间间隔。
在后续工作中,计划对不同形状、不同高度及不同太阳活动条件下的航天器弹道系数进行解算,分析该方法在不同条件下的适用性。

