借助观察和操作感悟旋转本质
李先春 黄劲松

《图形的旋转》是人教版数学五年级下册第五单元的教学内容,本课时要在学生初步认识生活中的旋转现象的基础上,引导学生借助钟面、线段、三角形等图形的旋转,感悟旋转的本质。
一、借助钟面,明确旋转三要素
五年级学生仍然需要借助生活实例认识旋转。因此,笔者在教学中注重选取生活中的典型例子,丰富学生的认知,让学生充分感知旋转现象。
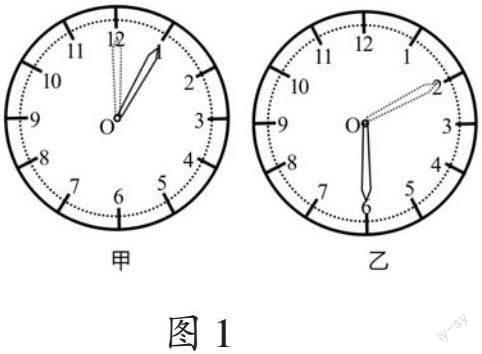
上课伊始,笔者呈现钟面、纸风车、道闸、秋千4个场景,并设疑:“你能从4个场景中发现旋转运动吗?它们是如何旋转的呢?”一名学生说:“钟面和纸风车是旋转现象,钟面上的指针是从右上方向下转,然后向左转,再转回到上方;纸风车旋转的方向与钟面上指针的旋转方向相反;道闸和秋千的场景中没有旋转运动。”笔者顺势总结:“钟面上指针旋转的方向是‘顺时针方向,与指针旋转方向相反的方向是‘逆时针方向,由此可知,现实生活中物体的旋转都是有方向的。”接着,笔者用课件出示钟面(如图1),动态演示指针从“12”旋转到“1”(如图1甲),再从“2”旋转到“6”(如图1乙),并设疑:“两个钟面上指针的旋转过程有什么不同?”
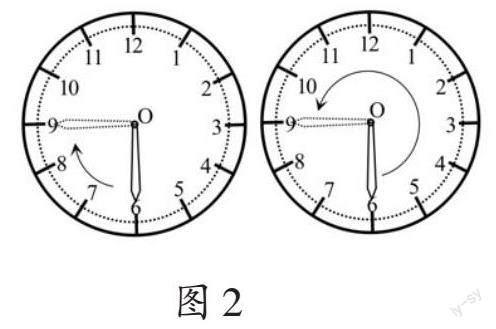
一名学生说:“指针旋转的起始位置不同,旋转的角度也不同。”笔者追问:“甲、乙两个钟面上指针的旋转过程有什么相同点呢?”他接着说:“指针旋转的方向都是顺时针旋转,指针旋转的中心也相同。”“指针从‘12旋转到‘1,该怎样用语言描述?”笔者继续引导。又一名学生说:“指针绕点O顺时针旋转了30ο。”最后,笔者让学生想象指针从“6”旋转到“9”的过程(如图2)。
经过思考后,又一名学生说:“指针从‘6绕点O顺时针旋转90ο到‘9。”笔者追问:“还可以怎样描述?”他接着说:“也可以说指针从‘6绕点O逆时针旋转270ο。”笔者总结:“指针从某一点旋转到另一点,可以说按顺时针方向旋转,也可以说按逆时针方向旋转,此时顺时针旋转的角度与逆时针旋转的角度的和是360o。”
经历对钟面的观察、想象、描述等活动过程,学生进一步理解了旋转的含义,初步体会到图形旋转的基本要素是旋转中心、旋转方向和旋转角度,为后面学习旋转的性质做了铺垫。
二、借助操作,感悟旋转的本质
此环节,笔者以“线段”为研究对象,让学生从线段的旋转过程中感悟旋转的本质。
教学时,笔者先在方格纸上给出一条线段OA,让学生以小组为单位进行模拟操作,选择某个点为旋转中心,将线段向一个方向旋转90ο,并将旋转后的图形画在方格纸上。学生完成模拟操作后,笔者请学生交流怎样旋转、怎样画出旋转后的图形。第一小组代表说:“我们以端点O为旋转中心,按顺时针方向旋转90ο;画图时先找到端点A的对应点A′,然后连接OA′,如图3(1)所示。”第二小组代表说:“我们以线段OA的中点M为旋转中心,按逆时针方向旋转90ο;画图时先找到端点A的对应点A′和端点O的对应点O′,再连接O′M、MA′,如图3(2)所示。”第三小组代表说:“我们以线段OA的四等分点M为旋转中心,按逆时针方向旋转90ο;画图时先找到端点A的对应点A′和端点O的对应点O′,再连接A′M和MO′,如图3(3)所示。”
笔者肯定了学生的回答并总结:旋转中心可以定在线段的任意一个位置上,画图时要注意旋转的三要素,基本画图步骤为:①确定旋转中心;②将连接旋转中心的边按既定的方向旋转(旋转前后的边长不变),并找到各端点的对应点;③连接对应点和旋转中心。接着,笔者用课件呈现图3(4)、图3(5),并设疑:“这两个图形是线段OA经过怎样的旋转后形成的?”第四小组代表说:“图3(4)是线段OA绕端点A顺时针旋转90ο后形成的图形;图3(5)是线段OA绕四分点M逆时针旋转90ο后形成的图形。”最后,笔者组织学生观察图3(1)~图3(5),并思考:线段旋转的过程中,什么变了、什么没变?学生观察、交流后,发现线段旋转前后的形状和大小不变,即对应点到旋转中心的距离不变;线段的位置和方向发生了改变;旋转中心点是唯一不动的点。
经历了线段旋转的操作过程,学生对旋转要素的理解更深了。
三、借助應用,欣赏旋转运动的美
图形的旋转是图形上的每个点在平面上绕某个固定点旋转固定角度的位置移动,相对于图形的平移,图形的旋转更加复杂。教学时,笔者呈现例2(如图4),引导学生将三角尺在方格纸上每次按顺时针方向旋转90ο,观察三角尺的位置是如何变化的。
笔者先让学生用三角尺在画好的方格上按要求旋转,并记录每次旋转后三角尺的位置,观察、思考旋转前后三角形的位置是如何变化的。一名学生说:“我发现旋转时点O的位置始终不变。”另一名学生补充道:“我发现三角尺两条直角边都绕点O按顺时针方向旋转了90ο。”笔者追问:“斜边又是如何变化的呢?”他接着说:“也是绕点O顺时针旋转90o。”“在三角尺旋转的过程中,什么变了、什么没变?”笔者接着设疑。“旋转中心的位置不变,且过旋转中心的所有边的旋转方向、旋转角度相同,即旋转后三角尺的形状、大小都没有发生变化,只有位置变了。”笔者顺势总结:旋转前后的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心连线所成的角也相等。
接着,笔者引导学生完成“做一做”:换另一把三角尺,在方格纸上按逆时针方向转一圈,旋转后变成了一个什么图案。学生操作后汇报:“三角尺按上述方式逆时针旋转,会得到一个风车图案(如图5甲)。旋转后三角形的形状、大小都没有变化,只有位置变了。”笔者组织学生将例2进行变式旋转,把三角尺绕锐角顶点顺时针旋转一圈,让学生画出旋转后的图案,并将图案涂上自己喜欢的颜色,然后展示交流。学生操作三角尺旋转、画图并展示后,笔者用课件呈现学生创作的优秀图案(如图5乙)。
学生经历图形的旋转过程,不仅完善了对旋转性质的认知,而且欣赏到图形旋转后形成的美丽图案,感受到图形运动的美,体会到数学的应用价值。
(作者单位:李先春,应城市杨岭镇中心小学;黄劲松,应城市实验小学)
责任编辑 张敏

