考虑消费者耐心程度与企业成本削减的产品定价策略
官振中, 杜华峰, 何三明
(西南交通大学 经济管理学院,四川 成都 610031)
0 引言
在新冠肺炎疫情导致全球经济遭受逆流的背景下,2020年我国双十一购物狂欢季的全网交易额接近8600亿元,同比增长43.3%,再创历史新高。巨大交易额的背后,一方面彰显了我国内需市场的强大动能,另一方面反映了消费者会事先通过互联网等科技手段获取及时、准确的产品信息(如价格信息、当月订单量等),并在此基础上形成对未来价格的理性预期,进而做出最佳购买决策。当预期心仪产品在双十一期间出现大幅降价或折扣时,消费者会延迟自己的购买行为,表现出高度耐心并愿意等待至活动当天再购买。通常将这类“聪明”的消费群体称为策略型消费者。若忽视这类消费者的延迟购买行为,企业的利润流失高达20%[1]。可以看出,科技的发展为消费者提供便利的同时,也为动态定价策略的实施带来诸多阻碍。因此,企业需选择适当的定价策略来有效缓解消费者的等待行为,差价补偿就是其中策略之一。通过承诺产品降价后,对先前购买产品的消费者进行差价退还,以吸引更多消费者提前消费,进而有效阻止潜在利润的流失。
此外,为提高市场竞争力,企业往往会运用业务流程重组、生产技术变革等手段降低生产成本。例如,Apple公司通过调整运营模式降低与制造商的交互成本,进而达到精简成本、提高收益的目的。为此,在“价格透明化”的市场环境下,探讨消费者耐心程度与企业成本削减对产品定价策略选择的影响,具有一定的研究价值。
与本文较为相关的研究领域主要涉及两个方面:(1)基于策略型消费者的定价研究;(2)企业的成本削减问题。近些年,国内外基于策略型消费者的定价研究已有较为丰硕的成果。例如,PAPANASTASIOU等[2]研究了社会学习对垄断企业最优定价与利润的影响。ZHAO等[3]研究了价格参考效应对最优定价策略选择的影响。PARLAKTÜRK等[4]面向策略型消费者,研究了企业提供垂直差异化产品的价值。国内学者官振中等[5]将消费者策略行为与参考效应相结合,探讨了企业最优定价问题。蒋敏等[6]通过构建差价补偿策略下的Stackelberg博弈模型,研究了供应链上下游之间的协调优化机制。这些研究主要侧重于探讨单一定价策略或多种定价策略下消费者行为对企业最优决策的影响,但较少有文献将企业成本削减与消费者耐心程度相结合。
在成本削减的研究中,LIN等[7]讨论了第二销售期成本下降幅度及其不确定性对双边垄断平台定价的影响。HA等[8]基于竞争供应链,研究了制造商成本削减对零售商需求信息共享的影响。SHUM等[9]基于科技进步和生产学习,探讨了成本削减对企业最优定价策略选择的影响。杜华峰和官振中[10]将消费者行为和企业成本削减相结合,探讨了垂直差异化产品的推出策略问题。上述研究主要考虑成本削减对产品最优策略或供应链信息共享的影响,然而较少有文献同时涉及定价策略、消费者耐心程度以及企业成本削减的情形。
与上述研究相比,本文分别在动态定价策略和差价补偿策略下,综合考虑消费者耐心程度与企业成本削减对产品定价策略选择的影响,并探讨两种定价策略的优劣性。与此同时,本文还将模型拓展到策略型消费者具有价格参考效应的情形,以讨论最优决策是否依然成立。
1 问题描述
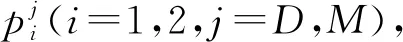
ui=δi-1(v-pi)(i=1,2)
其中,δ(0<δ<1)为时间贴现因子,也可理解为消费者耐心程度,δ越大,说明消费者越有耐心。
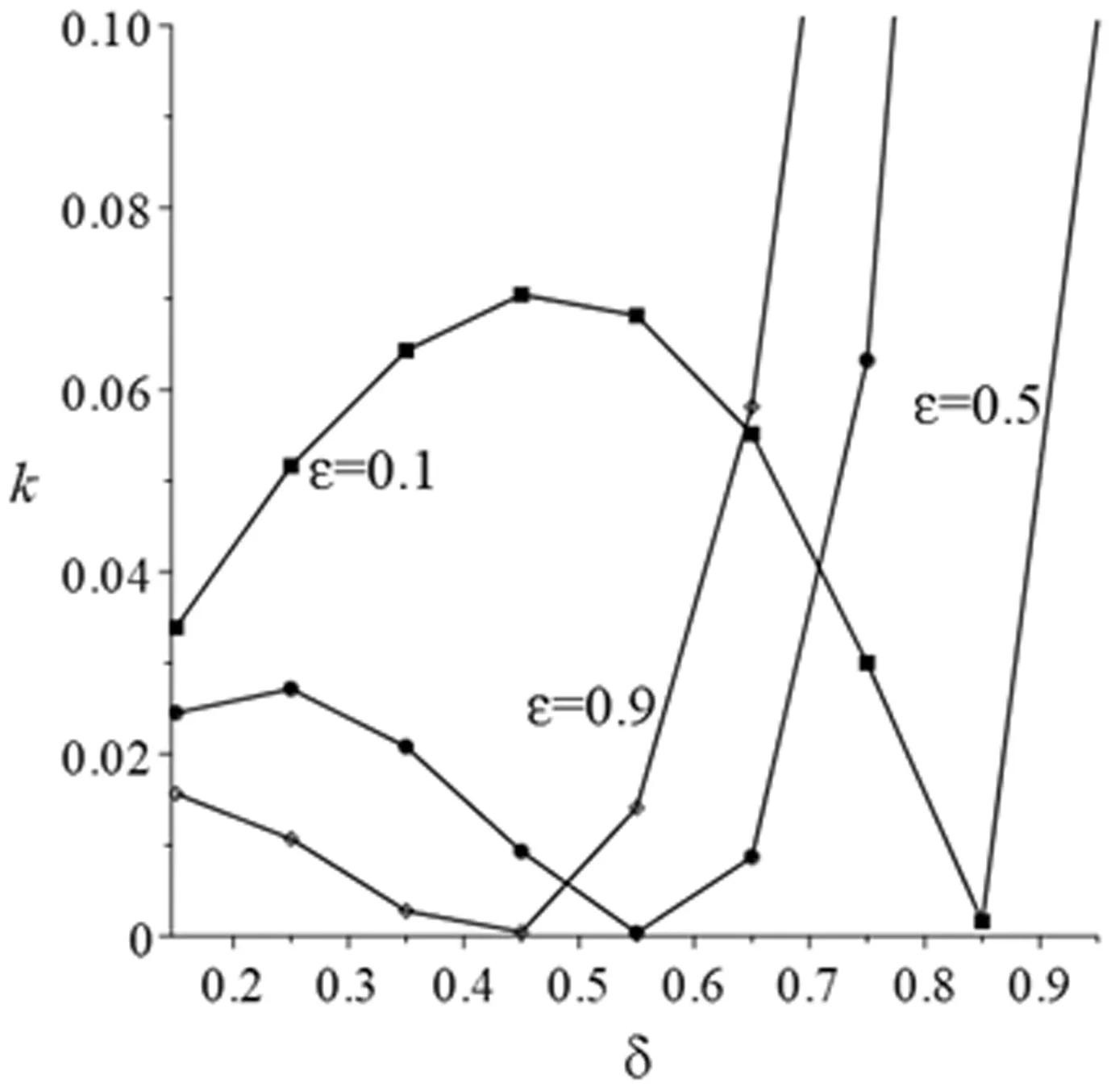
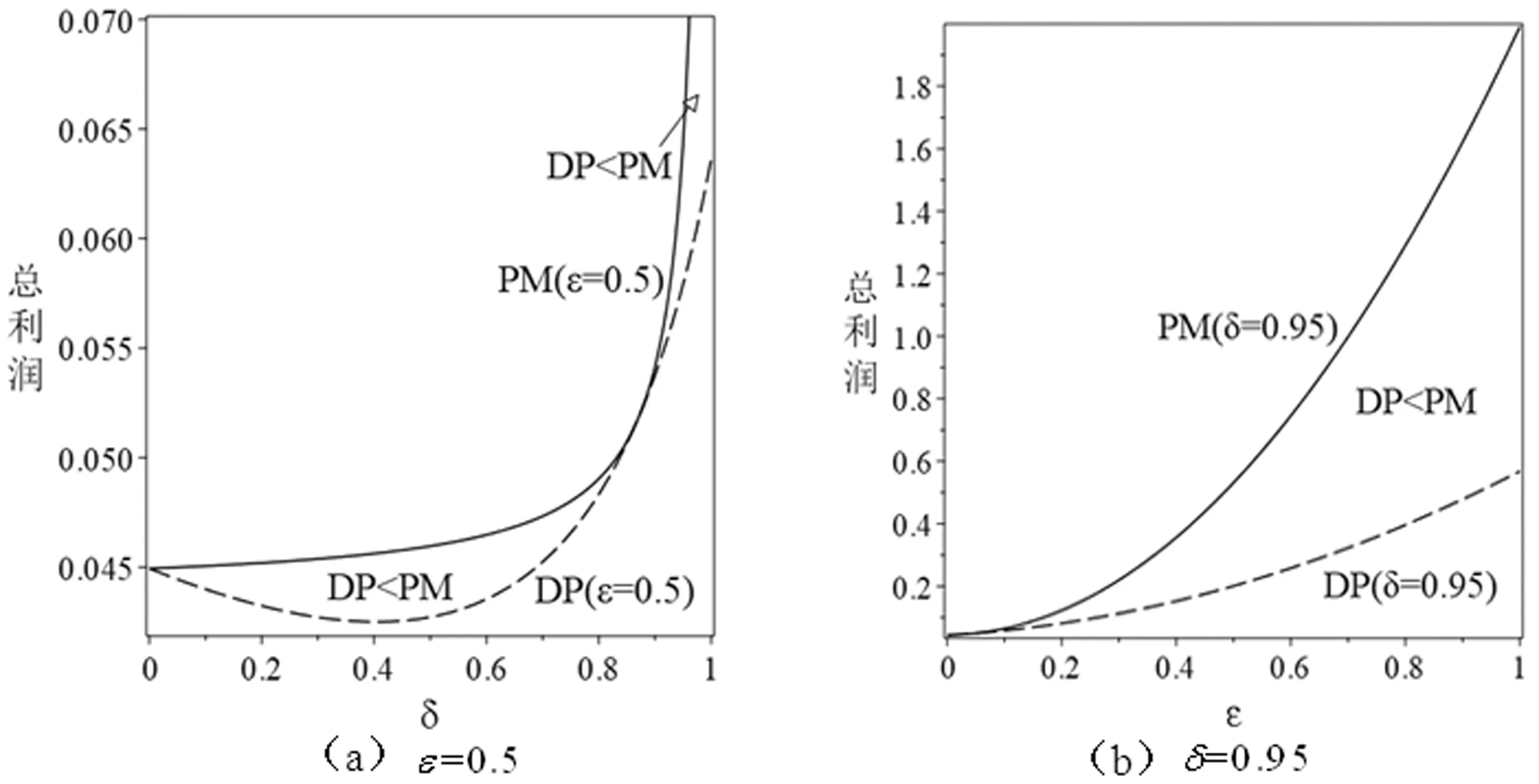
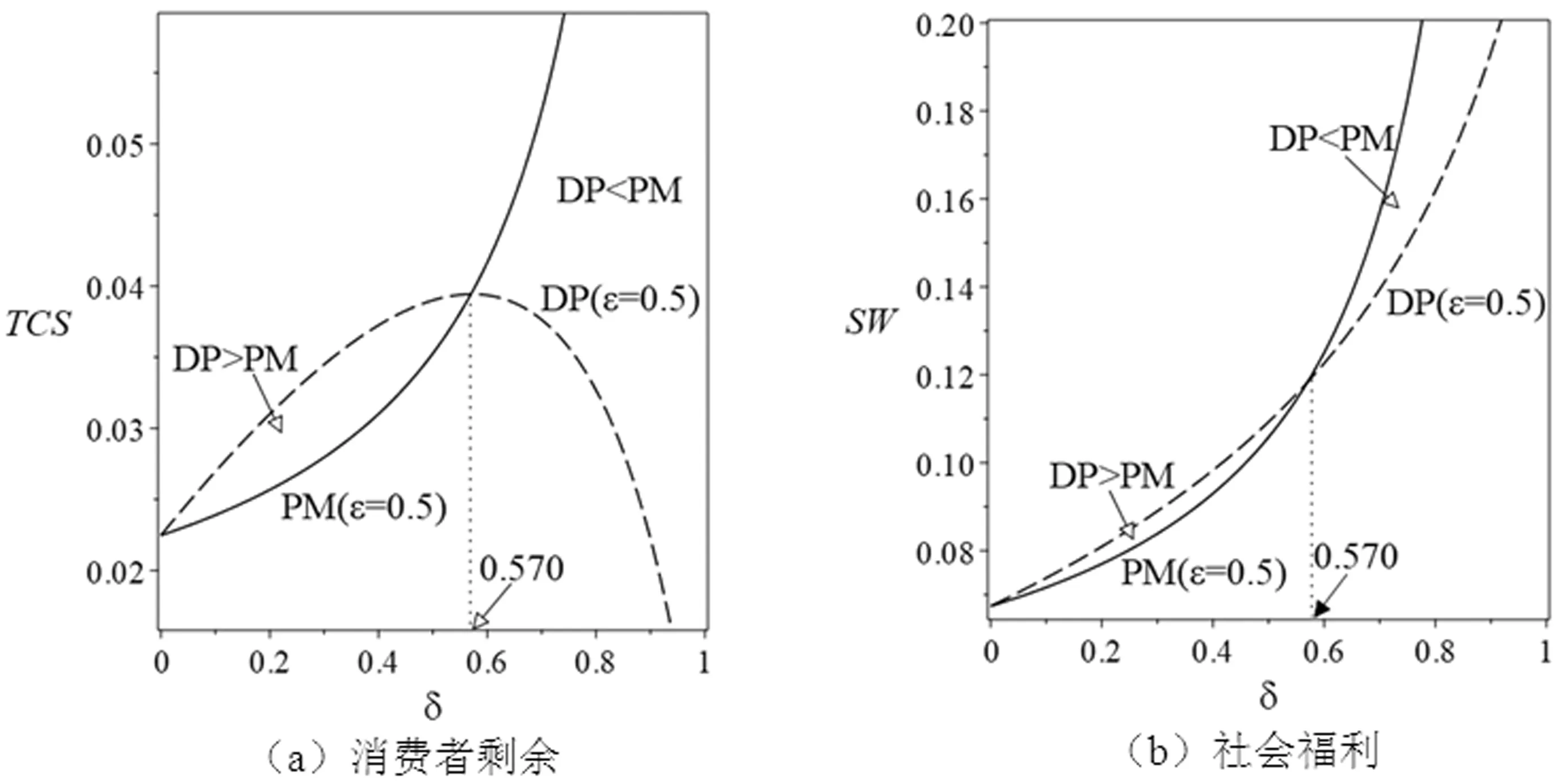
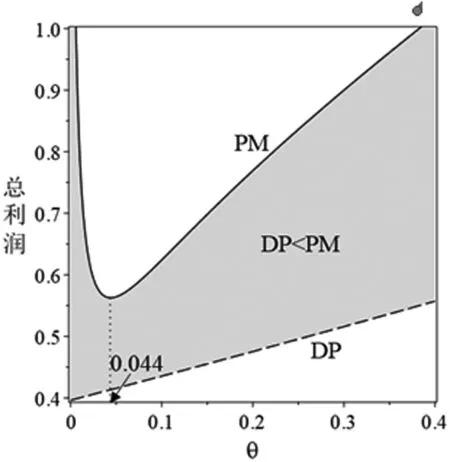
由于科技进步与业务重组等多方面的综合影响,企业在第二阶段存在成本削减。假设削减幅度为ε(0<ε<1),则第一阶段和第二阶段的生产成本分别为β2q与(β-ε)q2。其中,q为产品质量水平,β为单位质量成本系数,且满足0<β 求解可得: 此时,企业在第二阶段的利润函数为 两阶段的总利润函数为 命题1动态定价策略下,两阶段的最优均衡为 πD*=[δε2q4(4+δ)+(2-δ)2+q4(β2(2-δ)2-2βδ2ε)- 2q2(β(2-δ)2-δ2ε)]/[4(4-3δ)] 命题1表明,第一阶段产品均衡价格始终高于第二阶段产品均衡价格(即撇脂定价策略)。同时,当成本削减幅度越小或消费者耐心程度越大时,产品价格差越小。 其中, 命题2(1)表明,当δ较小时,第一(二)阶段产品价格与ε呈正(负)相关。ε越大,第一阶段产品价格越高,企业攫取高支付意愿群体的消费者剩余越多。与此同时,企业将第二阶段产品价格设置在一个较低的水平,以抢占价格敏感型消费者的市场份额。当δ较大时,消费者的策略行为愈加凸显,此时较大的成本领先优势促使企业提高第二阶段产品价格。 命题2(2)表明,当δ较小时(如图1中区域III),消费者更倾向于第一阶段购买。此时,随着δ的增大,适当提高产品价格可以使企业在较大范围内攫取消费者剩余,进而转化为自身收益。当δ较大时(如图1中区域I和区域II),消费者行为更加具有策略性与选择性。此时,第一阶段产品价格与δ之间的变化关系还受到ε的影响。具体来说,若ε较小(较大),随着δ的增大,企业应降低(提高)第一阶段产品价格。另外,无论ε如何变化,随着δ的增大,提高第二阶段产品价格均可以抑制消费者的策略等待行为。 两阶段的总利润函数为 命题3差价补偿策略下,两阶段的最优均衡为 命题3表明,差价补偿策略下,产品价格差与成本削减幅度或耐心程度均呈正相关。这与动态定价策略下的研究结论不完全相同。 命题4(1)表明,随着ε的增大,企业会提高第一阶段产品价格,以在短期内达到盈亏平衡点。在第二阶段,企业会降低产品价格。一方面,是为了争夺价格敏感型消费者的中低端市场份额,进而提高市场占有率;另一方面,差价补偿机制的存在会促使消费者提前购买产品,而不再顾虑产品未来价格走势,即第二阶段的产品需求会部分转移至第一阶段。此时,企业在第二阶段采取降价手段可以有效避免销售期结束时库存产品挤压而带来的潜在利润流失。 命题4(2)表明,随着δ的增大,企业会在第一阶段设置较高水平的产品价格。这是因为,差价补偿策略下,消费者不再具有策略性等待行为。因此,企业会将第一阶段产品价格提高至消费者的保留价格附近,以获得最大利润。同时,由于差价补偿策略可以完全消除消费者的策略等待行为,进而使得企业在第二阶段产品定价过程中不会考虑消费者耐心程度的高低,即第二阶段产品价格独立于消费者耐心程度。 命题5πD*<πM*。 命题5表明,在同时考虑耐心程度和成本削减幅度的前提下,差价补偿策略对企业更有利。引入利润差系数k=(πM*-πD*)/πM*,其中k也可以反映差价补偿策略相较于动态定价策略的利润改进幅度。显然,k越大,差价补偿策略对利润的改进幅度也就越大。图2展示了δ与k的关系。图形显示,当ε较小时(如ε=0.1),k随δ的增大呈先增后减再增的趋势。当ε较大时(如ε=0.9),k随δ的增大呈先减后增的“U”型变化趋势。这是因为,当成本削减幅度处于不同水平时,随着δ的增大,两种定价策略下的总利润变化趋势不同步,即总利润的变化速率不尽相同。 图2 δ与k的关系 接下来,将分别求解两种定价策略下的消费者剩余(TCS)和社会福利函数(SW),分别为 SWD*=TCSD*+πD* SWM*=TCSM*+πM* 命题6当0<δ<δ2时,TCSD*>TCSM*,SWD*>SWM*;当δ2≤δ<1时,若0<ε<ε2,则TCSD*>TCSM*,SWD*>SWM*;若ε2≤ε<1,则TCSD*≤TCSM*,SWD*≤SWM*。 命题6表明,当δ较小或δ较大且ε较小时,动态定价策略对于消费者或整个社会来说是有利的。当δ和ε均较大时,差价补偿策略不仅使企业受益(命题5),而且对消费者或整个社会来说都是有效率的。 图3(a)给出了耐心程度对总利润的影响。图形显示,差价补偿策略下的总利润随δ的增大呈递增趋势,而动态定价策略下的总利润随δ的增大呈先减后增的“U”型变化趋势。这是因为,动态定价策略下,随着δ的增大,第二阶段产品价格随之提高,虽然会导致部分消费者离开市场而损失一部分利润(即负效应),但可以在一定程度上缓解消费者的延迟购买倾向,进而改善企业的经营利润(即正效应)。因此,动态定价策略下,总利润与δ的关系取决于正、负效应的相对强弱。此外,成本削减幅度对总利润的影响如图3(b)所示。图形显示,两种定价策略下的总利润与ε之间均呈正相关。 图3 δ和ε对总利润的影响 图4展示了δ对消费者剩余和社会福利的影响。图形显示,TCSM*随δ的增大呈递增趋势,而TCSD*随δ增大呈先增后减的“倒U”型变化趋势。同时,社会福利随δ的增大而增大。这与命题6的研究结论相吻合。 图4 δ对消费者剩余和社会福利的影响 本节将考虑策略型消费者具有价格参考效应的情形。为便于后续表述,上标R表示消费者具有价格参考效应时的相应变量。若θ(0<θ<1)为消费者依赖参考价格的程度,则第二阶段的净效用函数为 其它模型构建过程与正文类似,此处不再赘述。图5给出了价格参考效应下的最优定价策略选择。当考虑价格参考效应时,总利润在差价补偿策略下始终较优,这与正文结论是一致的。同时,图形还表明,差价补偿策略下,总利润随着θ的增大呈先减后增的“U”型趋势。然而,动态定价策略下,总利润随着θ的增大而增大。 图5 θ对总利润的影响(ε=0.8,δ=0.95 ) 针对企业定价策略的最优选择问题,本文分别构建了动态定价策略和差价补偿策略下的两阶段博弈模型,并对比分析了两种定价机制的优劣性。同时,本文在拓展部分还考虑了价格参考效应。研究发现,当考虑策略型消费者和成本削减时,差价补偿策略仍然能提高整体收益水平。其次,虽然动态定价策略会导致潜在利润的流失,但在一定条件下,对消费者或整个社会来说都是有利的。最后,价格参考效应并非在任何情况下对企业来说都是不利的,还受到定价策略与参考效应强度等因素的联合影响。 未来研究可以考虑消费者等待成本等情形,以丰富模型使用场景。2 模型构建与求解
2.1 动态定价策略(DP模型)
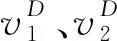
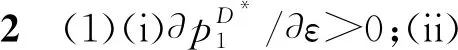
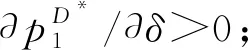
2.2 差价补偿策略(PM模型)
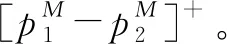
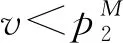
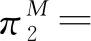
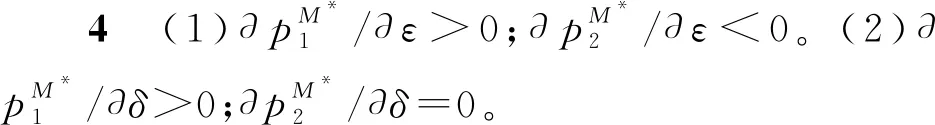
3 定价策略的对比分析
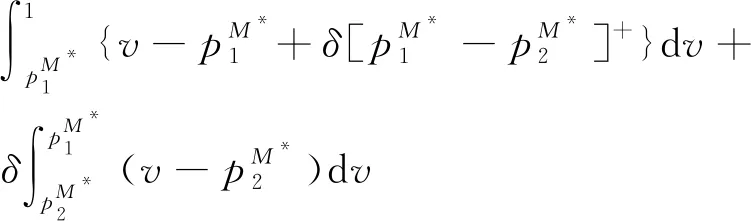
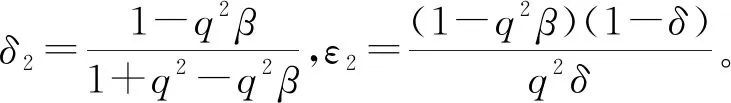
4 数值仿真分析
5 拓展研究
6 结论

