一类区间值时间序列IO型异常点检测方法 及其在金融时序分析中的应用
陶志富, 冯浩洋, 陈华友,2
(1.安徽大学 大数据与统计学院,安徽 合肥 230601; 2.安徽大学 数据融合与开发应用中心,安徽 合肥 230601; 3.安徽大学 金融与统计研究中心,安徽 合肥 230601)
0 引言
随着社会的发展,海量和瞬时数据使得准确把握现实观测对象的时间序列观测值变得困难。自从MOORE提出区间分析以及BILLARD和DIDAY开创符号数据研究以来,区间值数据为解决上述困难提供了有效分析工具。实际上生活中普遍存在一些区间型的数据,如:一天中股票的开盘价和收盘价、气温的变化、空气污染浓度等。将原始数据汇总为单个值可能意味着相关的信息丢失,因此区间值时序分析成为近年来国内外备受关注的研究热点。
区间值时间序列分析主要包括预测原理和方法的构建、特征分析[1]以及应用三个方面。其中,预测原理和方法的构建又可以具体划分为基于统计分析[2]、模糊工具[3]、人工智能原理[4]和混合模型[5]等预测技术。BILLARD最早从数据中心对区间数据进行预测模拟,后又提出最大值和最小值法,对区间的上下界分别建立回归模型进行区间模拟和预测。NETO等[6]提出了中点与极差法,并且通过蒙特卡洛模拟,得出中心和极差法预测效果要比BILLARD的最大值和最小值法好。MAIA等[7]直接从区间出发,应用自回归(AR)和自回归移动平均(ARIMA)模型以及神经网络等建立区间型时间序列分析模型。HAN等[8]提出一种具有外生解释区间变量(IVARMA)的区间时间序列过程的简约自回归模型。可以看出,将区间值时序通过上、下限或中心、半径视角划分为点值时序以及以区间整体形式代入计算的区间计量模型成为当前区间值时序分析主要模式。
应用方面,杨威等[9]从区间时间序列出发,利用美国股市和中国股市的数据研究发现区间时序模型比传统的点值AR模型和VAR模型更具稳健的预测优势,因此对于区间型时间序列建模研究是非常有必要的。
点值时间序列分析过程中,异常值的存在对预测精度会产生重要影响[10]。类似地,以2020年4月22日美原油2005合约价跌破负值异象为例。区间值时间序列,特别是金融时序也存在异常值情形。因此,检测并处理异常值对区间时间序列预测建模同样具有重要意义。
针对点值时间序列,Fox(1972)最早将时间序列异常点分为加性异常点(Additional Outlier, AO)和革新异常点(Innovative Outlier, IO),后有学者在此基础上又补充了三种前两者变形的异常点水平位移异常点(Level Shift, LS)、暂时变化异常点(Temporary Change, TC)和斜线上升异常点(Ramp Effect, RP)。在性质上后三者其实是AO和IO的特例,一般认为时间序列中最基本的异常点就为AO和IO两类异常点。对于点值时间序列异常值的检测,已经出现了很多的异常检测算法。常见的有基于统计模型[11]的异常点检测方法、基于聚类的异常点检测方法[12]和基于机器学习[13]的异常点检测方法。但是,目前鲜见有关区间值时间序列异常检测的相关报道。因此,针对金融行业区间价格等数据直接影响投资者预期进而可能改变投资行为的特征,因而异常值更容易造成对后续序列产生影响,本文在现有点值时间序列IO型异常值检测的方法上,定义了区间型IO型异常区间的概念以及给出了检验原理和算法。最后,应用上证综指区间观测数据进行了实例验证。结果表明,所提出的方法能够较好的识别到区间型时间序列中的IO型异常区间。
1 预备知识
1.1 区间值时间序列
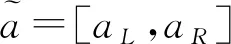
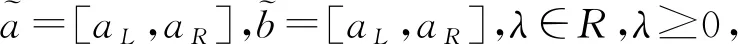
依据上述减法运算,对∀β∈R,我们有βa+(-β)a=[βaL-βaL,βaR-βaR]=[0,0]。
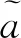
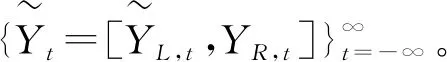
1.2 一类稳健的IO型异常点检测
点值时序{Yt}对应ARMA(p,q)模型如下:
(1)
其中εt是一个零均值的白噪声。
由文献12可知,在点型时间序列IO型异常点检验中,如果时间序列只在时刻T发生IO型异常,那么用于检测时刻T的检验统计量为:
λT=eT/σ
(2)
其中eT表示模型(1)在T时刻的残差,σ表示模型(1)所有残差的标准差。
在满足零假设没有异常点时,检验统计量(近似)服从标准的正态分布。在T事先已知且确定观测量为IO型异常点的情况下,对应的标准差大小在的显著性水平下不能超过。但现实中往往没有时刻T的先验知识,因此需要对所有的时刻t进行检验,另还需对σ进行估计。对所有时刻t的多重检验,对其整体误差控制最简单有效的方法为应用Bonferroni律,令
(3)
这里,n表示时间序列的观测期数。
若异常值仅在T时刻开始发生,最大值在t-T时刻取得,此时若λ1超过正态分布上百分位数0.025/n×100,则拒绝原假设,认为时间序列T时刻的观测值为IO型异常点。Bonferroni律保证了错误认定IO型异常概率最大为5%。
可见对于T时刻IO型异常值检测主要是检测统计量λT取值,而λT取值大小由eT和残差的标准差σ所决定。但残差σ的大小往往受到异常点影响,IO型异常点的存在会使得σ取值变大,从而极大地影响了检测的准确性。因此文献12采用了σ的更稳健估计量即绝对离差均值。对于绝对离差均值的定义为:
(4)
其中xi为总体X中的第i个观测值,MED(X)表示中位数。
采用离差均值有效的避免了IO型异常值检测过程中的“淹没”现象和“掩盖”现象。
因此检验统计量可最终表示为:
(5)
2 理论研究过程
2.1 区间型时间序列IO型异常区间概念
革新异常点(IO)通常涉及到时间序列内在相关结构,故往往是成片出现的,即出现一个IO,由于相关性使得它后续点也表现出一定的异常。
点值时间序列IO型异常本质上可以归纳为时序数值水平一定时期持续的规律性变化。区别于点值时序,区间值时序的数值水平受到上、下限序列或中心、半径序列共同作用。由于中心、半径序列能够综合上、下限序列作用,为此本文从中心、半径序列视角进行分析。
从数的拓展角度,当区间数的上、下限相等时,区间数退化为普通的点值。反之,点值时间序列可以视为区间下限和上限一致的特殊区间值时间序列。因而,当这一特殊区间值上、下限数值水平发生波动时易知出现以下3种情形:
情形1上、下限数值水平发生同向变化,表现为中心序列数值水平发生变化,半径序列数值水平保持相对不变;
情形2上、下限数值水平发生反向变化,表现为半径序列数值水平发生变化,中心序列数值保持水平相对不变;
情形3上、下限数值水平仅有一个发生变化,表现为中心和半径序列数值水平同时发生变化。
因而,区间值时序数值水平异常变化可以归纳为中心或者半径序列两个点值序列数值水平的异常变化。基于文献14,类似给出区间值时间序列IO型异常的三种特殊表现:
(1)水平漂移
当某时刻的区间发生水平漂移异常时,具体表现为区间中心或区间半径或两者同时突然增加(或减少,即反向增加)到某一新的数值水平且保持这一水平。从金融时序角度即金融产品平均价格或价格波动的数值水平发生变化。
类似点值时间序列水平漂移的数学表达[14],图1所示的区间值时间序列突然增加情形下考虑区间中心和区间半径水平漂移的数学描述为:
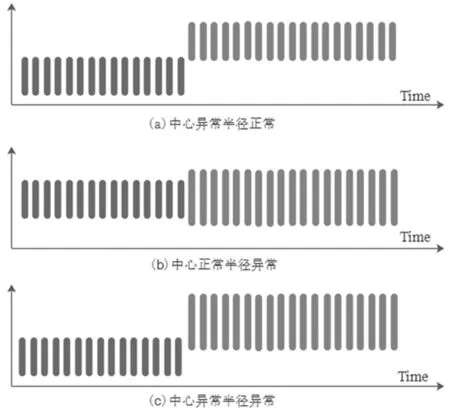
图1 区间值时序数据水平漂移型异常点
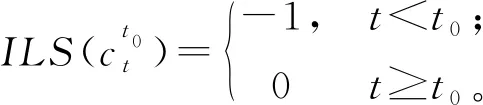
(2)暂时变化
当某时刻区间发生暂时变化异常时,其表现形式为中心或半径或者两者同时突然增加(或减少,即反向增加)到某一水平并且随着时间的变化这种异常逐渐的减少,最终恢复正常趋势。
类似地,图2所示的区间值时间序列突然增加的暂时变化可以表示为:
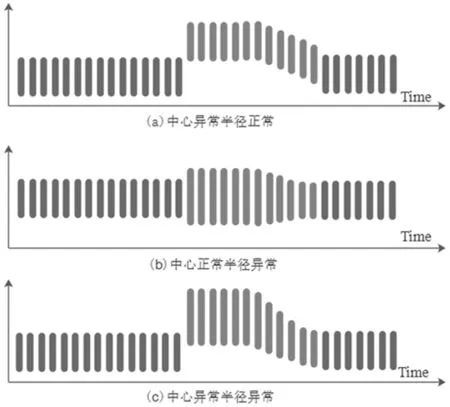
图2 区间值时序数据暂时变化型异常点
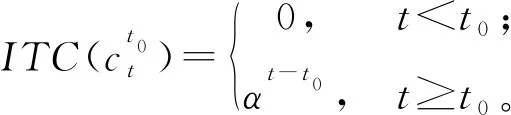
(3)斜线上升
某时刻的区间发生斜线上升异常时,具体表现为中心或半径或者两者同时呈渐变式增长(或减少,即反向增加)到某一水平且保持这一水平。
同理,图3所示的区间值时间序列突然增加的渐变式上升可以表示为:
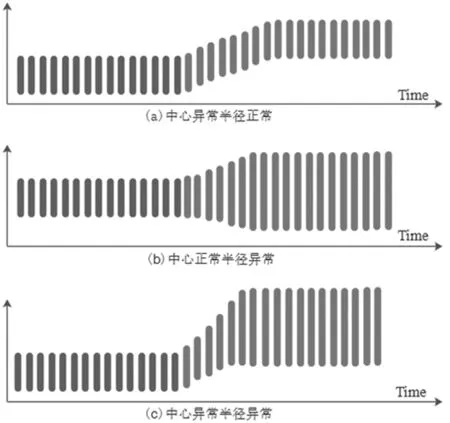
图3 区间值时序数据斜线上升型异常点
其中,
结合传统点值时间序列IO型异常点定义,以下结论是直接的。
定理1当区间值时间序列退化为点值时间序列时,式(6~8)给出的区间型异常点同时退化为点值时序的异常点。
2.2 区间值时序IO型异常点检测原理
区间值时序IO型异常点检测步骤如下:
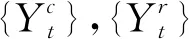
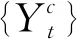
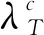
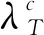
3 实证分析
3.1 数据来源和描述性统计
为探究区间型时间序列IO异常点检测有效性和可行性,选取上证指数日数据作为实例探究,采样区间为2016年1月4日到2018 年12月28日。上证指数每日最低价和最高价构成区间型时间序列。运用2.2节中所提方法对上证指数区间时间序列进行IO型异常区间的检测。
首先将区间型数据进行预处理,把区间型金融时序转化为中心和半径形式,图4和图5分别描述了预处理之后中心和半径走势。
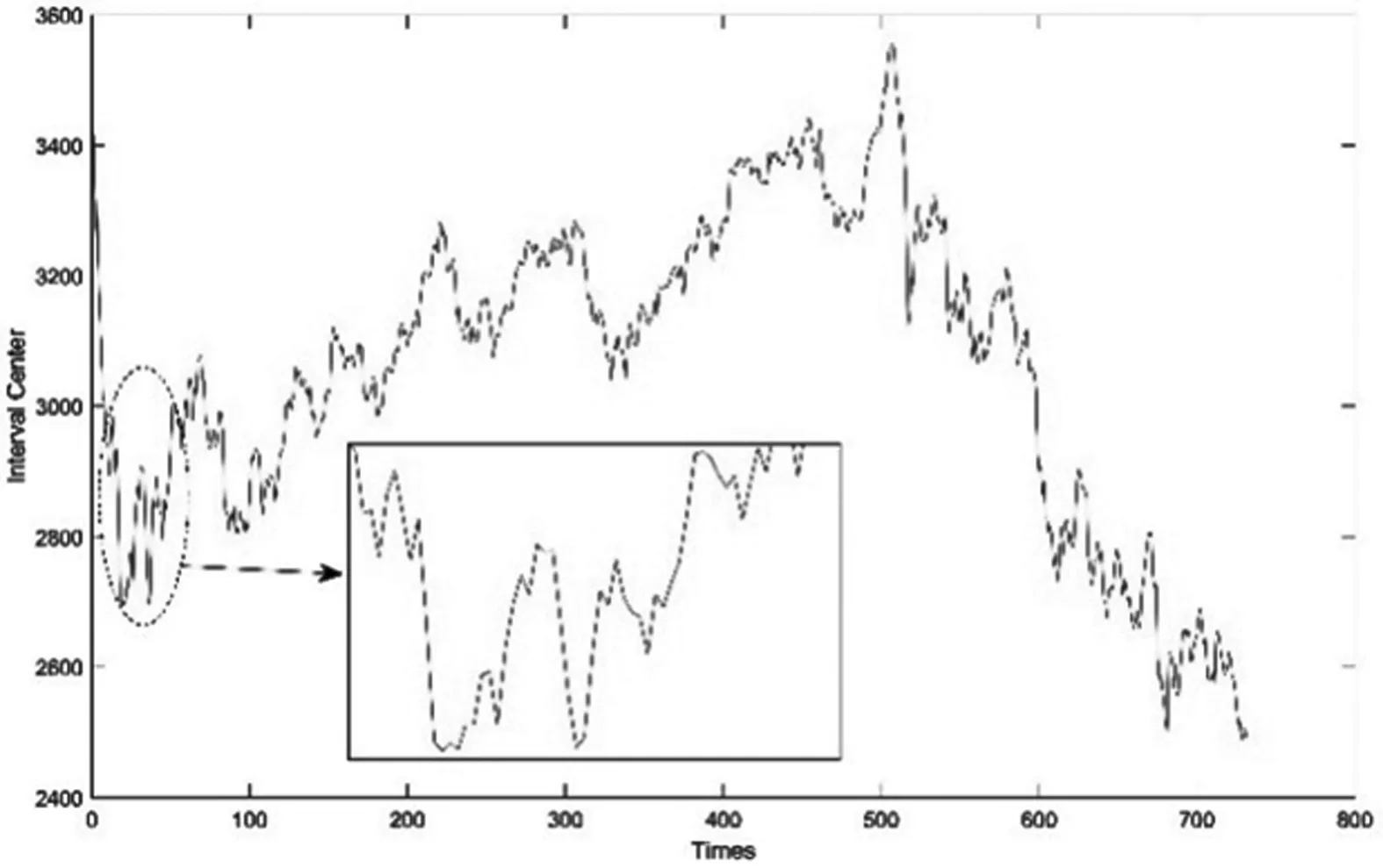
图4 上证综合指数观测区间值时序中心序列图
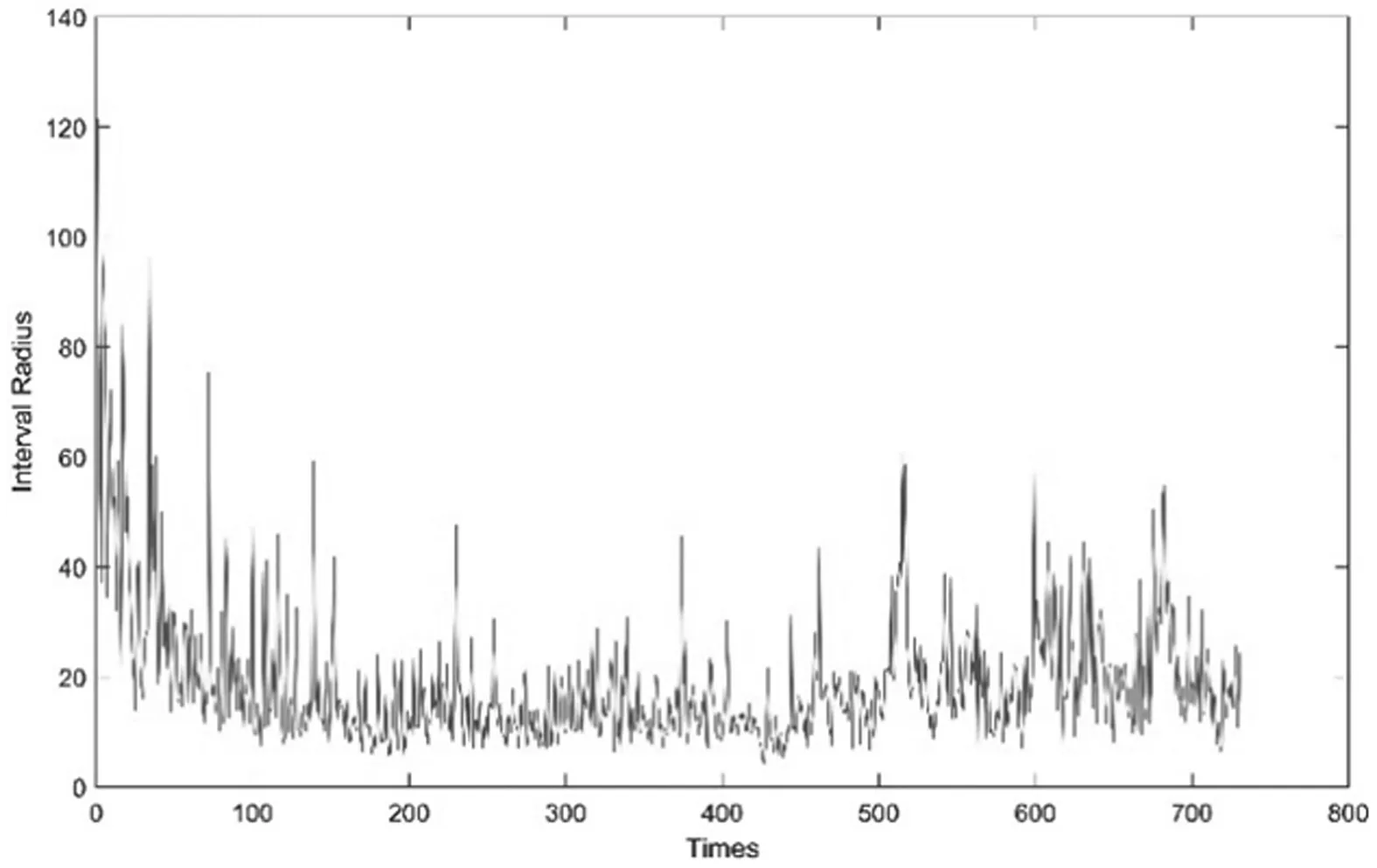
图5 上证综合指数观测区间值时序半径序列图
由图4局部放大图可以看出,区间中心序列存在多处可识别的由较高(或低)水平持续下滑(或上升)到较低(或高)水平的情形,因而是可能的斜线上升型异常。由图6也可看出区间时间序列也存在区间范围或者区间整体水平突然由较高(或低)水平持续下滑(或上升)到较低(或高)水平的异常情况。
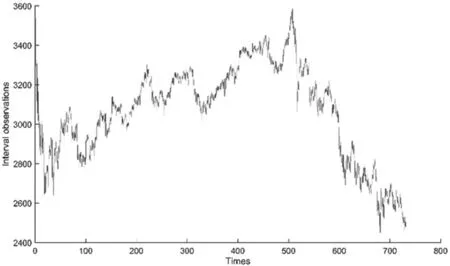
图6 上证综合指数观测区间值时序数据图示
从区间中心序列走势和区间半径序列的变动情况看,2016年上证综合指数有较大的波动,可以初步判断这一年可能存在较多的异常区间。
表1给出了中心和半径的描述性统计分析结果。从表1中可以看出区间中心呈现中等左偏、扁平分布,区间半径呈现出高度右偏、尖峰分布,由于有异常区间的存在使得区间半径变化波动较大,因此有必要对数据进行异常区间的检测。

表1 描述性统计表
3.1 异常点检测
对区间中心和区间半径分别应用进行建模,得到:
其中ΔY1、ΔY2分别表示区间中心和半径差分后的序列且
W1=(0.6397,-0.0346,0.0202,-0.0635)T
W2=(-0.4663,0.0970,0.0999,0.1288)T
θ=(ΔYt-1,ΔYt-2,ΔYt-3,ΔYt-4)T
Q1=(-0.4976,0)′,Q2=(-0.2967,-0.5114)T
β=(et-1,et-2)T
根据AIC和SBC准则,基于最小二乘估计原理,最终针对中心和半径两个子序列分别建立ARIMA(4,1,1)和ARIMA(4,1,2)模型。对模型残差进行Q检验来诊断模型,结果如表2所示。

表2 不同滞后阶数下模型残差Q检验P值
依据表3,累计检测出28个时点对应的区间观测值出现异常,其中有18个异常区间时间点在2016年。这与一开始对时间序列的趋势分析结果符合。

表3 IO型异常区间检测结果
根据检测出的异常时间点,按照2.1节所给的三种形式异常表现形式,给出符合异常表现的异常时点:2016/1/5~2016/1/7发生斜线上升(反向)异常,2016/1/12发生水平漂移(反向)异常,2016/1/25~2016/1/27发生斜线上升(反向)异常,2016/2/16和2016/2/25发生暂时变化异常,2016/5/6~2016/5/9发生斜线上升(反向)异常,2016/6/24发生暂时变化(反向)异常,2018/2/7~2018/2/9发生斜线上升(反向)异常,2018/10/11和2018/10/22发生暂时变化(反向)异常。
3.2 结果分析
为验证区间值金融时间序列异常区间检测结果的有效性,本节对检测出的28个异常区间从统计意义、实际表现和点值时序异常点检验结果对比三个视角进行分析。
首先,从均值、方差、标准差的角度比较正常区间和异常区间,结果如表4所示。
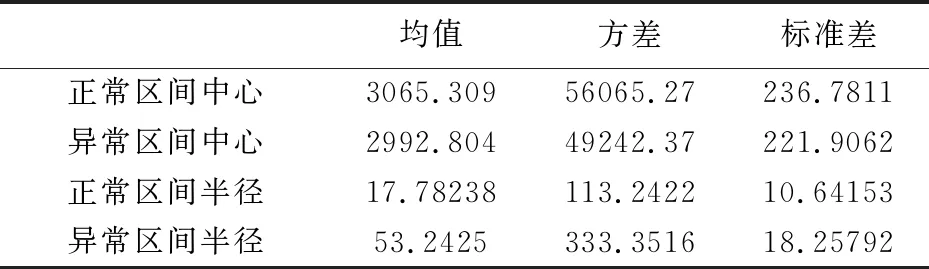
表4 IO型异常区间检测结果
对区间中心和区间半径分别进行均值t检验及方差齐性检验。结果显示区间中心的t检验和方差齐性检验的P值分别为0.099和0.6532,大于0.05,不能拒绝两者相等的原假设,即0.05显著性水平下正常区间中心和异常区间中心均值和方差相等。区间半径的t检验和方差齐性检验的P值分别为2.2×10-6和6.518×10-11,小于0.01,拒绝两者相等的原假设,认为正常区间半径和异常区间半径的方差存在显著性差异。说明检测出的异常区间在区间范围上的波动远大于正常区间,与异常区间的区间范围异常特征相符。
异常区间对应时点上证指数实际表现分析表明:区间值金融时间序列异常区间检测方法是有效的。
作为对比,选取2016年1月4日到2018年12月28日上证指数每日的收盘价构成的点值时间序列数据,按照1.2节所用方法对其检测,最终的检测结果如表5所示。

表5 IO异常时间点检测结果
在点值时间序列IO型异常点的检测中,最终检测出17个异常时间点,其中有11个异常时间点和区间异常检测方法得到的时间点一致,可以确定对应上证指数的实际表现。
在等长时间范围内,区间值金融时序异常点检测输出结果较实值时序确定的异常时点更多,且通过实际数据表现得到了验证,间接地表明区间型数据较实值型数据在金融时序分析中蕴含了更加丰富的信息。另外,采用基于聚类的诊断方法和基于密度的诊断方法对区间数据进行检测,最终异常区间检测结果对比如表6所示。
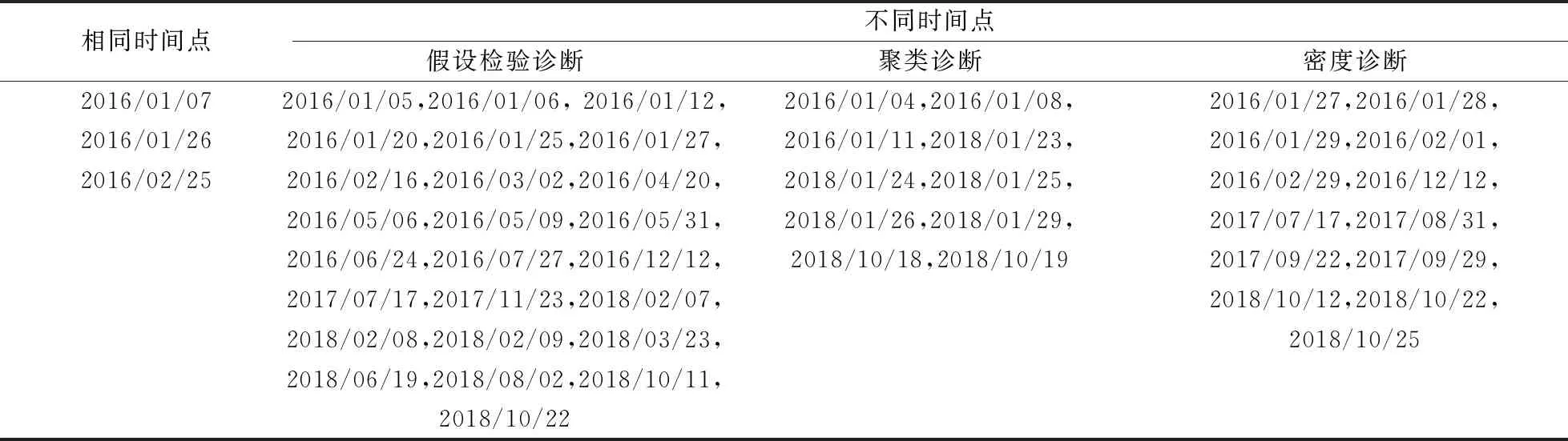
表6 不同检验方法结果对比
如表6所示,三种方法均检测出的时刻上证指数跌幅都在6%以上。由表5和表6可以看出,对比基于聚类分析和基于密度的异常点诊断方法,本文给出的区间值时序异常点诊断能够获得相对更多的异常检验结果,且与其余两种方法的诊断结果在异常点的日期上较为相近,一定程度上反映出不同的诊断方法存在互补性。因而,运用多种检验方法有望提高检测结果的稳健性。
4 结论
时序异常点检测对模型精度影响深远,国内外学者对于异常点检测也进行了大量研究,但大多数学者都是针对点值时间序列,对区间型时间序列的研究甚少。而区间型数据是金融市场中常见的数据类型且其较点值型时间序列蕴含更加丰富的信息,因此本文研究一种针对区间值时序IO型异常点检测方法并应用上证指数数据实证分析。检测结果显示2016年1月4日~2018年12月28日区间上证指数数据包含28个异常区间,其中大多分布于2016年,这与中国股市发展情况相符合,且所提区间异常检测方法基本涵盖了点值时间序列异常检测所输出有效结果,证明所研究方法的有效性和可行性。
下一步,区间值时序异常点检测研究还将进一步从方法拓展、更多类型异常区间检测和异常区间建模三个方面进行进一步研究。其中,区间值时序AO型异常区间的概念界定和检测尚未见具体报道,检测输出结果后如何在预测或者分析模型中进行处理也有待进一步在学理上加以研究。除此之外,类似点值时间序列的异常点检测,不同方法给出的检测结果往往具有一定差异性。因而区间值时序异常点检测原理和方法的稳健性是一个开放性问题。如何构建更加稳健的区间值时序异常点检测方法值得进一步深入研究。

