交互动态直觉模糊前景理论VIKOR法及 在无废城市建设中应用

孟凡永, 蒋 蕾

(中南大学 商学院,湖南 长沙 410083)

0 引言

作为一种新型城市管理模式,“无废城市”建设是中国生态文明建设的一项重大举措,也是实现城市高质量发展的重要内容[1]。“无废城市”建设过程中存在大量复杂决策问题,这些问题涉及多项指标,需要整合多位决策专家的意见,加之“无废城市”建设周期长,决策信息来源于不同时段。因此,采用动态多属性群决策(DMAGDM)方法对“无废城市”建设展开研究显然是十分必要的。

为了有效地刻画模糊评价信息,ATANASSOV[2]提出直觉模糊集(IFSs)的概念。考虑到直觉模糊集的优越性,专家学者们针对动态直觉模糊多属性群决策(DIF-MAGDM)问题展开相应研究。迄今为止,绝大部分研究未考虑动态群决策问题中的交互作用,且相关广义运算法则和算子研究成果较少。而FRANK T模和T余模[3]能退化为ALAEBRAIC T模和T余模,常被用于构建各类模糊运算法则和算子。综上所述,本文定义广义Shapley直觉模糊Frank-Choquet累积算子,对具有交互作用的评价信息进行聚合。

前景理论[4]对决策者有限理性进行了系统性解释说明,被广泛用于群决策中。考虑到当前研究的局限性和直觉模糊特性,本文提出一种基于前景理论的直觉模糊加权决策矩阵构造方法。此外,现实决策问题中权重信息往往难以直接给定[5,6],本文考虑权重信息不完全已知情形,基于直觉模糊余弦相似性测度构建模型求解权重信息。在决策方法上,多准则折衷解排序(VIKOR)法[7]以折衷优化思想为基础,同时考虑最大化群体效益和最小化个体遗憾,得到的排序结果较为稳定,被广泛运用于多属性决策中。

为此,本文针对具有交互作用权重信息不完全已知,且评价值以直觉模糊数形式给出的动态多属性群决策问题,以VIKOR法为基本研究思路,定义广义Shapley直觉模糊Frank-Choquet累积算子,并基于前景理论提出一种直觉模糊加权决策矩阵构造方法,继而提出一种直觉模糊动态多属性群决策方法,最终,通过在“无废城市”建设中应用说明该方法的可行性和有效性。

1 预备知识

1.1 直觉模糊集

定义1[8]设X为一个非空集合,称

A={|x∈X}

(1)

为直觉模糊集,其中μA(x)和vA(x)分别表示X中元素x属于A的隶属度和非隶属度,且满足:μA(x)∈[0,1],vA(x)∈[0,1],0≤μA(x)+vA(x)<1,∀x∈X。另外,称πA(x)=1-μA(x)-vA(x)为X中元素关于集合A的犹豫度。

定义2[3]设α1=(μα1,vα1)和α2=(μα2,vα2)为两个直觉模糊数,λ和γ是两个实数,且λ,γ>0。定义在α1和α2上的Frank加法和数乘运算如下:

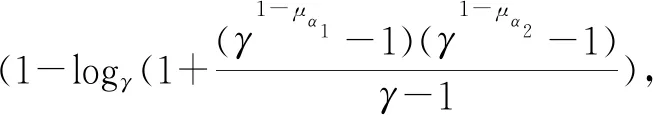
logγ(1+(γvα1-1)(γvα2-1)/(γ-1)))

(2)

λα1=(1-logγ(1+(γ1-μα1-1)λ/(γ-1)λ-1),

logγ(1+(γvα1-1)λ/(γ-1)λ-1))

(3)

定义3[9]设α1=(μα1,vα1)和α2=(μα2,vα2)为两个直觉模糊数,则α1和α2之间的Hamming距离定义如下:

1.2 模糊测度及度量指标

定义4[10]设N={1,2,…,n}是有限集合,定义在N上的模糊测度μ:P(N)→[0,1],满足以下条件:

1)μ(N)=1,μ(Ø)=0;

2)∀A,B∈P(N)并且A⊆B,有μ(A)≤μ(B),其中P(N)是有限集合N上的一个幂集。

定义5[11]令μ为定义在X={x1,x2,x3,…,xn}上一个模糊测度,f为定义在X上的一个非负实值函数,则f关于模糊测度μ的离散Choquet积分定义为:

Cμ(f(x1),f(x2),…,f(xn))

(5)

其中(·)表示定义在X上的一个置换,满足f(x(1))≤f(x(2))≤…≤f(x(n)),A(i)={x(i),x(i+1),…,x(n)},i=1,2,…,n+1,且A(n+1)=Ø。

为更全面反映元素间交互关系,有关学者引入广义Shapley函数[12]如下:

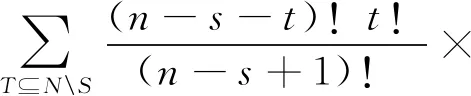
(μ(S∪T)-μ(T)),∀S⊆N

(6)

其中μ是定义在有限集合N={1,2,…,n}上一个模糊测度,n,s和t分别是集合N,S和T中的元素个数。

2 广义Shapley直觉模糊Frank-Choquet累积算子

为反映动态多属性群决策问题中的交互作用,定义广义Shapley直觉模糊Frank-Choquet累积(GS-IFFCA)算子如下所示:

定义6设A={α1,α2,…,αn}为一组直觉模糊数,其中γ>0,则定义在A上的GS-IFFCA算子如下所示:

GS-IFFCA(α1,α2,…,αn)

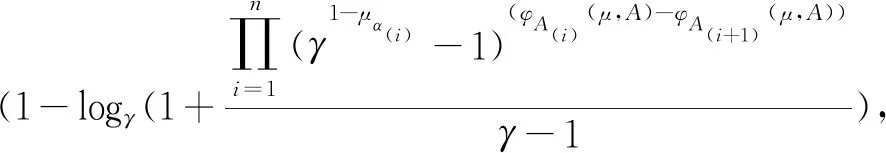
(7)

其中(·)是定义在αi(i=1,2,…,n)上一个置换,满足α(1)≤α(2)≤…≤α(n),且∀i=1,2,…,n有A(i)={α(i),α(i+1),…,α(n)},且A(n+1)=Ø。μ是定义在A(i)上一个模糊测度,φA(i)(μ,α)是集合A(i)关于模糊测度μ的广义Shapley值。

说明:定义6中关于直觉模糊数的排序采用文献13中定义的直觉模糊数分值与准确度函数。

根据上述GS-IFFCA算子定义及直觉模糊Frank加法和数乘运算法则,易证明GS-IFFCA算子具有幂等性、单调性和有界性。此处省略具体证明过程。

3 基于前景理论的直觉模糊加权决策矩阵构造方法

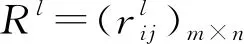
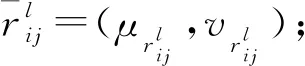
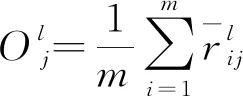
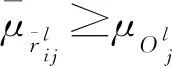
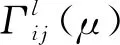
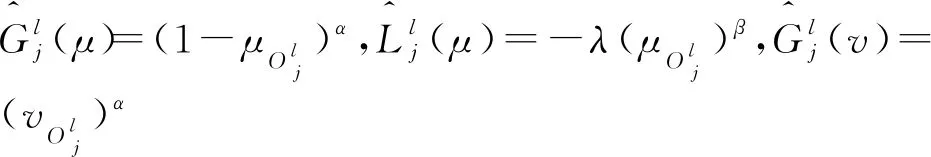
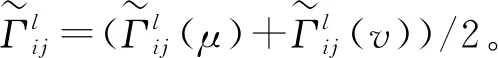
本节提出的直觉模糊加权决策矩阵构造方法既考虑了决策者主观偏好对评价值的影响,又充分考虑直觉模糊特性,同时保证得到的加权决策矩阵仍为直觉模糊矩阵,避免了模糊信息丢失。

4 动态直觉模糊多属性群决策方法

本节首先基于直觉模糊余弦相似性测度建立线性规划模型分别求解专家、时段和属性集上决策权重信息。继而,提出一种动态直觉模糊多属性群决策方法。

4.1 确定权重信息的线性规划模型

定义7[14]设α=(μα,vα)和β=(μβ,vβ)为两个直觉模糊数,则α和β的余弦相似性测度定义如下:

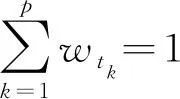
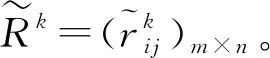
易知,若某时段下评价值和其它时段下评价值越相似,则说明该时段下评价信息越稳定且更具有代表性,应赋予该时段较高权重。令μT为定义在时段集T={t1,t2,…,tp}上模糊测度,建立如下线性规划模型确定模糊测度μT:

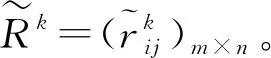
针对属性权重不完全已知情形,令μc为定义在属性集C={c1,c2,…,cn}上模糊测度。建立如下线性规划模型确定模糊测度μc:

4.2 动态直觉模糊多属性群决策方法步骤

本节提出一种动态直觉模糊多属性群决策方法,具体步骤如下所示:

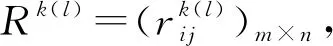
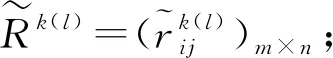
步骤3根据模型(10)建立线性规划模型并求解得各时段下专家权重信息;

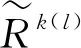
步骤5根据模型(11)建立线性规划模型并求解,得到各时段权重信息;

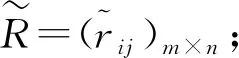
步骤7根据模型(12)建立线性规划模型并求解,得到各属性权重信息;

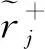
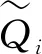
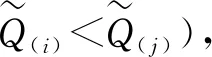
ii)当方案a(1)不满足条件1)时,折衷最优方案为a(1),a(2),…,a(q),其中q为满足Q(q)-Q(1)

步骤10结束。

5 算例分析

“无废城市”建设旨在将固体废物对环境影响降至最低,而一般工业固体废物是整个城市固体废物的重要组成部分,加快推进一般工业固体废物的高质量治理是建设“无废城市”的重要一环。为对“无废城市”建设一般工业固体废物高质量治理方案进行评价,现聘请三位决策专家E={e1,e2,e3}属性集C={c1,c2,…,c6}下对四种方案A={a1,a2,a3,a4}在三个不同时段T={t1,t2,t3}进行评估。

各时段下决策者已知权重信息为:

时段已知权重信息为:

wt1=[0.20,0.30],wt2=[0.25,0.35],wt3=[0.35,0.40]。

属性已知权重信息为:

wc1=[0.15,0.20],wc2=[0.05,0.10],wc3=[0.20,0.25],wc4=[0.10,0.20],wc5=[0.15,0.20],wc6=[0.15,0.20]。

利用本文提出决策方法对上述问题进行求解,得到排序结果为a4≻a3≻a1≻a2,其中各时段下的决策矩阵如表1～3所示。

表1 时段t1下的决策矩阵

表2 时段t2下的决策矩阵

表3 时段t3下的决策矩阵

运用不同决策方法对该问题进行求解,得到排序结果如表4所示。

表4 基于不同决策方法排序结果

从表4可以看出,运用本文方法和先前方法得到的最终排序结果有所不同。这是因为,文献3、15、16中方法均未考虑权重信息不完全已知情形,只是运用不同的直觉模糊算子对决策信息进行融合得到最终方案评价值并排序。方法简单,但未能考虑决策信息间的交互作用,且上述三种方法均未考虑决策者有限理性。本文提出的新方法对上述两方面进行了弥补,具有一定优越性。

6 结论

针对具有交互作用的动态直觉模糊多属性群决策问题,本文首先定义广义Shapley直觉模糊Frank-Choquet累积算子对决策信息进行聚合。考虑决策者有限理性,本文基于前景理论提出一种直觉模糊加权决策矩阵构造方法。为求解未知权重信息,基于直觉模糊余弦相似性测度建立线性规划模型。继而,本文提出一种动态直觉模糊多属性群决策方法,并将该方法运用于“无废城市”一般工业固体废物高质量治理评价问题中,以验证该方法的可行性与有效性。

本文主要创新有:1)提出GS-IFFCA算子用于累积具有交互作用的评价信息;2)基于直觉模糊余弦相似性测度,建立线性规划模型确定决策权重信息;3)基于前景理论提出直觉模糊加权决策矩阵构造方法。本文提出的新方法还可运用于医疗诊断、选址评价、投资决策等复杂动态决策问题。