基于GA-PSO 混合优化BP 的面板堆石坝爆破料压实质量评价
宿 辉,孙熇远,赵宇飞,刘世伟,赵翠东,杨 宇
(1.河北省智慧水利重点实验室,河北 邯郸 056006;2.河北工程大学 水利水电学院,河北 邯郸 056006;3.中国水利水电科学研究院,北京 100044)
随着智慧水利的长足发展,大坝施工逐渐由传统施工模式向数字化、信息化和自动化转变[1]。土石坝压实质量评价是实现水利工程大坝智能化施工的关键,这不仅关系到大坝安全稳定,而且可为现场施工和大坝安全管理提供支持[2]。传统评价方法通常采用试坑采样或快速检测(如落锤弯沉计、核子密度计等)获取干密度(孔隙率)。但这些方法均为事后抽样检测,存在随机性和滞后性,且不能反映施工等因素影响[3]。然而,坝体填筑料在碾压机械的重力和振动作用下,颗粒间产生相对移动,孔隙减小,坝料被压实,石料间嵌锁的紧密程度越高压实结果越好[4]。可见,土石坝压实质量受料源参数和碾压参数的双重影响,因此关于多因素影响下的大坝碾压质量实时有效评价亟待开展进一步深入研究。
事实上,国内外学者已对多因素影响下的大坝碾压质量实时有效评价开展了诸多研究并取得了丰硕成果。例如,刘东海等[5-6]分析了碾压参数(碾压速度、碾压厚度、碾压遍数等)和料源参数与土石坝压实监测指标的相关性;Anderegg 等[7]通过智能碾压系统,研究了不同级配比土料与压实监测指标FS 的相关性;Mooney 等[8]通过分析压路机在压实中的振动变化规律,发现了振动频率和振动幅度同样影响压实质量。刘东海等[9-10]基于碾压实时监控系统获得的碾压参数数据,建立了多元回归模型和人工神经网络模型,预测压实质量;王晓玲等[11]依托大坝碾压实时监控系统,考虑碾压遍数、碾压速度和不均匀系数等参数,通过遗传算法优化的BP 神经网络和可靠度理论建立了土石坝堆石料干密度-可靠度二元耦合模型,实现了压实质量全面评价;王佳俊等[12-13]考虑不同类型的数据,基于混沌萤火虫算法(CFA)、增强概率神经网络和支持向量回归算法(SVR),实现了仓面的压实质量全面评价,提高了模型的预测精度;林威伟等[14]基于随机森林算法,考虑料源参数的不确定性,建立土石坝压实质量评价模型,并通过Kriging 插值方法进行全仓面压实质量动态评价;崔博等[15]基于双向极限学习机算法,在先前研究的基础上考虑施工全过程参数,建立了掺砾土心墙压实质量实时评价模型。
上述研究不仅厘清了料源参数(含水率、P5 含量、不均匀系数等)和碾压参数(碾压速度、碾压厚度、激振频率、碾压遍数等)是影响土石坝压实质量的主控因素,建立了可以表征干密度、相对密度和孔隙率等压实质量的评价指标,还提出了多元线性模型、支持向量回归模型、极限学习机模型和神经网络预测模型等常用的压实质量评价模型。但是现有研究成果在高面板堆石坝研究中应用较少,且诸多评价模型各有优缺点,其合理选择和适用性尚未形成一致意见。
鉴于以上所述,在现有研究成果的基础上,本文选取碾压参数(碾压遍数、碾压速度、碾压厚度、激振频率)和料源参数(P5 含量、最大粒径、平均含水率)建立影响因子集,构建基于GA-PSO-BP 神经网络的面板堆石坝爆破料压实质量评价模型,结合新疆阿尔塔什面板堆石坝的碾压施工现场实测数据,开展坝体碾压质量评价与预测。相关研究成果有望为土石坝碾压施工管理提供理论支持。
1 基于GA-PSO-BP 的面板堆石坝爆破料压实质量评价方法
1.1 大坝压实质量评价模型结构
大坝压实质量评价模型结构主要包括评价指标量化表征和大坝压实质量概念化评价模型两部分内容。
1.1.1 评价指标量化表征
影响大坝压实质量的主控因素可分为料源参数和碾压参数。本文选取的料源参数因子集MSP包含料源P5 含量HP5、最大粒径Mmax、平均含水率W3 个因子;碾压参数因子集RP包含碾压遍数N、碾压速度V(指碾压机械的行车速度)、碾压厚度h、激振频率f四个因子。同时,压实质量评价指标采用孔隙率n或压实度K,并依据《混凝土面板堆石坝施工规范》(SL 49—2015)[16]取值,且选取孔隙率n为评价输出指标。
式(1)中,碾压参数因子集数据源于土石坝碾压监控系统,料源参数因子集数据源于现场施工检测,孔隙率由碾压完成后的试坑抽样检测获取。
1.1.2 大坝压实质量概念化评价模型
以孔隙率n为输出结果,以料源参数因子集MSP和碾压参数因子集RP为输入,建立大坝压实质量评价目标函数如下:
采用智能优化算法对上述目标函数进行计算求解,本文拟采用GA-PSO 混合优化后的BP 神经网络进行求解。构建基于GA-PSO-BP 的算法孔隙率评价预测模型如下:
式中:x、q、y分别为BP 神经网络输入层、隐含层、输出层的神经元个数;v、w分别为输入层与隐含层连接权值、隐含层与输出层的连接权值;θ、γ分别为输出层、隐含层的阈值。上述参数可通过以料源参数因子集MSP和碾压参数因子集RP组成的数据集database确定。而预测精度评价test部分,主要与基于BP 算法的预测模型ABP、基于GA-BP 算法的预测模型BGA-BP和基于PSO-BP算法的预测模型CPSO-BP3 种模型预测结果进行对比分析,以决定系数R2、平均相对误差MRE和均方根误差RMSE为模型预测精度的3 个评价指标。
1.2 基于GA-PSO 混合优化后的BP 神经网络算法
BP 神经网络是一种按误差反向传播训练的多层前馈网络。基本BP 算法包括信号的前向传播和误差的反向传播两个过程,一般由输入层、隐含层和输出层组成(见图1)。从理论上讲,一个3 层的BP 神经网络就能够在保证精度的情况下实现对任意连续函数的逼近,但是BP 神经网络计算容易陷入局部最优,导致模型训练失败[17]。

图1 爆破料孔隙率BP 神经网络结构
1.2.1 GA 算法
GA(遗传)算法是一种基于生物进化理论和基因遗传原理而提出来的一种智能优化算法。其通过设计一定数量种群在特定环境中生存,利用选择、交叉和变异3 种操作去模拟适者生存和优胜劣汰原理来获得最优个体,从而得到问题的最优解。选择、交叉和变异作为遗传算法的核心操作,其过程如下。
(1)选择。通过选择操作实现种群的淘汰与保留,最常用轮盘赌选择法,其中fi为个体i的适应度值,每个个体被选择保留的概率为
(2)交叉。将选择留下的优秀个体进行随机搭配,以一定的概率将选择个体的部分染色体进行交换,交叉操作为
式中:r1为在0~1 范围内的随机数;Si c、Szc分别为第i、第z个染色体在第c位上的交叉操作。
(3)变异。通过个体以一定概率进行变异,能够增加种群的多样性、提高遗传算法的全局搜索能力,其具体计算如下:
1.2.2 PSO 算法
PSO(粒子群)算法源于对鸟群捕食的行为研究,通过群体中个体之间的协作和信息共享来寻找最优解具有良好的全局搜索能力,属于全局优化算法。设该种群有N个粒子,粒子的速度和位置更新公式为
1.2.3 GA-PSO 混合优化算法
PSO 算法在寻优过程中采用并行随机搜索的方法,通过该方法能够以极快速度精准接近目标,但寻优过程中易陷入局部极值出现“早熟”现象[18];GA 算法则基于优胜劣汰原理,在计算过程中种群不断淘汰更新,导致信息丢失、算法收敛速度较慢[19]。因此,针对PSO 算法收敛快但易陷入局部最优和GA 算法收敛慢但全局搜索能力强的特点,本文提出GA-PSO 混合优化算法。以PSO 算法为主体,通过将GA 算法中的选择、交叉、变异等操作引入其中,使得新算法(GA-PSO混合优化算法)具有GA 算法的全局搜索能力和PSO算法收敛速度快等优点。
GA-PSO 混合优化算法基本思路为:与原有PSO算法不同,在PSO 算法每次迭代寻优时,种群会被平均分为两份,适应度值小的种群命名P1,适应度值大的种群为P2;种群P1中粒子由于适应度小,其位置信息、速度和适应度不变,对于种群P2中的粒子进行位置更新的同时引入变异,速度更新时引入交叉操作;通过变异交叉后的种群P2、P1进行适应度值大小比较,选择适应度值最小粒子所处位置和搜索速度并对当前种群进行更新。
1.2.4 基于GA-PSO 混合优化后的BP 神经网络算法(GA-PSO-BP)
为了弥补BP 神经网络算法全局搜索能力较差的不足,本文利用GA-PSO 混合算法的全局搜索能力强和快速收敛等优点获取BP 神经网络的全局最优初始权值和阈值,建立基于粒子群算法优化的BP 神经网络模型,进而结合大坝压实质量影响因子集构建其压实质量评价模型。
(1)建立一个3 层结构的BP 神经网络,初始化粒子群的速度与位置等参数。
(2)计算所有粒子的适应度,通过适应度函数值来确定各个粒子是否处在合适位置。本文选择BP 神经网络的误差函数E(ω)作为适应度函数:
式中:L为输入样本的总数;Yi、Zi分别第i个粒子的预测输出、实际结果。适应度函数值越小,说明模型拟合结果越好。
(3)引入遗传算法中的选择操作。将各个粒子按适应度值从小到大排列并将种群平分为P1和P2,将二者适应度值进行比较,选择适应度值较大的种群P2进行遗传算法中的交叉和变异,同时种群P1中适应度值、速度和位置不变。通过该方法,能保留更多的优秀粒子且获得更小的适应度值,从而加快算法的收敛速度。
(4)在种群P2中粒子进行速度更新时,引入GA算法中的交叉操作,新的速度更新公式为
(5)在种群P2中粒子进行位置信息更新时,引入GA 算法中的变异操作,新的位置更新公式为
式中:X上、X下分别为当前粒子位置的上、下边界值;r3、r4为0~1 范围内的随机数;k为迭代次数;f(k)为变异概率。基于变异操作可使粒子跳出局部最优解。
(6)对经过交叉、变异操作的新种群P2、P1比较适应度值,并更新位置和速度。
(7)判定算法是否达到终止条件,即达到最大迭代进化次数或设定最小适应度值。若达到要求,则进行步骤(8),否则返回步骤(2)重复迭代。
(8)将GA-PSO 混合优化算法计算得到的最优初始权值和阈值赋予BP 神经网络作为神经网络参数。
GA-PSO 混合优化BP 神经网络的流程见图2。

图2 基于GA-PSO 混合优化BP 流程
1.3 基于GA-PSO-BP 算法的压实质量评价模型
(1)数据层。通过现场获取的料源参数因子集MSP、碾压参数因子集RP、孔隙率n等数据,基于时空关联性对3 种数据进行时间和空间上的配对,构建原始数据集[20]。对评价数据集进行数据优化、标准化和归一化处理,对异常数据等进行剔除。标准化和归一化能够提高网络的训练速度和预测精度,消除量纲差异的影响。
(2)模型层。以P5 含量、平均含水率、最大粒径、碾压速度、碾压遍数、碾压厚度、激振频率作为输入神经元,以孔隙率n为输出神经元,基于PSO-BP 神经网络,构建坝体填筑料压实质量评价模型。
(3)模型训练。采用GA-PSO-BP 算法,以输入神经元为输入参数,以输出神经元为输出结果,数据集以7 ∶3 分为训练集和测试集,完成模型构建,形成基于GA-PSO-BP 算法的压实质量评价模型。
(4)对比验证。以测试集数据为研究对象,选用不同评价指标(决定系数R2、均方根误差RMSE、平均绝对误差MRE)对模型在测试集上的预测结果进行精度评价,并与BP、GA-BP、PSO-BP 三种模型预测结果进行对比分析,验证本文模型的有效性与准确性。
2 工程应用与验证
2.1 工程概况
新疆阿尔塔什水利枢纽位于新疆喀什地区莎车县,该工程为大(1)型Ⅰ等工程,电站总装机容量755 MW,多年平均年发电量21.86 亿kW·h,最大坝高164.8 m。该工程拦河大坝为混凝土面板堆石坝,下游次堆石区填料为爆破料,其起到保护主堆石区及下游边坡稳定的作用,下游次堆石区的填筑碾压质量极大影响大坝的安全,爆破料特征粒径见表1。本文结合下游次堆石区现场碾压数据进行土石坝压实质量评价模型研究,根据新疆阿尔塔什面板堆石坝碾压监控系统、工程现场检测数据和抽样试坑检测试验结果,通过统计核算后共106 组有效数据作为本次研究数据。

表1 爆破料特征粒径 mm
2.2 参数相关性分析
本次工程评价根据施工规范选取孔隙率作为输出参数,孔隙率作为压实质量评价指标受诸多因素的影响,如碾压参数和料源参数等。对于新疆阿尔塔什混凝土面板堆石坝下游次堆石区爆破料工况条件而言,P5 含量是控制填料良好级配的重要指标;考虑到爆破料粒径较大且在阿尔塔什工程级配控制中要求最大粒径小于500 mm,水分能够使填料软化润滑、有利于压实,因此在料源参数选取上本文选择P5 含量、最大粒径和平均含水率,同时碾压参数作为碾压施工过程中的主要控制参数,其与压实质量的相关性已被诸多文献证明[10-13]。为保证所建立数据集对阿尔塔什面板堆石坝的适用性,本文利用Pearson 相关系数,对阿尔塔什面板堆石坝爆破料孔隙率与各影响因子的相关性作进一步分析。Pearson 相关系数可以表示变量之间的相关性,其值介于-1.0 与1.0 之间、绝对值越接近1.0,说明变量之间的相关性越高[21]。
新疆阿尔塔什混凝土面板堆石坝下游次堆石区填料压实后的孔隙率指标与碾压参数和料源参数的相关性分析结果见图3。由图3 可知:碾压厚度与孔隙率的相关系数绝对值最大,为0.808,说明二者存在明显的负相关;P5 含量、最大粒径、平均含水率、碾压遍数和激振频率与孔隙率的相关系数绝对值均在0.5 以上,具有较高的相关性;碾压速度与含水率的相关系数为0.366,虽然二者相关系数相对较小,但是碾压速度对填筑料压实质量具有重要影响,并得到诸多学者一致认可[1,6,11,14-15]。因此,为了保证本文模型预测结果的可靠性,选取平均含水率、最大粒径、P5 含量、碾压速度、碾压厚度、激振频率和碾压遍数作为模型的输入参数,孔隙率作为模型的输出参数。
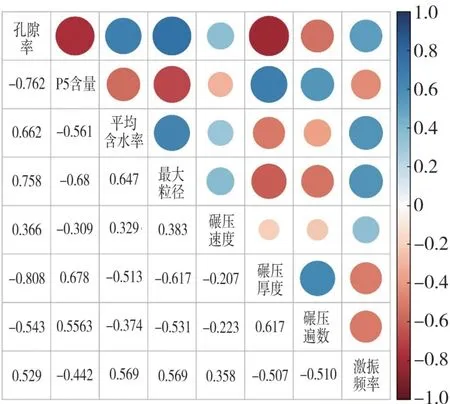
图3 模型输入参数与孔隙率相关系数矩阵
2.3 预测结果与性能评价
经过多次训练测试,模型参数设置如下:构建一个7-12-1 三层的BP 神经网络,本文BP 神经网络的隐含层、输出层激励函数分别为Tansig 函数、Logsig 函数;种群数为20,最大迭代次数为100,学习因子c1、c2均为1.4,交叉概率为0.7,变异概率为0.01,惯性权重系数ωmax、ωmin分别为0.9、0.4,粒子搜索速度范围为-3~3。GA-PSO-BP、GA-BP、PSO-BP 评价模型的收敛变化曲线见图4,在相同的模型参数设置下,经过100 次的进化迭代,GA-PSO-BP 评价模型具有更好的收敛速度和求解精度,能够保证以较快的收敛速度达到更优的适应度,提高了BP 神经网络的收敛速度。

图4 GA-PSO-BP 与其他评价模型收敛变化曲线
4 种压实质量评价模型孔隙率预测结果与现场实测结果对比见图5。以R2、MRE、RMSE作为4 种模型的预测精度评价指标,模型预测精度对比分析见表2、图6。通过与BP、GA-BP、PSO-BP 3 种评价模型进行对比分析发现,本文模型预测结果与实测结果的相符程度高、误差小,表明本文提出的基于GA-PSO 混合优化的BP 神经网络评价模型具有优越性。

表2 4 种模型训练集和测试集性能评价指标对比

图5 孔隙率预测结果和实测结果对比

图6 4 种模型预测误差对比曲线
由图5 可知,GA-PSO-BP 模型的拟合效果最好,另外3 种模型均在孔隙率数值波动较大处出现拟合效果较差的情况,可见本文提出的GA-PSO-BP 模型预测精度相对较高。由表2 可知,GA-PSO-BP 模型测试集的决定系数R2为0.83,与训练集相差较小,而其他3 种模型测试集和训练集的决定系数相差较大且均出现了轻微的过拟合现象,表明本文模型的泛化性能更为优越;平均相对误差和均方根误差反映了模型的预测精度,其值越小说明精度越高,本文模型测试集的平均绝对误差、均方根误差分别0.002 5、0.003 7,均为4 种模型中的最小值,表明GA-PSO-BP 评价模型能够更好地逼近实测值。
由图6 可知,GA-PSO-BP 模型预测误差波动范围大都为[-0.005,0.005],而其他3 种模型预测误差波动范围为[-0.01,0.01],说明GA-PSO-BP 模型更为稳定、泛化性能更优。
综上可见,本文提出的基于GA-PSO-BP 算法的压实质量评价模型对于新疆阿尔塔什面板堆石坝下游次堆石区爆破料压实后的孔隙率预测精度和泛化性能均较好,可应用于类似工况条件下坝体填料压实质量的评价。
3 结论
(1)通过参数相关性分析表明,对于新疆阿尔塔什混凝土面板堆石坝下游次堆石区爆破料碾压施工而言,压实后填料的孔隙率与碾压速度、碾压遍数、碾压厚度、激振频率、平均含水率、最大粒径、P5 含量7 个指标具有良好的相关性,可作为新疆阿尔塔什混凝土面板堆石坝下游次堆石区爆破料压实质量的评价因子。
(2)本文提出了基于GA-PSO-BP 算法的爆破料压实质量评价模型。首先,将GA 算法的全局搜索能力与PSO 算法的快速收敛能力相融合,提高了算法的局部搜索能力和收敛速度;然后,结合现场实测数据,与BP、GA-BP、PSO-BP 三种模型进行对比分析,验证GA-PSO-BP 模型的可靠性和精确度。结果表明,基于GA-PSO-BP 算法的爆破料压实质量评价模型能够用于该工程压实质量评价,相关研究成果可为土石坝智能施工管理提供参考。

