40m预应力混凝土T梁静载破坏试验研究

侯敏

（中国铁建股份有限公司，北京 100855）

1 工程概况

某4×40m 简支变连续梁桥，共14 联，平面处于一条直线上，双向六车道，设计时速120km，公路-Ⅰ级荷载。上部采用先简支后连续预应力混凝土T 梁，C50混凝土，部分预应力A 类构件。横断面如图1 所示。

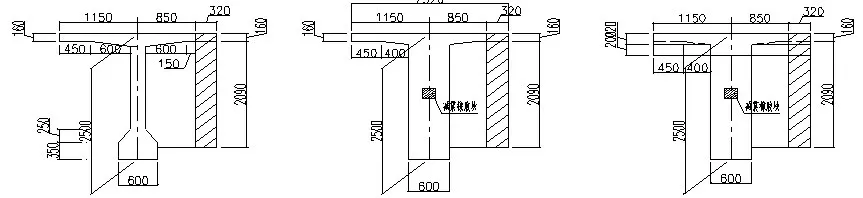
图1 T 梁横断面图（单位：mm）

图2 竖向位移观测点位排布

2 T 梁破坏试验

2.1 试验目的和主要内容

2.1.1 主要目的

（1）通过静载试验，观察、测试T 梁的工作状态并记录试验数据，分析该梁体工作状况是否符合设计有关要求；

（2）实测T 梁的消压以及开裂弯矩，并与理论值进行比较；

（3）在试验荷载作用下，对梁体裂缝产生及发展情况进行观测，分析裂缝性质及发展规律；

（4）借助试验结果，对试验对象承载力及工作状态进行综合性评价。

2.1.2 主要内容

（1）资料收集、试验分析

收集相关设计施工资料，对试验梁进行理论计算和分析。包括：梁片的应力计算、加载重量等级的确定、测试数据处理和分析。

（2）现场测试和数据分析处理

步骤一：采用千斤顶反力梁装置，在现场逐级加载，并及时记录每级荷载应变数据，当跨中底部出现竖向裂缝时即停加载，记录此时荷载值，并计算对应开裂弯矩；然后缓慢卸载，当裂缝消失时再次记录试验数据，计算跨中消压弯矩。

步骤二：卸载后，重复步骤一两遍。

步骤三：当卸载完成，继续逐级加载，直至跨中底部出现10mm 宽裂缝时停止加载，记录荷载数据，之后完成卸载。

通过上述方法，观测试验梁选定截面（见图3）在各级荷载作用下的应力、变形及裂缝发展状况，主要包括：

图3 b-b、c-c、d-d 截面应变测点布置(单位：mm)

图4 应变测点布置图（a-a 断面、e-e 断面有横隔板侧）（单位：mm）

图5 有横隔板侧应变测点及编号示意

①aa、ee 截面：最大剪应力、支座沉降；

②bb、cc、dd 截面：顶板、底板、腹板的混凝土应变及挠度变化；

③裂缝观察测量：是否存在既有裂缝以及新裂缝发展情况。

2.2 采用方法

2.2.1 测点布置

参照桥梁试验相关规范，通过对设计文件和相关资料的分析，选取5 个试验截面，并确定测点位置，测点布设如图2～图6 所示。

图6 无横隔板侧应变测点及编号示意（单位:mm）

2.2.2 加载原则

（1）试验加载按逐级加载方式进行，并准确测出开裂弯矩以及消压弯矩，得出截面应力应变、挠度随试验荷载的变化关系。

（2）试验应该选择在温度变化较小的时段进行，旨在消除温差对试验结果的影响。

2.2.3 试验荷载的确定

计算试验梁的理论消压和开裂弯矩，并根据理论结果选取逐级加载重量。

（1）加载位置如图7 所示。

图7 加载位置图

加载重量按公式（1）计算：

式（1）中：M 为理论弯矩；L 为计算跨径；a 为两个加载点之间的距离。

（2）理论计算

（a）考虑荷载横向分布进行计算：

一是由专业软件计算出边梁荷载横向分布系数m=0.58。

二是根据《公路桥涵设计通用规范》（JTG D60—2015），取l=38.65m,E=34.5×109Pa,Ic=0.87m4,A=1.16m2(梁跨中截面断面积),mc=1.16×1×2.6×103=3.02×103kg/m，则：

由于1.5Hz ≤f1≤14Hz,可得冲击系数μ=0.1767lnf1-0.0157=0.2。

三是取多车道折减系数ζ 为0.78，则传递到边梁的均布荷载：

传递到边梁的集中荷载：

以上集中荷载和均布荷载共同作用下跨中最大弯矩值：

外荷载作用下等效理论加载重量：

（b）根据截面计算

一是梁跨中截面底部应力为零时理论加载重量计算：

消压弯矩计算：

通过力的平衡，可算出σmax=12.623MPa，M消压=15479.3kN·m；

自重作用下产生的弯矩计算：

由自重产生的跨中弯矩为M自重=29×38.652/8=5415.1kN·m；

外力产生的弯矩 M外=M消压-M自重=10064.2kN·m；

则理论加载重量P=785.7kN。

二是梁跨中截面底端开裂时理论加载重量计算：

抗裂弯矩Mcr'=γftkW0，

γ 为截面抵抗矩塑形影响系数，γ=（0.7+120/1600）×1.5=1.16，

ftk取2.64MPa，W0=0.607596m3，

则抗裂弯矩为Mcr'=1864.7kN·m，对应的试验加载重量为145.4kN，

故梁下缘开裂时总试验加载重量P=785.7+145.4=931.1kN。

（c）有限元软件建模计算

试验梁采用Midas 软件建模，模型分52 个单元，53 个节点，如图8 所示。

图8 Midas 模型

在试验梁建模过程中，通过计算对比发现，普通钢筋对梁消压和开裂弯矩影响可忽略，基于此可得：

跨中截面底端压应力为零时，对应消压弯矩为9450kN·m，支座截面产生的剪力为700kN。

跨中截面底端出现裂缝时，对应开裂弯矩为12825kN·m，支座截面产生的剪力为950kN。

（3）选取逐级加载重量

据以上计算，消压弯矩加载重量为700kN，开裂弯矩加载重量为950kN，试验过程共分7 个等级逐级加载，1～7 级加载重量P 分别为188kN、344kN、450kN、650kN、850kN、1050kN、1200kN。

2.3 试验数据

2.3.1 应力测试

按前述试验步骤进行荷载试验，并对试验数据进行统计处理，如表1、表2 和图9、图10 所示。

表2 1/4 截面应力实测数据

图9 跨中截面应力实测数据折线

图10 1/4 截面应力实测数据折线

根据试验数据，绘制T 梁在各级加载重量下，主要控制截面的应力分布情况图，得出结论：一是梁体在开裂之前，其主要控制截面上的应力分布基本随截面高度呈线性变化，符合平截面假定；二是在最大加载重量下，T 梁截面承受的拉、压应力最大，跨中截面产生的最大压应力为-9.3MPa、最大拉应力为16.5MPa，1/4 截面产生的最大压应力为-8.19MPa、最大拉应力为21.73MPa。

2.3.2 挠度测试

逐级缓慢加载，根据仪表测得梁底挠度，绘制该梁跨中截面在荷载不同等级作用下的荷载—挠度曲线图，如表3、图11 所示。

表3 跨中荷载挠度值

图11 跨中荷载—挠度曲线

通过以上试验，分析得出：一是在梁体开裂前，随着各级荷载增加，跨中截面挠度随荷载弯矩基本呈线性变化，与结构计算理论相符，说明该梁体在弹性范围工作；二是当试验弯矩达到4644kN·m(大于设计荷载弯矩3810kN·m)时，跨中最大挠度实测8.15mm，对应挠跨比1/4900，满足相关规范对刚度1/600 的限值要求。

2.3.3 裂缝观测

经观测：在试验荷载P 加载到约110t 时，梁体跨中附近底部开始产生竖向裂缝，且随着试验荷载的逐渐增加，既有裂缝不断向上发展，同时从跨中附近向支座方向对称出现新竖向裂缝；当P 达到120t 时，裂缝已经从梁体底部发展到腹板；第一次加载完毕后，在逐渐卸载过程中，当P=70t 时，裂缝闭合；第二次加载到P=70t 时，梁体跨中附近截面底端即出现裂缝。

3 结论

第一，试验梁的消压弯矩为9450kN·m，此时试验荷载P=700kN；

第二，试验梁的开裂弯矩为14850kN·m，此时试验荷载P=1100kN；

第三，在设计荷载下跨中挠度小于8.15mm，对应挠跨比小于1/4900，满足设计指标要求（1/600）；

第四，实测的消压弯矩与理论值吻合度高见表4，该值相比设计承载力，有较大的安全储备，说明梁具有足够的安全性；

表4 理论计算和实测对比数据

第五，裂缝发生及开展的均匀性说明梁的普通钢筋配置较合理。