A3C 深度强化学习模型压缩及知识抽取
张 晶 王子铭 任永功
(辽宁师范大学计算机与人工智能学院 辽宁 大连 116081)
强化学习(reinforcement learning,RL)作为人工智能的重要研究方向,在路径规划[1]、生产自动化[2]、辅助驾驶[3]等领域被广泛应用.不同于经典监督或无监督机器学习模型,强化学习构建智能体与未知环境逐步交互获取时序相关状态数据,并根据当前时刻状态选择动作,求解不同目标下最优化行为策略及最大累积反馈,使智能体通过对环境连续自由探索强化自主学习能力[4-6].
经典强化学习方法基于动态规划理论,在已知环境模型中更新智能体策略,获得最优化累积反馈.然而,该类方法在求解过程中需借助状态转移概率,为自由环境建模带来了困难.基于统计理论的蒙特卡罗思想为解决上述问题提供了有效途径,其利用大量随机采样的状态-动作时序序列统计均值作为状态值函数的无偏估计建模.同时,研究者进一步拓展、增量蒙特卡罗理论,提出时序差分(temporal difference,TD)的强化学习模型,在避免采样量过大等问题的同时实现对连续、无限环境状态空间学习.基于TD 理论的强化学习方法受到学者广泛关注,Watkins[7]提出Q 学习算法(Q-Learning),借助表格保存策略,并利用异策略的方式对动作值函数更新建模,但该方法在复杂场景中存在采样低效的问题.针对该问题,Sutton[8]提出基于模型的强化学习框架Dyna-Q 模型,通过对环境产生的仿真经验辅助策略更新.然而,其仍然无法解决智能体对高维连续图像环境的探索问题.
深度卷积网络的发展,为智能体高维连续图像环境探索问题的解决提供了有力条件[9-10],同时,有研究者提出的深度强化学习模型,将强化学习在工业领域中的表现推向了新的高度[11-18].基于值函数近似方法的深度强化学习模型利用智能体对接收环境的状态估值,选取状态下最优动作的方式对策略间接求解,其由深度Q 网络(deep Q-network,DQN)[4,18-20]发展而来.为解决环境中存在的部分可观测问题.Kapturowski 等人[21]拓展原始DQN 模型,提出利用循环神经网络(recurrent replay distributed DQN,R2D2)构建智能体,并提出从经验池中部分采样训练初始网络后利用剩余样本更新网络参数,一定程度上缓解表征偏差和滞后问题.针对强化学习中常见的连续动作空间问题[6,22].Sutton 等人[23]同时利用深度网络结构构建动作值函数及实现策略求解,提出演员评论家(actor-critic,AC)算法.该方法基于深度神经网络学习模型,针对连续动作空间,构建策略网络与价值网络,利用策略网络与环境交互,价值网络对结果评价的过程,实现策略直接求解,并结合策略梯度(policy gradient,PG)[24]与TD,解决因反馈值方差过大而无法收敛的问题.
然而,大规模深度强化学习模型训练速度慢、学习时间长等问题导致模型面对高实时性要求的问题时失效[25].基于此,分布式深度强化学习算法利用丰富的并行计算资源,将智能体大量复制,并与环境交互,实现在单位时间内快速积累经验信息,达到数倍于传统深度强化学习模型的学习效率,高效解决复杂环境学习与探索问题[26].Nair 和Li 等人[27-28]提出参数服务器框架,通过对学习者(learner)进行参数及梯度同步,获得通用并行强化学习架构(general parallel reinforcement learning architecture,Gorila),实现多智能体并行探索.为进一步扩大并行规模,提升环境采样效率与模型训练数据吞吐量,Horgan 和Schanl[29-30]引入优先经验回放(priority experience replay)机制,进一步提出并行分布式优先经验回放(distributed priority experience replay,Ape-X)模型.Mnih 等人[25]基于AC结构基础上提出异步优势演员评论家(asynchronous advantage actor-critic,A3C)框架,建立多个AC 架构下的智能体与环境交互,利用异步并行的方式更新网络参数.OpenAI 为解决A3C 并行框架中无法有效使用异构计算资源,例如,GPU 问题,提出智能体同步并行的同步优势演员评论家(synchronous advantage actor-critic,A2C)框架,该算法无需使用经验池(replay memory),并对连续动作空间有更好的支持[31].然而,相比于A2C,A3C 的异步并行训练方式无需在每轮参数更新时等待所有并行智能体采样完成,同时,也没有完成异构计算中的数据通信开销,在训练规模较大且智能体策略并不十分复杂的情况下A3C 算法十分有效且高效.然而深度强化学习采样过程中产生的高方差学习特点,带来了2 个重要问题:
1)全局模型非最优模型.A3C 在训练终止时,留存在各个进程上并行计算的子智能体将保留独立且互不相同的学习模型,测试阶段主智能体使用某一子智能体作为全局模型,该过程受深度学习高方差解影响,难以保证全局最优性[32],如图1 所示,A3C 并行框架执行在经典Atari 的Breakout 环境中,主智能体Learner 最终更新参数非全局最优,此时学习反馈曲线呈现下降趋势,导致环境中智能体执行效果不理想.根据图1,环境中最优子智能体Worker_2 反馈
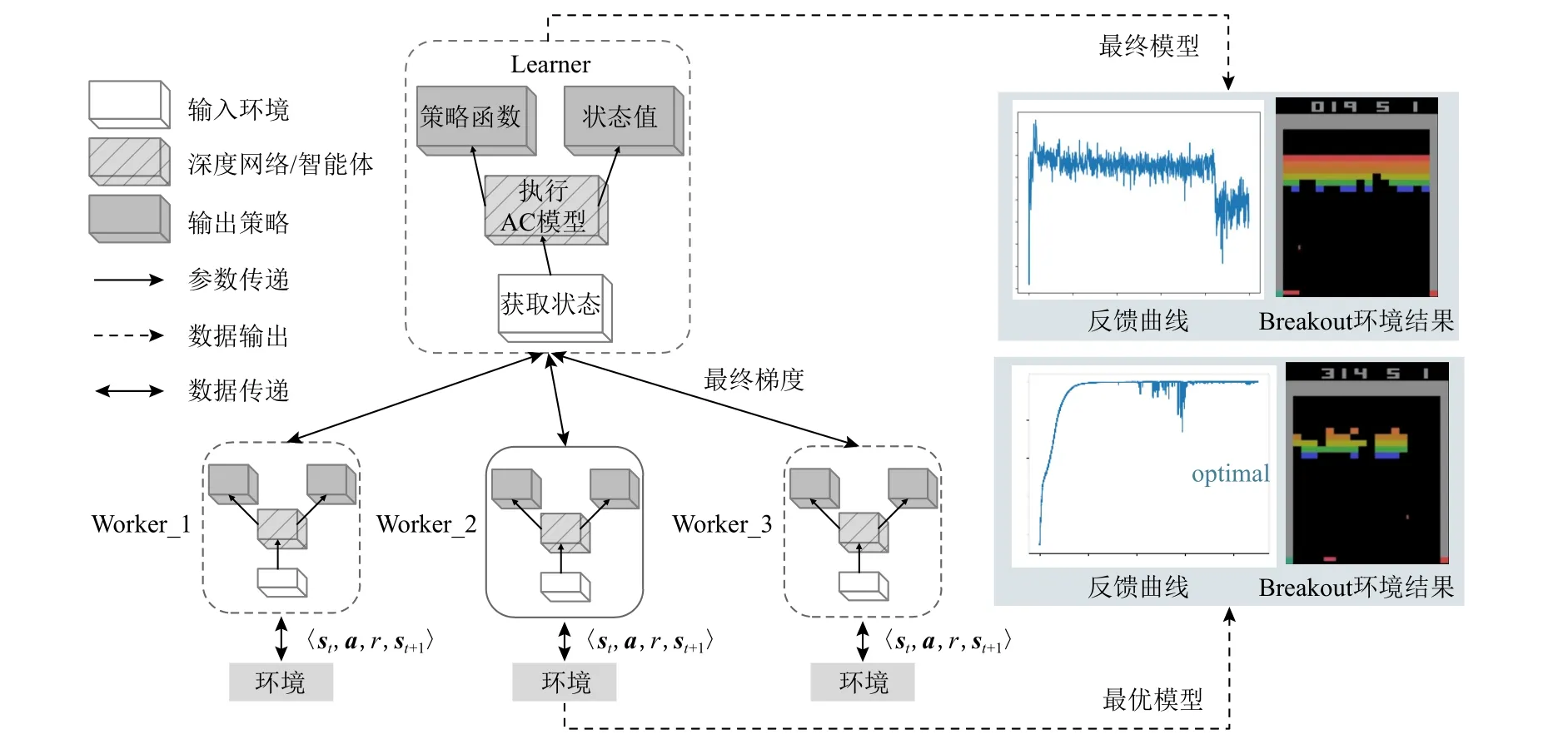
Fig.1 The updated process of non-global optimum parameters in A3C learning图1 A3C 学习中非全局最优参数更新过程
曲线呈现上升、平稳状态,利用该子智能体更新主智能体Learner 后在环境中取得了更好效果.
2)难以近端迁移且并行计算资源浪费.低效的经验数据利用率,使A3C 常需要百万计与环境交互的次数和巨大的算力资源,可在较为复杂环境中达到一定测试精度.同时,该种并行网络规模难以迁移到移动平台或低功耗近端平台部署[33].针对此问题,Hester 等人[34]提出利用专家策略产生的经验数据使智能体进行快速学习,但该方法应用范围仅限于过程策略算法off-policy[35-36].Rusu 等人[37]受Hinton 等人[38]在监督学习网络压缩过程中提出网络蒸馏概念的启发,提出针对强化学习的策略蒸馏 (policy distillation)模型,其利用大规模强化学习模型指导较小规模模型,完成现有策略模型间的迁移.然而,该方法仅通过分布度量近似的方式实现网络压缩,未考虑A3C 框架中模型异步更新学习方式,难以直接迁移和实现知识抽取及模型压缩.
针对全局模型非最优模型及大模型难以近端迁移的问题,本文提出A3C 深度强化学习模型压缩框架Compact_A3C,该框架依概率将原始A3C 中经逐次迭代训练后,贡献更大的子智能体激活,并将参数快速迁移到主智能体,构建用于知识抽取及模型压缩的最优“教师网络”.同时,利用“教师网络”监督小规模“学生网络”前期探索学习,并通过损失函数线性衰减鼓励“学生网络”智能体自由探索,提升最优解学习精度与速度.本文所提出算法主要有3 点贡献:
1)提出异步并行深度强化模型A3C 的网络压缩框架Compact_A3C,解决子智能体高方差学习问题,实现最优知识抽取;鼓励并行框架广泛探索,使大规模A3C 模型近端迁移成为可能,并为其他大规模并行强化模型的网络压缩及知识抽取方法提供新思路.
2)Compact_A3C 通过自动激活,选取全局最优化子智能体构建“教师网络”.利用大规模并行强化模型对环境充分探索,积累学习经验,避免资源浪费;同时,通过最优“教师网络”监督小规模“学生网络”实现早期环境探索及学习,显著减少“学生网络”与环境交互次数,实现最优策略指导;并利用线性衰减影响,鼓励智能体自由探索,强化学习能力,完成模型压缩与知识抽取.
3)利用Compact_A3 获得小规模“学生网络”,其参数量仅为“教师网络”参数规模20%~45%,在目前流行的Atari 2600 与Gym Classic Control[37,39-40]实验环境中依然可达到与A3C 大规模并行网络一致的学习性能.
1 相关工作
1.1 演员-评论家模型
强化学习基于有限马尔可夫决策过程(Markov decision process, MDP),通过构建智能体与环境交互实现具体目标.智能体每一时刻t=0,1,2,…,T在环境中探索,获取环境状态特征表达st∈S,凭借探索策略π ∈[0,1],选取最优化动作at∈A(st),得到动作反馈rt+1∈R⊂R,并获取下一时刻环境状态st+1.该过程构建状态、动作、反馈轨迹序列τ={s0,a0,r0,s1,a1,
并通过优化动作选择策略πat|st获得最大累积折扣奖励:
其中 γ为折扣因子,使智能体在当前时刻t所获得的累积折扣奖励,随时间增长逐渐减弱.由于难以计算累计反馈精确值,利用期望近似求解累积反馈,得到状态值函数Vπ(st)与动作值函数Qπ(st,at),在时刻t获得状态st及该状态下选择动作at时的累积反馈为
当智能体获取当前状态st根据策略选择动作at后获得下一时刻环境状态st+1,可得到
其中ps(·)为当前环境的状态转移概率函数.在确定性环境中,即ps(·)已知时,强化学习期待通过最大化动作值函数求解强化学习模型最优策略.在状态转移概率未知的自由环境中,可利用蒙特卡罗或时序差分理论,通过策略迭代的方式求解最优化策略,策略评估阶段通过求解该策略下的值函数,评价当前策略,并实现策略改进.然而,传统策略评估模型,仅能求解离散样本空间学习问题.
针对连续空间探索问题,AC 模型借助深度神经网络强大的非线性表达能力,构建策略网络π(at|st;θ)作为“演员”网络,替代原始策略评估方法;同时,利用价值网络V(s;θv)作为“评论家”网络,用于实现动作选择策略改进.参数 θ和 θv为线性函数或深度神经网络等模型参数.
智能体在与环境交互多个时间步T之后使用经验数据,根据优化目标计算网络参数,优化目标由3个损失函数构成:策略损失函数、值损失函数、熵损失函数,其中策略损失函数J(π)的梯度表达为:
其中A(st,at;θ,θv)为优势估计函数.定义dπ(s)=Pr(st=s|s0,π)为当前策略 π下的稳定状态分布.根据强化学习最大化累积反馈的目标,此时计算梯度,并实现梯度上升.AC 框架中可利用多步TD(FTD(λ))更新价值网络,估计当前状态价值,该优化目标中的损失函数为:
其中k为交互过程的采样步数,其上限为单次网络更新采样的序列长度.
AC 为避免智能体陷入局部最优解,鼓励智能体充分探索,定义熵损失函数H(π(st;θ′)),其中H(·)为策略网络 π的熵,结合式(5),得到AC 模型中智能体总体损失函数:
其中 α 与 β为平衡参数,分别控制价值网络更新幅度与熵正则项对学习性能影响力度.最大化该损失函数使智能体获得最大累计反馈,提升学习效果.
1.2 异步优势演员-评论家模型
A3C 框架基于AC 的强化学习模式,并进一步在多进程中复制相同结构智能体,构建一主多从的网络框架,包含主智能体Learner 及其他多个具有相同网络结构且互相独立的子智能体Worker,并行地在某一环境中探索并分别与环境交互采样.A3C 利用Worker 对Learner 的异步更新实现大规模网络并行探索.A3C 框架具体结构及执行流程如图1 所示,首先,所有智能体在环境中探索一定时间步后,其中某一Worker 根据自身网络参数 θW及定义的损失函数J(V,π)求解得到参数梯度∇θW,并将其直接迁移至Learner;其次,Learner 结合自身学习状态,根据θL+η∇θW更新自身网络参数;最后,Learner 回传更新后的网络参数 θL给等待更新的Worker,Worker 使用回传的 θL替换目前网络参数 θW并继续与环境交互.上述过程以异步方式在各个线程Worker 中同时进行并不断迭代,直至智能体模型收敛,该方式可有效利用并行计算资源在短时间内积累到大量经验数据,加速模型训练.
2 本文方法
A3C 框架通过智能体分布式训练、参数异步更新实现对环境高效探索.然而,复杂环境中多Worker学习性能的高方差现象将导致Learner 难以获得全局最优性能,导致并行学习资源浪费.同时,此种大规模并行强化学习网络难以快速迁移、应用到移动平台或低功耗近端平台.本文提出监督探索的A3C 模型压缩方法——紧凑A3C 框架(compact_A3C),充分抽取大规模并行强化网络知识,构建“教师网络”指导小规模“学生网络”,对最优策略探索,Compact_A3C 框架及学习流程如图2 所示.首先,冻结并评价预训练并行网络中所有Worker (第1 步);其次,利用softmax 函数将所有Worker 在环境中表现转化为Learner 参数迁移概率,完成最优化“教师网络”构建(第2 步);最后,借助“教师网络”智能体监督小规模“学生网络”前期环境探索,并建立辅助损失函数鼓励“学生网络”自由探索,提升“学生网络”学习性能(第3 步).
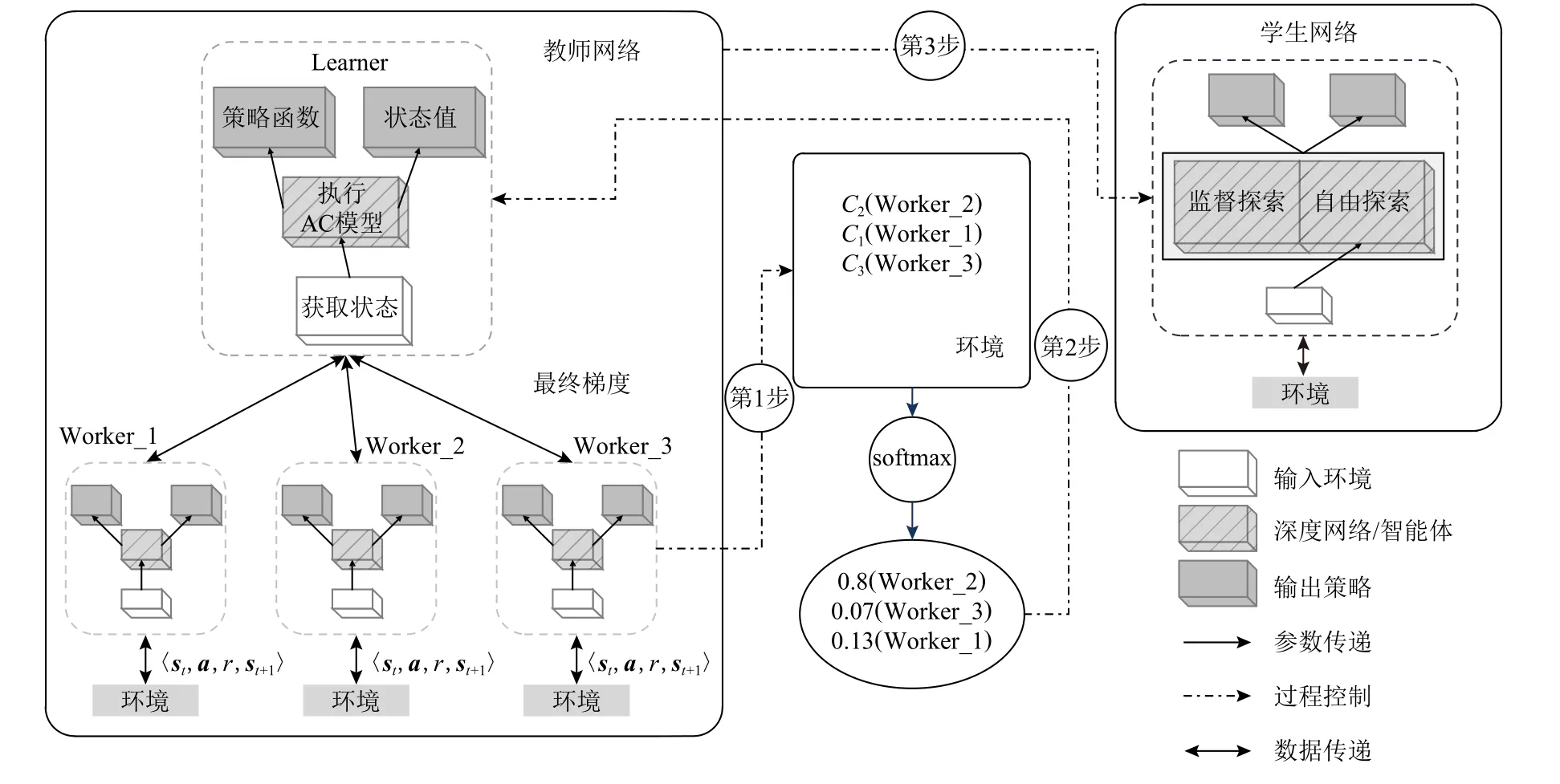
Fig.2 The framework of our proposed method图2 本文方法框架结构
Compact_A3C 框架使“学生网络”智能体行为策略在与环境交互采样轨迹上尽可能与“教师网络”智能体行为策略接近,并允许该辅助损失在整体训练过程中的影响随时间变化,以便“学生网络”智能体可以逐渐增加对强化学习目标(最大化累计反馈值)的关注.“学生网络”受预训练“教师网络”在最优策略上的监督及指导,实现网络参数量压缩,可使其在某些复杂环境中的学习性能超过初始“教师网络”性能.
2.1 全局最优策略抽取
Compact_A3C 利用留存在各个异步进程上结构相同、参数不同的智能体模型,充分利用A3C 并行框架中全部Worker 对环境探索过程所获取的知识.首先,冻结并行网络中所有K个Worker 网络参数,将其转换为确定性策略,并将其投入训练环境中完成学习性能评估.根据不同环境定义性能评分标准,对子智能体性能量化,例如,保存并统计经典Atari-Breakout 环境下Worker 的表现评分为Ck;之后,本文将量化Ck转换为激活概率,作为Learner 每轮更新模型抽取概率,避免了原始A3C 训练过程高方差问题产生的性能影响.同时,解决原始A3C 框架中学习资源浪费,即Learner 智能体更新非全局最优模型参数等问题.
本文中利用非线性激活函数softmax 实现计算及概率转化,具体为:
其中pk为该智能体每轮被抽取到的概率.转化过程如图3 所示,假设K=3,首先,利用式(7)将每一Worker 在具体场景中表现转化为用于更新Learner的概率表达;其次,将全概率空间映射为固定范围整数空间pk∈(0,1)→Z,并将其划分为对应Worker 的K个区域;最后,从该整数集合中随机取值得到对应的Worker,并更新Learner 模型.
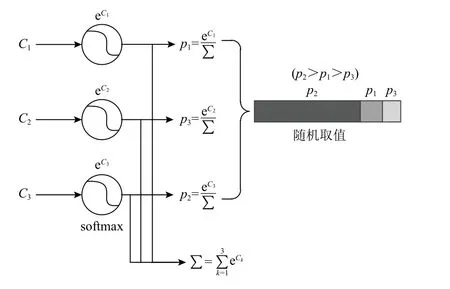
Fig.3 Parameters updating,probability transformation and random selection图3 参数更新、概率转化和随机抽取
上述策略抽取方法避免了一般的性能排序方法,在每轮Learner 参数更新过程中仅考虑最优模型产生的资源浪费.该方法不仅可提升性能好的Worker 被选中的概率,同时,保留并行环境中其他Worker 已获得的知识,高效利用历史探索信息.
本文所提出的全局最优策略抽取方法相比于原始更新方式更为有效.假设,Compact_A3C 框架处于最差情况,即A3C 网络中所有Worker 均达到最优性能时,最优Worker 智能体抽取概率为pi=m,其中由文献[35]可知,模型处于高方差环境.因此,存在选取某一 Worker 的概率为=m-δ,δ ≥0,结合式(7)可得到≤pk.由此可知,本文提出的全局最优化模型抽取方法性能优于原始A3C 学习过程及模型更新.
因此,Compact_A3C 为构建用于知识抽取的更优化“教师网络”提供了前提.保留其他Worker 智能体模型被选取的可能性,使并行网络探索知识得到更为充分地应用.
2.2 监督探索
针对提升“学生网络”智能体性能,本文提出监督探索的学习方式.该方法借助“教师网络”前期积累知识,避免“学生网络”对无效环境探索,快速获得更优化策略.此前,有学者提出策略蒸馏(policy distillation)[37]方法解决强化学习网络压缩问题,通过预训练教师智能体,获得策略 πtea,并生成探索轨迹 τ,每个轨迹包含一系列状态(st)t≥0,在该轨迹上将学生智能体策略 πstu与 πtea匹配,其主要通过构建近似模型实现“学生网络”对“教师网络”的知识复制.Policy Distillation 难以与A3C 模型异步更新过程结合,无法直接迁移使用.同时,其未考虑对“学生网络”智能体自主学习性能的训练,使“学生网络”难以达到与“教师网络”相当或更好的学习性能.本文针对该问题,提出监督探索的A3C 模型压缩过程,“教师网络”智能体监督“学生网络”前期环境探索,避免负向知识积累,指导最优策略学习.同时,鼓励“学生网络”智能体最大化自身与环境交互的累计奖励值,提升学习性能.
定义“学生网络”智能体的探索目标为最大化策略与环境交互采样轨迹累积奖赏值的期望Eπstu(R)和累积反馈值.“学生网络”智能体依据at~πstu,从策略 πstu中采样得到动作.基于策略模型求解的强化学习过程中,利用上升梯度求解更新目标损失函数JRL(θstu,s,t),同时,为实现监督过程,利用“教师网络”智能体与“学生网络”智能体策略之间的KL 散度,监督“学生网络”智能体对未知环境的前期探索,表示为
为鼓励“学生网络”自由探索,提升学习能力与强化网络性能,本文方法松弛监督项,具体表达为:
其中k为模型训练迭代轮数.λk控制“教师网络”智能体的策略对“学生网络”智能体影响.该方法使“学生网络”智能体避免初始阶段自由探索获得的稀疏奖赏值信号,进而获得稠密反馈.同时,λk随着迭代轮数k的递增而衰减,以确保“学生网络”智能体能够将其优化重点逐渐转移到稀疏奖赏值rt的反馈上,监督探索方法可以快速训练“学生网络”智能体求解全局最优策略,得到Compact_A3C 目标的总体损失函数为:
其中J(πstu)为“学生网络”最大化累计反馈,θstu为“学生网络”智能体网络参数.Compact_A3C 利用DKL(πtea(a|st,θtea)‖πstu(a|st,θstu))监督探索目标,使“学生网络”智能体行为与“教师网络”智能体趋近,保证模型的状态估值更加准确.同时,式(10)中H(πstu(st;θstu))部分为熵正则,用于鼓励“学生网络”自由探索获得最优化策略.求解策略梯度为:
其中Atea(·)为“教师网络”智能体的优势估计函数.
Compact_A3C 中监督探索损失相当于“教师”智能体策略对“学生”智能体学习的鼓励行为,与熵正则化并不使智能体策略收敛到最大化熵目标一致,该方法目标不使“学生”智能体策略完全收敛到“教师”智能体策略,仅为“学生网络”最优化策略学习提供方向.因此,熵正则化角度为本文方法提供了较好的解释,即在总体目标优化的同时使输出尽可能随机,并尽可能鼓励智能体在最优策略初始方向上的探索,使“学生网络”得到优于“教师网络”的学习性能.Compact_A3C 算法描述为:
3 实验结果及分析
本文选择不同规模及复杂度的深度强化学习环境验证所提出方法的有效性,包括Gym Classic Control 与Atari 2600 环境.将原始A3C 模型在所有验证环境中预训练,并根据所提出的全局策略抽取方法更新A3C 中Learner 网络,构建最优化“教师网络”.为保证实验全面性,本文分别选择45%及20%网络参数压缩比构建小规模“学生网络”.本文中实验环境为I7-8 700 处理器,16GB-RAM,RTX2070 独立显卡,并使用Pytorch 深度学习库构建模型框架.
为保证实验公平性,本文利用相同环境下实验验证的方式进行超参数选取.根据第2 节对Compact_A3C 框架的描述,结合式(9)可知参数 λ控制“教师网络”对“学生网络”监督强度,λ的选取将影响网络学习效果.本文对比了3 类参数设置方式:分段衰减、指数衰减、线性衰减,并在Cartpole 环境中进行了实验分析与对比,如图4(a)~(c)所示,其中设置所有参数衰减的总训练回合数为800,训练初始值λ=0.5.依据不同衰减形式:1)分段衰减,λ在100回合、300 回合、500 回合依顺序取值为0.25,0.1,0;2)指数衰减,每回合将 λt乘以常数衰减因子0.9,即λt+1=0.9λt;3)线性衰减,每回合将 λt减去常数衰减因子0.001,即λt+1=λt-0.001.根据3 种不同的衰减形式,在环境中训练模型,并得到反馈曲线,如图4 所示.图4(c)中所选择的线性衰减方式在前期逐渐弱化监督与鼓励自由探索过程,获得了最好的效果.因此,在后续所有环境实验中,本文中均设置参数 λ取值为线性衰减.
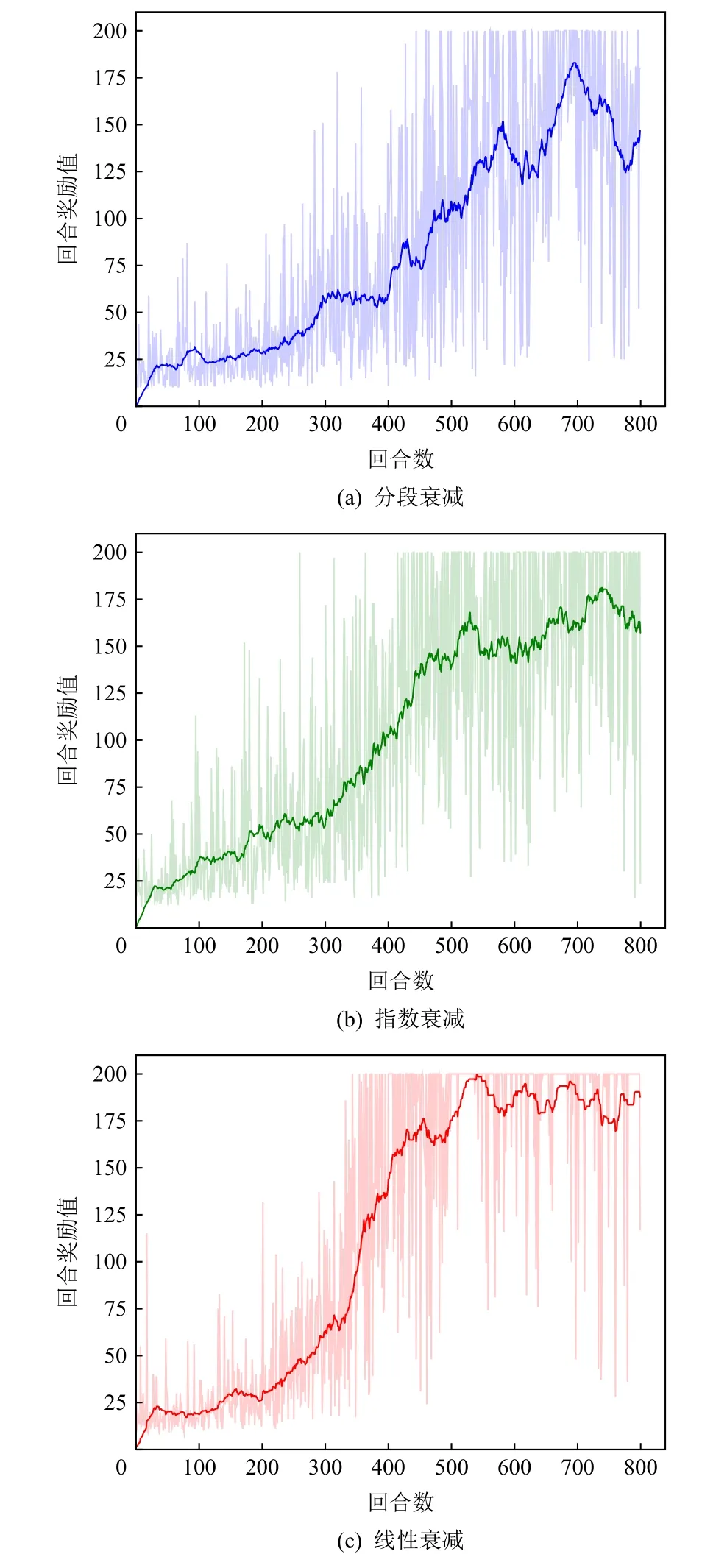
Fig.4 Comparison of reward curves with different decay forms in Cartplot environment图4 Cartplot 环境中不同衰减方式下反馈曲线对比
3.1 Gym Classic Control 环境
本文在Gym Classic Control 环境类别中选取2 个常用的强化学习验证环境:CartPole 和MountainCar,如图5(a)(b)所示.同时,设置预训练的并行网络架构由4 个Worker 及1 个Learner 组成,为后续构建“教师网络”提供条件.分别建立压缩比为45%与20% 规模的“学生网络”,分析及对比本文所提出方法的有效性.在Gym Classic Control 类别环境中“教师网络”与“学生网络”模型结构设置如表1 所示,网络参数设置如表2 所示.

Table 1 Structure of Environment Network in Gym Classic Control表1 Gym Classic Control 环境网络结构
Fig.5 Gym Classic Control environment effects图5 Gym Classic Control 环境效果
CartPole 为一阶倒立摆环境,通过智能体左、右移动控制滑块保证杆子竖直,当杆子与竖直夹角超过15 度或滑块位置超出显示范围,则判定控制失败,环境重启下一轮,每次重启后智能体初始状态会略有不同,可视化场景如图5(a)所示.根据场景描述,可将状态空间抽象为由浮点数构成的物理变量st=(位移,速度),智能体动作空间由代表可用于左、右移动控制的整型数构成,at=(左移(0),右移(0)),反馈值变化定义为每坚持1 帧获得+1 反馈.
MountainCar 为小车爬山环境,智能体左、右移动控制小车自谷底到达右山峰峰顶,小车如从两边斜坡下滑则判定控制失败,环境重启下一轮,可视化场景如图5(b)所示.根据场景描述,可将状态空间抽象为浮点数表示的物理变量st=(位移,速度),智能体动作空间由可用于移动控制的整型数代表构成,at=(左移(0),不动(1),右移(2)),反馈值变化定义为每前进1 帧,若未成功登顶得到-1 反馈.
本文实验中将所有待比较智能体训练至收敛后,转换为确定性策略在原环境中运行,将运行10 个回合的平均得分作为智能体性能评价指标进行分析,并对比“教师网络”及不同压缩比下“学生网络”执行结果,如表3 所示,学生网络包含较少参数量仍可达到与教师网络相当的效果.图6(a)为CartPole 环境中反馈曲线随回合数的变化情况,本文所提出方法在“学生网络”压缩比为45%时,由于“学生网络”前期探索阶段受“教师网络”监督,可快速学习到最优化策略,反馈曲线在回合数为400 即可达到“教师网络”处于1 100 回合数时的反馈值.同时,当网络压缩比达到20%时仍可在回合数为800 达到相当的反馈结果.图6(b)为MountainCar 环境反馈曲线对比结果,由 图6(b)中可见,“学生网络”即使在压缩比达到20%的情况下仍实现了反馈曲线快速上升,该结果可验证所提出“教师网络”的前期监督,为最优化策略探索提供了显著的指导作用.

Table 3 Performance Comparison among Networks in Gym Classic Control Environment表3 Gym Classic Control 环境中的网络性能对比
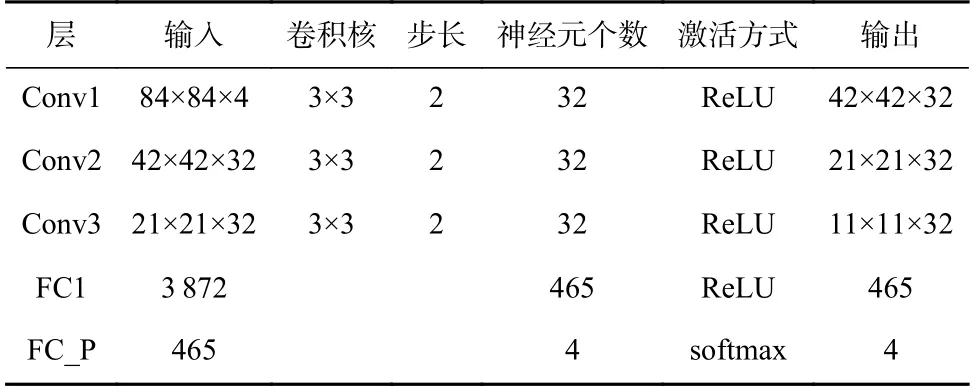
Table 5 Student-Network 1 Structure in Atari 2600 Environment表5 Atari 2600 环境学生网络1 结构
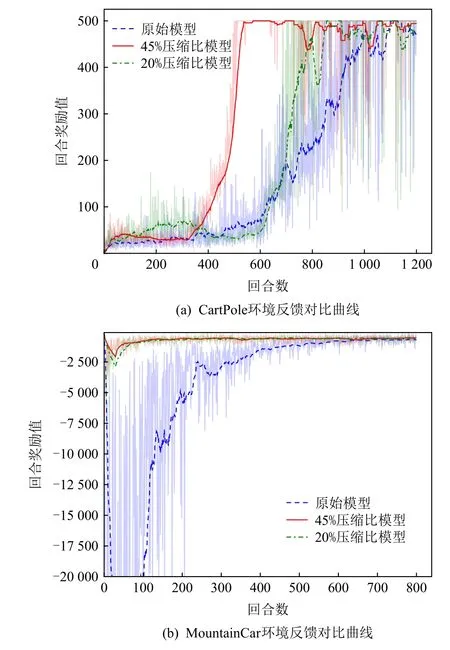
Fig.6 Comparison of reward curves in Gym Classic Control environment图6 Gym Classic Control 环境反馈曲线对比
3.2 Atari 2600 环境
本文选取Atari 2600 中3 个经典图像环境:Pong,Breakout,SpaceInvaders,并构建6 个Worker 及1 个Learner 组成的预训练并行框架,验证本文所提出方法的效果.该类别的3 个环境下“教师网络”与“学生网络”结构如表4~6,深度网络参数如表7 所示,大参数量网络结构提供了更好的图像环境特征表达,然而,也为该类模型的近端迁移带来了阻碍.针对该类环境建立的“学生网络”压缩比仍为45%与20%.
Pong,Breakout,SpaceInvaders 均源于Atari 2600环境,需要智能体按照游戏规则操控环境中智能体,根据规则定义尽可能获取更高得分,当智能体触发失败的判定(生命数归零或连续减分),游戏重启进入下一回合,环境可视化如图7 所示.该类环境的状态空间为具体游戏界面表示的210×160×3 RGB 图像,动作空间由整型数组成,反馈规则由具体环境确定,根据具体任务选取部分动作,组成本环境动作空间,其中Breakout 环境中动作空间为at=(不动(0),开火(1);右移(2),左移(3)),Pong 应用环境中动作空间为at=(不动(0),开火(1);右移(2),左移(3);右开火(4),左开火(5)),SpaceInvaders 应用环境中动作空间为at=(不动(0),开火(1);右移(2),左移(3);右开火(4),左开火(5)).
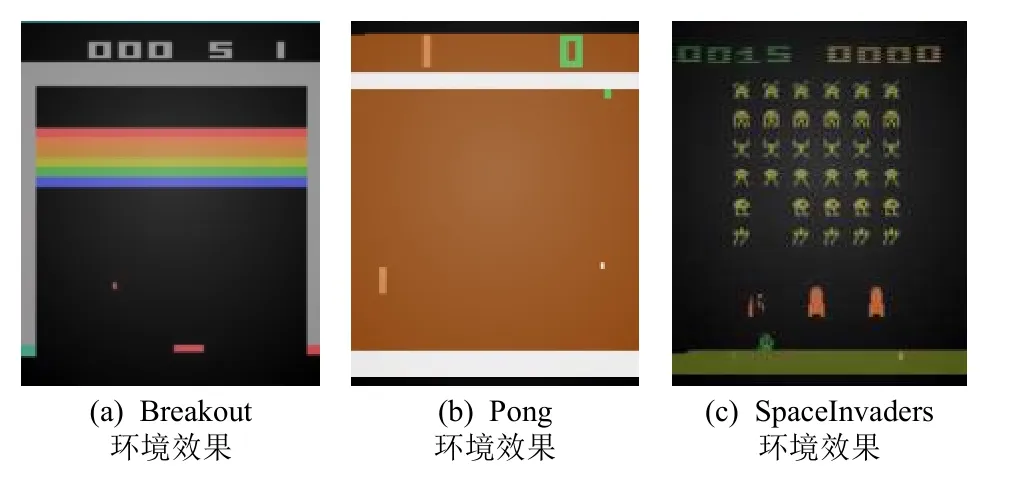
Fig.7 Atari 2600 environment effects图7 Atari 2600 环境效果
Atari 2600 类环境下反馈曲线如图8 所示,其中Pong 环境的“学生网络”参数量在压缩比仅20%的情况下即可达到与“教师网络”智能体相当的性能及水平.该实验结果可表明较大规模网络在解决该类问题中存在一定的资源浪费,同时,对小规模“学生网络”的有效训练,说明了其近端可迁移及可使用性.Breakout 环境中的2 类压缩比下所构建的“学生网络”性能均超越了“教师网络”智能体表现,验证了所提出方法的有效性.在SpaceInvaders 环境中,压缩比为45%的“学生网络”智能体表现超越了“教师网络”智能体,然而,20%参数量“学生网络”智能体性能对比“教师网络”智能体性能存在一定落差,在复杂环境中强化学习模型需要更复杂网络建立状态特征描述.同时,在3 个环境中模型均获得了较高的采样率,并在SpaceInvaders 与Pong 环境中的采样率显著高于在Breakout 环境中的.
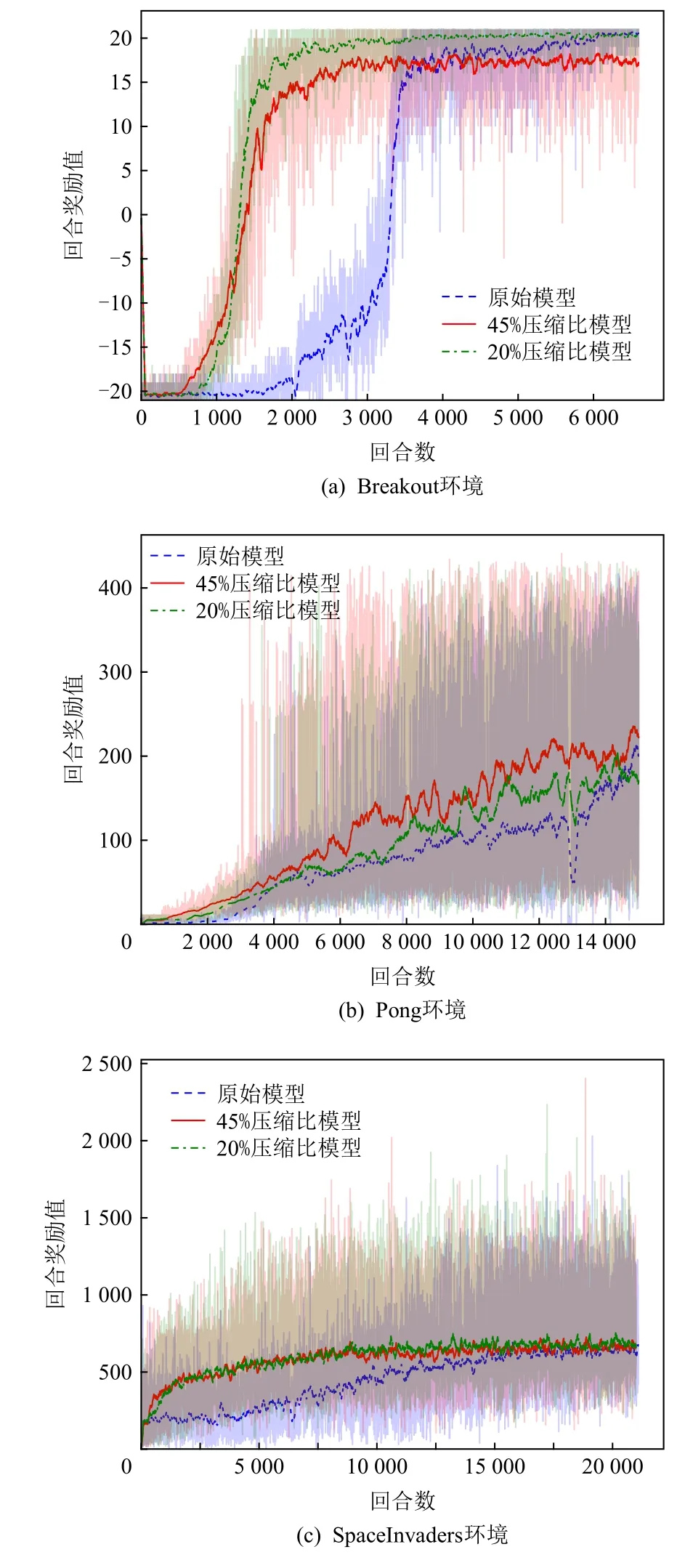
Fig.8 Comparison of reward curves with different compression ratios in Atarti 2600 environment图8 Atari 2600 环境中不同压缩比反馈曲线对比
由表8 中所统计的网络性能结果可见,“学生网络”智能体均可达到与“教师网络”智能体性能相当的效果,同时,在“教师网络”监督指导下学生智能体获得了更高的评分并发挥了更好的自由探索性能.
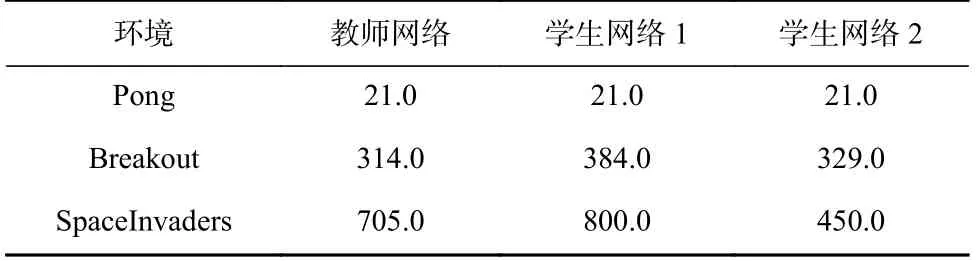
Table 8 Performance Comparison among Networks in Atari 2600 Environment表8 Atari 2600 环境中网络性能对比
4 结 论
本文针对A3C 模型在学习过程中对资源利用率低且难以近端迁移等问题,首次提出监督的模型压缩及知识抽取模型Compact_A3C.首先,该模型通过冻结并行网络中所有子智能体网络参数,利用原始环境评价学习性能,并量化为评分后转化其为主智能体模型的逐步更新选取策略概率,实现“教师网络”全局最优化模型更新;其次,利用“教师网络”监督小规模“学生网络”,为最优化策略提供前期探索相关知识与指导;最后,通过线性损失函数衰退控制知识遗忘,鼓励“学生网络”自由探索,实现网络压缩.本文在目前较为流行的Gym Classic Control 与Atari 2600 环境中验证所提出的方法,“学生网络”在压缩比为45%及20%的情况下均达到了与“教师网络”一致的学习性能,并在Breakout 与SpaceInvaders 图像环境中取得了比“教师网络”更好的效果,该实验结果验证了本文提出的方法针对A3C 深度强化模型压缩的有效性,同时,本文公开了所提出方法的源代码①https://github.com/meadewaking/Compact_A3C.,为未来大规模并行深度强化学习模型的近端应用提供了一定的思路与前提.
作者贡献声明:张晶负责模型提出、算法设计及论文撰写;王子铭负责模型优化、算法实现、实验验证及论文初稿撰写;任永功负责模型思想设计及写作指导.

