3种栎属树种单木生长模型及树皮厚度模型研究
谭灿灿,聂 稳,刘逸夫,王 亚,董 遥,,黄睿智,,刘建锋,史胜青,常二梅,赵秀莲,江泽平,贾子瑞
(1.中国林业科学研究院 森林生态环境与自然保护研究所,北京 100091;2.中国林业科学研究院 林业研究所,北京 100091)
构建树木生长模型对林业生产和经营管理有重要意义[1]。根据立木生长的预估结果,生长模型可分为全林分模型、径阶生长模型、单木生长模型[2]。近年来,混合效应模型被广泛应用于林业中,陈哲夫等[3]以湖南马尾松Pinusmassoniana次生林为研究对象,比较基础模型与混合效应模型的优劣,得出含样地效应的混合效应模型拟合效果和预测精度均优于基础模型,具有更高的适用性。树皮对植物起到重要的保护作用[4]。研究发现树皮厚度会随着地理格局发生变异[5]。且树皮大约占木材体积的12%~20%,不同树种间存在一定差异[6]。精准测算树皮厚度对林业生产至关重要。
栎属Quercus约450 种[7],是壳斗科Fagaceae 最大的属,分布极为广泛。中国有51 种14 变种1 变型[8],它们分布于全国各地,是组成森林的重要树种。其中栓皮栎Q.variabilis、麻栎Q.acutissima、槲栎Q.aliena既是中国主要生态树种,又具有重要的经济价值。目前,已有不少针对栎属植物生长模型的研究[9-12],发现栎树树高最优模型以理查德(Richards)模型和考夫(Korf)模型拟合效果最佳,材积最优模型以Richards 模型最佳,胸径最优模型以坎派兹(Compertz)模型最佳。以上模型能较好地拟合栎树的生长,但缺少不同区域、立地条件对林木生长影响的考虑。本研究以栓皮栎、麻栎、槲栎3 种栎属植物为研究对象,通过搜集早期主要分布区(山西、河南、山东和陕西等地)的解析木数据,拟合单木树高、材积、胸径和树皮厚度生长方程,以期准确预估3 个树种林分的生长过程,并为其在不同生境地点合理的森林经营管理提供理论依据。
1 材料与方法
1.1 数据收集
从全国及各省份主要树木生长量汇编书籍《中国主要树木生长量汇编(第1 辑)》《中国主要树木生长量汇编(第3 辑)》《山西省主要树木生长量汇编》《陕西主要树种树木生长资料集》收集槲栎、麻栎、栓皮栎3 个树种的树干解析数据。提取与汇总树木生长过程信息,槲栎、栓皮栎以10 a 为1 个龄阶,麻栎以2 a 为1 个龄阶。为了更好地模拟效果,数据的2/3 用于拟合模型,数据的1/3 用于验证。将树高(H)、材积(V)、胸径(DBH)与树龄(Y)进行拟合,树皮厚度(BT)与胸径进行拟合,建立栎树人工林树高、材积、胸径、树皮厚度模型。
各采集地1981—2010年的基本气候数据由国家气象科学数据中心(http://data.cma.cn/)提供,统计各采集地的年平均降水量与年平均气温,作为栎属植物生长的气候数据。
1.2 单木生长模型的构建
林木的生长方程是描述树木各生长量随林分年龄生长变化规律的数学模型,反映的生长量变化大致呈“S”型。根据林木生长特征,用理查德、坎派兹、逻辑斯蒂(Logistic)、单分子式(Mistcherlich)等4 个理论生长方程,以及1 个拟合效果较好的经验方程(Weibull modified,修正威布尔)作为栎属植物单木树高、材积和胸径生长的基础模型;线性模型(Linear)、二元一次线性模型(Binary linear)、双对数模型(Double logarithmic)等3 个胸径处树皮厚度模型用于树皮厚度变化模拟。模型的拟合及其参数计算在CurveExpert 2.6 软件完成。本研究收集了各树种解析木树高、胸径和材积的数据,利用定期平均生长量代替了连年生长量,因此出现 0~10 a 的连年生长量和平均生长量相等的情况。
1.3 模型验证与评价
为了对模拟结果做出客观合理的评价,本研究采用决定系数(R2) 和赤池信息准则(Akaike information criterion,AIC)对拟合模型精度进行评价,R2越大,AIC 越小说明模型拟合效果越好;采用均方根误差(RMSE)、平均决定误差(MAE)、平均误差(ME) 等3 个指标作为模型的精度检验指标。用SPSS 26 统计分析,Origin 2022 作图。
2 结果与分析
2.1 槲栎生长特征分析及生长模型构建
2.1.1 槲栎生长特征分析 如图1所示:槲栎在山西省与河南省的树高、材积、胸径总生长量随树龄的增大而增加。山西省树高连年生长量与平均生长量(后用“2 种生长量”)先增大后减小,2 种生长量在30 a 时达到最大值,分别为0.250 与0.214 m。30 a 后2 种生长量快速下降,且连年生长量下降速度大于平均生长量。河南省树高2 种生长量最大值出现在10 a,为0.371 m,随后2 种生长量逐渐减小。山西省胸径连年生长量30 a 时达到最大值,为0.386 cm,平均生长量在40 a 时最大,为0.263 cm。60 a 后2 种生长量趋于稳定。河南省胸径2 种生长量在30 a 时最大,分别为0.423 与0.366 cm,随后逐年下降。山西省材积2 种生长量总体上保持随年龄的增加而增大。河南省材积2 种生长量在90 a 时发生减小的现象,但不能确定其变化趋势,还需更长年限的观测。两省材积连年生长量与平均生长量在统计年限内均没有出现交点,说明100 a 槲栎还未达到数量成熟龄,还不能确定主伐年龄。两省材积的总生长量一直处于上升的状态,没有出现变缓现象,说明100 a 时的槲栎依旧处于生长旺盛阶段。
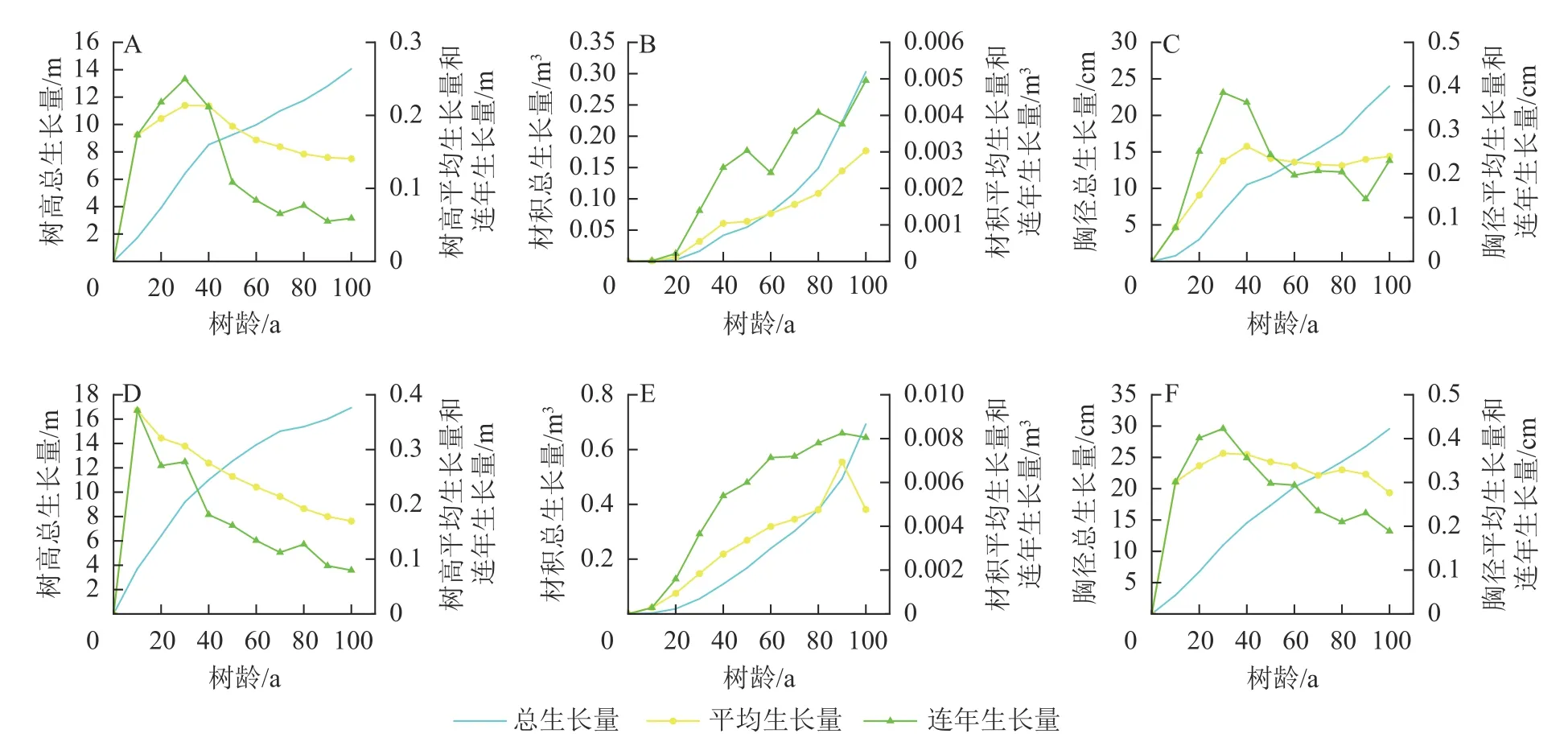
图1 不同分布区槲栎生长过程曲线Figure 1 Growth curves of Q. aliena in different distribution areas
2.1.2 槲栎生长模型构建 由表1可知:在拟合精度上,山西省拟合效果更佳,树高最优生长方程为逻辑斯蒂模型,R2达0.94,材积最优生长方程为坎派兹模型,R2为0.784,胸径最优生长方程为修正威布尔模型,R2为0.928。河南省槲栎拟合情况则较差。山西省与河南省槲栎树高、材积与胸径拟合最优模型均相同,分别为逻辑斯蒂模型、坎派兹模型与修正威布尔模型,可以用于槲栎生长过程模拟。

表1 槲栎生长拟合模型与检验Table 1 Growth fitting models and testing of Q. aliena
2.2 栓皮栎生长特征分析及生长模型构建
2.2.1 栓皮栎生长特征分析 如图2所示:两省栓皮栎树高、材积、胸径随树龄的增加而增大。前20 a河南省栓皮栎树高2 种生长量逐渐增加,20 a 达到最大平均生长量(0.378 m)和最大连年生长量(0.400 m),20 a 后逐年变小。陕西省树高2 种生长量在10 a 时最大,10 a 后逐年变小。河南省栓皮栎胸径在30 a时2 种生长量达到最大值,分别为0.584 与0.466 cm,随后2 种生长量逐年减小,于60~70 a 时趋于平稳。陕西省栓皮栎胸径2 种生长量在20 a 达到最大值,分别为0.564 与0.498 cm,20 a 后逐年减小。河南省栓皮栎材积连年生长量在前40 a 迅速增大,40 a 后趋于平稳,材积平均生长量始终保持随树龄增加而增大,增加速度慢于连年生长量。陕西省材积2 种生长量随树龄增加而增大,且连年生长量大于平均生长量。两省栓皮栎在70 a 内连年生长量与平均生长量均未相交,说明70 a 时栓皮栎还未达到数量成熟龄,即还不能确定主伐年龄。两省的材积总生长量随着树龄增加而增大,其增长呈越来越快的趋势,说明70 a 时两省栓皮栎还处于生长旺盛阶段。

图2 不同分布区栓皮栎生长过程曲线Figure 2 Growth curves of Q. variabilis in different distribution areas
2.2.2 栓皮栎生长模型构建 由表2可知:河南省栓皮栎树高、材积、胸径最适的模型分别为修正威布尔模型、坎派兹模型、坎派兹模型。陕西省栓皮栎树高、材积、胸径最适的模型分别为逻辑斯蒂模型、逻辑斯蒂模型、单分子式模型。相较下,河南省栓皮栎各生长因子的拟合效果优于陕西省,其中河南省树高拟合最佳的修正威布尔模型R2为0.906,且各检验指标都较小,优于其他拟合效果。并且河南省拟合的数据量更大,更能反映栓皮栎的生长过程。因此,选择河南省单木生长拟合结果代表栓皮栎生长过程。

表2 栓皮栎生长拟合模型与检验Table 2 Growth fitting models and testing of Q. variabilis
2.3 麻栎生长特征分析及生长模型构建
2.3.1 麻栎生长特征分析 如图3所示:山东省麻栎树高2 种生长量均在0.6 m 上下波动,平均生长量最大值为0.694 m,最小值为0.613 m;连年生长量最大值为0.753 m,最小值为0.475 m。麻栎胸径平均生长量0~6 a 呈随树龄增加而增大,6 a 后保持在0.6 cm 上下;连年生长量在0~4 a 迅速增加,4 a 时连年生长量达最大值,为0.850 cm,4~8 a 逐渐减小,8 a 后连年生长量存在一定起伏,保持在0.6 cm 左右。麻栎材积2 种生长量在前4 a 增长较慢,4 a 后材积连年生长量迅速增加,18 a 时达0.007 m3,材积平均生长量随着树龄的增加而增大,但增加量始终小于连年生长量。麻栎材积总生长量随着树龄增加而增大,其增长呈越来越快的趋势,16 a 后有所变缓。麻栎树高、材积与胸径总生长量始终保持增大,且没有变缓的趋势,但由于解析木测得的年限较短,并不能代表麻栎整个生长过程,若要进一步揭示麻栎生长过程特征应结合树高树龄麻栎生长信息综合分析。

图3 山东省麻栎生长过程曲线Figure 3 Growth curves of Q. acutissima in Shandong Province
2.3.2 麻栎生长模型构建 由表3可知:麻栎树高拟合效果均较好,R2在0.918 以上,通过比较AIC 与其检验指数,单分子式模型的AIC 为-3.837,检验指数整体表现较好,因此单分子式模型为麻栎树高拟合效果最佳的模型。同理,麻栎材积最适模型为逻辑斯蒂模型,其R2=0.719 和赤池信息准则(AIC=140.673)均表现最佳。麻栎胸径最适模型为修正威布尔模型和逻辑斯蒂模型,决定系数修正威布尔模型稍大于逻辑斯蒂模型,在AIC 值和检验指标方面逻辑斯蒂模型表现稍好。因此,2 种拟合结果均可代表胸径的生长过程。

表3 麻栎生长拟合模型与检验Table 3 Growth fitting models and testing of Q. acutissima
2.4 气候因子对栎树单木生长过程的影响
选择80 a 时槲栎与60 a 时栓皮栎各生长因子数据与气候因子数据进行分析,探究气候因子对单木生长的影响。由图4~5 可知:槲栎分布区山西省和河南省的年降水量与气温差异显著。两省在树高、材积与胸径上均存在显著差异。栓皮栎分布区河南省和陕西省在平均气温和最高气温存在差异,年降水量没有差异。栓皮栎树高、材积与胸径在两省间均无明显差异。说明气候差异会影响槲栎生长过程,而不同省份的气候差异未能影响栓皮栎生长。

图4 槲栎和栓皮栎不同分布区气候差异柱状图Figure 4 Climate difference of Q. aliena and Q. variabilis in different distribution area
2.5 树皮厚度模型拟合及检验
由表4可知:槲栎树皮厚度最优模型为双对数模型;麻栎树皮厚度最优模型为二元一次模型;栓皮栎树皮厚度最优模型为二元一次模型。其中,麻栎树皮厚度拟合精度最优,在山东省R2为0.83,2 个省总体水平的R2为0.847,主要原因是麻栎树皮厚度数据集中在20~30 a。栓皮栎在河南省和陕西省的R2分别为0.615 和0.798,因为二元一次模型包含树高和胸径2 个参数,因此栓皮栎树皮厚度更适合二元一次模型。槲栎拟合效果相对麻栎和栓皮栎较差,在河南省和陕西省汇总数据的R2均约0.5。

表4 栎属3 个树种的树皮厚度模型拟合与检验Table 4 Bark thickness model fitting and testing of three Quercus species
3 讨论与结论
本研究以不同分布区栎属3 个树种为研究对象,通过对栎树树高、材积与胸径进行拟合,探究栎树各生长因子的最适模型。槲栎拟合结果表明:树高、材积、胸径最优模型分别为逻辑斯蒂模型、坎派兹模型与修正威布尔模型。栓皮栎各生长指标的最优模型分别为修正威布尔模型、坎派兹模型、坎派兹模型,其胸径拟合结果与陈亚文[13]对栓皮栎胸径拟合结果不同,陈亚文[13]拟合结果以威布尔模型最优,R2达0.998,分析得知威布尔模型具有4 个参数,从数学角度分析,参数越多拟合结果越逼近,但其缺点是威布尔为经验方程,参数无生物学意义。黄峰等[14]对栓皮栎树高模拟预测结果表明:最优模型为改进的坎派兹模型,改进的坎派兹模型增加了立地因子,提高了栓皮栎的树高预测精度,但该研究是对活立木树高进行的拟合,而不是以解析木为研究对象。麻栎各生长指标拟合结果表明:树高最优模型为单分子式模型,材积最优模型为逻辑斯蒂模型,胸径最优模型为修正威布尔模型和逻辑斯蒂模型。刘小军等[12]对麻栎生长模型的研究表明:逻辑斯蒂模型、坎派兹模型和理查德模型为材积的最优生长模型,与本研究结果相同;胸径最优模型坎派兹模型,树高最优模型考夫模型与本研究存在差异。分析发现该研究麻栎树龄为59 a 的大树,而本研究的麻栎为18 a 的幼树,比较得出:逻辑斯蒂模型方程适用于麻栎的幼树材积估算。对比3 种栎树各生长因子的拟合结果,树高的拟合效果最好,因此树高方程适用于拟合栎树树高生长;材积的拟合效果最差,该结果与萨如拉等[15]对大兴安岭兴安落叶松Larixgmelinii生长拟合的结果一致,这反映了材积受多种因子的影响。在生长特征方面,槲栎与栓皮栎各生长因子的总生长量始终保持随树龄的增大而增加,且分别在100、70 a 时,材积平均生长量和连年生长量未出现交叉点,说明2 个树种仍具一定生长潜力。
在探究气候因子对栎树生长的影响时,气候(气温、降水)差异会导致槲栎树高、胸径、材积的显著差异。该结果与前人的研究结果相似,即树木生长受气温和降水的共同作用[16]。对栓皮栎的分析中,气温的差异未造成生长量的差异,可能是栓皮栎对气温变化不敏感,也可能是两省气温差异较小,未达到极显著水平。在探究气候因子对生长模型的影响方面,单凯丽[17]在研究杉木Cunninghamialanceolata人工林优势木单木生长模型时发现:气候因子会影响杉木生长过程。丁赵炜[18]通过研究湖北省马尾松人工林单木胸径生长模型发现:加入气候因子后能提升模型精度;同样,余黎等[19]研究了气候对单木胸径生长模型的影响,结果表明气候因子能解释胸径生长。综上,将气候因子纳入单木生长模型进行拟合精度会更优。本研究存在的不足为未深入探究影响槲栎各生长的主要气候因子,且模型中未加入立地因子、气候因子等重要参数。
树皮厚度作为树木的又一重要指标,具有重要利用价值。近年来,研究者们致力于开发能准确预测各树种树皮厚度的模型。JOUKO 等[5]在模拟欧洲云杉Piceaabies树皮厚度时发现:树皮厚度与胸径、树高有显著相关性,在木荷Schimasuperba、落叶松、白桦Betulaplatyphylla的研究中也发现了类似的相关性[20-22]。ROSELL[23]在研究18 个地方640 个树种树皮厚度时也发现胸径大小是影响树皮厚度的主要因素。同样,本研究结果得出,能体现树高、胸径与树皮厚度关系的二元一次方程为最优模型。其主要优势是该方法应用简单,需要测定的参数较少,能用于快速测定树皮厚度,但主要的局限性是在模型选择方面直接选用了前人应用效果较好的经验方程,精确度有限,且没区分不同树种、立地类型和林分生长阶段的差异。因此,若想要有效提高建模效率及预测精度,应全面考虑气候、立地、季节性等因素,且针对不同的树种构建专项模型。

