基于TTLS 算法的超声断层成像方法研究

王小婷，王浩全，张瑛

（中北大学 信息与通信工程学院，山西太原，030051）

0 引言

医学影像技术在最近20 年来得到迅速发展，目前超声成像[1]、X射线成像[2]、X射线断层扫描（CT）[3]和核磁共振成像（MRI）[4]等医学成像技术较为常用，成像方法各具特色。

超声波可作为一种携带信息的载体，具有方向性好、穿透能力强和对人体无害等特点，在生物医学领域得到了广泛的应用[5~6]。超声成像根据已知入射波和测得的散射波能够精确重建生物组织声学参量分布[7~8]。由于所检测生物介质的非均匀分布，导致超声散射波函数与生物组织的声学特征函数之间存在非线性关系，需要用迭代近似等方法进行求解[9]，而影响重建效果的另一重要因素为迭代的过程中涉及到的不适定问题的求解，这是此类重建算法的重难点[10~11]。

针对不适定问题导致图像重建质量较差的问题,Pengpeng Xie 等人对比了严重和中度不适定问题下的正则化最小二乘法方法，表明正则化方法具有更好的重建效果[12]。Shaoning Zeng 等人对正则化参数的选取和收敛性进行了研究，用于解决不适定问题[13]。刘超等人提出了进行TTLS正则化的图像重建模型，该方法在图像重建中能够有效去除条形伪影并保护图像细节,同时具有较好的重建质量[14]。刘玉等人运用空间域的TTLS 正则化方法，反演出较高的对比度图像[15]。

本文基于以上研究现状，对TTLS 正则化方法进行改进，通过选取合适的截断参数值k，划分系数矩阵的奇异值，主要部分为较大的和较小的奇异值，引入Tikhonov-Gaussian 方法中的滤波因子为主要思想，对较小奇异值部分进行校正，抑制较小奇异值对正则化解的影响，并将其应用于超声断层成像中，以期获得满意的重建效果。

1 超声成像数学模型建立

超声层析成像通过圆环形换能器对物体散射场信息较为完整的收集，重构物体的内部结构。在已知散射场情况下对描述物体内部特性未知函数进行求解。当散射源与接收器之间为超声波穿过均匀介质时的声场时，方程如下：

式中∇2表示拉布拉斯算子，k0表示介质内的平均波数，为常数，表示入射场。

当发射器与接收器之间有不均匀介质存在产生的声场时，方程如下：

表示所求未知函数。

超声波穿过非均匀介质时产生的压力→场（全场）可以分解为为入射场与散射场

借助格林函数，可把散射场看作为散射点的阵列集合，则超声波入射时的散射场可表示为：

此时物体内部的全场方程可以表示为：

2 TTLS 正则化方法

TTLS 方法是在完全最小二乘法（total least square，TLS）基础上引入截断思想的一种直接正则化方法，可以用于求解逆问题的不适定性。当系数矩阵与数据项误差同时存在的情况下，可以得到两个误差的Frobenius 范数最小值。

在Ax=b法方程的基础上，假设系数矩阵A和右端数据项b都存在误差时，精确的左侧系数矩阵用表示，误差范围下的用A表示，同样，精确的右侧数据项用表示，误差范围内的数据项用表示。单考虑只有右侧数据项存在误差，则最小二乘问题可以表示为：

其中x为成像域散射值矩阵ΔO；A为由未知函数形成的系数矩阵D[[P(t)]]；b为测量得到的散射值 ΔP(s)。

当左侧系数矩阵和右侧数据项同时存在误差时，最小二乘问题可以表示为：

式中||•||F表示Frobenius 范数，为系数矩阵精确值，为数据项精确值。方程式（6）表示为完全最小二乘问题（TLS）。当系数矩阵A和数据项b同时存在误差时，原问题的解可以用增广矩阵(A,b)的奇异值分解表示。

完全最小二乘方法的具体思想如下：

（1）系数矩阵A的增广矩阵(A,b) 可以用奇异值分解

表示为：

其中σi为奇异值，vi为右奇异向量，且相互正交，σ1≥σ2≥ …≥σn≥0，Σ=diag(σ1,σ2,… ,σn)；ui为左奇异向量，且相互正交V=(v1,v2,…,vn)∈Rn×n，V TV=In；U=(u1,u2,…,um)∈Rm×m，U TU=In。

（2）选择截断参数（记为k）k≤min(n,rank(A,b))且满足：

（3）记q=n-k+ 1，对矩阵V进行分块处理：

且满足：V11∈Rn×k，V12∈Rn×q，V21∈Rl×k，V22∈Rl×q。

（4）完全最小二乘问题（TLS）的解表示为：

完全最小二乘问题的范数和残差可以表示为如下：

由方程式(12)及(13)可得，最小二乘解的范数随着k的增大而增大；而随着k的增大，残差的范数却减小了。将截断的思想引入完全最小二乘算法，得到较好拟合效果的TTLS 方法。

截断完全最小二乘法（TTLS）可以表示为：

其中滤波因子fi的形式为：

TTLS 方法中的截断参数k也可以视为正则化参数，该参数的选取直接影响着解的质量。参数k选取较大时，可以实现较好的数据拟合，但对解的范数约束效果较差；k选取较小时，解的约束力效果强，但数据拟合的状态不太理想。因此，选取合适的截断参数k尤为重要。

3 改进的TTLS 正则化方法

Tikhonov 方法将每一项均进行适当程度的滤波，得到原问题的近似求解。通过校正较小的奇异值部分控制噪声的影响，然而对较大奇异值进行校正，会使一定程度的近似解偏离真实的解。

本文采用Gaussian 高通滤波函数作为Tikhonov 正则化的正则化矩阵，Tikhonov-Gaussian 正则化方法的滤波函数可以表示为：

将TTLS 方法和Tikhonov-Gaussian 法相结合对TTLS正则化方法进行改进，在传统的TTLS 方法中，选定合适的截断参数k，将系数矩阵的奇异值分为两部分，较大和较小奇异值，并借助于Tikhonov-Gaussian 方法中的滤波因子，校正较小的奇异值部分，以控制较小奇异值部分对正则化解的影响。改进后的TTLS 正则化方法的方程式可表示为：

因此，本文采用改进的TTLS 算法应用于超声成像，对实验数据进行较小奇异值修正，以获得更稳定的正则化解，得到更好的重建图像。具体步骤如图1 所示。

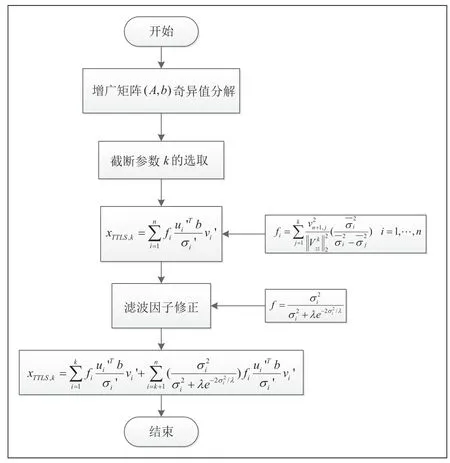
图1 基于改进TTLS 算法的超声断层成像流程图

4 实验结果与分析

本文使用圆环形超声换能器，布置50 个换能器，采用200kHz 的发射波，对35×35pixel的模型图进行算法测试。将物体区域以λ/10=0.75mm 的采样间隔进行均匀采样。

在均方误差、峰值信噪比、图像对比度、信噪比和结构相似性方面对两种算法进行对比分析。本实验仿真平台为MATLAB2016a。使用不同正则化参数的TTLS 方法对模型求解，结果如图2 所示。

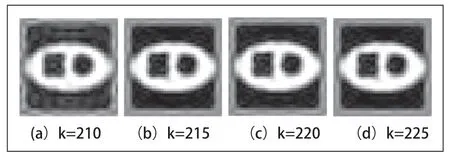
图2 不同正则化参数TTLS 方法重建图

图3中k表示TTLS 正则化参数，可以看到，正则化参数为210 时轮廓逐渐清晰，正则化参数为215 时效果最好，迭代次数较少时所求得的解不能很好的拟合数据，而迭代次数较多时，会导致外部Born 迭代方法发散，适当的正则化参数的选取，可以获得较好的成像效果，解更稳定。

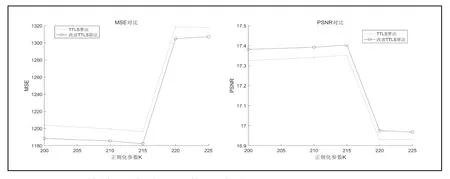
图3 不同算法重建结果量化的比较

本文使用均方误差、峰值信噪比、图像对比度、信噪比和结构相似性5 个指标对算法的性能进行评估。

其中H和W表示图像高和宽；X(i,j)表示待恢复的模糊图像；Y(i,j)为清晰的原始图像；MAX表示图像点颜色的像素最大数值，为255。

式中Cσ表示图像均方根对比度，衡量了图像灰度反差的大小。Iwxh表示宽为w高为h的图，I(x,y)表示图像中指定位置的像素点的值，γIwxh表示图像素平均值。

对两种算法进行图像重建，成像效果分析如图4 所示。

图4 不同算法重建结果图

由此可见，本文采用的改进TTLS 算法重构后的图像能够帮助恢复更多的细节特征，从图像对比度和信噪比等方面可以看出，其重建图像具有良好的成像质量。相同正则化参数k=215 下，相比较于传统TTLS 算法，改进的算法相对误差降低了1.16201%，峰值信噪比提高了0.29132%，信噪比提高了3.0269%，结构相似性提高了1.72531%，图像对比度提高了14.21319%。

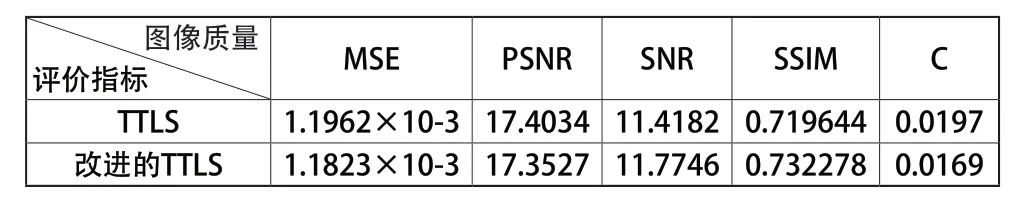
表1 仿真正则化参数为215时两种算法的重构图像精度对比

5 结论

本文在TTLS 方法的基础上，通过选取的截断参数k，划分系数矩阵的奇异值为较大的奇异值和较小的奇异值，并引入Tikhonov-Gaussian 方法中的滤波因子来校正较小的奇异值部分，抑制较小奇异值对正则化解的影响，对传统的TTLS 算法进行改进，并将其用于超声逆散射成像。实验结果表明，传统的TTLS 算法成像质量较差，图像模糊，改进的TTLS 算法重建图像细节特征更为明显，相对误差降低了1.16201%，峰值信噪比提高了0.29132%，信噪比提高了3.0269%，结构相似性提高了1.72531%，图像对比度提高了14.21319%。