桥墩沉降对无砟轨道平顺性的影响分析

段晓晖

（中铁第四勘察设计院集团有限公司，湖北武汉 430063）

0 引言

桥梁结构在我国高速铁路线路中所占比例较大，经桥梁施工及运营部门现场反映：一旦墩台基础发生沉降，梁体会因工后不均匀沉降而下沉，进而通过轨道道床、扣件等部分间的相互作用力，导致钢轨轨面发生变形。根据桥上纵连板式无砟轨道的铺设方式可知，桥墩一发生沉降，与沉降桥墩紧邻的两跨梁桥会由于重力作用而产生垂向位移，轨道结构亦会因桥梁位移发生相应变形，进而影响无砟轨道的平顺性。无砟轨道对下部基础沉降变形尤为敏感。高速铁路基础沉降会导致轨下基础产生较大的变形，轨道平顺性显著降低，引起较大的轮轨动力学响应[1]。基础不均匀沉降直接影响轨道系统安全服役状态和使用寿命，影响旅客的舒适性和行车的安全性，因此需要对下部基础沉降变形进行严格控制[2]。目前已有相关文献，从路基不均匀沉降、桥梁挠曲变形等角度，对无砟轨道的受力、行车安全等方面进行了探讨，并提出了不均匀沉降的限值和轨道整治措施，但是缺少桥墩沉降对无砟轨道平顺性影响的相关研究[3]。因此，分析桥墩沉降幅值和桥梁跨度对无砟轨道平顺性的影响十分必要，为今后高速铁路的设计、施工与运营提供理论参考。

1 计算模型

模型取桥梁为4×32.6m 简支桥梁，模型参数选取如下：60kg/m 钢轨，刚度为30kN/mm 的扣件，弹性模量为200MPa 的砂浆，强度等级为C60 的轨道板混凝土，强度等级为C40 的底座板混凝土，强度等级为C55的梁体混凝土，强度等级C30 的桥墩混凝土。有限元模型中是以实体单元对钢轨、轨道板、底座板及砂浆层架构建模，扣件系统考虑为线性弹簧单元。为模仿沉降作用，对模型中沉降桥墩节点给予垂向位移，并固定约束其余桥墩底部。桥梁和底座板之间的接触关系采用面—面接触单元模拟。

1.1 模型参数

利用有限元建立了纵连板式轨道—桥梁有限元模型，纵连板式无砟轨道与桥梁有限元模型，如图1所示。模型横断面，如图2 所示。

图1 纵连板式无砟轨道与桥梁有限元模型

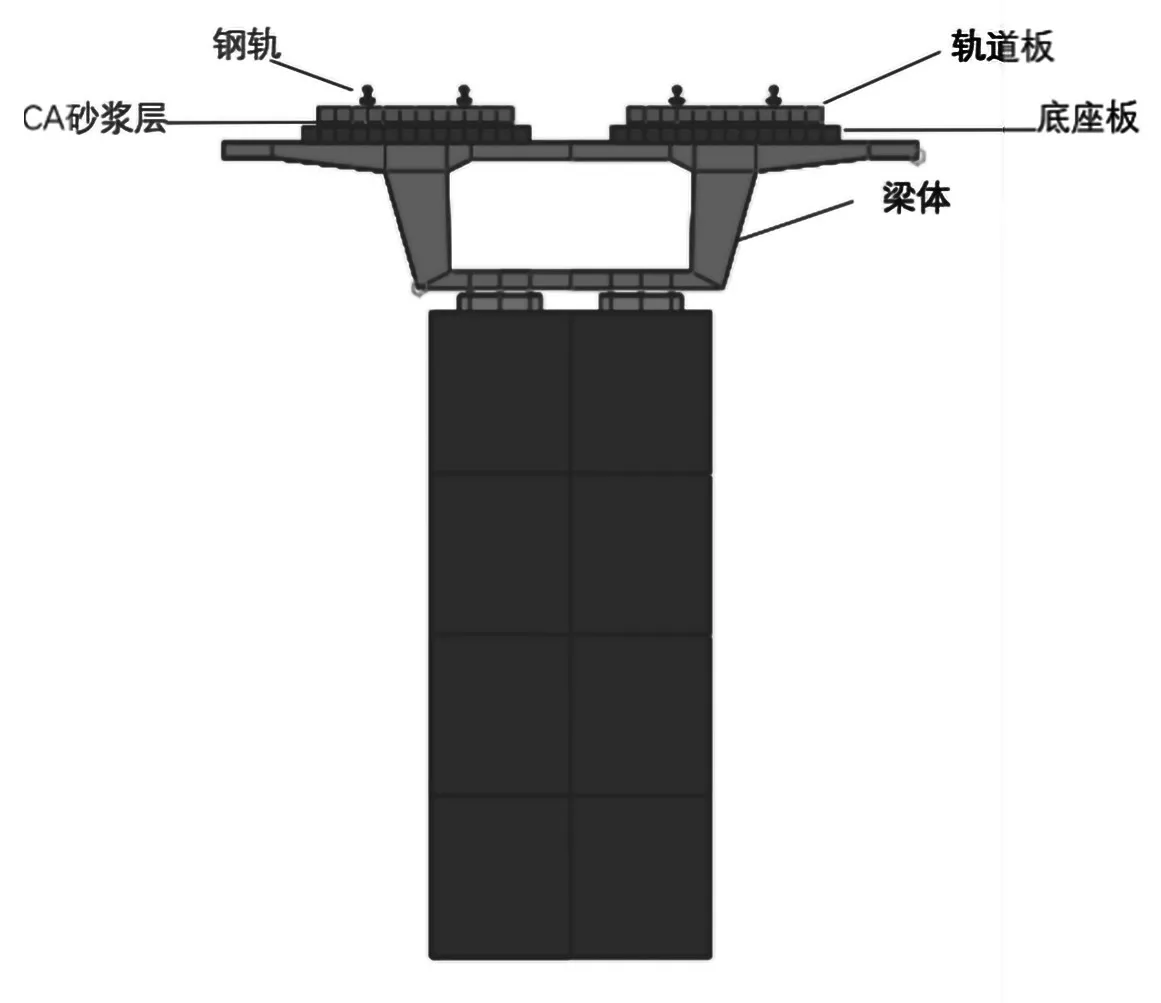
图2 模型横断面图

模型参数取值，如表1 所示。

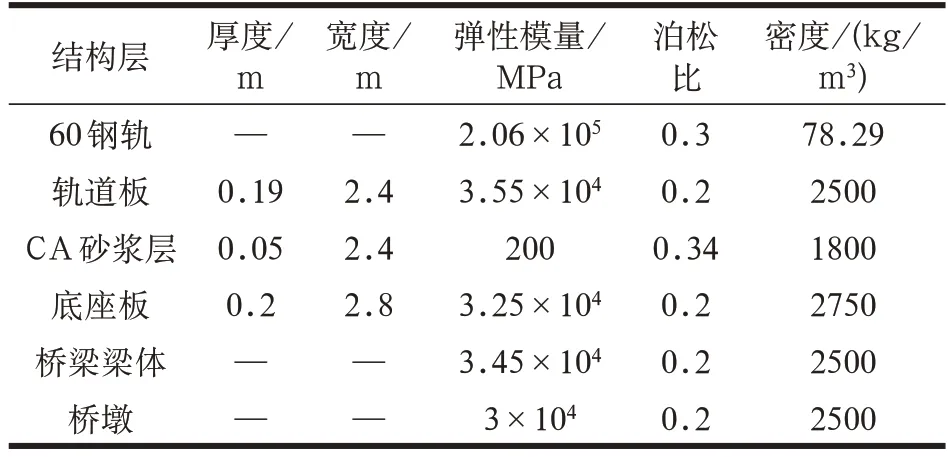
表1 板式无砟轨道—桥梁模型参数取值

1.2 荷载工况

工后不均匀沉降按照两种工况考虑：一是按照其中某一个桥墩发生沉降位移，其他桥墩不发生沉降位移；二是所有桥墩均发生沉降位移但存在沉降差。根据有关规范规定，对于桥上无砟轨道，其墩台均匀沉降位移不大于30mm，不均匀沉降位移不大于15mm，沉降差不大于15mm；10m 弦长的轨道高低不平顺幅值不大于2mm。因此，选取8 种工况进行计算，并比较计算结果，如表2 所示。所有工况均为4 跨桥梁5根桥墩的中间桥墩发生沉降。

表2 桥墩沉降量 单位：mm

2 计算结果分析

2.1 桥墩沉降幅值对无砟轨道平顺性的影响

针对高速铁路线路中多跨简支梁桥桥墩沉降对钢轨轨面几何条件的影响问题，本文按表2 荷载工况进行对比，研究当桥墩沉降量不同时，钢轨变形趋势、最值以及区域长度等。

2.1.1 轨道结构计算结果分析

利用纵连板式无砟轨道与桥梁有限元模型，计算了当桥墩沉降量不同时，轨道结构的钢轨以及轨道板随之变化的变形曲线，如图3、图4 所示。

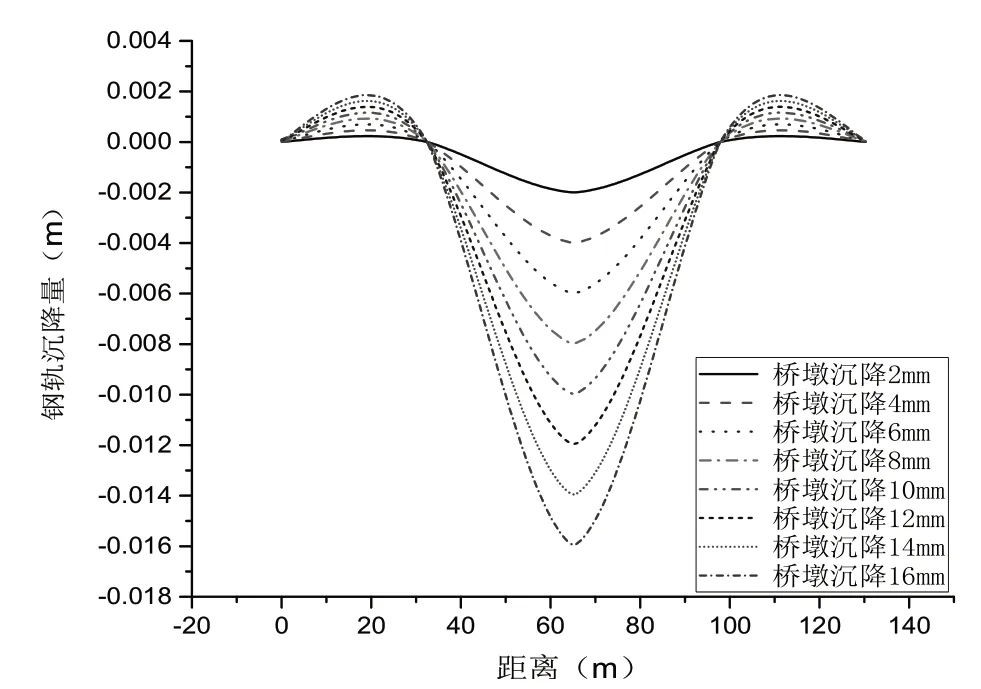
图3 钢轨整体变形图

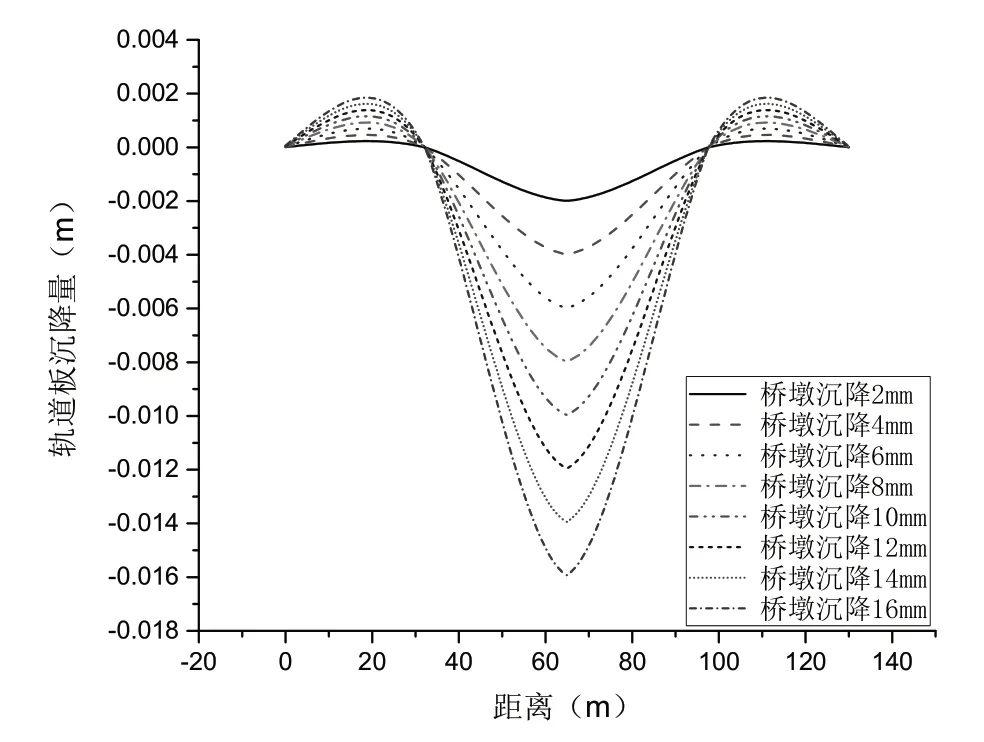
图4 轨道板整体变形图

由计算结果可知，桥墩下沉对相邻两跨梁影响最大，与梁相连的轨道板随桥墩沉降而沉降，钢轨、轨道板、CA 砂浆层、底座板在自身重力作用下下沉，因为CRTSⅡ型板是纵连结构，轨道结构变形协调。针对桥上铺设纵连板式轨道的情况，当桥墩发生沉降时，钢轨亦会随之发生变形，在进出沉降作用区域时钢轨略微上翘，到达沉降墩节点处时有缓和过渡曲线。而在远离沉降作用区域时钢轨变形量急速衰减。当桥墩发生不同沉降量时，钢轨变形趋势均保持一致。随着桥墩沉降量的增加，钢轨的变形量包括上翘和下沉的幅度都在增加。在进出沉降作用区域时钢轨上翘现象明显，形成的“拱形”越明显；在远离沉降作用区域时钢轨变形急速衰减，不受桥墩沉降量变化的影响。轨道板与钢轨变形趋势均保持一致，仅在量值上有所区别。

桥墩取不同沉降量时无砟轨道结构及梁体的最大下沉位移，如表3 所示。由表3 可以看出，桥墩取不同沉降量时，轨道结构最大沉降量随桥墩沉降量的增加而增加，轨道结构自下而上沉降量最大值呈逐渐减小的趋势，钢轨沉降量最小，底座板沉降量最大。箱梁沉降量大于轨道底座板沉降，并且随桥墩沉降量增加而增加。钢轨下沉量与桥墩沉降量之间差异不大，因为轨道板、CA 砂浆层和底座板为混凝土结构，刚度较大，板间连续性较好，故与桥墩沉降同幅度。

表3 轨道结构及梁体最大沉降量 单位：mm

桥墩取不同沉降量时无砟轨道结构及梁体的最上拱量如下表4 所示。

4）训练方式、手段及步骤：将学生分成几个小组（5人一组），每个小组确定说话的类型，小组内进行谈论，要求每位学生都参与，说话时间至少3分钟；小组训练结束后，教师在随机抽取各小组几名学生，进行即兴说话，学生和老师按照既定标准进行的评分和点评。

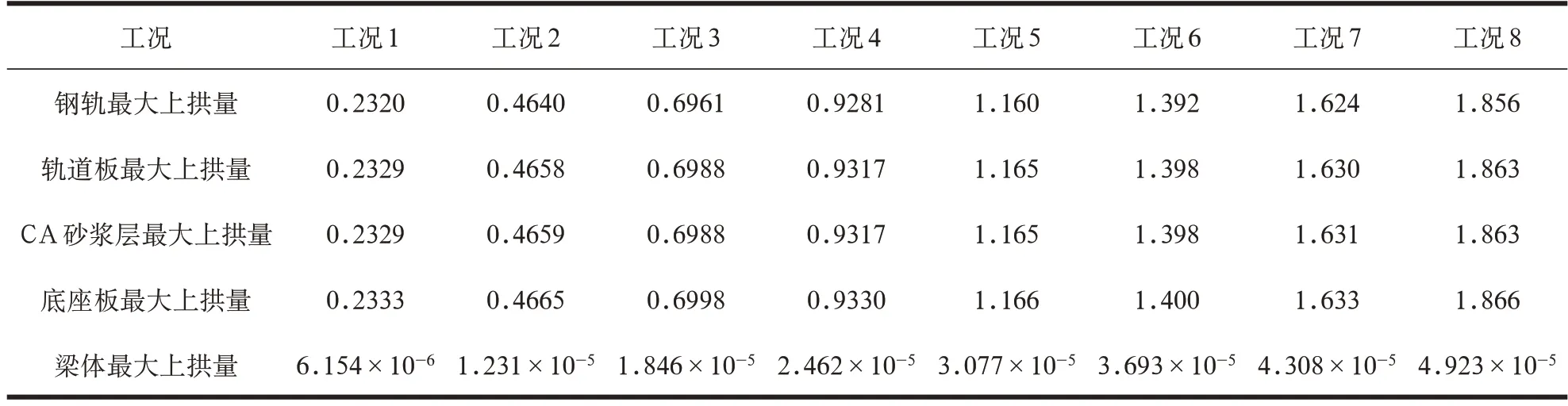
表4 轨道结构及梁体最大上拱量 单位：mm

由表4 可以看出，桥墩取不同沉降量时，轨道结构最大，上拱量随桥墩沉降量的增加而增加；轨道结构自下而上，上拱量最大值呈逐渐减小的趋势；钢轨上拱量最小，底座板上拱量最大；箱梁上拱量随桥墩沉降量增加而增加，但量值很小。

2.1.2 钢轨变形最值曲线拟合

当桥墩发生不同沉降量时，钢轨向下、上变形最大值，如图5 所示。

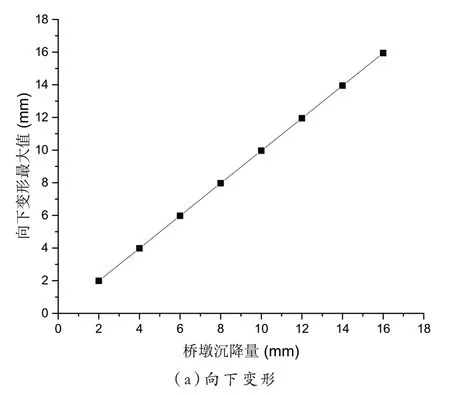
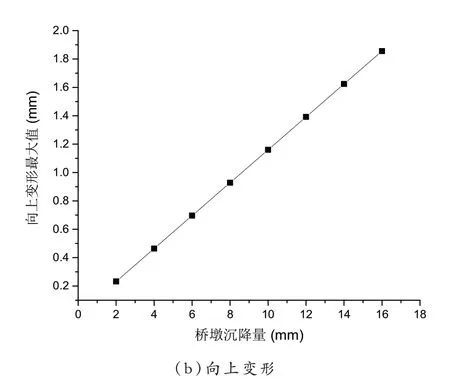
图5 钢轨变形最值与桥墩沉降量关系图

由图5 可知，钢轨变形最值均随桥墩沉降量的增加呈线性变化。采用线性拟合公式对桥墩沉降量和钢轨向下变形最大值进行拟合，最终得到的公式为：

式（1）中：相关系数r2=1（r 值的绝对值介于0～1 之间。通常来说，r 越接近1，表示x 与y 两个量之间的相关程度就越强，反之，r 越接近于0，x 与y 两个量之间的相关程度就越弱）；采用线性拟合公式对桥墩沉降量和钢轨向上变形最大值进行拟合，最终得到的公式为y=0.116x+0.00005，相关系数r2=1。

2.1.3 钢轨变形区域

表5 桥墩沉降引起的钢轨变形区域长度

钢轨变形延伸系数随桥墩沉降量的变化，如图6所示。

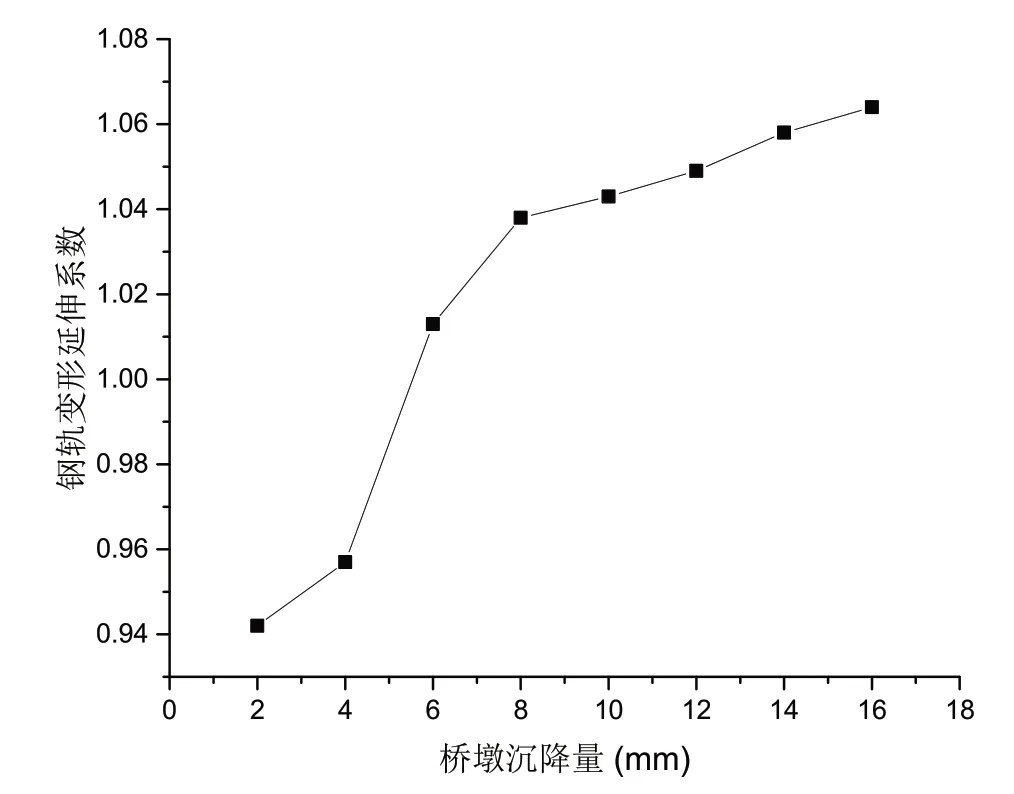
图6 钢轨变形延伸系数随桥墩沉降量的变化图

由分析可见，钢轨变形区域长度及钢轨变形延伸系数随桥墩沉降量增加而增加。当桥墩沉降量较小且一般小于5mm 时，由于无砟轨道各部件结构的变形互相作用及钢轨本身竖向抗弯刚度的作用影响，钢轨变形区域长度小于梁体变形区域长度，此时钢轨变形延伸系数小于1；当桥墩沉降量较大时，钢轨变形区域长度大于梁体变形区域长度，此时钢轨变形延伸系数大于1。总结来说，当桥墩沉降值在2～16mm 范围时，钢轨变形延伸系数会随着桥墩沉降量的增加，在开始作用阶段增长较快，后作用阶段增长逐渐缓慢。桥墩沉降值为2mm 时，钢轨变形延伸系数最小为0.942，当桥墩沉降值为16mm 时，钢轨变形延伸系数最大为1.064。

2.2 桥梁跨度对无砟轨道平顺性影响

为进一步研究桥梁跨度对无砟轨道平顺性影响，基于桥梁—轨道变形映射模型，研究高速铁路不同跨度简支梁桥和CRTSⅡ型板式无砟轨道结构，分析高速铁路桥梁跨度分别为24m 和32m 时的钢轨变形区域长度和钢轨变形最值等，分析两种不同桥梁跨度对轨面几何条件映射程度的影响规律。

取桥墩沉降6mm、12mm 为例，相同桥墩沉降量下桥梁跨度对轨面几何条件的影响，如表6 所示。

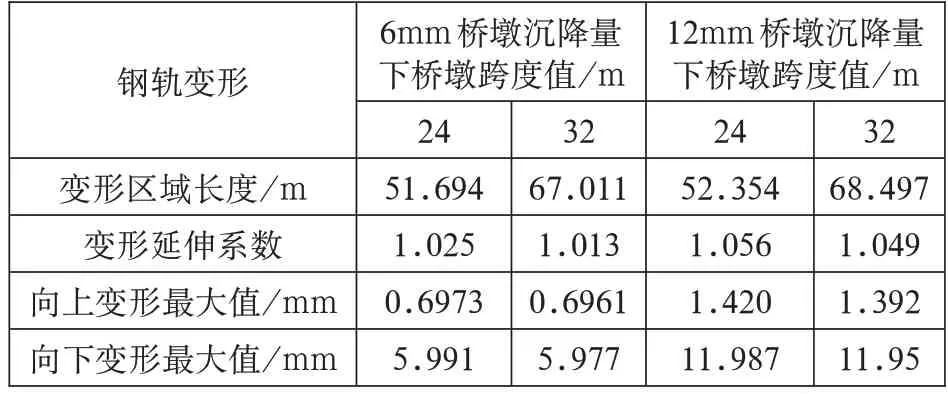
表6 不同桥梁跨度时钢轨变形数据对比表

由表6 可知，当桥墩沉降量一样时，钢轨变形区域长度随桥梁跨度增加而增大，钢轨变形延伸系数随桥梁跨度增加而减小。桥墩沉降作用下钢轨变形最值随桥梁跨度增大而减小。这是由于随着桥梁跨度的增大，桥梁变形越平缓，钢轨的变形曲线亦趋于缓和，由沉降导致的轨面附加不平顺波长变长，该不平顺对轨面激励的影响越小。

3 结论

本文研究了桥墩沉降作用下的无砟轨道结构的平顺性，建立了纵连板式轨道—桥梁结构有限元模型，从桥墩沉降幅值、桥梁跨度两个角度，得到了以下结论：

其一，对于桥上纵连板式轨道，桥墩发生沉降，轨道结构也会随之发生变形，随着桥墩沉降量的增加，轨道结构最大沉降量、上拱量随桥墩沉降量的增加而增加；轨道结构自下而上沉降量、上拱量最大值均呈逐渐减小的趋势，钢轨沉降量、上拱量最小，底座板最大。

其二，在进出沉降作用区域时，钢轨略微上翘，到达桥梁沉降墩节点处时有缓和过渡曲线。桥墩发生不同沉降量时，钢轨变形趋势相同；随着桥墩沉降量的增加，钢轨的上翘“拱形”越明显、下沉的幅度增大。在远离沉降作用区域时钢轨变形急速衰减，基本不受桥墩发生沉降量的影响。钢轨变形最值，包括向下和向上变形最大值，均因桥墩沉降量增加呈线性变化，线性拟合公式分别为y=0.9963x-0.0008（r2=1）、y=0.116x+0.00005，（r2=1）。

其三，随着桥墩沉降量的增加，钢轨变形区域长度及钢轨变形延伸系数呈现增加的趋势，开始增长较快，后增长逐渐缓慢。当桥墩沉降量较小且一般小于5mm，钢轨变形延伸系数小于1；当桥墩沉降量较大时，钢轨变形区域长度大于梁体变形区域长度，钢轨变形延伸系数大于1。

其四，相同桥墩沉降量下，随着桥梁跨度的增加，钢轨变形区域长度增大，但钢轨变形延伸系数减小。随着桥梁跨度的增大，桥梁变形越平缓，钢轨的变形曲线亦趋于缓和，由沉降导致的轨面附加不平顺波长变长，该不平顺对轨面激励的影响越小。