上覆黏土层条件下考虑空间变异的砂土地基地震液化可靠度研究

陈 胜,周旭辉,吴勇信

(1.江苏省岩土工程公司,江苏 南京 210019; 2.河海大学土木与交通学院,江苏 南京 210098)

岩土工程的地震响应分析得到了越来越多学者的关注[1-4]。砂土地基的地震响应是一个重要的工程问题。地震作用下,饱和砂土趋于密实,土体表现出孔隙水压力升高的特性。由于地震作用时间短,这种急剧上升的孔隙水压力来不及消散,导致土颗粒间的有效应力突然降低,进而使土体的抗剪强度降低,影响了地基的稳定性[5]。2008年中国汶川地震就明显发现由于地震液化导致地基和结构发生严重破坏的现象。这些破坏引起人们对防治土体液化的广泛关注,不少学者利用室内模型试验和数值模拟对其进行了研究。董瑞等[6]针对含弱渗透性覆盖层的饱和砂土地基进行离心机振动台试验,并采用OpenSees软件对试验模型进行数值模拟。蔡正银等[7]通过离心机振动台试验研究了深埋砂层地基的动力反应和液化规律。许成顺等[8]进行了可液化自由场在水平地震动激励下的大型振动台模型试验,分析了饱和砂土液化后场地加速度、位移等动力响应。Zhuang等[9]利用商业有限元软件分析了现有地铁结构在液化土中的相互作用效应及其附近的液化响应。张艳美等[10]采用FLAC3D软件分析一致激励、局部液化和行波激励对隧道结构动力响应的影响。Ali等[11]采用FLAC2D程序进行数值模拟,研究了土体类型、结构重量和液化土层厚度对地震反应的影响。Chen等[12]通过数值模拟研究了3种典型的土剖面对地下结构的影响,发现地下结构穿过液化层时会对结构的地震响应产生不利影响。

上述不同研究中土的性质和荷载特性都是以某个确定的数值表示,而在工程实践中,结构周围土体与地震荷载具有随机性和空间变异性。Miao等[13-14]从地震荷载的空间变异性对隧道的不同响应进行了分析;Wu等[15-17]在不同土工设计概率方法数值分析中分别引入土体的空间变异性和不确定性,明确指出考虑土体空间变异特性的重要性。目前对于土体地震液化空间变化规律的研究方面,Popescu等[18]将非线性有限元分析与蒙特卡罗模拟和非高斯向量场结合,研究了土体参数的空间变异性对土体液化的影响,发现在相同地震荷载的作用下,考虑土体参数空间变异性的土体会比同等条件下的均质土体在地震发生时累积更多的孔隙水压力;Lopez-Caballero等[19]评估了土壤参数对砂土地震反应的随机性,发现随机模型的相关长度明显地决定了液化概率。

土体空间变异性对土体液化有显著影响,但大多数学者对砂土地基地震响应还是基于均质土体的假设进行计算分析,忽略了土体的成层性及空间变异性,这与实际情况不符,并且可能在一定程度上低估了工程问题的危险性[20-22]。本文基于土体空间变异性对地震诱发土体液化的影响等问题进行数值研究,采用结合蒙特卡罗模拟的有限差分法来评估液化区面积、超孔隙水压力和地表位移,比较了不同空间相关非高斯随机场的随机模型对土体剪切模量的模拟结果,分析了土体剪切模量变异系数对上覆黏土层砂土地基地震动力响应的影响。

1 剪切模量随机场模拟方法

剪切模量随机场模拟主要步骤为:首先生成一个空间相关随机场的样本函数来表示分析区域内剪切模量的分布,生成特定的土体参数,随后将其导入有限差分程序,并进行动态响应分析,在一系列蒙特卡洛模拟之后,最终得到土体液化响应规律。

选用谱表现法[23-24]并通过MATLAB程序模拟各向异性空间相关的剪切模量非高斯随机场,谱表现法在随机场模拟上表现出良好的特性,并用二维相关函数来描述剪切模量在空间中的相关性:

(1)

式中:τx、τz分别为空间任意两点在水平和竖直方向的滞后距离;δx、δz分别为在水平和竖直方向的波动范围,波动范围是描述土体参数在空间中相关性大小的参数。

(2)

其中κxli=l1iΔκx(l1i=0,1,…,N1-1)

κzli=l2iΔκz(l2i=0,1,…,N2-1)

Δκx=κxu/N1Δκz=κzu/N2

式中:Δκx、Δκz分别为频率坐标轴上κx和κz的离散区间;κxli、κzli分别为对应方向的截断频率;φl1l2为两个相互独立的随机变量序列,其满足(0,2π]之间的均匀分布;SG(κx,κz)为目标高斯功率谱函数;ξx、ξz分别为水平和竖直方向上的坐标值;N1、N2分别为沿水平和竖直方向离散功率谱密度函数的点数;κxu、κzu分别为相应的上截止波数;ρG为相关函数。对于式(1)定义的互相关函数,其对应的功率谱密度函数为

(3)

(4)

Wu等[24]提出一种具有较高计算效率和收敛速度的样本迭代方式,可得到潜在高斯概率密度函数。当确定了潜在高斯概率密度函数SG(κx,κz),通过式(2)即可得到标准潜在高斯随机向量场,由式(4)可映射得到标准非高斯随机向量场。

2 数值模型与参数

2.1 计算模型

采用有限差分软件FLAC3D建立二维平面应变模型,对存在5m厚的上覆层黏土及地下水位1m以下砂土层在地震荷载作用下的液化反应进行非线性动力学模拟。砂土层动力液化分析范围在水平(x)、竖直(z)、纵深(y)方向分别为40m、10m、1m的矩形区域。模型在y方向划分为一个单元格来模拟平面应变情况。下部9m厚的饱和可液化砂土层上部覆盖了1m厚的干砂层,即地下水水位位于地表下1m处,而在干砂层上部增加了厚度为5m的黏土层。本文土体均采用实体单元模拟,网格划分均为1m×0.5m的矩形网格,有限差分模型共1200个网格,3层土层从上到下分别为400个、80个、720个单元格,有限差分数值模型示意图如图1所示。

图1 黏土-砂土液化地基数值模型示意图

2.2 土体参数

土体参数参考试验所得[25],采用Mohr-Coulomb模型来模拟土体非线性性状,可液化土层采用Finn模型模拟,该模型能够模拟土体在动荷载作用下孔隙水压力的累积直至液化的过程。Finn模型的基础是摩尔-库伦模型,但是增加了动孔压的上升模式[26]。

剪切强度满足空间非高斯随机场的特征,其均值为20MPa,土体的确定性分析中土体本构模型力学参数的取值如表1所示。

表1 土体数值计算模型参数取值

2.3 动力荷载和边界条件

本文计算偏向规律性研究,采用较高的抗震设防烈度为标准,选用设防烈度为8度的El-Centro波作为输入波源,将峰值加速度为0.3g、持时为30s的El-Centro波加速度水平分量(图2)施加于模型底部。

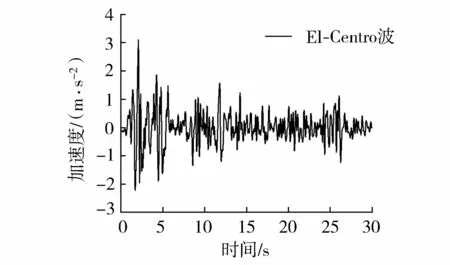
图2 El-Centro加速度时程曲线

在静力计算过程中,土体仅受重力作用的静力平衡计算需要固定模型并控制边界位移才有意义,因此对模型底部所有方向的位移及侧边x、y方向的位移进行约束。而在动力计算过程中,边界被用来吸收反射的地震波和模拟数值模型的离散半空间条件,因此静力分析中的边界不再适用,故通过在侧边施加自由场边界来减少模型边界波的反射。此时模型底部解除约束以施加地震波。

基于上述数值模型和参数取值,赋予砂土层符合Lognormal分布、水平波动范围和竖向波动范围均为6m的空间变异剪切模量随机场,对每种情况生成200种随机场工况进行黏土-砂土地基的地震动力液化可靠度分析,用不同的变异系数(C= 0.1、0.3、0.5)评价剪切模量变异系数对液化响应的影响。饱和土在动力激励作用下的显著特征包括孔隙水压力的累积、内应力的降低和失稳。选用液化区域面积A80(t)和液化指数Q(z,t)两个指标进行分析。A80(t)为发生液化区域的大小与砂土分析区域大小之比,可表示为

(5)

Q(z,t)为高差z和t时刻的超孔隙水压力比的平均值,按水平方向平均超孔隙水压力计算:

(6)

式中:x、z分别为元素在水平方向和垂直方向的中心坐标;n为水平方向元素的个数。

3 计算结果与分析

3.1 上覆黏土层对液化范围的影响

图3为不同剪切模量变异系数下液化范围A80时程曲线。在地震作用过程中,可以观察到4个不同阶段:在0～6s处于液化区生长期阶段;6～8s处于液化区还原期阶段;8～20s处于液化区震荡期阶段;20～30s处于液化区消散期阶段,几乎没有发现反弹现象。

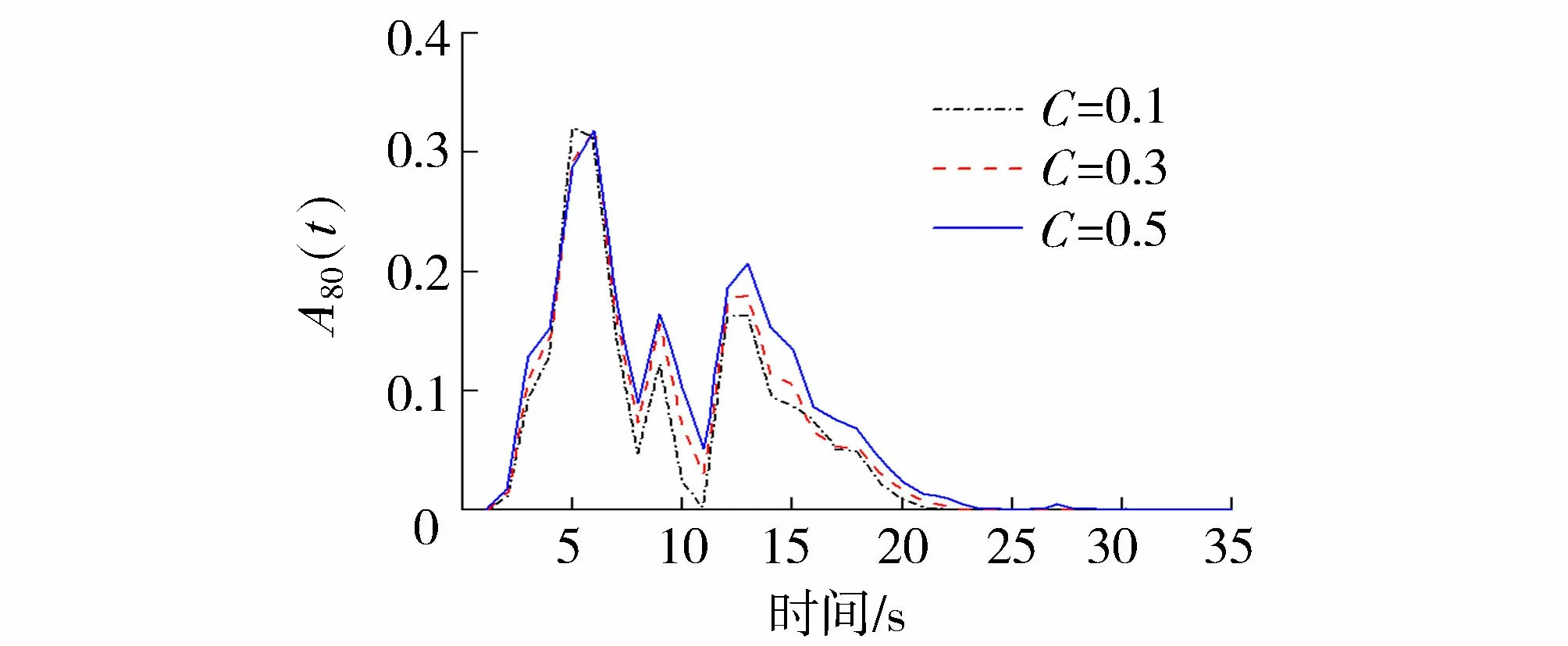
图3 不同变异系数下黏土-砂土地基液化范围时程曲线

由图3可以看出,在液化区还原期,液化范围缩小的速率随剪切模量变异系数的增大而逐渐减小,并且在液化范围震荡期的残余液化面积大小也随剪切模量变异系数的增大而增大,即剪切模量变异系数的增大会使得液化范围缩小越困难。

图4为黏土-砂土地基的液化范围峰值概率分布(PDF)曲线,由图4可见,随着砂土剪切模量变异系数的增大,液化范围峰值的分布范围越分散,且PDF曲线的峰度越小。

图4 不同变异系数下黏土-砂土地基的液化范围峰值概率分布曲线

3.2 上覆黏土层对超孔隙水压力比的影响

由于大量孔隙水压力持续累积在砂土层7.25m深度,图5为黏土-砂土地基地表下12.25m埋深处(即砂土层下7.25m埋深处)的平均超孔隙水压力比Q(t)时程曲线。超孔隙水压力比因地震荷载的作用,累积上升速率随剪切模量变异系数的增大而逐渐减小,超孔隙水压力消散速率(即Q(t)时程曲线下降的斜直线段斜率)随剪切模量变异系数的增大而减小,这与液化范围缩小速率随变异系数的变化规律相对应。此外,也可观察到超孔隙水压力比因地震荷载瞬时增强而出现较小程度的反弹增大,但并未随变异系数不同而表现出明显的规律。

图5 地表下12.25m埋深处超孔隙水压力比均值时程曲线

3.3 上覆黏土层对地表位移的影响

地表位移是地表结构稳定性的重要指标。为了研究上覆黏土条件下黏土-砂土地基地表位移情况,提取不同变异系数下200次随机性工况的地表(即黏土层表面)水平位移、沉降和差异沉降。

图6为不同剪切模量变异系数的地表水平位移均值和标准差时程曲线,可以看出下部砂土存在于上覆土层,其地表水平位移随砂土剪切模量变异系数的增大而增大,且地表水平位移的标准差也随剪切模量变异系数的增大而增大,表明剪切模量变异系数越大,地表水平位移越大且离散程度越大。

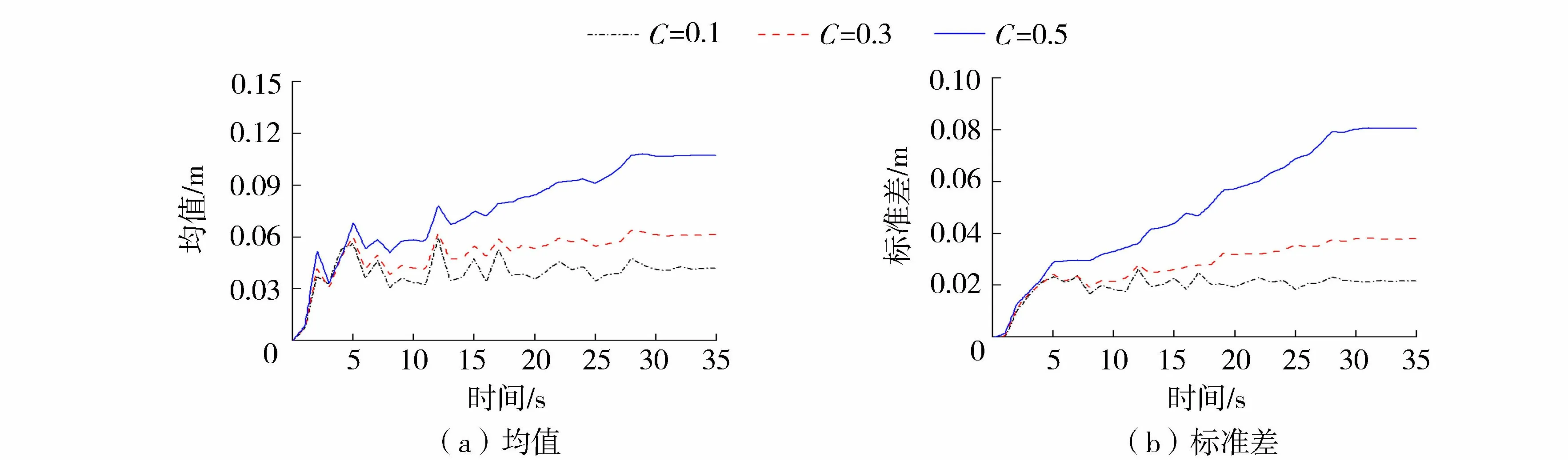
图6 不同变异系数下地表水平位移均值和标准差时程曲线

提取计算时间内黏土-砂土地基地表沉降最大值,绘制地表最大沉降的累计概率分布(CDF)曲线,如图7(图中黑、红、蓝色柱状图和实曲线分别代表砂土C=0.1、0.3、0.5时的地表最大沉降累计分布及其拟合的累计概率分布曲线;黑色竖直实线表示使用砂土剪切模量随机场均值进行确定性分析得到的地表最大沉降值,黑、红、蓝色竖直虚线分别代表不同剪切模量变异系数下随机分析得到的最大沉降均值)所示。由图7可见,黏土-砂土地基的地表最大沉降分布范围随剪切模量变异系数的增大而逐渐广泛,且最大沉降均值随剪切模量变异系数的增大而增大。此外,均质确定性工况不能全面描述非均质砂土的液化位移特性,当C=0.1、0.3、0.5时,200组随机工况中分别有33.5%、35.4%、38.2%的工况预测地表位移大于确定性均质工况的地表位移。

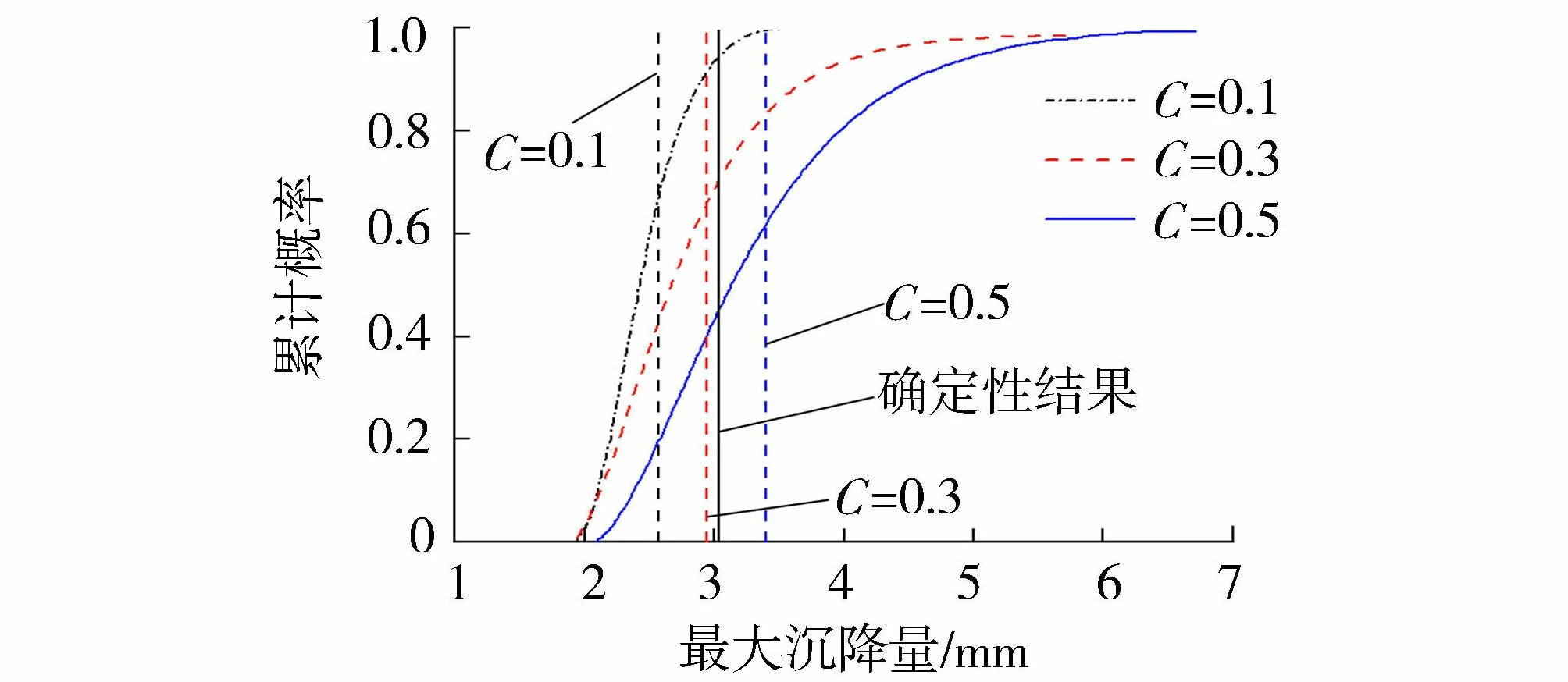
图7 地表最大沉降的累计概率分布曲线

图8为黏土-砂土地基地表最大差异沉降的概率分布(PDF)曲线图。地表最大差异沉降是指地震发生后,地表处各个时刻发生的最大和最小沉降差值的最大值。由图8可知,对比不同砂土剪切模量变异系数随机场计算得到的地表差异沉降,可以发现地表最大差异沉降随剪切模量变异系数的增大而增大,且其随机结果的分散程度也随变异系数的增大而增大。

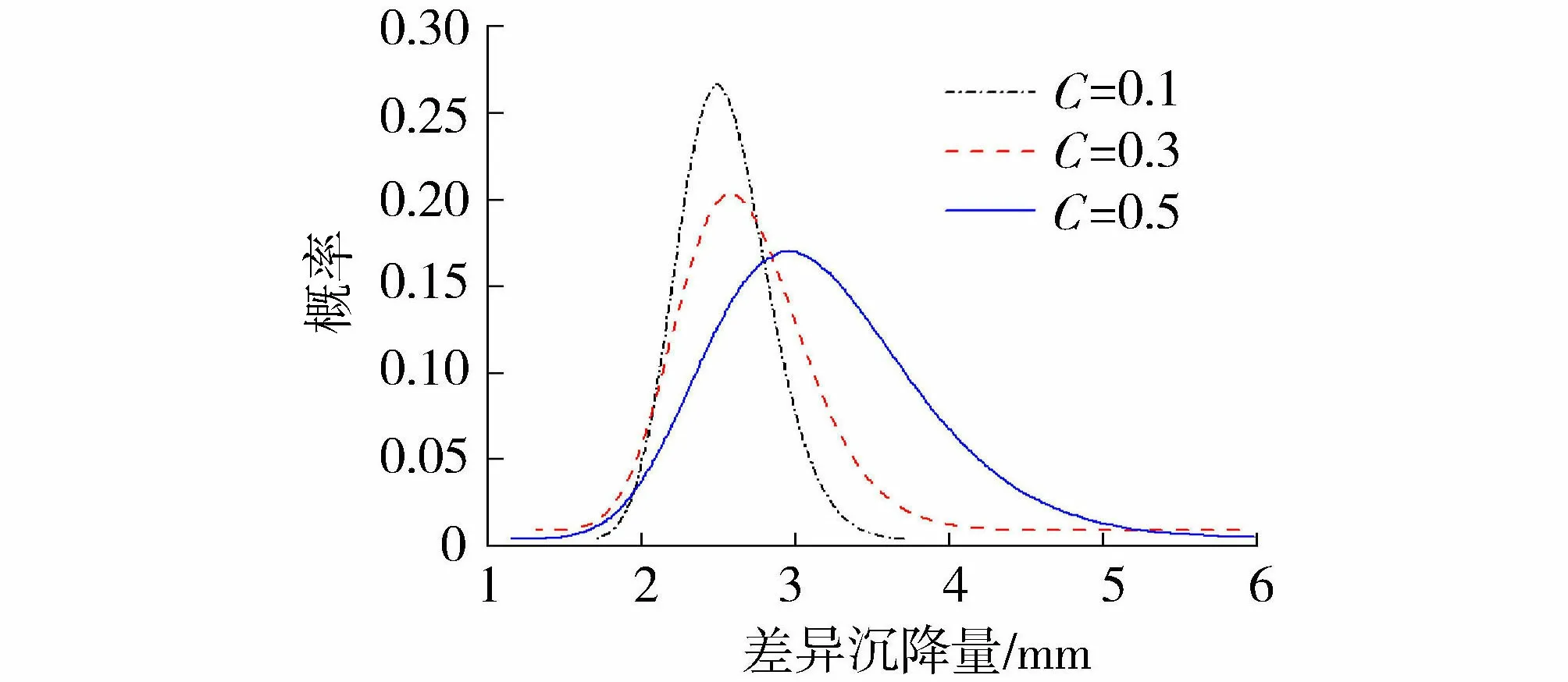
图8 地表最大差异沉降概率分布曲线

4 结 论

a.剪切模量变异系数对黏土-砂土地基在地震荷载下发生液化引起的液化范围、超孔隙水压力比和地表位移有一定的影响,即剪切模量变异系数越大,液化范围缩小越困难,液化范围峰值分布越分散,孔隙水压力消散越慢,地表水平位移越大且分布越广泛。

b.从液化地基地表位移的角度而言,地表最大沉降分布范围随剪切模量变异系数的增大而逐渐广泛,且最大沉降均值随剪切模量变异系数的增大而增大;地表最大差异沉降也随剪切模量变异系数的增大而增大。

c.剪切模量变异系数C=0.1、0.3、0.5时,随机工况的地表位移分别有33.5%、35.4%和38.2%的概率大于确定性均质工况的地表位移,表明在分析砂土地基的地震响应时有必要考虑土体空间变异性。