含水率波动状态下公明公路路基土劣化微观机理与本构模型

李立宇,陈远中,徐思远

(1.深圳市公明供水调蓄工程管理处,广东 深圳 518107;2.南京水利科学研究院岩土工程研究所,江苏 南京 210024; 3.河海大学水利水电学院,江苏 南京 210098)

通常情况下道路工程中的土体会在其最优含水率附近进行压实,并保证相对压实度不低于95%。但研究表明,路基土服役期间其含水率会逐渐上升至最优含水率湿侧,且随着气候的变化其含水率在最优含水率湿侧某一区间内波动[1-2]。含水率变化和波动往往会对路基土的物理力学性质造成影响,进而影响道路的正常使用。

国内外学者开展了大量试验研究含水率变化对土体力学特性的影响。研究表明,随着初始含水率的升高,土体黏聚力和内摩擦角均会急剧减小[3-4],但有些学者得出黏聚力在最优含水率附近存在峰值,内摩擦角在最优含水率干侧随着含水率的增大而减小,在最优含水率湿侧变化不明显,说明含水率对土体强度参数的影响与土体自身的物理性质有关[5];在应力-应变关系方面,随着含水率的增加,土体的应力-应变曲线由应变软化型向应变硬化型转变,试样的破坏形式逐渐由脆性破坏转为塑性破坏[6]。含水率波动对土体力学特性影响的研究成果还相对较少。干湿循环作用对土体力学特性的影响,实际上可以看作是一种含水率波动的影响,但是干湿循环一般在极端的气候条件下发生,因此可以认为干湿循环是一种程度剧烈的含水率波动情况[7]。但是,目前还没有关于含水率波动程度对路基土微观结构和力学特性劣化规律的研究。

本文设定3种不同程度的含水率波动,通过固结排水三轴剪切试验,研究含水率波动程度对深圳市公明公路路基土力学特性的影响,并结合微观试验结果探究含水率波动状态下路基土力学特性的劣化微观机理,最后基于邓肯-张模型,建立了考虑含水率波动影响的路基土经验本构模型。

1 试验方案

1.1 试样制备

对从深圳市公明水库4号坝体所在地区附近所取的公路路基土进行去除腐化植物和石块,然后将其风干、研磨过2mm筛去除大颗粒,依据GBT50123—2019《土工试验方法标准》测得其塑限为16.2%,液限为30.9%,相对密度为2.69,最优含水率为14.3%,最大干密度为1.86g/cm3。颗粒分析试验测得土体试样中砂粒占52.4%,粉粒占23.7%,黏粒占23.9%。试样在最优含水率及最大干密度下分3层采用重型静力压实成直径为38mm,高度为76mm的圆柱形试样,每层压实后用土工刀在其表面拉毛,保证层间不会发生断层现象。试样制备完后立即从模具中推出,用保鲜膜包裹后放置于密封盒中静置24h达到水分平衡再开展后续试验。

1.2 静三轴试验

杨树荣等[1]通过对137处服务中的道路路基进行现场调查,指出全部59处黏性土的现场含水率皆位于最优含水率wopt湿侧(其余78处为颗粒土),主要在wopt～wopt+7%之间波动;Uzan[2]发现,黏性路基土在最优含水率下压实后,含水率会随着气候条件的波动,在最优含水率湿侧某一区间内波动。为了探究含水率波动程度对路基土力学特性的影响,本文拟定了3种不同程度的含水率波动状态:零波动状态(wopt,称为OMC状态)、弱波动状态(wopt～wopt+1.2%,称为OMC-TMC状态)和强波动状态(wopt～wopt+2.3%,称为OMC-SMC状态)。参考Han等[8]提出的湿制试样方式,使用不同干湿程度的滤纸包裹OMC状态下的试样直至质量达到目标含水率下的质量,即认为试样增湿至目标含水率,随后在自然条件下脱湿至最优含水率,完成1次含水率波动。研究表明,在经历5～7次干湿循环后试样的基本力学特性会达到稳定[9-10],因此本文中含水率波动次数设定为10次,以研究最终平衡下路基土试样的力学特性。

含水率波动处理之后的试样进行三轴固结排水试验前,先对试样进行真空抽气饱和,并在去离子水中浸泡24h,随后将试样转移到三轴压力室内进行反压饱和,当孔隙水压力系数超过0.98即认为试样达到饱和状态[11]。围压为100kPa、200kPa、300kPa和400kPa下的饱和试样固结完成后,以0.076mm/min的速率对其进行剪切,在轴向应变达到15%时停止剪切。

1.3 微观试验

对经历3种不同程度含水率波动达到最终平衡状态下的试样开展压汞(MIP)试验和扫描电镜(SEM)试验,研究土体微观结构的演化机制。其中MIP试验用于测定试样的孔径分布曲线,SEM试验用于捕捉试样的微观结构图像[12-14]。在进行MIP和SEM试验之前采用冻干法[15]对试样进行了干燥处理,具体过程为:将制备好的试样直接放入液氮中,使内部水分在-196℃的低温下快速冻结成冰,然后通过真空抽气的方法使土体内的冰晶直接升华为水蒸气,从而在去除土体内水分的同时最大程度地保留试样原始的微观结构。

2 三轴试验结果与分析

由图1可知,围压σc较低时试样的偏应力-轴向应变关系表现为应变软化型,随着围压的增加开始转变为应变硬化型,应力峰值强度所对应的轴向应变随围压的增加而增大。围压较低时,试样的体应变随着轴向应变的发展先增加而后减小为负值,表明试样在剪切过程中先经历剪缩后发生剪胀,试样的剪胀特性随着围压的增加而减小,当围压较高时其体应变随轴向应变的发展逐渐增加并趋于稳定,试样仅表现为剪缩特性。

图1 OMC状态下三轴固结排水试验结果

对比图2(a)和图3(a)可以看出,OMC-TMC状态下试样仅在σc= 100kPa时表现出应变软化;试样经历含水率弱波动(OMC-TMC)后,σc= 200kPa和σc= 300kPa条件下其应力-应变关系均转变成应变硬化型;试样在经历含水率强波动(OMC-SMC)后,所有围压下试样的应力-应变关系均表现出应变硬化型。对比图2(b)和图3(b)可以看出,含水率波动使得试样在剪切过程中剪缩特性表现更为明显,且含水率波动程度越大,试样的剪缩特性越明显。

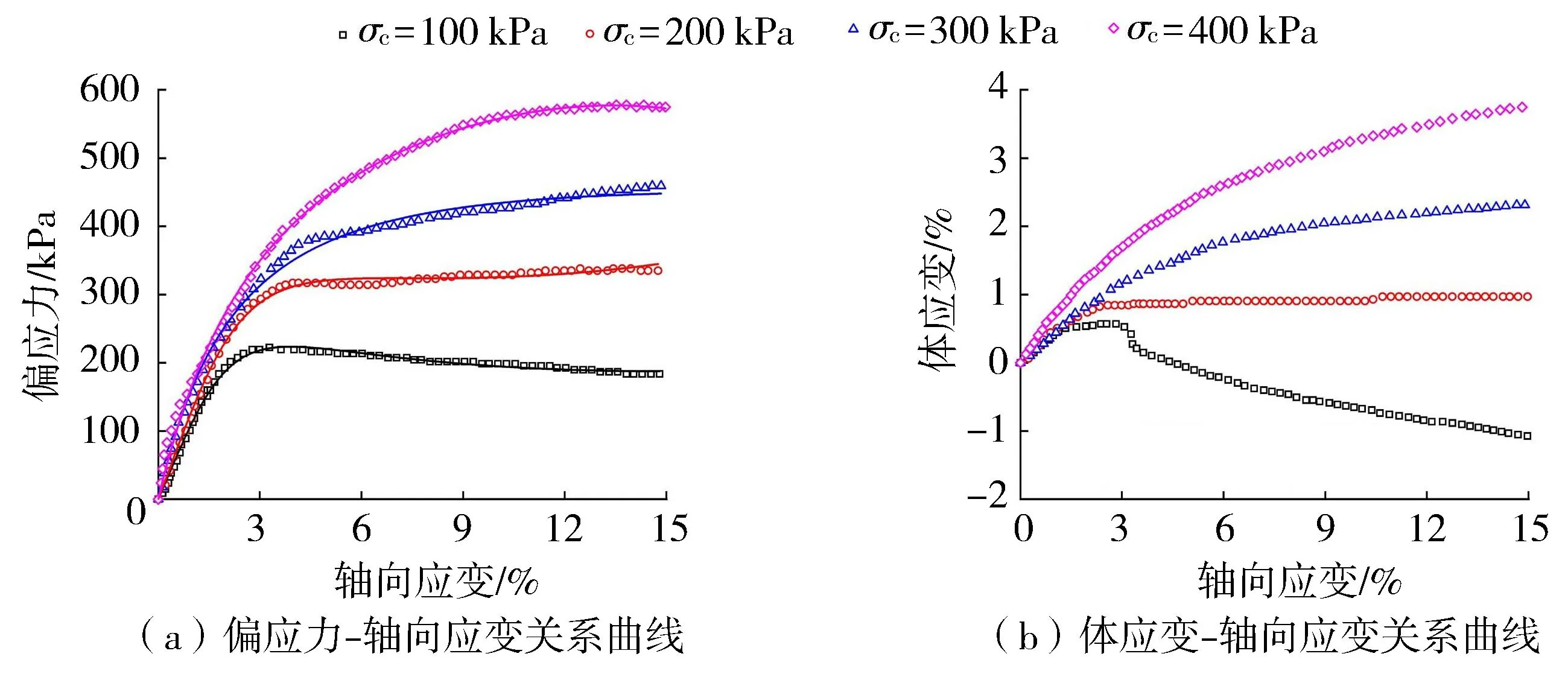
图2 OMC-TMC状态下三轴固结排水试验结果

图3 OMC-SMC状态下三轴固结排水试验结果

取应变软化型的偏应力-轴向应变曲线峰值偏应力作为试样破坏时的偏应力,取应变硬化型的应力-应变曲线15%轴向应变处的偏应力作为试样破坏时的偏应力,对试样在固结排水三轴试验破坏时的应力进行分析,试样应力莫尔圆如图4所示。从图4可以看出,经历3种不同程度的含水率波动后,土体试样仍符合Mohr-Coulomb抗剪强度理论。由表1可知,含水率波动导致试样黏聚力和内摩擦角均有所减小,说明含水率波动会降低试样的剪切强度,这与文献中干湿循环降低土体强度参数的结论一致[7,16]。

表1 土体剪切强度指标

3 微观试验结果与分析

3.1 MIP试验

综合已有文献中的孔隙划分经验[17-18],按孔径尺寸d将孔隙划分为:微孔隙(d≤0.1μm)、小孔隙(0.1μm30.0μm)。从图5可以看出,OMC状态下试样的孔隙结构为单峰结构,峰值位于2μm左右,小孔隙占比较大,中孔隙占比较小。经历含水率波动后,孔径分布曲线逐渐由单峰模式向双峰模式转变,2μm处孔径分布曲线的峰值逐渐下移并在中孔隙的孔径范围内出现了一个新的峰值孔径。

图5 试样的孔径分布曲线

由表2可知,随着含水率波动范围的增大,试样的孔隙分布表现出不同的发展趋势:微孔隙基本保持不变,其数量和尺寸仅与试样内部的黏土矿物有关,因此不受含水率波动的影响;小孔隙数量逐渐减少,由于在波动过程中不断经历脱湿和增湿作用,小孔隙产生的塑性收缩变形会导致体积减小,波动范围越大这种塑性收缩越显著;中孔隙和大孔隙数量增多,表明水分的迁移会引发试样内部大、中孔隙的发育。土体中、大孔隙的产生,是引发土体剪缩特性明显的主要原因。根据孔隙均匀化原理[19],试样受剪切后大孔隙优先改变,从而使得试样内部孔隙趋于均匀,这种大孔隙的均匀化在宏观上就表现为体缩。由于含水率波动程度越大,水分迁移过程中所产生的大孔隙比率越大,大孔隙的均匀化在整个剪切过程中就越显著,其剪缩特性就越明显。

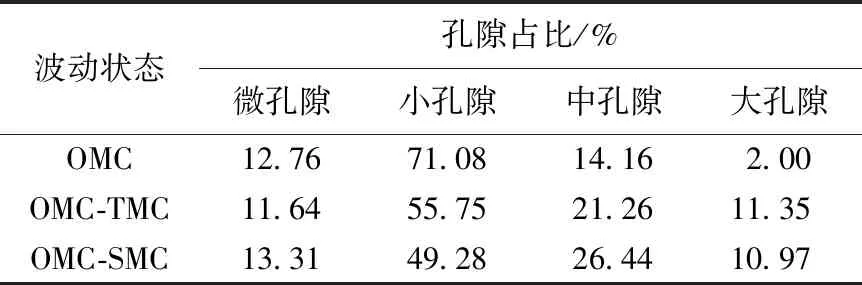
表2 各级孔隙占比

从表2还可以看出,尽管含水率波动会促进试样内部各级孔隙占比的调整,但含水率波动范围对孔隙占比的调整影响不大,表中OMC-TMC与OMC-SMC状态下各级孔隙占比的变化幅度都不及OMC与OMC-TMC状态下的变化幅度明显。意味着只要发生含水率波动,不论波动范围的大小,试样的微观结构都会受到较大的影响,因此在实际工程中含水率波动对路基土力学特性的影响不可忽视。

3.2 SEM试验

图6(a)为OMC状态下试样400倍镜的SEM图像,可以看出试样观测断面平整细腻,整体结构均匀,视域内多见小孔隙,偶见细小裂缝,裂缝间贯通性差,试样内部存在微小缺陷。由图6(b)(c)可以看出,含水率波动影响后试样观测断面参差不齐且菱角分明,整体结构差异性大。试样孔隙及土体结构变化明显,微裂隙在数量、宽度和长度上均有不同程度的增加。裂隙将试样分割为块,块体间接触多为“面-面”接触,块体内小孔隙数量大幅下降,与MIP试验所得含水率波动后试样小孔隙峰值下降的结果相一致。含水率波动过程中微裂隙发展导致的土体结构变化,是导致土体试样抗剪强度减小的主要原因。

图6 试样的SEM图像(放大400倍 )

4 经验本构模型

对于较高围压下试样的应变稳定和硬化行为,可以采用邓肯-张模型进行描述[20],表达式为

(1)

式中:σd为偏应力;εa为轴向应变;a、b为模型拟合参数,其中1/a为极限偏应力,其值等于试样的排水抗剪强度,1/b为应力-应变曲线的初始斜率,其值等于试样的初始弹性模量。

由于较低围压下试样的应力-应变关系表现为应变软化型(图1、图2),邓肯-张模型并不能很好地描述软化行为,因此在邓肯-张模型的基础上,提出了一个经验本构模型(式(2))用于对本文不同含水率波动状态后试样的应力-应变关系进行描述。

(2)

式中m、n为模型拟合参数。m与应力-应变曲线出现软化的拐点相关,曲线越早表现出软化现象m越小;n与试样的软化程度相关,试样的软化程度越高n越大,当n= 1时,式(2)与邓肯-张模型的表达式一致。因此,式(2)既可以描述应变软化行为,也可以描述应变稳定和硬化行为。

式(2)对不同含水率波动状态后试样应力-应变曲线的拟合效果分别如图1(a)、2(a)、3(a)所示,模型参数见表3,可以看到模型的拟合R2均大于0.99,说明了该模型拟合能力的稳定性与可靠性。

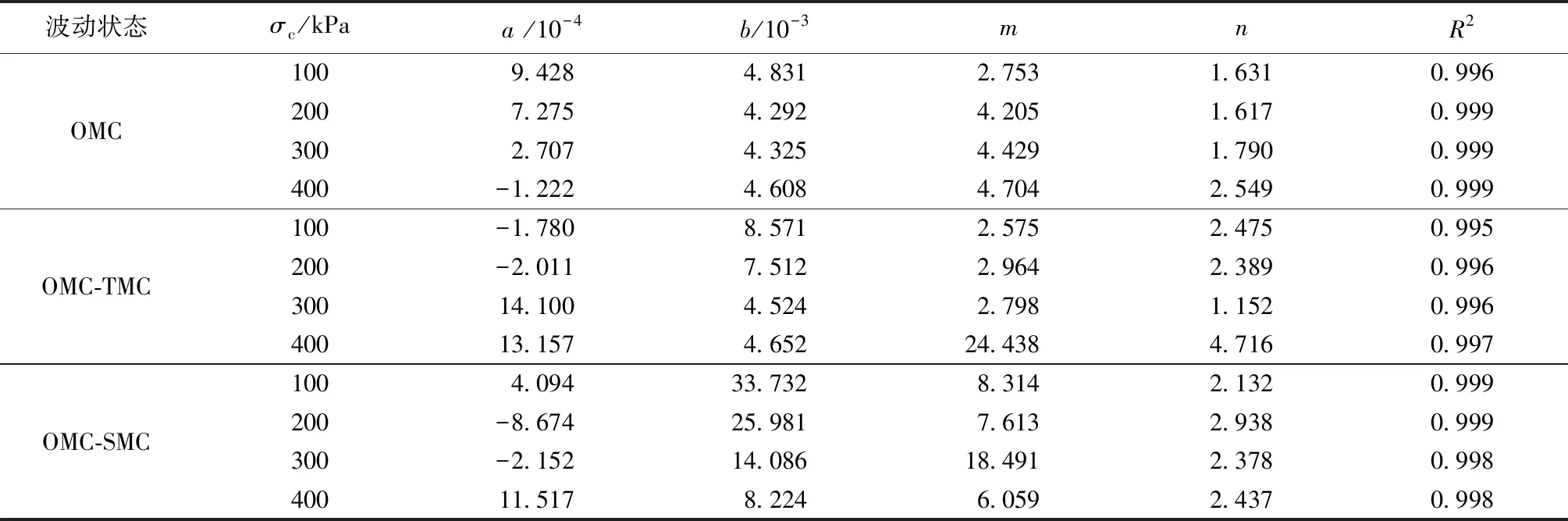
表3 经验本构模型参数值

5 结 论

a.含水率波动过程中水分迁移引发试样内部产生的大孔隙增多,导致路基土试样剪切应力-应变关系从应变软化向应变硬化型转变,试样剪缩特性提升,随着含水率波动程度的增大,试样的剪缩特性越明显。

b.含水率波动过程中微裂隙得到发展,微裂隙的发展导致试样结构有所破坏,从而降低了试样黏聚力和内摩擦角,随着含水率波动程度的增大,试样剪切强度越小。

c.基于邓肯-张模型提出了一个经验本构模型,既可以用来描述试样的应变软化行为,也可以用来描述应变稳定和硬化行为,较好的拟合结果证明了该模型的有效性和适用性。