水文水力学结合的秦淮河流域洪水模拟与实时校正

汪昊燃,王 容,黄鹏年,何 健,姚 成

(1.河海大学水文与水资源学院,江苏 南京 210098; 2.水利部水文水资源监测预报中心,北京 100053;3.南京信息工程大学水文与水资源工程学院,江苏 南京 210044; 4.江苏省水文水资源勘测局,江苏 南京 210029)

中小河流流域的洪水预报一直是防汛工作的重点[1-3]。分布式水文模型如栅格新安江模型等,对山地丘陵地形时空模拟精细化程度较高,在汇流阶段一般采用马斯京根法或扩散波计算汇流,计算结果受河道地形、回水顶托和闸坝建筑等影响,导致模拟精度降低[4-11]。水力学模型对感潮河段潮位计算具有良好的模拟精度,但上游山地丘陵地区多为天然河道,地形复杂,断面形状不规则,造成水力学相关参数计算困难[12],因此有必要将水文学模型与水力学模型相结合,以此来建立河流与流域之间的水力联系。殷骏[13]在南四湖区对水文和一维水力耦合预报模型的研究明确了该模型的可行性和稳定性;在水文学和水力学模型结合的基础上,李致家等[14]对比了一维水力学模型和二维水力学模型的适用情况,发现一维水力学模型计算精度在低水位情况下受各水体之间连通性影响较大;孙映宏等[15]根据山区、平原区、分洪区以及河道等不同的产汇流条件将水文学与水力学模型耦合后应用在山前小流域,取得了良好的模拟效果。一维水力学模型在低水位计算时,由于各水体之间水流交换减少,导致模拟结果精度受到影响,需采用实时校正方法对误差结果进行修正[16]。实时校正方法一般分为过程误差校正方法和终端误差校正方法,在一维水力学模型的实时校正中,可采用卡尔曼滤波法对区间入流、状态变量等过程进行校正[17-19],也可采用K最近邻(K-nearest neighbor,KNN)法等对计算结果进行校正。KNN法[20]不需要建立自回归方程,不需要计算相关参数,在实时校正中有较好的应用前景[21]。刘开磊等[22]采用KNN法对一维水力学模型计算结果进行校正,发现该方法能较大程度、稳定地提高模拟精度;反馈模拟法对于较短的预见期有良好的校正效果,且与预报模型无关,同样是终端误差实时校正的常用方法之一[23]。

秦淮河流域河网密集,上游以山区为主,坡度较大;下游河段出口与长江相连,其水位受长江潮汐作用影响显著,属于感潮河段且同时受水闸调度的影响。本文采用栅格新安江模型与一维河网水力学模型结合的模型模拟水位。在流域上游山地丘陵地区采用栅格新安江模型计算出流,流域下游平原感潮河段采用一维水力学模型计算水位,并对计算结果实时校正,以期提高洪水水位模拟的精度。

1 研究区域概况

秦淮河流域位于长江下游,地形四周高、中间低,坡度较大,总面积2684km2;上游属山地丘陵区,下游地区河道窄、坡度小的地形条件导致流域上游汇流快,下游泄洪缓慢[24]。

东山站位于南京市江宁区东山大桥上游200m处,是秦淮河流域下游出口的水位控制站。秦淮河在东山站下游300m处分流入老秦淮河及秦淮新河。秦淮新河全长16.8km,秦淮新河闸位于秦淮新河河口处;武定门闸位于老秦淮河中段,与东山站相距12km,见图1。武定门闸上水位站、秦淮新河闸上水位站主要为调度作用,东山站为主要负责报汛的水位控制站,因此选取东山站作为水位模拟计算的研究水位站。东山站水位受到上游来水、武定门闸、秦淮新河闸以及长江潮汐的影响,汛期水位上涨迅速,因此水位呈现绳套或非单一性复杂关系。

2 预报模型构建

2.1 栅格新安江模型

栅格新安江模型产流部分采用蓄满产流模型,计算单元栅格冠层截留量、河道降水量以及蒸散发量以推求地表径流、壤中流和地下径流,再将3种水源按各栅格间的演算次序演算至流域出口;模型汇流部分采用主网格马斯京根法,将3种产流水源依次演算至站点出口[25]。整理2010—2018年东山站逐时水位资料,2014—2018年秦淮河流域的逐日降雨、径流资料,以秦淮河水系上游前垾村(秦)站为水文模型及水力学模型的分界点,流域上游采用栅格新安江模型进行模拟。DEM网格大小为1km×1km,流域内共有9座水库,出流均按主网格马斯京根法演算至前垾村(秦)站;前垾村上游包含11个雨量站,均在流域范围内。

2.2 水力学模型

秦淮河干流采用一维河网水力学模型进行计算。模型的上边界采用由栅格新安江模型计算的流量过程,以流域下游出口处的长江潮位作为河网水力学模型的下边界。

前垾村(秦)站下游包括秦淮新河闸上、武定门闸上、东山站3个水位站,云台山河、牛首山河和外港河3条主要支流;秦淮河干流在东山站分为人工河道秦淮新河和老秦淮河两条河流汇入长江(图2)。前垾村(秦)站至下游出口共设有86个断面,其中秦淮新河糙率取0.022,老秦淮河糙率取0.024,其余支流糙率取0.021。秦淮新河闸与武定门闸为调度水闸,调度规则均为当水位低于6.5m时引水,当水位高于8.5m时泄洪。前垾村(秦)站以下流域地势低洼,存在多个圩区,将圩区分为水面、水稻田、旱荒地和城市道路进行计算;产流计算将土壤分为两层,采用蓄满产流方法计算;圩区内采用单位线法计算汇流,汇流至圩区河道后,以圩区排涝模数进行量化,作为旁侧入流进入秦淮河河道内。

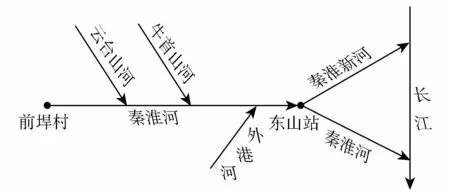
图2 河网概化图

采用的河网水力学方程为圣维南方程组:

(1)

(2)

式中:A为过水断面面积;Q为流量;u为流速;Z为断面水位;g为重力加速度;S0为水流沿程损失;Sf为摩阻比降。将式(1)用四点线性Preissmann隐式格式进行差分,可以得到任一河段差分方程:

(3)

式中Cj、Dj、Ej、Fj、Gj、φj均为系数,由初值计算。

河网水力学模型将河网分为树状河网和环状河网。前垾村(秦)站至东山站之间的河道及汇入河道的支流呈树状河网水系,采用树状河网追赶法进行河道水位计算,即对于已知的流量边界条件,上断面L1和下断面L2可假设如下追赶关系:

(4)

式中:j为断面编号(j=L1,L1+1,L1+2,…,L2-1);K、T、P、V为追赶系数。由式(2)和式(3)联立可得递推关系,依次求得Kj+1、Tj+1、Pj+1、Vj+1,最后得到:

QL2=PL2-VL2ZL2

(5)

式(5)与下边界条件QL2=f(ZL2)联解可得ZL2,依次回代可求得Zj、Qj。

环状河网包括内河道和外河道,外河道计算与树状河网计算类似,均由河道一端边界条件已知的外节点推求另一端水力要素未知的内节点。东山站以下的老秦淮河、秦淮新河构成环状河网水系,采用环状河网双追赶系数法进行水位计算。内河道的计算没有端点边界条件可用,河段差分方程依然可表示为式(2),首、末断面水位为基本未知量,因此需要利用双追赶方程求解。

3 实时校正方法

3.1 KNN法

KNN法校对计算主要包括4个步骤:①计算模拟时段前70%的误差数据存放为全部历史误差数据,用于以后时段的实时校正;②根据误差自回归理论,考虑前面多个时段(NT),设定预见期为ext,则可以从NT+ext时刻开始至m-1+NT+ext建立m个历史预报误差向量集;③识别最近邻样本,以向量间的欧式距离为评价相似相关性的指标,找出与当前预报误差相关向量最相似的X个预报误差向量;④对该X个预报误差向量对应的预报误差加权,使用反距离权重法对当前误差进行估计。

3.2 反馈法

反馈法基于洪水预报误差的相似性,对洪水预报误差进行实时校正,在洪水预报实时校正方面已取得较好的结果[26]。反馈法通过计算实测流量与预报流量之间的反馈因子(F),将流量过程分为涨洪段和落洪段,进而对预报流量进行修正。

先从第2个时刻起计算各时刻与前一时刻的流量差:

ΔQobs,i=Qobs,i-Qobs,i-1

(6)

ΔQcal,i=Qcal,i-Qcal,i-1

(7)

式中:Qobs,i为本时刻实测流量;Qcal,i为本时刻预报流量。

通过各时刻与前一时刻的预报流量差和实测流量差,计算F:

(8)

可以得到涨水段反馈模拟实时校正计算公式为

Qobs,i=Qobs,i-1+ΔQcal,iF

(9)

退水段反馈模拟实时校正计算公式为

(10)

4 计算结果对比

选取秦淮河流域2014—2018年9场典型洪水,采用栅格新安江模型计算前垾村(秦)站上游至该站的产汇流过程,选定前8场进行次洪模型参数率定,最后1场用来检验。部分分布参数由输入的土壤类型、植被覆盖类型等数据直接计算,如自由水蓄水容量SM、张力水蓄水容量WM等。部分敏感参数率定结果为:蒸散发折算系数1.00;上层张力水容量占比0.17;下层张力水容量占比0.50;地下水消退系数0.993;壤中流消退系数0.90;河网水流消退系数0.83。洪水模拟结果如表1所示。

表1 前垾村(秦)站洪水模拟成果统计

根据GB/T 22482—2008《水文情报预报规范》:模拟计算结果中,前垾村(秦)站以上流域8场洪水,径流深合格率与洪峰合格率均为87.5%;预报检验的1场洪水径流深和洪峰都合格。所选9场洪水的径流深误差与洪峰误差都达到乙等精度要求。由栅格新安江模型计算的前垾村(秦)站洪水流量过程可用于一维水力学模型上边界流量输入过程。

选取次洪模拟中的5场洪水进行水位模拟计算。将前垾村(秦)站的模拟流量过程作为一维水力学模型上边界流量输入条件,下游出口处长江潮位作为一维水力学模型的下边界,并采用KNN法和反馈法进行实时校正。对模拟水位的评价标准主要考虑其与实测水位的绝对误差,因此对东山站水位计算结果的评价采用确定性系数(CNSE)和洪峰水位误差(δPE)2种指标。对未校正的栅格新安江-河网水力学模型计算成果、反馈模拟法校正的计算成果和KNN法校正的计算成果分别计算两种指标,计算结果如图3所示。部分模拟水位过程如图4所示。

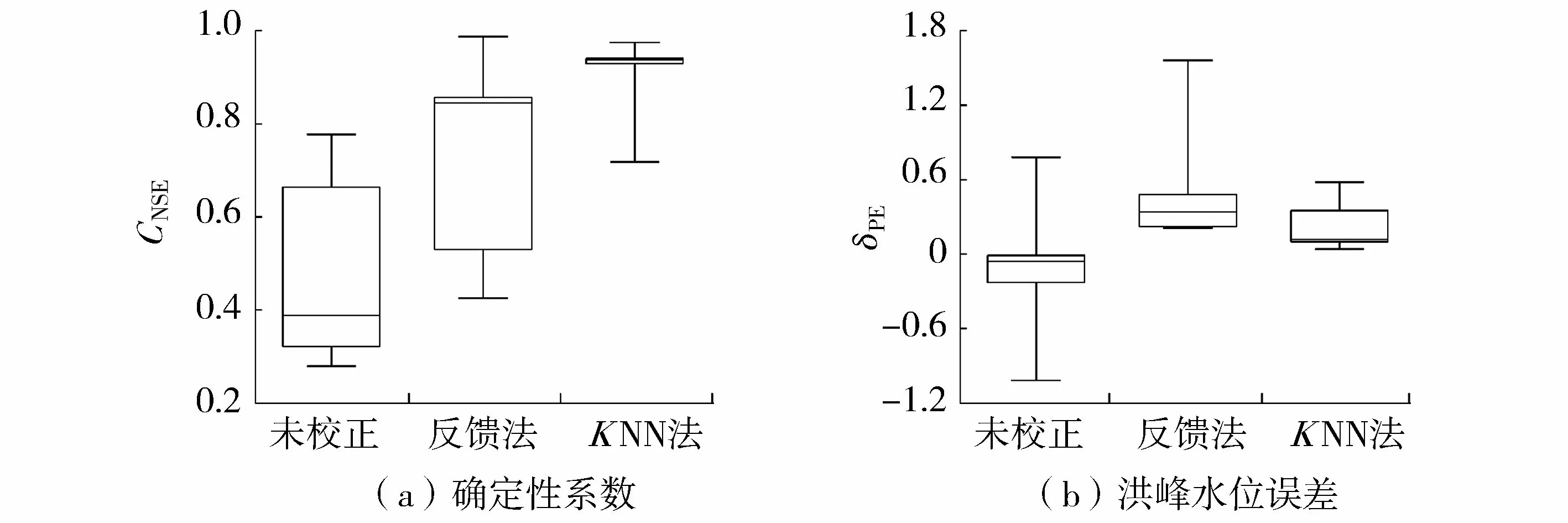
图3 校正方法指标对比

图4 模拟水位过程

由图3中可以看出:未校正的水位模拟计算结果存在较大的不确定性,经过反馈法和KNN法校正后的模拟水位过程确定性系数均有较大提升,且KNN法校正效果相比反馈法更好。对于洪峰水位绝对误差,未校正的模拟洪峰水位计算结果波动较大,经过校正后精度得到提高,且KNN法校正后的模拟洪峰水位误差更加稳定,误差值在0.04～0.55m之间,模拟精度较高。2015062508号洪水未校正的模拟水位确定性系数为0.388,该场洪水的上边界前垾村(秦)站的入流模拟结果较好,但经过河网水力学模型计算后,东山站的模拟水位较实测水位相差较大,造成确定性系数偏小。经过调查,本场洪水在南京市区造成严重内涝,因此在三汊河口处人工开凿临时泄洪道,对下边界条件产生影响,导致高水位时模拟结果与实测结果误差较大。同时根据调度规则,下游两处水位站会在水位高于8.5m时泄洪,因此模拟水位在8.5m左右时会出现模拟调度实际未调度或模拟未调度实际调度的情况,造成在低水位时模拟结果不佳。经过实时校正后,2015062508号洪水洪峰/水位模拟结果和确定性系数均大幅度提高,可以满足模拟精度要求。

2017060920号洪水未校正的模拟水位误差只有0.13m,但确定性系数仅为0.322。同时根据水位过程线可知,由于模拟的水位过程涨水阶段相较于实测水位过程滞后约12 h,造成确定性系数偏小。分析前垾村(秦)站入流情况可知,在洪水发生初始阶段该站流量为负值,即出现逆流情况,而栅格新安江模型模拟流量过程不会出现逆流情况,因此上边界条件出现较大误差,造成模拟水位过程与实际水位过程在时间尺度出现偏移。经过KNN法校正后的水位模拟过程在最高水位时出现了一些精度损失,而峰现时差以及确定性系数有了较大的提高。

在实时校正前,栅格新安江模型与河网水力学模型结合的预报方法对水位的模拟计算结果受平原圩区地形影响较大,且因模型的局限性导致在低水位时模拟结果不佳,洪峰水位模拟精度较高但峰现时间有较大误差。而对模拟结果采用KNN法和反馈法进行实时校正后,均能有效提高东山站水位模拟精度。对比2种实时校正方法,反馈法计算简单,KNN法可以根据实际预报需要灵活调整参数,且校正后的水位模拟结果相较于反馈法精度更高。

5 结 语

秦淮河流域地势四周高中间低,形成了许多圩区,导致上游汇流快,下游泄洪慢,且受水闸泵站和长江潮汐的影响,洪水预报工作具有不确定性和复杂性。本文构建以栅格新安江模型计算的前垾村(秦)站流量过程为一维河网水力学模型上边界、以下游出口处长江潮位为模型下边界的水位模拟计算模型,选取秦淮河流域2014—2017年的5场次洪水进行水位模拟计算。结果表明,河网水力学模型对平原圩区河道汇流计算具有较高的精度,结合栅格新安江模型的预报径流过程作为上边界输入条件后,实现了对受水工建筑物影响的感潮河段水位的模拟计算。在经过实时校正之后,解决了低水位情况下水位预报精度不高的问题,其中KNN法校正后确定性系数为0.718～0.975,达到了乙等预报精度要求,可为秦淮河流域防汛提供参考。由于本文所选洪水场次较少,还需要在收集更多资料后对该模型进行进一步计算验证和校正,逐步形成预报可靠性较高的秦淮河流域栅格新安江与河网水力学结合的预报模型。