基于“逆向设计”的声学超材料几何参数容差设计*

钟林君 杨 扬 舒乐时

（1.华中科技大学机械科学与工程学院数字制造装备与技术国家重点实验室 武汉 430074）（2.华中农业大学工学院 武汉 430070）

1 引言

声学超材料由于能够实现对任意频率声波及弹性波的有效控制，具有传统材料无法替代的性质，在声探测、声通信、声隐身等方面都有重要的应用价值［1］。声学超材料波控器件通常由大量微结构构成，量化微观结构的尺寸与声波响应的关系以确定允许的加工误差范围，是能否制备出满足需求的材料的关键与难点。MILTON等［2］率先提出的五模材料（Pentamode Material，PM）是一种新型的人工声学超材料。随后，聚合物基五模材料［3～4］与金属基五模材料［5～6］陆续研制成功，因金属基五模材料与流体的力学性能相似，在水声控制领域被广泛接受。

常见的二维五模材料均为蜂窝结构，可通过对单胞角点施加不同质量的配重块来调整超材料对波的响应特性，而如何量化单胞各尺寸参数与微结构性能之间的关系是五模材料制备过程中的难点。ZHAO 等［7］同时考虑力学与声学性能，设计了一种类水五模材料微结构；HAN［8］等提出蜂窝-波纹混合的轻质夹层结构，并研究其压缩性能，为五模材料的结构设计提供新思路。但上述研究对五模材料结构参数与性能之间的关系还没有非常清晰的量化［9］，同时微结构的加工精度与缺陷均影响着制备出的声学器件的性能。此外，现有的五模材料主要通过水枪切割、线切割及微细加工制备，其中，微细加工精度最高，但成本大；线切割技术加工精度次之，而切割厚度大；水枪切割加工精度最低。因此，为保障加工不确定性下的声学超材料的性能，需要平衡制备成本与产品性能之间的关系，提供合理的允许加工误差。

日本学者TAGUCHI 博士20 世纪70 年代提出了三次设计法［10］，其中容差设计是在参数设计完成后，综合考虑产品质量和成本的情况下确定设计参数的容差值，并提出以质量损失函数为目标的容差优化模型［11］。由于稳健性分析能够有效保障不确定性环境下的产品质量，越来越多的容差设计结合稳健性分析方法应用于实际的工程问题［12～13］。采用稳健性分析的方法，可以在加工不确定性下保证微结构性能变动在可接受的范围内。然而，现有的基于非概率理论的稳健性分析方法大多属于“正向模型”，即通过将变量的变化映射到目标空间和可行性空间来验证最优解的稳健性［14］。当修改输入变量的不确定信息时，基于正向模型的方法需要重新分析设计方案的稳健性［15］。同时，在许多复杂工程产品的设计中，设计目标和约束的非线性与隐式程度较高，难以直接得到参数变化与质量损失及成本的关系。采用基于“逆向设计”思维的稳健性分析方法，可通过将目标可接受变化范围（Acceptable Objective Variations Region，AOVR）及约束可接受变化范围（Acceptable Constraint Variations Region，ACVR）映射至参数空间，建立不确定性参数与目标及约束的关系，从而获得不确定性参数的容差范围。

对此，本文提出基于“逆向设计”思维的稳健性分析方法，并对声学超材料的几何参数进行容差设计，获取不确定性参数的最大容差范围。

2 “逆向设计”思维

通常，考虑区间不确定性的设计优化问题可以描述为

其中，设计优化问题包括M 个目标与G 个约束，f为第m个目标函数，g表示第i个约束条件，xL、xU为变量x 的设计范围，且x的区间不确定性变化Δx被限制在上下边界ΔxU、ΔxL内变动。

基于“逆向设计”模型，可以将给定的AOVR 及ACVR 映射至变量变化区域，进而在不确定性变量空间进行稳健性分析。其中，AOVR 可以表述为[Δf-，Δf+]，如图1 所示；ACVR 由所有起作用的约束组成：gi(x+Δx)≤0，i=1，…，G，如图2 所示。变量变化空间是一个N维空间，其坐标轴是各不确定性变量的变化值。由目标及可行性空间映射至变量变化空间的集合称为灵敏度区域，可以表示为

图1 可接受目标变化区域（AOVR）

图2 可接受约束变化区域（ACVR）

其中，Sf是目标灵敏度集合，Sg为可行性灵敏度集合，可由式具体表示：

其中，Δfm是第m 个目标对应的预置AOVR。集合Sf为满足M 个目标稳健性条件的所有Δx的集合，Sg为满足G 个可行性稳健性约束的所有Δx的集合。

对于一组不确定性变量(x1，x2)，其灵敏度区域如图3中的不规则阴影部分所示。

图3 不确定性变量空间灵敏度区域

通过将AOVR 及ACVR 映射至参数空间，可以获取已存在设计方案的灵敏度区域，当存在多维度不确定性参数时，灵敏度区域可以为一个不规则空间体。在此基础上，需要进一步在灵敏度区域内获得一个规则矩形或超立方矩形作为参数的容差区间，如图3 虚线矩形框所示，为生产过程提供允许的最大加工误差。

3 基于“逆向设计”思维的稳健性分析方法

为了根据设计者对产品性能的要求获得容许的最大加工误差，本文提出基于“逆向设计”思维的稳健性分析方法，从目标及约束的容许变化范围出发，反向求得不确定性变量的最大容差区间。

对于一个预选设计方案(x0，f0)，包含具有不确定性的变量x0（x0=(x1，x2，…，xN)）以及最优的目标值f0（f0=(f0，1，…，f0，M)）。这里所说的预选设计方案是指被确定用于制造过程的设计，或者是由概念设计阶段产生的确定性设计方案。由于不确定性因素的影响，x0会出现一定程度的波动并影响实际的产品性能。

将目标稳健性要求与可行性稳健性要求均看作稳健性约束，则式（1）描述的区间不确定性下的产品设计问题可以表述为

其中，Ri包含M 个目标稳健性约束和G 个可行性稳健性约束，如式（5）所示：

式中，Δfi为第i 个目标对应的AOVR 值，在实际工程问题中，可能代表产品性能或质量要求。在此基础上，求取最大的参数容许变化，如实际加工中允许的最大加工误差，进而通过选择合适的设备或制造手段控制加工精度以保证产品实际性能。

本方法采取内外双层嵌套的结构求取不确定性参数的最大容差区间：1）外循环用于搜索不确定性参数的最大区间；2）内循环计算最坏可能情况变化（worst-case variations，WCV），并以此来验证搜索过程中的各区间是否满足稳健性要求。

所提出方法的结构框图如图4 所示。由于许多工程问题需要得到上下偏差相等的对称容差区间，本文选择关于原点对称的区间为求解目标，外循环目标设定为区间长度。首先经过预处理得到初始阈值，即确定初始的参数变化上界Δxmax及下界Δxmin。在初始阈值[Δxmin，Δxmax]内，由外循环随机生成不确定性区间值Δxl，并将其传递至内循环，由内循环在[- |Δxl|，| Δxl|]内搜索对应的WCV值；为减少计算成本，搜索WCV时引入支持向量机SVM分类模型，代替目标或约束值的计算过程。根据所得的WCV 判断不确定性参数值在每个区间变动时是否均满足目标稳健性及可行性稳健性，若不满足，则将对应的WCV 值作为惩罚项添加至外循环的搜索目标中；最后在外循环搜索获得最大的参数容差区间。

图4 基于“逆向设计”思维的稳健性分析框架

该方法的具体实施步骤如下：

步骤1：试验设计与SVM分类模型构建

采用拉丁超立方采样生成一组i×nx维训练集样本点u，其中i 是训练集样本点的个数，nx 为不确定性变量个数。根据max(R(u))的值对样本点分配标签，即对max(R(u))≤0 给定分类标签w=-1，反之，w=1。通过(uw(u))构建SVM 分类模型，判断在不确定性波动下，预选设计方案的目标及约束是否均满足稳健性要求。

步骤2：初始化参数变化阈值

在具体工程问题中，初始阈值可以为加工设备的最低加工精度，可表述为[Δxmin，Δxmax]。

步骤3：在外循环中生成区间值

根据外循环目标F，通过遗传算法搜索最大的区间值。首先需在外循环随机生成初始种群，即区间值Δxl，对任一Δxl有Δxmin≤Δxl≤Δxmax。然后将区间值Δxl传递至内循环。

步骤4：求解内循环

对外循环传入的每个区间值Δxl，在内循环中，搜索各区间值Δxl对应的WCV，其中，目标及约束值由SVM 分类模型的标签值确定，式（6）给出了WCV的求解表达式。

其中，Δx为[-|Δxl|，|Δxl|]内的变量值。

步骤5：判断稳健性

若WCV＞0，说明对应的区间可能存在部分区域不满足目标稳健性或可行性稳健性要求，则跳出搜索，将该WCV值传回外循环，并作为惩罚项添加至外循环目标中；若最终搜索得到的WCV＜0，则说明该区间被参数灵敏度区域完全覆盖，即区间内的参数变化始终满足稳健性约束，令这样的WCV 值为0并返回外循环。外循环目标中，WCV的添加方式如式（7）所示：

其中，P为惩罚因子。

返回步骤3 直至遗传算法达到设定的最大遗传代数。

步骤6：输出不确定性参数的最大稳健区间

最终搜索得到满足稳健性要求的不确定性参数最大容差区间：[- |Δxl|，| Δxl|]。

4 声学超材料几何参数的容差设计

微结构的设计是声学超材料器件设计中的关键步骤，它对超材料器件的可实现性及水声调控能力都有着重要的影响，而微结构的加工精度也对超材料器件的声学及力学性能有重要影响。文献［16］设计了图5 所示的铝基声学超材料设备，并对各参数进行了分析，不同的参数类型对微结构的体积模量与质量密度会产生不同程度的影响，例如六边形连接杆的长宽比增大，将可能导致各单胞部分无法按预期设计控制所有入射声波能量。

图5 铝基声学超材料构件［16］

本文针对图6 所示钛基声学超材料微结构，图中上半部分为声学超表面，下半部分为刚性墙，根据设计要求的声学性能进行稳健性分析。声学超表面由周期性的六边形单胞构成，每个六边形单胞边长L=24mm，在x 和y 方向上分别排列H 和V 个单胞时超表面的长度及厚度分别为

图6 声学超材料微结构

其中，Δx为装置整体长度，l 为其厚度；在x 方向有43 个单胞即H=43；在y 方向单胞数为3 即V=3。由于离散性，所设计微结构长度略长于预设尺寸。

在声学超材料微结构设计中，主要包括图7 所示t、m、b、r四类参数，其中t为单胞六边形连接杆厚度，m为质量块顶点四边形高度，b为质量块四边形宽度的一半，r为三角形顶点到四边形距离。

图7 六边形单胞最小重复单元

由于声学超材料多应用于制造隐身斗篷等，制造企业及其客户较关心产品的声学性能，要达到“隐身”效果，需要尽可能降低其散射强度，所以设定优化模型的目标为微结构的远场散射系数。该声学超材料微结构在2.5kHz～5kHz 具有较好的波控性，选择频率为2.5kHz、3kHz、4kHz 及5kHz 情况下的远场声散射系数的平均值为目标。根据图7所示几何关系，各单元中的四类参数还需满足一定约束使附加质量块的整体高度小于六边形单胞边长。优化模型如式（9）所示。

其中，f1～f4分别对应上述四种频率环境下的远场声散射系数；半侧22 组t、m、b、r为输入的不确定性参数，即t、m、b、r为包含22个元素的向量。

对该微结构，存在一组预选设计，即经设计确定的用于制造过程的设计方案，其中预选设计变量如表1 所示，预选目标值f0=92.93 为预选设计变量下的声散射系数平均值。要求声学性能不超过(1+1%)f0，式给出目标可接受变化范围，

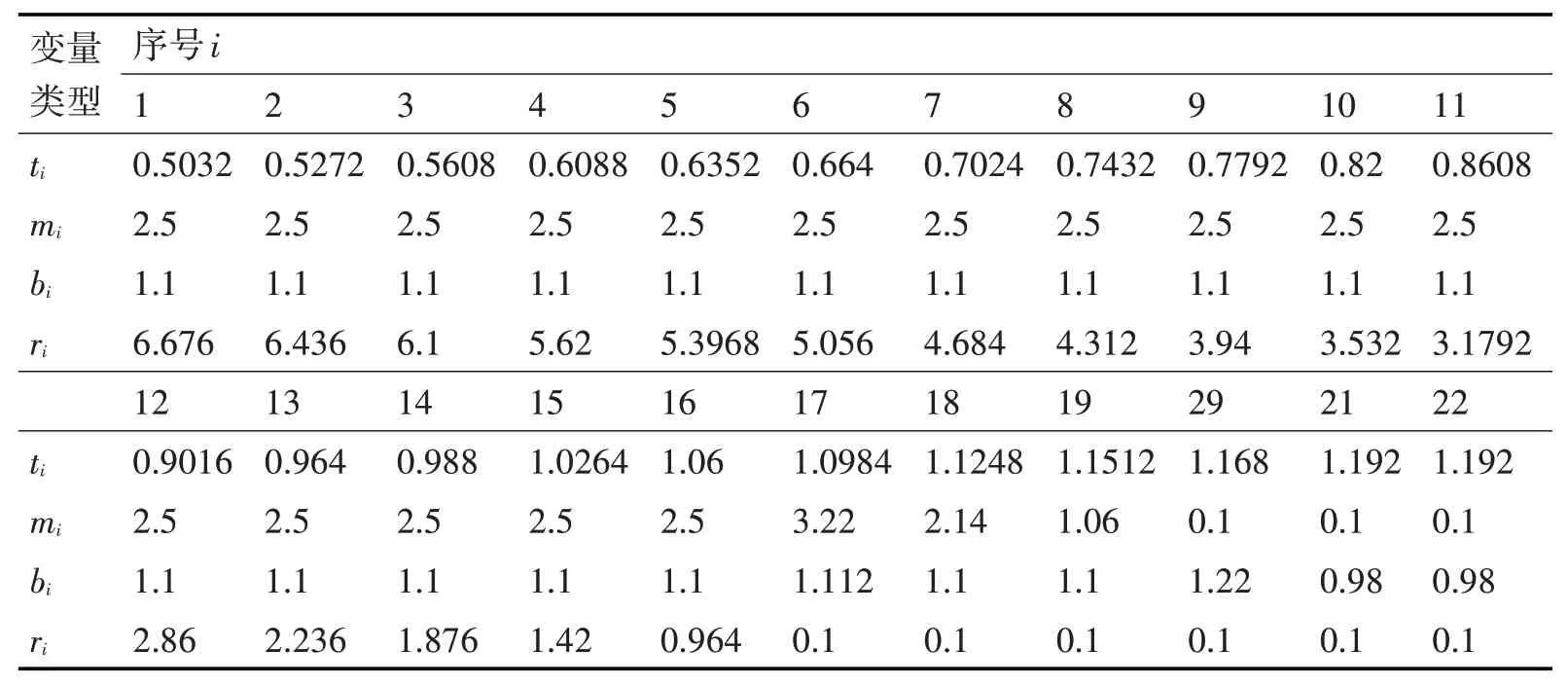
表1 预选设计变量

其中，x0=(t0，m0，b0，r0)，Δx为区间不确定性变化。根据加工条件，给出Δx的初始阈值为[-0.15，0.15]。

由声学性能要求与几何尺寸约束可知，该问题的稳健性约束如式（11）所示：

式中，R1为目标稳健性约束，R2为可行性稳健性约束。根据给定的设计性能要求，分析远场散射系数与各最小单元的不确定性参数之间的关系，获取性能要求下不确定性参数的容差区间，即实际加工过程允许的最大加工误差。

利用COMSOL Multiphysics 的声固耦合模块对该微结构声散射特征进行模拟，在预选设计变量下，可得到不同频率下的散射声压。选用模量为108GPa，泊松比为0.34，密度为4500kg/m3的钛为基材；六边形单胞质量密度为ρ=1000kg/m3，杨氏模量E=10MPa，泊松比v=0.475。由于主要应用于水下装备，计算远场声压级时使用水的参考压力，设定声速Cb=1500m/s。

在式（10）给出的声学性能要求下，通过基于“逆向设计”思维的稳健性分析，获取不确定性参数t、m、b、r 的容差区间。考虑COMSOL 的仿真成本（单次仿真耗时30min～60min），引入支持向量机SVM分类模型，用以进行内循环最坏可能情况分析中的目标稳健性的判断。

SVM 分类模型构建的具体实施过程为：1）通过拉丁超立方采样，在区间[x0-0.15，x0+0.15]内生成200 组样本点u；2）对样本点u，利用COMSOL 仿真得到相应的输出响应值f(u)；3）若响应值满足式目标稳健性要求，给定其分类标签w(u)=-1，反之，给定分类标签w(u)=1；4）利用[uf(u)]训练SVM 分类模型，后续可用于判断未经试验的不确定性设计是否满足所有的目标稳健性约束；5）采用K 折叠交叉验证评价SVM 模型的分类准确度，将[uf(u)]均分为K 组，用其中(K-1)组子集数据训练SVM 分类模型，并用训练出的模型对其余一组子集数据进行分类，通过与仿真结果对比验证模型分类准确度，依次得到K个模型的分类准确度，取其平均值作为SVM 分类模型准确度的评价指标。经验证，当K=10 时SVM 模型的分类准确度为96%。

根据给定的初始阈值[Δxmin，Δxmax]=[-0.15，0.15]，在外循环中由遗传算法生成初始种群，即随机区间值Δxl，并传入内循环。在内循环中搜索区间内的WCV值，WCV具体表达式如式（12）所示：

式中，R包括目标稳健性约束（式（11）R1）与可行性稳健性约束（式（11）R2），其中，目标稳健性约束通过SVM分类模型给出的分类标签w( Δx)表示。

将WCV 传回外循环，在外循环中进行稳健性判断。经过内外双层嵌套结构搜索，最终可得最大的容差区间为：[-0.1，0.1]。

使用Monte Carlo 法验证该区间稳健性。在区间[-0.1，0.1]内随机生成50 组Δx，将(x0+Δx)代入模型中，经过COMSOL 仿真输出对应响应值，目标稳健性验证结果如图8 所示。同时根据式（11）中的R2验证可行性稳健性，验证结果如图9所示。

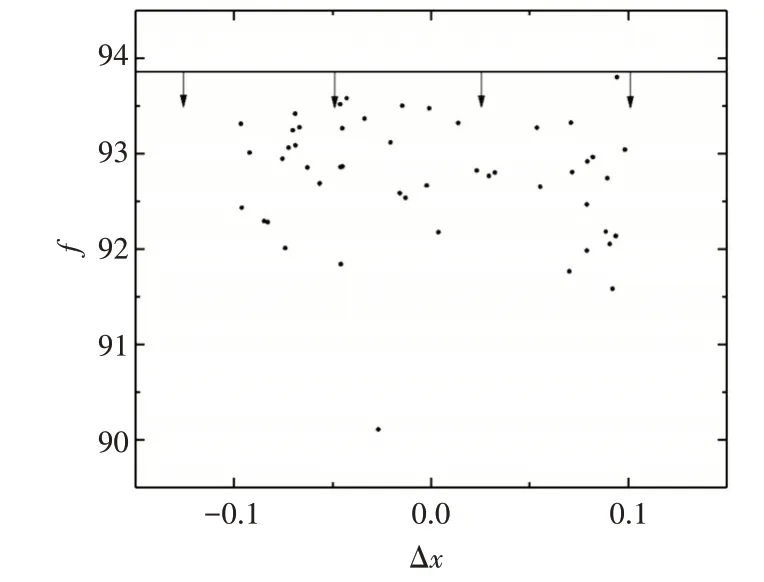
图8 声学超材料目标稳健性验证

图9 声学超材料可行性稳健性验证

为证明所得区间为最大容差区间，对于区间[-0.1，0.1]，对应得到WCV=-1.2160×10-5＜0 ；将该区间扩大0.05%，并进行最坏可能情况搜索，得WCV=3.7834×10-5＞0。则可认为，基于“逆向设计”思维的稳健性分析方法得到微结构参数容差区间[-0.1，0.1]为容许条件下的最大区间。

5 结语

本文针对声学超材料制备过程中的加工不确定性问题，采用基于“逆向设计”思维的稳健性分析方法，根据设计者提出的性能要求，反向获得不确定性参数的最大容差区间。根据上文研究内容，可得到以下结论：

1）本文提出了基于“逆向设计”思维的稳健性分析方法，通过将目标稳健性和可行性稳健性要求转化为不确定性参数的灵敏度区域，建立不确定性参数波动与性能变化之间的关系，并进行稳健性判断，最终获得不确定性参数的最大容差区间。

2）针对具体的声学超材料微结构设计，应用所提出的方法，根据微结构声学性能要求和几何关系约束，获得不确定性参数的最大容差区间，即允许的最大加工误差。采用Monte Carlo 法验证该区间稳健性，结果显示不确定性参数在所得容差区间内变动时不会违背目标稳健性及可行性稳健性要求；结合最坏可能情况分析证明，所获得的区间为允许条件下的最大区间。

3）根据获取的不确定性参数最大容差区间可以确定允许的最大加工误差，在保证性能的同时，能最大限度放宽加工精度要求，降低制造成本。