一种新的多姿态人脸图像识别方法*

徐胜超

（广州华商学院数据科学学院 广州 511300）

1 引言

目前应用较为广泛的生物识别技术通常是语音识别技术和人脸识别技术，尤其是人脸识别技术，最近几年以来成为专家讨论的热点话题。现阶段人脸识别技术中，多姿态人脸识别技术仍处于研究初始阶段，是一项极其复杂的技术。多姿态人脸识别是指对人脸特定的多种生理特征进行辨别的一种技术［1～2］，广泛应用在各个领域。其目的是保护隐私，去除人脸特征中肉眼可辨认的固定的信息，由于它具有隐私保护功能，所以要对其进行识别的因素较多。多姿态人脸识别过程中需要去除能确定前景身份的信息，根据剩余信息判断前景动作，进而进行身份识别。

对于多姿态人脸识别，相关学者进行大量研究。例如文献［3］考虑深度学习，利用轻量级和多姿态联合，在MTCNN 算法（Multitask cascaded convolutional neural network，多任务级联卷积神经算法）下进行人脸检测，最终实现人脸识别。文献［4］通过长短期记忆网络寻找人脸关键点，并且将其设定为人脸朝向描述子，动态更新描述子的变化情况。使用增加聚类方法对人体头部信息进行聚类处理，完成人脸识别。文献［5］研究优化相关人脸识别方法，考虑依恋取向，提出识别人脸面部情绪的优化方法，记录了焦虑组和回避组的事件相关电位。回避型依恋的人在愤怒测试中更准确，而焦虑型依恋的人在快乐测试中更准确。文献［6］提出基于遗传特征结合的算术编码局部二值模式人脸识别，局部二值模式是利用人脸识别算法收集局部特征的尝试之一。提出的方法是算法编码LBP（Local Binary Pattern，局部二进制模式），在LBP计算过程中使用算术编码过程，而不是使用原始阈值。文献［7］提出面向人脸识别的归一化Gabor 特征的局部侧面流形。由于多尺度卷积和小波的方向性，投影特征在维数上是实质性的。当在实际人脸识别中使用这些特征时，将需要相对较长的分类过程。通过使用称为局部线性嵌入的流形学习方法，同时横向和局部地减小Gabor 特征的大小来解决这个问题。因此，该方法被表示为局部横向归一化局部Gabor特征向量。

由于上述方法未能对人脸图像进行去噪处理，导致出现多姿态人脸结果不准确，识别时间增加的问题。为了解决上述问题，本文提出一种新的多姿态人脸图像识别方法，我们的方法创新性是根据结合局部奇异值特性的相关原理作为思路，获取约束条件的阈值，最后通过实验验证了本文方法的实际应用效果。

2 多姿态人脸识别方法的预处理

2.1 人脸图像去噪处理

因为受人体自身以及外界干扰等因素的影响，使多姿态人脸特征提取具有很大的随机性，识别方法需要具备合理的控制评估能力，人脸图像去噪处理能够对人脸特征进行刻意隐藏和控制评估，而传统的控制系统通常依靠专家经验的方法来完成人脸特征识别，不能有效地处理掉身份后不断变化的不确定性干扰因素，因此无法完成该功能。对于人脸图像去噪处理过程的随机变化，通常不能用精确的数据模型来描述。该问题通过小波变换技术解决，通过对去除身份后的人脸图像特征和改变面部特征进行区分，然后判断彼此的关联性，并根据上述两项输入获得网络的输出，即人脸图像去噪处理后的变化程度，对于相应的中间转化部分以及特征迁移部分分析，从而获得去噪处理的输出结果。

小波变换能够精准描述不同目标对象的全部细节信息，对人脸图像进行小波交换，再由小波变换得到小波系数，通过小波系数综合反映出人脸图像的特征。二进制小波变换是人脸图像预处理中常用的方法，是指连续小波变换半离散化状态的一种结果，对不同的幂级数具有优先性特征［8］。由分析处理结果可知，当幂指数持续增加时，会引发比较明显的变化，因此对二进制小波变换的分析可以起到较好的效果。

当人脸图像信号如果需要进行二维小波变换时，就必须对不同方向的滤波器进行处理，分别获取不同子带图像。其中人脸图像进行一层小波变换的结果，如图1所示。

图1 人脸图像一层小波变换示意图

由图1 可知，LL、HL、LH、HH 均代表小波交换参数。通过小波包能够对人脸图像的高频部分进行详细的描述和分析［9～10］，人脸图像一层小波变换具有较强的信息分析能力。

以下详细给出通过小波包对人脸图像进行去噪的具体操作步骤［11～12］，如图2所示。

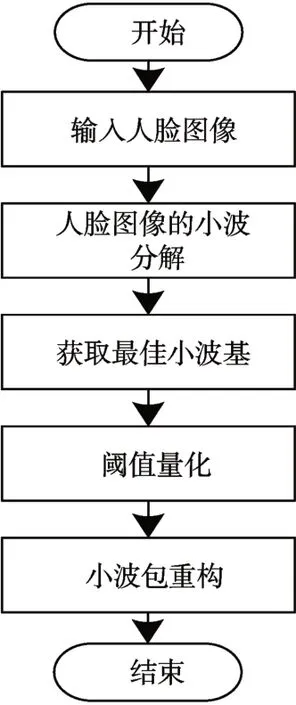
图2 基于小波包的人脸图像去噪流程图

1）人脸图像的小波分解：输入人脸图像，在图像中随机选取小波包特征值，确认分解层［13～14］。

2）计算人脸图像识别最佳树，根据计算结构得到最佳小波基：结合已经给定的熵准则进行计算，获取最佳树。

3）小波分解系数的阈值量化：在最佳树的基础上，选择已经满足结合局部奇异值特性约束条件的阈值，同时量化处理人脸图像的高频系数。

4）小波包重构：重构多姿态人脸图像的高低频系数，得到全新的阈值，实现人脸图像去噪。在此基础上，结合局部奇异值特性，继续多姿态人脸识别的后续步骤。

2.2 结合局部奇异值特性的多姿态人脸识别

因为多姿态人脸图像通常都是是动态的［15～16］，所以在原始位置上计算出位移的变化，然后将采集的人脸动态位移作为后续位置特征输出的初始值，通过反复的计算，得到准确的人脸自适应阈值。由于人脸自适应阈值受到时间序列的影响，多姿态人脸的特征点会发生相应的位移，此时需要依据多姿态人脸图像中任意像素点的像素值向量Hab，建立时间序列模型MXC：

式（1）中，Dur(·) 表示曲线拟合函数，完成多姿态人脸图像帧数归一化处理。将根据结合局部奇异值特性的相关原理作为指导思想，获取人脸自适应阈值。采用下列的表达形式，确定自适应阈值向量的取值范围，使得：

式（2）中，Rfdf表示动态序列中未识别的人脸姿态特征点，Bdd表示在预设人脸图像中对应特征点［17］，然后在待检测图像中确定表情定位点的位置，通过公式可表示为

式（3）中，Xjf表示确定多姿态人脸识别定位点横坐标，Ydf表示确定多姿态人脸识别定位点纵坐标，T表示转置。根据获取到的多姿态人脸定位点信息［18］，利用结合局部奇异值特性进行多次运算得到多姿态人脸的梯度矩阵FGB，确定多姿态人脸图像中的自适应阈值［19～20］，具体公式如下：

式（4）中，λ表示多姿态人脸图像中的不匹配向量，同时使用式（3）与式（4）进行反复运算，得到最终的自适应阈值。使用上述计算过程对采集到的位移特征点展开计算，确定多姿态人脸的动态特征，完成多姿态人脸识别。

3 仿真实验与性能分析

为了验证本文所方法的效果及综合有效性，根据所提出方法进行实验，实验所需图像主要从CMU Multi-PIE人脸数据库选取［21］。

以下实验测试对比三种不同方法的误识率，在人脸识别的过程中，需要将测试使用的人脸图像和训练样本相同的部分进行统一处理，提取局部和整体的特征向量，误识率具体的计算公式如下：

式（5）中，‖x‖1代表混合向量的绝对值。利用三种不同方法通过上述公式进行误码率对比，结果如表1所示。

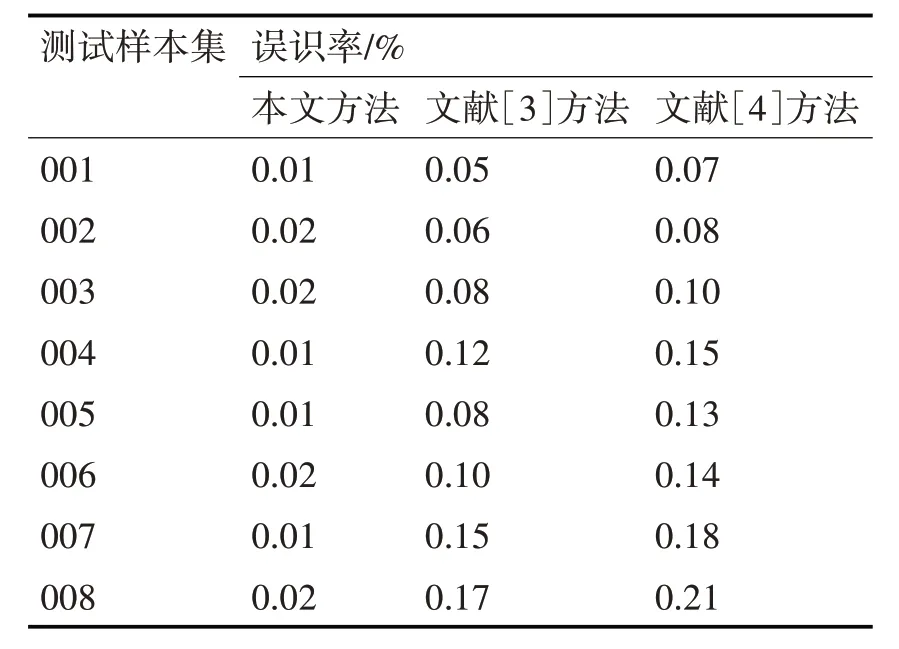
表1 误识率测试结果分析

分析表1 中的实验数据可知，本文方法的误识率在三种方法中为最低，其原因是本文方法在未进行人脸识别前，采用小波包对人脸图像进行去噪处理，一定程度上可以提高识别结果的准确性。

实验选取3 幅不同的人脸图像作为测试对象，原图像如图3所示。

图3 算法测试原始图像

分别采用本文方法、文献［3］方法、文献［4］方法进行性能识别，具体的实验测试步骤如下：

步骤一：首先预处理人脸图像，主要使用分类器获取所需人脸图像信息，建立人脸-姿态目标矩阵。

步骤二：计算目标矩阵邻域间最佳识别目标的相似性，且依据目标对多姿态人脸图像的契合程度规划相近的邻域集。

步骤三：建立多姿态人脸图像识别信息模型，实现识别性能选取，不同方法性能对比结果如图4所示。

图4 不同方法的多姿态人脸识别性能测试结果

分析图4 中实验数据可知，本文方法能够精准识别出人脸的不同姿态信息，而另外两种方法只能够识别局部信息，充分证明本文方法能够获取高准确性的识别结果。

人脸图像被遮挡也会影响人脸识别结果的准确性，以下实验测试重点分析在人脸遮挡面积不断上升情况下各个方法的人脸识别率，具体实验结果如图5所示。

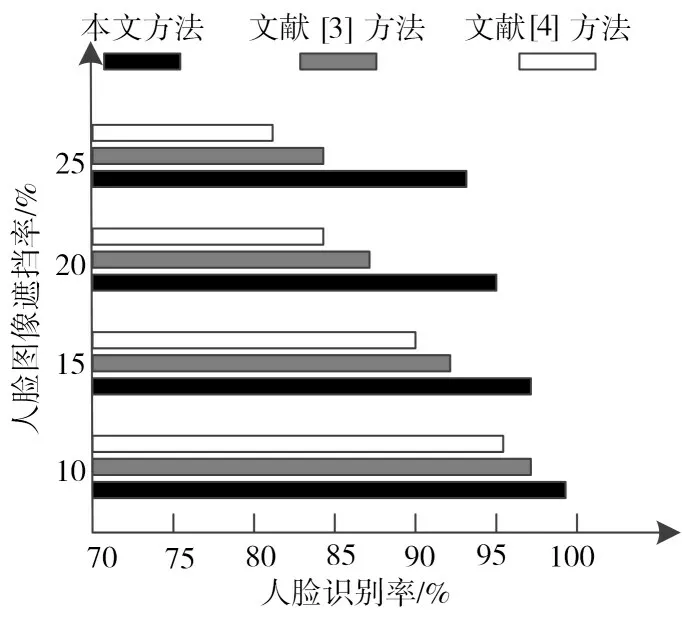
图5 不同遮挡率下人脸识别率测试结果

分析图5 中的实验数据可知，随着人脸被遮挡部分持续增加，各个方法的人脸识别率也开始发生变化。与文献［3］方法和文献［4］相比，本文方法能够精准识别不同的人脸姿态信息，充分证明所提方法的优越性。

由于不同方法的操作流程不同，导致各个方法进行人脸识别的时间也存在比较明显的差异，以下实验测试将人脸识别时间作为测试指标，详细的实验对比结果如6所示。

由图6 中的实验数据分析，相比文献［3］方法和文献［4］，本文的人脸识别用时较短，速度明显更快，同时更证实所提方法能够以更快的速度完成人脸识别，相同数据识别量情况下的不同方法所用的不同识别时间可准确反映识别效率的高低，识别效率是概括人看识别可靠性的重要指标之一。

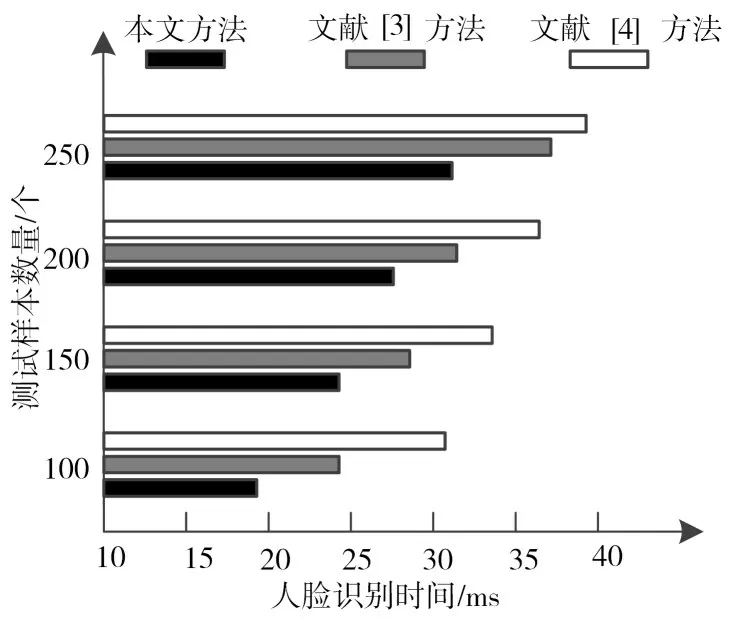
图6 人脸识别时间序列测试结果

4 结语

通过上述研究得到如下结论：1）本文多姿态人脸识别方法的误识率平均为0.015；2）能够精准识别出不同姿态信息，且识别率较高；3）本文提出方法识别时间较短，具有较好的效果。

由于研究时间有限，本文方法仍然存在不足，后续将对其展开更加深入地研究：1）未来可以加强多姿态人脸图像预处理工作，为获取更好的识别结果做准备。2）需要深入研究人脸图像微表情识，避免微表情识别混淆问题，下一步工作重点可以就加强对人脸表情进行深入研究。