基于改进Douglas-Peucker 的自适应阈值渔船轨迹数据压缩方法*
段浩然 刘明剑 朱云鹤 张思佳
(1.大连海洋大学信息工程学院 大连 116023)(2.设施渔业教育部重点实验室 大连 116023)
1 引言
据农业部2021 年末统计,我国现有渔船52.08万艘,从事渔业的人口为1634.24万人,全国渔业经济总生产值约为29689.73亿元,其中海洋渔业捕捞经济生产值占比较重,约为2303.72 亿元[1]。我国是渔业大国,渔业捕捞为沿海地区的发展做出了重要贡献。为了保证渔船捕捞作业的安全性和合法性,保护海洋生态平衡实现渔业的可持续发展,有必要对渔船行为进行监督与管理[2]。
船舶自动识别系统(Automatic Identification System,AIS)是强制在渔船、货船和客船等船舶上安装的助航仪器[3],能自主地、不断地向外播发和接收船舶的呼号、船名等静态信息和航向、航速等动态信息,目的在于识别和跟踪船舶行驶轨迹[4]。因此通过对渔船的AIS 数据进行分析是监管渔船行为、探明渔船的捕捞方式、作业状态以及捕鱼热点等深层次信息的有效方式之一[5~7]。渔船出海作业时间较长,横跨区域广[8],长时间长距离的航行产生了大量的AIS 数据[9],同时也会加剧数据存储分析的任务量和系统的负荷[10],因此需要有效的轨迹压缩算法处理海量的AIS数据。
轨迹压缩算法是在减少轨迹点的同时设定压缩条件,保障轨迹特征信息损失最少。对相同轨迹设置不同的压缩条件,压缩后的轨迹会存在较大的差异,因此需要对轨迹压缩算法中压缩阈值进行合理设置。
Douglas[11]等提出Douglas-Peucker 算法,根据设置固定的压缩阈值对轨迹进行简化,但不适用于所有类型的轨迹。大部分学者在该算法基础上进行改进,张树凯等[12]基于DP 算法为多个实验选择了不同的阈值,该方法以航行船舶的船舶域为阈值,即船舶长度的0.8 倍。赵梁滨等[13]将合适阈值设置为船舶长度的0.5 倍~1 倍。岛屿附近海域的适当比例通常为船舶长度的0.1 倍~10 倍。高淼等[14]将距离阈值设定为[30,300]m,将回旋和漂移的角度阈值设定为[1°,9°]。此外,给出了高、中、低水平的距离阈值,分别为船舶长度的43%、38%和33%。魏赵坤等[15]将滑动窗口算法、船舶导航角度偏差、位置偏差和AIS 的时空特征结合起来,距离阈值分别为船宽的0.731倍和1.274倍,航行角度偏差阈值是3.8°和5°。此外刘敬贤等[16]还提出了一种DP 算法和滑动窗口算法结合的轨迹简化算法。将DP算法的阈值设置为船舶长度的0.8倍,滑动窗口算法的阈值系数设置为1.6。
综上所述,轨迹压缩阈值设置主要有两种方式。1)经验阈值;2)船舶长度或宽度的倍数。然而,经验阈值容易受到水域的限制,难于确定测试范围以外水域的阈值。对于基于船舶长度或宽度设置的阈值,在大量异常静态信息的影响下会有误差。为了克服这些算法在阈值设置方面的不足,迫切需要一种自适应轨迹压缩算法,其阈值设置不再根据经验或船舶静态信息进行设定。
本研究针对上述问题,在DP 算法的基础上提出了ADP 自适应阈值压缩方法。首先,选择航向状态属性筛选轨迹点;其次,拟合所有子轨迹段的最大临界阈值集的曲线;最后,根据曲线中阈值变化不大且方向在垂直和水平上变化的特点,利用相邻点间的角度变化率设置自适应阈值。
2 相关定义
2.1 渔船AIS轨迹数据特点
由经度、纬度、时间等信息组成的轨迹点集合,被称为船舶的AIS轨迹。
相比于定班定线航行的商船和客船,渔船的轨迹数据有以下几种特点:
1)部分AIS 数据不准确。如表1 所示,船舶运动状态对数据的采集会产生一定影响,运动状态不同其上传数据的时间间隔也有所不同,将导致数据在传送和接收的过程中缺失[17],部分渔船由人工输入状态信息,存在操作失误的情况。

表1 AIS数据上传时间间隔
2)特征点数量多且密集。渔船在作业区内来回低速拖拽捕捞,频繁的转弯和掉头,这将导致产生了大量且密集的轨迹数据。图1[18]为船讯网中一渔船前往作业区捕捞的航行特征。
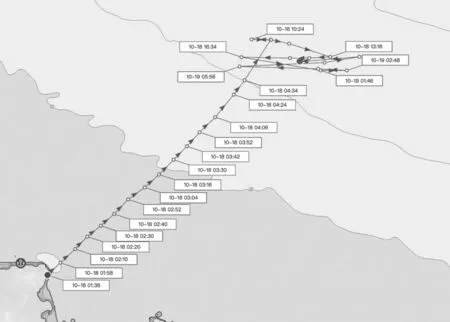
图1 渔船捕捞时航行特征
3)轨迹长且曲折。由于海面的环境复杂多变以及不固定的航线,渔船在捕捞作业后的轨迹点更随机。
2.2 相关定义与公式
定义1轨迹点:船舶的位置点用p表示,是一个三维的的轨迹数据,属性分别为经度、纬度、时间,表达式为
定义2原始轨迹:一连串随着时间前后顺序的原始轨迹点组成的集合,用T表示,其表达式为
定义3压缩轨迹:对原始轨迹进行压缩处理,筛选轨迹点后,按照时间前后顺序组成的新轨迹集合,用Tc表示,即
定义4轨迹段:在原始轨迹T或简化轨迹Tc中,将pi和pj连接组成的线段,用表示。
定义5特征点:若某点处的航向角差值和距离差值大于对应的航向角阈值和距离阈值,则称该点为特征点。
定义6压缩率:指丢弃的轨迹点数量与原始轨迹点数量的比率。单个轨迹(表示为SCR)的压缩率为
式中n是轨迹点的总数,m是丢弃轨迹点的数量。
定义7点的临界阈值ξ:如果距离阈值仅使轨迹点a在压缩后成为特征点,则该阈值称为点a的临界阈值,记录为ξ。
定义8经纬度坐标转换:将地理坐标转换为墨卡托投影中的坐标来提升精度。假设未转换轨迹点的经纬度坐标为(φ,ω),转换为墨卡托投影的坐标为(x,y),则转换公式如下:
式中,r0为基准纬度圈的半径;a为地球的长轴半径。
式中,e为地球的第一偏心率;q为等距纬度。
在式(3)中,Tc为同步欧氏距离(Squared Euclid Distance,SED)。表示为原始轨迹中的点在压缩轨迹中按照时间比例对应的欧氏距离。假设原始轨迹中的某一点为p=(xi,yi,ti),压缩轨迹中的某一点为则p'的坐标计算公式为
所有轨迹的平均SED 表示为AASED(All Average Squared Euclid Distance),其中N为船舶轨迹总数:
定义9角度变化率r:指拟合曲线中两个相邻点在切线方向上的变化率。
3 相关算法及算法设计
3.1 DP算法
DP 算法的基本原理是保留原始轨迹的首尾两点并相连接做基线,依次计算该轨迹上所有点到基线的欧式距离,并找出距离最大的轨迹点,将其距离值与设定的距离阈值进行比较,小于距离阈值,则舍弃这条直线上的点,大于距离阈值,则保留该点。将原始轨迹从该点处分成两段,得到两条子轨迹段并对子轨迹段重复上述步骤,迭代计算,直到所有轨迹点到对应基线的距离都小于距离阈值或轨迹内只剩余首尾两轨迹点。
如图2 所示,设置距离阈值ε,原始轨迹为。DP 算法先将起点和终点连接得到轨迹段并代替原始轨迹,分别计算所有轨迹点p1,p2,p3,p4,p5,p6到的欧氏距离,p3点距离最远,且dmax(P3) >ε,保留p3点,再次递归处理轨迹段,直到对应轨迹段的最大欧式距离小于给定的距离阈值ε,最终得出简化轨迹为Tc={p0,p3,,p5,p7} 。
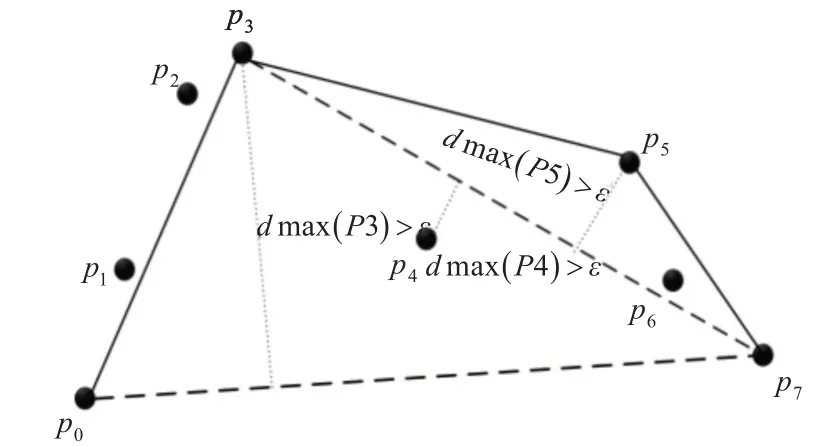
图2 DP算法
3.2 ADP自适应阈值压缩方法
本研究在DP 算法基础上提出的ADP 自适应阈值压缩方法是为了能自适应进行阈值压缩。解决以往方法中阈值设置基于经验,导致应用受限,以及阈值设置基于船舶静态信息,由于信息不正确而导致压缩效果差甚至不成功的问题。
渔船轨迹数据中属性较多,但渔船在作业时会在某区域内低速行驶并存在多次转向、掉头的情况。故本研究在算法中使用航向状态属性,利用相邻轨迹点之间的航向变化状态信息过滤非转折点。在初步保留转折点之后,对小于距离阈值的轨迹点进一步压缩提取特征点,并同时计算所有子轨道段的最大临界阈值来检查阈值的临界点。最终达到对轨迹设置自适应阈值的目的。
3.2.1 非转折轨迹点过滤
渔船在捕捞时会在作业区域内低速拖拽并多次往返。针对渔船在作业时航向多变的特点,提出一种轨迹点过滤方法,通过轨迹点的航向变化过滤非转折点,筛选轨迹点。将航向变化小于角度阈值的点删除,大于角度阈值的点反应了渔船真实的运动情况,需要进行保留。
采用非轨迹点过滤方法,得出过滤率和角度阈值Δθ之间的关系,结果如表2 所示。当Δθ>10°时,过滤率的变化不显著。本文将角度阈值Δθ设为10°。

表2 过滤率与Δθ 的关系表
3.2.2 ADP算法基本步骤
1)输入原始轨迹点集T,航向角度阈值Δθ、距离阈值ε,通过滤除非转折点的方法,对航向变化差小于Δθ的点过滤,得到转折点集。
2)保留转折点集中的首轨迹点p0和末轨迹点p13并存储在集合Tc中,连接两点得到轨迹段,计算所有点到轨迹段的距离,得到距离最大值点p4以及ξ1,如果ξ1大于距离阈值,则p4点为特征点,保留该点存储在集合Tc中,将ξ1存储在集合Set(ξ)中,并以该点为界分为两个子轨迹段分是ST1,1和ST1,2。否则舍去这条轨迹上的点。
3)分别对两个子轨迹段ST1,1和ST1,2取最大距离值点p3和p9。比较两点到子轨迹段的距离,优先处理距离最大的子轨迹段。p9点到子轨迹段ST1,2的距离大于p3点到子轨迹段ST1,1的距离。如果p9点为特征点,则将p9点存储在集合Tc中,将该点到基线的距离ξ1,2存储在集合Set(ξ)中并以该点为界分为两个子轨迹段分别是ST2,1和ST2,2。
4)重复上述步骤,直到处理完所有子轨迹段。输出压缩轨迹集Tc以及所有子轨迹段的临界阈值集Set(ξ)。ADP算法如图3。
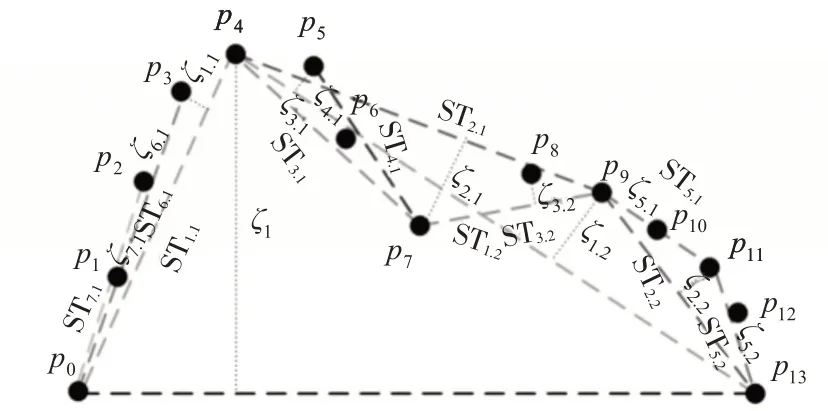
图3 ADP算法
为了能更直观地得出临界阈值之间的变化规律,对临界阈值集Set(ξ)进行拟合。

图4 子轨迹段临界阈值的分布(截取一部分)
函数拟合后得出a=321.32,b=0.03,c=1.22,d=0.11。将参数代入并画出曲线变化图,如图5 所示。
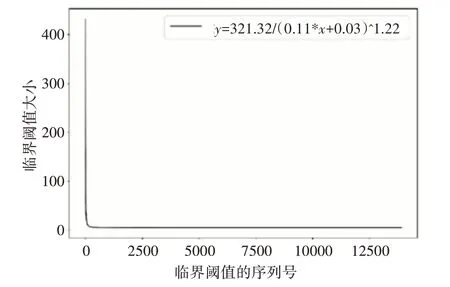
图5 子轨迹段临界阈值拟合结果
在数据库中随机选取两条轨迹T0和T17,做出拟合曲线并和图5 中的拟合曲线进行对比,如图6所示。
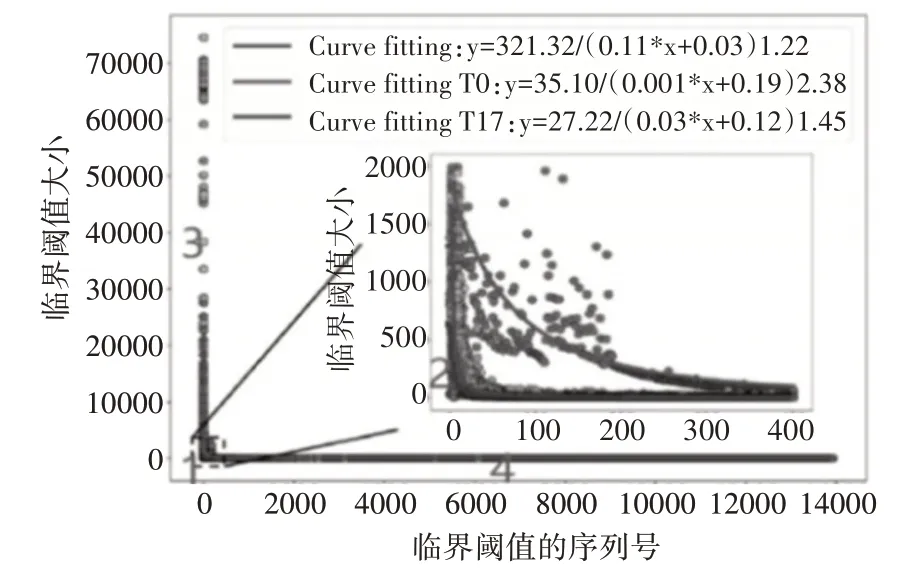
图6 多条轨迹的临界阈值拟合结果
图6 中三条拟合曲线的拟合优度R2计算公式如下:
式中,yi为真值,平均值为˙,拟合值为。三条曲线拟合优度分别为R2y=0.53,R2T0=0.70,R2T17=0.91。
如图6所示,区域3中的线是垂直的,虽然临界阈值变化迅速,但其方向变化不大;4 区的线是水平的,临界阈值变化不大,方向也几乎不变。从垂直方向到水平方向的变化主要发生在1 区。两个方向之间的转折点更能反映出曲线的特征,因此通过计算曲线中相邻点之间的最大角度变化率来设置最优阈值。
双曲线函数的导数计算公式如下:
第pi点和第pi+1点之间的角度变化率为
由上述公式可得,y曲线中x=3 时角度变化率最大,即y=55.6,最优阈值应设为55.6m,T0曲线中x=124 时角度变化率最大,即y=552.8,最优阈值为552.8m。T17曲线中x=25 时角度变化率最大,即y=33.3,最优阈值应设为33.3m。
4 验证试验
4.1 试验设计
为验证本文提出的自适应阈值渔船轨迹数据压缩方法的有效性,分别对单条渔船轨迹进行不同算法的压缩对比试验。算法采用Python语言编写,版本为3.7,IDE 采用PyCharm。轨迹数据以及试验数据集来源于“大连望海大数据信息有限公司”,渔船轨迹数据以.txt的文件格式存储。
4.2 试验结果
图7 中三种算法对渔船轨迹进行压缩处理后,原始轨迹点数目都较大幅度的减少,DP 算法虽能够保留轨迹的路径形状,但大量的特征信息被压缩,SW算法在轨迹点密集的区域出现失真,ADP算法压缩后的轨迹形态对于保留渔船的特征轨迹点和轨迹的形状特征有很大的帮助。

图7 渔船轨迹压缩前后效果对比图
算法对比结果如表3 所示,3 种算法的压缩率平均为99.5%(SW 算法),99.4%(DP 算法),98%(ADP 算法)。ADP 算法在保留了更多特征点的同时使得压缩后的轨迹与原始轨迹更相似。

表3 三种压缩算法试验结果
5 结语
针对现有轨迹压缩算法在设置距离阈值时存在采用基于经验设置最佳阈值的问题,在DP 算法的基础上提出了ADP 算法。实验表明,ADP 算法能够自适应设置阈值,不仅获得了较高的压缩效率,同时在保留轨迹特征的方面也有较大的优势,为渔船的行为分析提供更加精确的压缩轨迹。
然而,也有不足之处。没有考虑到船舶的航向和速度所带来的影响。因此在以后的工作中会着重考虑上述两种因素来改进压缩算法。

